端曲面齿轮副复合运动规律及受力分析

引用本文

林超, 刘毅, 魏艳群, 朱才朝. 端曲面齿轮副复合运动规律及受力分析. 2017, 47(1): 157-162
LIN Chao, LIU Yi, WEI Yan-qun, ZHU Cai-chao. Composite motion law and force condition of curve-face gear pair. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 157-162 复制到剪切板

Permissions

端曲面齿轮副复合运动规律及受力分析

林超, 刘毅, 魏艳群, 朱才朝

重庆大学机械传动国家重点实验室,重庆 400044

作者简介:林超(1958-),男,教授,博士.研究方向:新型齿轮传动.E-mail:linchao@cqu.edu.cn

基金:国家自然科学基金项目(51275537); 重庆市研究生科研创新项目(CYS15008).

摘要

根据微分几何和齿轮啮合原理的相关理论,分析了端曲面齿轮副复合运动的两种不同的传动形式,并采用仿真分析验证了其运动规律。计算并分析了端曲面齿轮副复合运动时的受力状况以及该齿轮副啮合过程中压力角的变化情况。搭建了验证其运动规律的试验平台,使用激光位移传感器测量该齿轮副的位移,将试验结果与理论值和仿真结果进行对比,验证了计算结果的正确性。

关键词: 机械设计; 复合运动; 端曲面齿轮; 受力分析

中图分类号:TH132.4 文献标志码:A 文章编号:1671-5497(2017)01-0157-06

Composite motion law and force condition of curve-face gear pair

LIN Chao, LIU Yi, WEI Yan-qun, ZHU Cai-chao

State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, China

Abstract

According to the theories of differential geometry and the gear engagement principle, this paper analyzes two kinds of composite transmission form of curve-face gear pair. The motion law is verified by ADAMS simulation. The force condition of the composite motion of the curve-face gear pair is analyzed and calculated, and the change state of the pressure angle of the gear pair is also obtained. An experiment platform is built to verify the motion law, and laser displacement sensor is used to measure the displacement of the gear pair. It is shown that the calculation results are in consistence with the theoretical analysis results and the simulation results, which validates the calculation method.

Keyword: mechanical design; composite motion; curve-face gear; force condition

Show Figures

0 引言

常见的组合机构有实现预定轨迹要求的联动凸轮组合机构、凸轮-连杆组合机构、实现任意停歇或复杂运动规律要求的凸轮-齿轮组合机构、实现多种运动规律及轨迹要求的齿轮-连杆组合机构和齿轮与液压的组合机构等^{[1, 2, 3, 4, 5, 6]}。这些机构能够实现特定要求的运动轨迹或复合运动, 但是结构较为复杂, 体积和重量比较大, 并不适用于结构尺寸受限、运动规律过于复杂的场合。

复合运动机构中独特且结构较为简单的一种是复合运动齿轮副, 它依靠齿轮副的节曲线形状变化实现旋转/直动复合运动。复合运动齿轮副包含正交复合运动锥齿轮副^[7]、正交复合运动端曲面齿轮副^[8]、复合运动面齿轮副^[9]、复合运动非圆齿轮副和非圆齿轮齿条运动副。其中端曲面齿轮复合运动机构是在端曲面齿轮基础上提出的结合了凸轮机构、齿轮机构和非圆齿轮机构特点的一种新型的齿轮传动^[10]。这种运动副相比传统的组合机构结构更简单、可靠性更高, 可以取代一些传统的组合机构, 对于装备轻量化、简化机械结构意义重大。缺点是现阶段设计难度高, 加工制造困难。针对端曲面齿轮的研究已经比较详尽, 而端曲面齿轮副复合运动的研究却比较少, 集中在齿面求解、运动规律的计算和应用方面^{[7, 10]}。

本文对端曲面齿轮副复合运动的运动规律进行了仿真和试验验证, 并计算了其啮合过程中的压力角和受力状况, 为其设计和应用提供进一步的指导。

1 运动规律

1.1 齿轮副传动模型

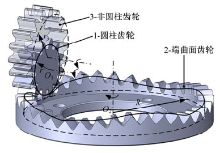
如图1所示, 齿轮1为普通直齿圆柱齿轮, 其节曲线半径为 $\begin{matrix} r; \end{matrix}$ 齿轮2为端曲面齿轮, 其节曲线半径为 $\begin{matrix} R; \end{matrix}$ 齿轮3为非圆柱齿轮, 其节曲线为二阶椭圆, 节曲线半径为r₃(θ ₃)。端曲面齿轮是一种用于相交轴间传递变传动比运动和动力的齿轮。端曲面齿轮的节曲线方程为:

$\begin{matrix} \{\begin{matrix} x_{2} = - Rcos θ_{2} \\ y_{2} = - Rsin θ_{2} \\ z_{2} = r_{3} (0) - r_{3} (θ_{3}) \end{matrix} \end{matrix}$ (1)

式中:θ ₂ 为端曲面齿轮的转角; θ ₃为非圆齿轮的转角。

	Figure Option View Download New Window
	图1 端曲面齿轮副复合运动传动系统模型Fig.1 Transmission model of composite motion of curve-face gear

当非圆柱齿轮3旋转轴固定并作为主动轮, 端曲面齿轮2作为从动轮, 其输出为变传动比的旋转运动, 此时即为端曲面齿轮副; 当以端曲面齿轮2作为主动轮, 圆柱齿轮1作为从动轮, 其输出为圆柱齿轮的旋转运动与圆柱齿轮的径向运动的复合运动; 当以圆柱齿轮1为主动轮, 以端曲面齿轮2为从动轮, 其输出为端曲面齿轮的旋转运动和端曲面齿轮的轴向移动的复合运动。通过修改端曲面齿轮的节曲线可以相应改变输出端的运动规律, 从而满足所要求的工作场合。本文以直齿圆柱齿轮1作为主动轮分析端曲面齿轮副复合运动的特性。

1.2 运动规律

当以直齿圆柱齿轮为主动轮时, 输出端轴向位移的运动规律为^[8]:

$\begin{matrix} s = z_{2} = r_{3} (0) - r_{3} (θ_{3}) \end{matrix}$ (2)

轴向移动速度变化规律为:

$\begin{matrix} v (θ_{2}) = \frac{d z_{2}}{d θ_{2}} = \frac{d z_{2}}{d θ_{3}} \frac{d θ_{3}}{d θ_{2}} \end{matrix}$ (3)

进一步求轴向移动加速度变化规律为:

$\begin{matrix} a (θ_{2}) = \frac{dv (θ_{2})}{d θ_{2}} = \frac{d (\frac{d z_{2}}{d θ_{3}} \frac{d θ_{3}}{d θ_{2}})}{d θ_{2}} \end{matrix}$ (4)

根据齿轮啮合原理, 齿轮啮合过程中啮合点的瞬时速度相等, 即 $\begin{matrix} {\vec{v}}_{1} = {\vec{v}}_{2}, {\vec{v}}_{1} 、 {\vec{v}}_{2} \end{matrix}$ 分别为圆柱齿轮、端曲面齿轮上啮合点的速度。对于从动轮(端曲面齿轮)有: $\begin{matrix} {\vec{v}}_{2} = {\vec{v}}_{t} + {\vec{v}}_{a}, \end{matrix}$ 对于主动轮(直齿圆柱齿轮)有: $\begin{matrix} {\vec{v}}_{1} = {\vec{r}}_{1} {\vec{ω}}_{1}, \end{matrix}$ 则端曲面齿轮切向速度 $\begin{matrix} v_{t} = \sqrt[]{v_{1}^{2} - v_{a}^{2}} 。 \end{matrix}$

另外 $\begin{matrix} {\vec{v}}_{t} = R {\vec{ω}}_{2}, \end{matrix}$ 故有:

$\begin{matrix} ω_{2} = \frac{v_{t}}{R} = \frac{\sqrt[]{v_{1}^{2} - v_{a}^{2}}}{R} \end{matrix}$ (5)

式中: $\begin{matrix} {\vec{v}}_{t} \end{matrix}$ 为切向速度; $\begin{matrix} {\vec{v}}_{a} \end{matrix}$ 为轴向速度。

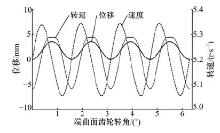
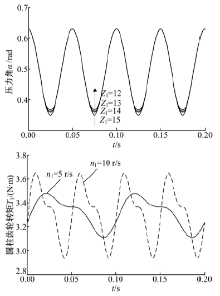
根据以上计算方法, 复合运动端曲面齿轮副采用如下参数时:圆柱齿轮齿数Z₁=12; 齿轮副模数m=2 mm; 端曲面齿轮齿数Z₂=36; 偏心率k=0.1; 节曲线半径R=35.91 mm; 端曲面齿轮阶数n₂=2; 主动轮转速N₁=150 r/min。可得端曲面齿轮副复合运动的运动规律如图2所示。

	Figure Option View Download New Window
	图2 端曲面齿轮副复合运动规律理论值Fig.2 Theoretical value of composite motion law of curve-face gear

从图2可以看出, 该端曲面齿轮副输出旋转/移动的复合运动, 而且端曲面齿轮的旋转和轴向移动规律均呈现出一定周期性, 当轴向运动的位移最大时, 轴向运动速度为零, 端曲面齿轮的转速也最大。

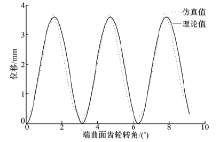
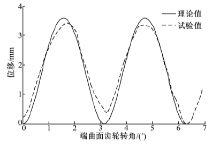
将端曲面齿轮复合运动的模型导入ADAMS仿真软件, 施加相应的约束、载荷及驱动, 如图3所示。仿真得到输出端端曲面齿轮的运动规律, 将其与理论值对比, 如图4所示。

	Figure Option View Download New Window
	图3 端曲面齿轮副复合运动的ADAMS仿真Fig.3 ADAMS simulation of composite motion of curve-face gear pair

从图4可以看出, 端曲面齿轮副的位移的仿真结果随着主动轮转角的变化周期性变化, 而且因为有误差和干扰的存在, 仿真值与理论值存在一定的偏差, 但二者的变化范围都基本相同, 这验证了理论计算结果的正确性。

	Figure Option View Download New Window
	图4 仿真结果与理论值对比Fig.4 Comparison of simulation and theoretical value

2 受力分析

2.1 受力分析

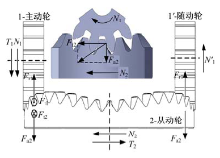
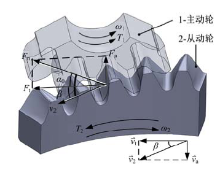
齿轮副啮合过程中的受力状况直接影响传动系统的设计和校核。复合运动端曲面齿轮副啮合过程中的受力状况如图5所示, 图中1为主动轮; 1'为随动轮, 主要用于防止端曲面齿轮出现严重的偏载; 2为从动轮。

	Figure Option View Download New Window
	图5 端曲面齿轮副复合运动的受力状况Fig.5 Force condition of composite motion of curve-face gear

当以直齿圆柱齿轮作为主动轮时:

$F_{t 1} = \frac{T_{1}}{r_{1}} = \frac{(T_{2} + m_{2} β_{2}) / i_{12}}{r_{1}}$ (6)

$F_{r 1} = 0.5 F_{t 1} tanα$ (7)

$F_{t 2} = - F_{t 1}$ (8)

$F_{a 2} = - F_{r 1} = - 0.5 F_{t 1} tanα$ (9)

式中: $\begin{matrix} T_{1} 、 T_{2} \end{matrix}$ 分别为直齿圆柱齿轮和端曲面齿轮的转矩; $\begin{matrix} i_{12} \end{matrix}$ 为齿轮副复合运动的传动比; $\begin{matrix} α \end{matrix}$ 为齿轮副压力角。

2.2 压力角计算

对于端曲面齿轮副复合运动, 其啮合过程中的压力角与标准渐开线齿轮副不同。渐开线上任意一点法向压力的方向线与该点速度方向之间的夹角为该点的压力角。对于端曲面齿轮复合运动, 其压力角即为圆柱齿轮的切向力 $\begin{matrix} {\vec{F}}_{n} \end{matrix}$ 与端曲面齿轮的啮合点的速度 $\begin{matrix} {\vec{v}}_{2} \end{matrix}$ 之间的夹角。如图6所示, 复合运动端曲面齿轮副的压力角 $\begin{matrix} α \end{matrix}$ 等于圆柱齿轮的齿形角 $\begin{matrix} α_{0} \end{matrix}$ 加上切向速度 $\begin{matrix} v_{t} \end{matrix}$ 与合速度 $\begin{matrix} v_{2} \end{matrix}$ 之间的夹角 $\begin{matrix} β 。 \end{matrix}$

	Figure Option View Download New Window
	图6 端曲面齿轮副复合运动的压力角Fig.6 Pressure angle of composite motion of curve-face gear

图6中 $\begin{matrix} ω_{1} 、 ω_{2} \end{matrix}$ 分别为圆柱齿轮和端曲面齿轮的转速; $\begin{matrix} F_{a} 、 F_{t} 、 F_{n} \end{matrix}$ 分别为该齿轮副中端曲面齿轮所受的轴向力、切向力和法向力; $\begin{matrix} {\vec{v}}_{t} 、 {\vec{v}}_{a} 、 {\vec{v}}_{2} \end{matrix}$ 为端曲面齿轮节曲线上一点的切向速度、轴向速度和合速度; $\begin{matrix} β \end{matrix}$ 为切向速度 $\begin{matrix} {\vec{v}}_{t} \end{matrix}$ 与合速度 $\begin{matrix} {\vec{v}}_{2} \end{matrix}$ 之间的夹角; $\begin{matrix} α \end{matrix}$ 为复合运动端曲面齿轮副的压力角:

$\begin{matrix} α = α_{0} + β \end{matrix}$ (10)

式中: $\begin{matrix} β = \arctan ({\vec{v}}_{a} / {\vec{v}}_{t}); α_{0} \end{matrix}$ 为直齿圆柱齿轮压力角, 本文取20° 。

${\vec{v}}_{a} = {\vec{v}}_{2} - {\vec{v}}_{t}$ (11)

$v_{t} = R ω_{2} = R \frac{ω_{1}}{i_{12}}$ (12)

故：

${\vec{v}}_{a} = \sqrt[]{{\vec{v}}_{1}^{2} - {\vec{v}}_{t}^{2}} = \sqrt[]{r^{2} ω_{1}^{2} - R^{2} \frac{ω_{1}^{2}}{i_{12}^{2}}}$ (13)

端曲面齿轮角速度 $\begin{matrix} ω_{2} = ω_{1} / i_{12}; \end{matrix}$ 端曲面齿轮角加速度 $\begin{matrix} β_{2} = \frac{d ω_{2}}{dt}; \end{matrix}$ 圆柱齿轮转矩 $\begin{matrix} T_{1} = \frac{T_{2} + m_{2} β_{2}}{i_{12}} 。 \end{matrix}$

当齿轮副压力角增大时, 齿轮副传递相同的扭矩需要的作用力也越大, 甚至可能出现自锁现象, 通常要求齿轮副压力角最大不能大于65° , 因此有必要对该复合运动齿轮副的压力角进行分析。刀具压力角为20° , 从动轮负载T₂=10 N· m, 分别取直齿圆柱齿轮的齿数为 $\begin{matrix} Z_{1} = 12, 13, 14, 15, \end{matrix}$ 其他参数采用1.2节中参数时, 其压力角变化情况和圆柱齿轮的转矩如图7所示。可以看出, 复合运动端曲面齿轮副的压力角成周期性变化, 但圆柱齿轮齿数对压力角的影响并不明显, 其最大值为36° , 最小值为20° , 处于合理的范围内。

	Figure Option View Download New Window
	图7 齿轮副压力角、圆柱齿轮转矩Fig.7 Pressure angle of gear pair and torque of circular gear

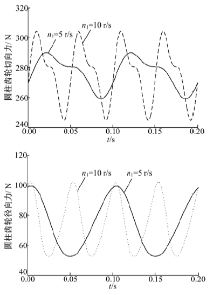
主动轮的转矩变化影响到齿轮副的啮合力, 进而影响对主动轮轴承的设计和校核。由于端曲面齿轮转速并不恒定, 其角加速度的变化对啮合力的影响不可忽视。分别取主动轮转速n₁=5、10 r/s, 其他参数相同的情况下, 主动轮转矩变化如图7所示。可以看出, 当主动轮转速增加时, 圆柱齿轮转矩的波动范围更大, 其最小值更小, 最大值也更大, 这一定程度上决定了复合运动端曲面齿轮副只能用于中低速的场合。而其周期性地改变与转速的增加是等比例的, 因而其随转角变化的周期性并不受转速的影响。

圆柱齿轮的切向力与圆柱齿轮转矩是等比例关系, 而圆柱齿轮径向力还与压力角的变化相关。从图8可以看出, 受压力角变化的影响, 圆柱齿轮径向力的变化规律不同于切向力, 而且其受转速变化的影响相对较小。

	Figure Option View Download New Window
	图8 圆柱齿轮切向力、径向力随转速的变化Fig.8 Variation of tangential force and radical force of circular gear

3 试验验证及对比

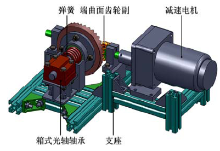
针对这一新型齿轮传动副, 搭建了用于验证其规律的试验平台。由铝型材作为支座, 其余零件除标准件外由树脂材料经工业级3D打印设备加工, 加工出的齿轮实物见图9。

	Figure Option View Download New Window
	图9 3D打印加工的直齿圆柱齿轮与端曲面齿轮Fig.9 Circular gear and curve-face gear manufactured by 3D printing

试验方案如图10所示, 可调速的减速电机通过梅花联轴器连接主动轴, 齿轮副啮合带动端曲面齿轮的旋转/直动运动, 从动轴由箱式光轴轴承支撑, 由弹簧提供从动轴往返的回复力。

	Figure Option View Download New Window
	图10 试验方案Fig.10 Test scheme

	Figure Option View Download New Window
	图11 试验装置及测量设备Fig.11 Test and measurement equipment

最终搭建好的试验平台实物如图11所示。柱齿轮作为主动轮连接电机, 端曲面齿轮作为从动轮, 调速器用于控制电机转速, 激光位移传感器LH-050通过内部的CMOS元件感应并测量输出轴的位移, 控制器用于接受和处理测量数据, 直流电源为控制器和传感器提供24 V直流电源。

通过配套软件LK-Navigator 2控制并观察传感器的数据。调节电机的转速为10 r/min, 试验台平稳运行, 测量输出端的位移。

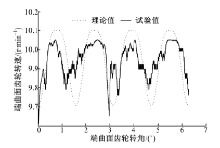
电机最高转速为100 r/min, 调节电机转速, 依次增加20 r/min, 测量其输出轴轴向运动位移, 转速调节至100 r/min时齿轮副依然可以平稳运转。电机转速为10~90 r/min时, 输出轴的最大位移分别为3.517、3.532、3.483、3.532、3.492 mm, 理论最大位移为3.58 mm, 最大误差为0.097 mm, 误差为2.7%, 在误差允许的范围内。复合运动轴向运动的位移测量值如图12所示, 理论值与测量值的对比如图13所示, 图中主动轮转速为30 r/min。从图13可以看出, 端曲面齿轮副的位移随着主动轮转角的变化周期性变化, 测量曲线与理论曲线的变化趋势基本相同。

	Figure Option View Download New Window
	图12 30 r/min时输出轴轴向运动位移Fig.12 Axial displacement of movement at 30 r/min

	Figure Option View Download New Window
	图13 理论位移和测量位移对比Fig.13 Comparison of theoretical displacement to measure displacement

但是因为有制造、安装误差的存在, 试验值与理论值存在一定的偏差。

根据式(2)~(5), 根据测量的位移规律以及已知的转速和齿轮副参数, 反算出端曲面齿轮的转速, 并与理论值对比, 如图14所示。可以看出由试验得出的结果与理论值存在一定的偏差, 但变化趋势基本相同。以上分析表明试验测得的数据是有效的, 也验证了理论计算结果的正确性。

	Figure Option View Download New Window
	图14 理论转速和试验转速对比Fig.14 Comparison of theoretical rotation speed to test speed

4 结论

(1)采用仿真方法验证了端曲面齿轮副复合运动的规律; 设计并搭建了端曲面齿轮复合运动验证试验平台, 验证了其输出轴的复合运动规律, 并与理论值对比, 验证了其正确性。

(2)分析并计算了端曲面齿轮副复合运动的压力角变化规律以及齿轮副啮合力变化规律。齿轮副的压力角受齿轮副齿数的影响比较小, 而齿轮副的啮合力受齿轮副转速的影响, 决定了该齿轮副适用于中、低速的场合, 为该齿轮系统的设计和校核奠定了基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	刘昌祺, 牧野洋, 曹西京. 凸轮机构设计[M]. 北京: 机械工业出版社, 2005: 294-300. [本文引用:1]
[2]	魏引焕. 实现预定轨迹的凸轮连杆组合机构设计[J]. 陕西科技大学学报: 自然科学版, 2012, 30(4): 68-71. Wei Yin-huan. The design of cam-linkage combined mechanisms design for the given locus[J]. Journal of Shanxi University(Science & Technology), 2012, 30(4): 68-71. [本文引用:1]
[3]	薛利峰. 基于齿轮-连杆组合机构的曲轴复合车削刀架系统研究[D]. 武汉: 武汉理工大学机电工程学院, 2012. Xue Li-feng. Research of following turning system of crankshaft based on the combined mechanisn of rod-gear[D]. Wuhan: School of Mechanical and Electronic Engineering, Wuhan University of Technology, 2012. [本文引用:1]
[4]	马良, 石宁. 齿轮-五杆组合机构运动学特征仿真分析[J]. 西安科技大学学报, 2013, 35(6): 727-730, 764. Ma Liang, Shi Ning. Gear-5-bar combination mechanism's kinematics characteristic simulation[J]. Journal of Xi'an University of Science and Technology, 2013, 35(6): 727-730, 764. [本文引用:1]
[5]	Ottaviano E, Mundo D, Danieli G A, et al. Numerical and experimental analysis of non-circular gears and cam-follower systems as function generators[J]. Mechanism and Machine Theory, 2008, 43(8): 996-1008. [本文引用:1]
[6]	邹慧君, 张青, 王学武. 组合机构的基本特征和设计方法[J]. 机械设计与研究, 2006, 22(1): 16-19. Zou Hui-jun, Zhang Qing, Wang Xue-wu. Basic characteristic and design method of the composite-mechanism[J]. Machine Design and Research, 2006, 22(1): 16-19. [本文引用:1]
[7]	林超, 张雷, 张志华. 一种新型非圆锥齿轮副的传动原理及其齿面求解[J]. 机械工程学报, 2014, 50(13): 66-72. Lin Chao, Zhang Lei, Zhang Zhi-hua. Transmission theory and tooth surface solution of a new type of non-circular bevel gears[J]. Journal of Mechanical Engineering, 2014, 50(13): 66-72. [本文引用:2]
[8]	Lin Chao, Liu Yi. Characteristic analysis and application of composite motion curve-face gear pair[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2016, 38(6): 1797-1804. [本文引用:2]
[9]	林超, 龚海. 复合传动变传动比面齿轮副[P]. 中国: 2011104394780, 2012-06-27. [本文引用:1]
[10]	Lin Chao, Gong Hai, Ning Nie, et al. Geometry design, 3D modeling and kinematics analysis of orthogonal fluctuating gear ratio face gear drive[J]. Journal of Mechanical Engineering Science, 2013, 227(4): 779-793. [本文引用:2]

2005

0.0

... 0 引言常见的组合机构有实现预定轨迹要求的联动凸轮组合机构、凸轮-连杆组合机构、实现任意停歇或复杂运动规律要求的凸轮-齿轮组合机构、实现多种运动规律及轨迹要求的齿轮-连杆组合机构和齿轮与液压的组合机构等^{[1,2,3,4,5,6]} ...

2012

0.0

2012

0.0

2013

0.0

2008

0.0

2006

0.0

2014

0.0

... 复合运动齿轮副包含正交复合运动锥齿轮副^[7]、正交复合运动端曲面齿轮副^[8]、复合运动面齿轮副^[9]、复合运动非圆齿轮副和非圆齿轮齿条运动副 ...

... 针对端曲面齿轮的研究已经比较详尽,而端曲面齿轮副复合运动的研究却比较少,集中在齿面求解、运动规律的计算和应用方面^[7,10] ...

2016

0.0

... 2 运动规律当以直齿圆柱齿轮为主动轮时,输出端轴向位移的运动规律为^[8]: ...

2012

0.0

2013

0.0

... 其中端曲面齿轮复合运动机构是在端曲面齿轮基础上提出的结合了凸轮机构、齿轮机构和非圆齿轮机构特点的一种新型的齿轮传动^[10] ...

... 针对端曲面齿轮的研究已经比较详尽,而端曲面齿轮副复合运动的研究却比较少,集中在齿面求解、运动规律的计算和应用方面^[7,10] ...