基于故障相关性分析的数控机床系统可靠性建模

引用本文

张英芝, 刘津彤, 申桂香, 戚晓艳, 龙哲. 基于故障相关性分析的数控机床系统可靠性建模. 2017, 47(1): 169-173
ZHANG Ying-zhi, LIU Jin-tong, SHEN Gui-xiang, QI Xiao-yan, LONG Zhe. Reliability modeling of CNC machine tools system based on failure correlation analysis. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 169-173 复制到剪切板

Permissions

基于故障相关性分析的数控机床系统可靠性建模

张英芝¹, 刘津彤¹, 申桂香¹, 戚晓艳^1,², 龙哲¹

1.吉林大学机械科学与工程学院,长春 130022

2.空军航空大学飞行器与动力系,长春 130022

通讯作者:申桂香(1957-),女,教授,博士生导师.研究方向:数控装备及其全生命周期工程.E-mail:shengx@jlu.edu.cn

作者简介:张英芝(1970-),女,副教授,博士.研究方向:数控装备可靠性工程.E-mail:zhangyz@jlu.edu.cn

基金:国家自然科学基金项目(51275205); 吉林省自然科学基金项目(20150101025JC); 高档数控机床与基础制造装备科技重大专项项目(2015ZX04003002).

摘要

基于数控机床相关故障机理分析进行组件可靠性建模,并以组件可靠性模型为边缘分布,引入Copula函数,建立联合可靠性函数,通过样本得到Kendall秩相关系数来进行Copula函数参数估计,为相关故障条件下系统可靠性分析提供一种新的技术方法。最后,以加工中心为例,将本文方法与采用传统方法的组件可靠性串联模型、不考虑故障相关方向性的Copula函数模型进行对比,结果证明了模型的合理性和有效性。

关键词: 机床; 故障相关; 平均秩次法; 可靠性建模; Copula函数; Kendall秩相关系数

中图分类号:TG659 文献标志码:A 文章编号:1671-5497(2017)01-0169-05

Reliability modeling of CNC machine tools system based on failure correlation analysis

ZHANG Ying-zhi¹, LIU Jin-tong¹, SHEN Gui-xiang¹, QI Xiao-yan^1,², LONG Zhe¹

1.College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China

2.Department of Aircraft and Driving Force, Aviation University of Air Force, Changchun 130022,China

Abstract

A new technical approach is proposed for the reliability analysis of CNC machine tools system under the failure correlation. First, the component reliability models were built based on related failure mechanism analysis. Then, taking the component reliability models as the marginal distribution, the system joint reliability function was developed with the introduction of the Copula function. Third, the parameter of Copula function was estimated with the aid of Kendall rank correlation coefficient obtained from samples. Finally, a case study of machining center is carried out. Comparing with the component reliability series model and with the traditional Copula function model, the new Copula function model considering failure correlation directionality is ore rational and effective.

Keyword: machine tool; failure correlation; average rank time method; reliability modeling; Copula function; Kendall rank correlation coefficient

Show Figures

0 引言

数控机床是典型的机、电、液一体化复杂系统, 相关是其故障普遍特征, 尤其是相关关系方向性的存在, 给系统可靠性建模带来困难。

目前, 相关故障研究方法很多。Ditlevsen^[1]提出用二阶窄界方法进行故障模式相关性的可靠性区间估算, 但当故障模式样本较大时, 实现过程复杂且难以推广。Parkinson^[2]基于零件间失效相关性推导出串联组件可靠性的上下界, 计算出任意两子部件的联合可靠性。Zhao等^[3]给出同时适用于串联和并联系统的矩近似方法可靠度求解, 该点估计方法不需要进行蒙特卡洛仿真就可以对系统初始时刻的性能函数进行评价。Feng^[4]通过一阶、二阶和三阶联合概率来表达系统可靠性。Ang等^[5]提出用一些特定故障模式代替系统所有故障模式或者对故障模式相关系数进行分类, 借助概率网络估算技术对故障相关系统可靠性进行计算。胡秀庄^[6]引入相关性参数, 利用模系运算算子实现除串联系统以外其他失效相关系统的可靠性计算。在不可修系统失效相关分析中, 张庆功^[7]对传统限制相关参数的哈马邱尔算子的缺陷进行改进, 用蒙特卡洛模型证明其合理性。赵靖等^[8]提出基于故障相关性、考虑测试、运行环境的软件非齐次泊松过程(NHPP)模型。任震等^[9]提出考虑相关故障的输电线路可靠性等效模型。当前, Copula函数被频繁应用在故障相关系统可靠性建模中^[10], 该方法在参数估计中多采用极大似然估计, 在一定正则条件下, 它是渐近有效估计, 即渐近正态, 但该方法计算繁琐, 还有可能不收敛。

纵观国内外研究现状表明, 当前对相关故障问题的研究多基于可靠性结构模型或随机过程模型, 很少考虑故障传播方向, 即使考虑到这点, 如文献^[5], 也因故障模式简化, 计算结果存在一定误差。

数控机床系统相关故障属于故障传播型, 即第二类相关故障。本文应用因果图明确系统组件间故障相关方向并建立组件可靠性模型, 以此模型为边缘分布, 引入Copula函数建立系统联合可靠度模型, 通过样本得到Kendall秩相关系数来进行参数估计, 为相关故障条件下系统可靠性分析提供一种新方法。最后以加工中心为例, 将该方法与传统组件可靠性串联模型、不考虑故障相关方向性的Copula函数模型进行对比, 验证了模型的合理性和有效性。

1 相关故障关系分析

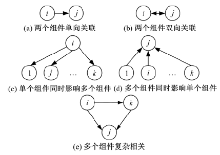
相关故障传递中同时存在着影响组件和被影响组件, 两类组件统称为相关组件。考虑到故障传递中相关组件数量和故障作用形式等问题, 以圆圈表示组件, 有向线段表示故障传递方向, 据此图1归纳总结了5种相关故障关系^[11]。其中, 前4种是最基本的相关故障关系, 可以组合成任意复杂相关关系, 图1(e)为一种多组件的复杂相关关系。

	Figure Option View Download New Window
	图1 相关故障关系类型图Fig.1 Relationship types of related failures

图1中, (a)、(c)、(d)、(e)的组件 $\begin{matrix} i \end{matrix}$ 只与有向线段的起点相连, 表示只影响其他组件, 该组件定义为相关故障的起点; 反之, (a)、(c)、(d)、(e)中的组件 $\begin{matrix} j \end{matrix}$ , 定义为相关故障的终点; (e)中的组件 $\begin{matrix} k \end{matrix}$ , (b)中的组件 $\begin{matrix} i \end{matrix}$ 、 $\begin{matrix} j \end{matrix}$ 既是影响组件又是被影响组件, 定义为相关故障的中间点。

如果相关故障的起点为组件 $\begin{matrix} i, \end{matrix}$ 组件 $\begin{matrix} i \end{matrix}$ 即为故障部位, 故障时间即为组件 $\begin{matrix} i \end{matrix}$ 的故障时间。因此, 进行组件可靠性建模前除了要进行传统故障分析, 还应进行相关故障方向性分析, 确定故障起点, 进而确定组件故障时间。

2 组件可靠性建模

目前多数产品都采用定时截尾可靠性试验, 即试验到某一规定时间即停止试验, 但考虑到各试验样本的试验开始时间可能不一致, 因此试验数据会出现随机逐次截尾^[12]的特点。同时考虑其他组件故障产生截尾数据带来的时间相关影响, 因此此类试验数据又具备多重截尾的特性。

参考文献^[12], 用平均秩次代替原秩次, 再利用中位秩公式计算这种多重截尾数据的经验分布函数 $\begin{matrix} F (t_{i}) 。 \end{matrix}$

选择工程中常用的威布尔分布作为假设模型, 采用最小二乘法进行模型参数估计, 采用 $\begin{matrix} D \end{matrix}$ 检验法进行假设检验。

3 系统可靠性建模

以组件可靠性模型为边缘分布, 引入Cumbel Copula连接函数, 建立系统联合可靠度函数模型, 并进行参数估计和分布拟合检验。

3.1 系统联合可靠度函数模型建立

针对图1中类型(e), $\begin{matrix} i, k \end{matrix}$ 均影响 $\begin{matrix} j, \end{matrix}$ 先建立组件 $\begin{matrix} i, k \end{matrix}$ 的联合可靠度函数 $\begin{matrix} R_{i \to k}, \end{matrix}$ 然后以 $\begin{matrix} R_{i \to k} \end{matrix}$ 与 $\begin{matrix} R_{j} \end{matrix}$ 为边缘分布, 建立系统联合可靠度函数 $\begin{matrix} R_{(i \to k) \to j} 。 \end{matrix}$

假设数控机床系统各组件的可靠性函数分别为 $\begin{matrix} R_{1} (t) 、 R_{2} (t) 、 \dots 、 R_{n} (t), \end{matrix}$ 则系统联合可靠性函数为:

$\begin{matrix} \begin{matrix} C (R_{1} (t) 、 R_{2} (t) 、 \dots 、 R_{n} (t)) = \\ \exp \{- [{(- \ln R_{1} (t))}^{θ} + \\ {(- \ln R_{2} (t))}^{θ} + \dots + {{(- \ln R_{n} (t))}^{θ}]}^{1 / θ}\} = \\ \exp \{- {[\overset{n}{\sum_{i = 1}} (- \ln R_{i} {(t))}^{θ}]}^{1 / θ}\} \end{matrix} \end{matrix}$ (1)

式中: $\begin{matrix} θ \in (1, + \infty] 。 \end{matrix}$

3.2 参数估计

参考文献^[13]定理1, 设 $\begin{matrix} X \end{matrix}$ 和 $\begin{matrix} Y \end{matrix}$ 是随机变量, 其Copula是生成元为 $\begin{matrix} φ (t) \end{matrix}$ 的Archimedean Copula, 则 $\begin{matrix} X \end{matrix}$ 和 $\begin{matrix} Y \end{matrix}$ 的Kendall秩相关系数 $\begin{matrix} τ \end{matrix}$ 为:

$\begin{matrix} τ = 1 + 4 \int_{0}^{1} [φ (t) / φ' (t)] dt \end{matrix}$ (2)

式中: $\begin{matrix} φ (t) \end{matrix}$ 为Copula函数的生成函数, 对于Cumbel Copula函数而言, 其表达式为: $\begin{matrix} φ (t) = {(- lnt)}^{θ}, θ \in [1, + \infty), \end{matrix}$ 从而可计算出: $\begin{matrix} τ = 1 - 1 / θ, θ \in [1, + \infty) 。 \end{matrix}$

考虑Cumbel Copula函数的对称性, Cumbel Copula函数是可交换的, 可用样本和Cumbel Copula函数是可交换的这一信息去估计总体的Kendall秩相关系数 $\begin{matrix} τ', \end{matrix}$ 其表达式为:

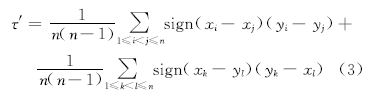
式中: $\begin{matrix} τ' \end{matrix}$ 是Kendall秩相关系数τ 的无偏估计; $\begin{matrix} sign (x) \end{matrix}$ 为符号函数, 其表达式为:

$\begin{matrix} sign (x) = \{\begin{matrix} 1, x > 0 \\ 0, x = 0 \\ - 1, x < 0 \end{matrix} \end{matrix}$ (4)

综上可得到Copula函数参数估计的表达式:

$\begin{matrix} θ = \frac{1}{1 - τ} = \frac{1}{1 - τ'}, θ \in [1, + \infty) \end{matrix}$ (5)

4 实例

4.1 相关故障关系分析

参考文献[14], 对6台某型号加工中心进行随机逐次截尾试验, 对所发生的故障数据进行记录分析, 据此得到加工中心组件故障数据表(见表1), 表中“ * ” 表示相关故障数据。

表1 加工中心组件故障数据表 Table 1 Failure data of machining center components

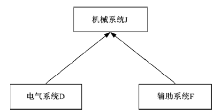
由表1的故障数据, 通过故障因果关系分析得3个组件故障相关关系, 如图2所示。

	Figure Option View Download New Window
	图2 组件故障相关关系图Fig.2 Failure correlation relationship among components

4.2 组件可靠性建模

参考文献^[12], 得到电气系统、辅助系统、机械系统三个组件的可靠性模型分别为:

$\begin{matrix} \{\begin{matrix} R_{D} = \exp [- {(\frac{t}{810.545})}^{0.597}] \\ R_{F} = \exp [- {(\frac{t}{462.776})}^{1.688}] \\ R_{J} = \exp [- {(\frac{t}{1679.793})}^{0.638}] \end{matrix} \end{matrix}$

4.3 系统可靠性建模

根据图2可知, 电气系统、辅助系统两组件均影响机械系统。所以, 先引入Copula连接函数, 建立电气系统、辅助系统两组件的部分系统联合可靠度函数模型 $\begin{matrix} R_{D - F}; \end{matrix}$ 再以 $\begin{matrix} R_{D - F} 、 R_{J} \end{matrix}$ 为边缘分布, 引入Copula连接函数, 建立系统联合可靠度函数模型 $\begin{matrix} R_{SYS_X} 。 \end{matrix}$

由三组件可靠度函数可知:

$R_{D - F} = R_{D} \times R_{F} = \exp \{- [{(\frac{t}{810.545})}^{0.597} + {(\frac{t}{462.776})}^{1.688}]\}$ (6)

$R_{SYS_X} = C (R_{D - F} (t), R_{J} (t)) = \exp \{- {[(- \ln R_{D - F} {(t))}^{θ} + (- \ln R_{J} {(t))}^{θ}]}^{1 / θ}\}$ (7)

将三组件的故障数据及相应可靠性函数带入式(6)(7), 可以计算出式(7)中参数值: $\begin{matrix} θ = 2.284, \end{matrix}$ 则:

$\begin{matrix} \begin{matrix} R_{SYS_X} = \\ \exp \{- \{{[{(\frac{t}{810.545})}^{0.597} + {(\frac{t}{462.776})}^{1.688}]}^{2.284} + \\ {(\frac{t}{1679.793})}^{1.457}\}^{0.438}\} \end{matrix} \end{matrix}$

若不考虑加工中心机械系统、电气系统和辅助系统之间的故障影响方向性, 直接引入Copula函数建立整个加工中心系统可靠性模型:

$R_{SYS_Y} = C (R_{J} (t), R_{D} (t), R_{F} (t)) = \exp \{- [{(- \ln R_{J} (t))}^{\hat{θ}} + {{(- \ln R_{D} (t))}^{\hat{θ}} + {(- \ln R_{F} (t))}^{\hat{θ}}]}^{1 / \hat{θ}}\}$ (8)

将联合可靠性函数与故障间隔时间结合, 利用Matlab进行编程运算, 调用MLE似然函数, 可得Copula函数的参数 $\begin{matrix} \hat{θ} = 3.788, \end{matrix}$ 则:

$\begin{matrix} \begin{matrix} R_{SYS_Y} = \\ \exp \{- [{(\frac{t}{810.545})}^{2.261} + {(\frac{t}{462.776})}^{6.394} + \\ {{(\frac{t}{1679.793})}^{2.417}]}^{0.264}\} \end{matrix} \end{matrix}$

基于故障独立假设下系统可靠度函数为:

$\begin{matrix} \begin{matrix} R_{SYS_D} = R_{J} \times R_{D} \times R_{F} = \\ \exp [- {(\frac{t}{1679.793})}^{0.638}] \times \exp [- {(\frac{t}{810.545})}^{0.597}] \times \\ \exp [- {(\frac{t}{462.776})}^{1.688}] \end{matrix} \end{matrix}$ (9)

通过拟合性检验, 由于 $\begin{matrix} D_{n} < D_{n, α}, \end{matrix}$ 所以接受原假设, 可靠性模型符合假设分布。

以故障时间为横坐标, 分别以组件故障独立R_{SYS_D} 、故障相关假设下系统可靠度函数 $\begin{matrix} R_{SYS_X} 、 R_{SYS_Y} \end{matrix}$ 为纵坐标, 绘制如图3所示曲线。

	Figure Option View Download New Window
	图3 可靠度函数曲线对比图Fig.3 Comparison of reliability function curves

由图3和表2可以发现, 考虑组件相关故障影响方向性的联合可靠度模型 $\begin{matrix} R_{SYS_X} \end{matrix}$ 较串联模型可靠度 $\begin{matrix} R_{SYS_D} \end{matrix}$ 下降缓慢。同时若不考虑组件影响方向, 其联合可靠度模型 $\begin{matrix} R_{SYS_Y} \end{matrix}$ 会远大于以上两种可靠度模型, 因为 $\begin{matrix} R_{SYS_Y} \end{matrix}$ 对组件的故障影响关系方向缺乏确切地反映, 与实际相比其可靠度值明显偏大。由此可知, 考虑组件故障影响关系方向的联合可靠度模型 $\begin{matrix} R_{SYS_X} \end{matrix}$ 较其余两种可靠度模型更合理、更符合实际。

表2 可靠度值对比 Table 2 Comparison of reliability values

可靠度值	时间/h
可靠度值	10	50	100	200	300	400
$\begin{matrix} R_{SYS_X} \end{matrix}$	0.92	0.79	0.68	0.49	0.34	0.23
$\begin{matrix} R_{SYS_D} \end{matrix}$	0.89	0.73	0.59	0.39	0.25	0.16
$\begin{matrix} R_{SYS_Y} \end{matrix}$	0.93	0.82	0.74	0.63	0.53	0.41

表2 可靠度值对比 Table 2 Comparison of reliability values

5 结论

(1)针对试验数据是多重截尾数据与故障数据并存的组件可靠性建模问题, 首先引入平均秩次法对故障秩次予以修正, 既考虑试验截尾, 又考虑组件故障截尾; 再利用中位秩公式计算组件的经验分布函数。该方法具有很强的理论支撑, 且计算过程简洁, 结果精确度也相对较高。

(2)采用Copula连接函数构建整机模型, 来描述组件之间的故障相关性, 最终得到三类系统联合可靠度模型并进行对比分析, 考虑组件相关故障影响方向性的Copula联合可靠度模型较基于组件故障独立假设下串联模型可靠度下降的缓慢, 较不考虑组件影响方向的Copula联合可靠度模型更加平缓, 即模型更加合理、更符合工程实际。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ditlevsen O. Narrow reliability bounds for structural systems[J]. Journal of Structural Mechanics, 1979, 7(4): 453-472. [本文引用:1]
[2]	Parkinson D B. Reliability bounds for dependent failures[J]. IEEE Transactions on Reliability, 1988, 37(1): 54-56. [本文引用:1]
[3]	Zhao Y G, Ang A H S. System reliability assessment by method of moments[J]. Journal of Structural Engineering, 2003, 129(10): 1341-1349. [本文引用:1]
[4]	Feng Yuan-sheng. A method for computing structural system reliability with high accuracy[J]. Computers & Structures, 1989, 33(1): 1-5. [本文引用:1]
[5]	Ang A H S, Ma H F. On the reliability analysis of framed structures[C]//The 4th ASCE Speciality Conference on Probabilistic Mechanics and Structural Reliability, Tucson, 1979: 106-111. [本文引用:2]
[6]	胡秀庄. 具有中介状态和失效相关时抗震建筑结构可靠性分析研究[D]. 成都: 西南石油大学石油与天然气工程学院, 2004. Hu Xiu-zhuang. Study on the reliability analysis of aseismic building structure with intermediate state and failure dependence[D]. Chengdu: College of Petroleum and Natural Gas Engineering, Southwest Petroleum University, 2004. [本文引用:1]
[7]	张庆功. 考虑失效相关时不可修复工程系统的可靠性分析[D]. 成都: 西南石油大学机电工程学院, 2004. Zhang Qing-gong. Reliability analysis of unrepairable engineering system considering failure dependence[D]. Chengdu: College of Mechatronics Engineering, Southwest Petroleum University, 2004. [本文引用:1]
[8]	赵靖, 张汝波, 顾国昌. 考虑故障相关的软件可靠性增长模型研究[J]. 计算机学报, 2007, 30(10): 1713-1720. Zhao Jing, Zhang Ru-bo, Gu Guo-chang. Study of software reliability growth model considering failure dependency[J]. Chinese Journal of Computers, 2007, 30(10): 1713-1720. [本文引用:1]
[9]	任震, 梁振升, 黄雯莹. 考虑相关故障的双回输电线路可靠性评估[J]. 电力自动化设备, 2005, 25(6): 14-17. Ren Zhen, Liang Zhen-sheng, Huang Wen-ying. Reliability evaluation of two parallel transmission lines with respect to relevant fault[J]. Electric Power Automation Equipment, 2005, 25(6): 14-17. [本文引用:1]
[10]	张英芝, 郑锐, 申桂香, 等. 基于Copula理论的数控装备故障相关性[J]. 吉林大学学报: 工学版, 2011, 41(6): 1636-1639. Zhang Ying-zhi, Zheng Rui, Shen Gui-xiang, et al. Failure dependency of CNC equipment based on copula theory[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(6): 1636-1639. [本文引用:1]
[11]	王晓燕, 申桂香, 张英芝, 等. 基于故障链的复杂系统故障相关系数建模[J]. 吉林大学学报: 工学版, 2015, 45(2): 442-447. Wang Xiao-yan, Shen Gui-xiang, Zhang Ying-zhi, et al. Dependent coefficient model for complex system based on failure chains[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(2): 442-447. [本文引用:1]
[12]	申桂香, 孟书, 张英芝, 等. 平均秩次法在组件可靠性建模中的应用[J]. 吉林大学学报: 工学版, 2014, 44(1): 101-105. Shen Gui-xiang, Meng Shu, Zhang Ying-zhi, et al. Application of average rank time method in reliability modeling for subsystems[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(1): 101-105. [本文引用:3]
[13]	杜江, 陈希镇, 于波. Archimedean Copula 函数的参数估计[J]. 科学技术与工程, 2009, 9(3): 637-640. Du Jiang, Chen Xi-zhen, Yu Bo. Parameter estimation of Archimedean Copula[J]. Science Technology and Engineering, 2009, 9(3): 637-640. [本文引用:1]
[14]	申桂香, 贾亚洲, 马健, 等. CNC机床故障分析及其可靠性[J]. 中国机械工程, 1996, 7(6): 67-69. Shen Gui-xiang, Jia Ya-zhou, Ma Jian, et al. CNC machine tool failure analysis and reliability[J]. China Mechanical Engineering, 1996, 7(6): 67-69. [本文引用:1]

1979

0.0

... Ditlevsen^[1]提出用二阶窄界方法进行故障模式相关性的可靠性区间估算,但当故障模式样本较大时,实现过程复杂且难以推广 ...

1988

0.0

... Parkinson^[2]基于零件间失效相关性推导出串联组件可靠性的上下界,计算出任意两子部件的联合可靠性 ...

2003

0.0

... Zhao等^[3]给出同时适用于串联和并联系统的矩近似方法可靠度求解,该点估计方法不需要进行蒙特卡洛仿真就可以对系统初始时刻的性能函数进行评价 ...

1989

0.0

... Feng^[4]通过一阶、二阶和三阶联合概率来表达系统可靠性 ...

1979

0.0

... Ang等^[5]提出用一些特定故障模式代替系统所有故障模式或者对故障模式相关系数进行分类,借助概率网络估算技术对故障相关系统可靠性进行计算 ...

... 纵观国内外研究现状表明,当前对相关故障问题的研究多基于可靠性结构模型或随机过程模型,很少考虑故障传播方向,即使考虑到这点,如文献^[5],也因故障模式简化,计算结果存在一定误差 ...

2004

0.0

... 胡秀庄^[6]引入相关性参数,利用模系运算算子实现除串联系统以外其他失效相关系统的可靠性计算 ...

2004

0.0

... 在不可修系统失效相关分析中,张庆功^[7]对传统限制相关参数的哈马邱尔算子的缺陷进行改进,用蒙特卡洛模型证明其合理性 ...

2007

0.0

... 赵靖等^[8]提出基于故障相关性、考虑测试、运行环境的软件非齐次泊松过程(NHPP)模型 ...

2005

0.0

... 任震等^[9]提出考虑相关故障的输电线路可靠性等效模型 ...

2011

0.0

. 2011, 41(6):1636-1639

Failure dependency of CNC equipment based on copula theory

基于Copula理论的数控装备故障相关性

Zhang Ying-zhi , Zheng Rui , Shen Gui-xiang

张英芝, 郑锐, 申桂香

1.College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China|2.The 716th Research Institute of China Shipbuilding Industry Corporation,Lianyungang 222006,China

The reliability analysis was performed for the related failures using the Copula theory, selecting the Gumbel Copula function in the Archimedes function group as the linking function of the CNC machine tool to establish the relationship between the complete machine and its subsystems. The parameters of Copula function were estimated by the genetic algorithm. Comparing with the series model, the failure analysis based on the Copula theory is more accurate.

应用Copula理论进行相关故障下的可靠性分析,选取阿基米德函数族中的Gumbel Copula函数作为数控机床的连接函数,建立了整机与子系统之间的故障相依关系。然后,利用遗传算法对Copula函数中的参数进行估计。与串联模型的比较表明,基于Copula理论的故障分析结果更加符合实际。

... 当前,Copula函数被频繁应用在故障相关系统可靠性建模中^[10],该方法在参数估计中多采用极大似然估计,在一定正则条件下,它是渐近有效估计,即渐近正态,但该方法计算繁琐,还有可能不收敛 ...

2015

0.0

. 2015, 45(2):442-447 DOI:10.13229/j.cnki.jdxbgxb201502016

Dependent coefficient model for complex system based on failure chains

基于故障链的复杂系统故障相关系数建模

Wang Xiao-yan , Shen Gui-xiang , Zhang Ying-zhi

王晓燕, 申桂香, 张英芝

1.College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China; 2.Department of Electronic Engineering, Shenyang Aerospace University, Shenyang 110136, China; 3.Department of Aircrafe and Driving Force,Aviation University of Air Force, Changchun 130022,China

The degree of interaction between dependent systems determines the error between the theory reliability and field reliability. So the dependent coefficient between the dependent systems is an important reference for design reliability and distribution reliability. However, the existing method can only estimate the dependent coefficient of a simple chain which includes two systems. In this work, the interaction in failure chains is classified after investigating large amount of failure data. Based on the types of failure chains, a model of dependent coefficient for complex system is developed using the function relationships among the dependent failure rate, independent failure rate and dependent coefficient of subsystems. A case study is carried out to verify the developed model. Results show that the model can estimate the dependent coefficient of a complex system, and improve the theory. It is very important to more precisely design the reliability growth and to optimize the repair and maintenance schedules.

基于大量故障数据分析，对故障链类型进行分类。利用子系统相关故障率、相关系数和独立故障率之间的关系，建立了复杂系统故障相关系数模型，并以实例验证。本文解决了多系统复杂相关关系的相关系数计算问题，完善了相关系数理论体系，对精确可靠性设计、优化维修计划具有重要意义。

... 考虑到故障传递中相关组件数量和故障作用形式等问题,以圆圈表示组件,有向线段表示故障传递方向,据此图1归纳总结了5种相关故障关系^[11] ...

2014

0.0

. 2014, 44(1):101-105 DOI:10.13229/j.cnki.jdxbgxb201401018

Application of average rank time method in reliability modeling for subsystems

平均秩次法在组件可靠性建模中的应用

Shen Gui-xiang , Meng Shu , Zhang Ying-zhi

申桂香, 孟书, 张英芝

1. College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China; 2. College of Management, Jilin University, Changchun 130022, China

This paper presents a method of the reliability modeling of a series system. Such a system is composed of several mutual independent subsystems, and the system life-time obeys two-parameter Weibull distribution. In this method, when one of subsystems is failure, the fault data of the other subsystems are processed as censored data, and the failure sequence is revised using the average rank time method. This method can be applied for model parameter estimation and fitting test to reduce the modeling error and improve the accuracy. Finally, as a case study, the real data of a Computerized Numerical Control (CNC) are used to demonstrate the application of the proposed method, which verifies the effectiveness and applicability of the method.

讨论了由几个相互独立的子系统组成的串联系统的寿命服从两参数威布尔分布时，其子系统的可靠性建模问题。并指出当某子系统出现故障时，其他子系统故障数据按照截尾数据处理，然后用平均秩次法对故障顺序修正，据此进行模型参数估计和拟合性检验，可以达到减小建模误差、提高拟合精度的目的。最后以某加工中心现场试验数据为例介绍该方法的具体应用过程，以验证该方法的有效性和实用性。

... 2 组件可靠性建模目前多数产品都采用定时截尾可靠性试验,即试验到某一规定时间即停止试验,但考虑到各试验样本的试验开始时间可能不一致,因此试验数据会出现随机逐次截尾^[12]的特点 ...

... 参考文献^[12],用平均秩次代替原秩次,再利用中位秩公式计算这种多重截尾数据的经验分布函数 F(ti) ...

... 2 组件可靠性建模参考文献^[12],得到电气系统、辅助系统、机械系统三个组件的可靠性模型分别为: ...

2009

0.0

... 2 参数估计参考文献^[13]定理1,设 X和 Y是随机变量,其Copula是生成元为 φ(t)的Archimedean Copula,则 X和 Y的Kendall秩相关系数 τ为: ...

1996

0.0