基于降维算法的结构可靠性分析

引用本文

孟广伟, 冯昕宇, 周立明, 李锋. 基于降维算法的结构可靠性分析. 2017, 47(1): 174-179
MENG Guang-wei, FENG Xin-yu, ZHOU Li-ming, Li Feng. Structural reliability analysis based on dimension reduction algorithm. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 174-179 复制到剪切板

Permissions

基于降维算法的结构可靠性分析

孟广伟, 冯昕宇, 周立明, 李锋

吉林大学机械科学与工程学院,长春 130022

通讯作者:李锋(1977-),男,副教授,博士.研究方向:疲劳与断裂.E-mail:fengli@jlu.edu.cn

作者简介:孟广伟(1959-),男,教授,博士生导师.研究方向:疲劳与断裂.E-mail:mgw@jlu.edu.cn

基金:国家重大科学仪器设备开发专项项目(2012YQ030075); 吉林省科技发展计划项目(201205001,201215048).

摘要

为解决工程实际中功能函数为高维非线性的可靠性分析问题,提出了基于降维算法的一种新型的直接结构可靠度的分析方法。利用降维算法,建立了新的 n个一维函数模型近似替代原 n维功能函数,借助于泰勒级数和统计矩理论,求解结构功能函数的前四阶矩信息,并通过Edgeworth级数拟合结构功能函数的累积分布函数,结合可靠性理论可计算得到结构的失效概率。与传统方法相比,本文方法无需积分求解功能函数的统计矩,也无需迭代搜索最可能失效点。数值算例结果表明本文方法具有较高的计算精度和较好的适应性。

关键词: 工程力学; 可靠性分析; 降维算法; 泰勒级数; Edgeworth级数; 矩方法

中图分类号:TB114.3 文献标志码:A 文章编号:1671-5497(2017)01-0174-06

Structural reliability analysis based on dimension reduction algorithm

MENG Guang-wei, FENG Xin-yu, ZHOU Li-ming, Li Feng

College of Mechanical Science and Engineering,Jilin University,Changchun 130022,China

Abstract

Considering the high-dimensional non-linear performance functions of complex structures, a new structural reliability analysis method based on dimension reduction algorithm was proposed. The n one-dimensional approximate functions were established to substitute the n dimensional performance function by using dimension reduction algorithm. With the help of Taylor series and statistical moment theory, the first four order moments of the performance function were solved. The cumulative distribution function of the performance function was fitted by Edgeworth series and the failure probability of the structure was obtained based on the reliability theory. Compared with the traditional methods, the new method does not need to use integral method to solve the statistical moments of the performance function, and not need to search the most possible failure point iteratively. Numerical results indicate that the proposed method has high precision and good adaptability.

Keyword: engineering mechanics; reliability analysis; dimension reduction method; Taylor series; Edgeworth series; moment method

Show Figures

在工程实际中, 经常会遇到大量功能函数为高维非线性的复杂结构问题, 要考虑结构的不确定性变量和结构设计的安全性, 因而可用可靠度方法来解决此类问题^{[1, 2]}。对于可靠度分析的常见方法有解析法^{[3, 4]}、梯度法^{[5, 6, 7]}和数值模拟法^{[8, 9]}等。解析法只有在规则的区域内且函数简单时才能直接进行积分求解; 在梯度方法中需在概率密度最大的相关点处求解功能函数的梯度, 未考虑到功能函数在设计验算点附近的局部性质和功能函数的非线性程度等。而数值模拟法虽对计算求解无限制, 计算精度较高、编程相对简单, 但对于小概率问题和大型结构系统, 其计算的工作量及耗时往往难以忍受, 较难满足工程的需求。

因此, 本文提出一种基于降维算法^[10]的直接结构可靠性分析方法。运用降维思想, 利用 $\begin{matrix} n \end{matrix}$ 个一维函数近似表达高维函数, 构造成新的函数模型, 借助于泰勒级数展开法与统计矩理论, 通过计算获得结构功能函数的前四阶中心矩, 再运用Edgeworth^{[11, 12, 13]}级数法, 可拟合结构功能函数的累积分布函数和概率密度函数, 最后结合可靠性理论计算得到结构的失效概率。

1 降维算法

可靠性问题的失效概率为:

$\begin{matrix} P_{f} = P (g (x) \leq 0) = \int_{g (x) \leq 0} f (x) dx \end{matrix}$ (1)

式中: $\begin{matrix} x = {x_{1}, x_{2}, \dots, x_{N}}^{T} \end{matrix}$ 代表N维向量; $\begin{matrix} g (x) \end{matrix}$ 为结构功能函数, 如 $\begin{matrix} g (x) \leq 0 \end{matrix}$ 表示结构失效; $\begin{matrix} f (x) \end{matrix}$ 为输入随机变量的联合概率密度函数。

降维算法是一种维度分解方法, 主要是利用分解的思想, 将一个 $\begin{matrix} N \end{matrix}$ 维函数分解为S(S< N, 本文取S=1)维函数和的形式, 不需求解矩阵的逆, 计算效率较高。

将结构功能函数 $\begin{matrix} g (x) \end{matrix}$ 在最可能失效点(MPP)处进行泰勒级数展开, 设MPP点为 $\begin{matrix} x = [μ_{1}^{*}, \dots, μ_{N}^{*}]^{T}, \end{matrix}$ 由上述降维算法的思想, 则高维函数 $\begin{matrix} g (x) \end{matrix}$ 的分解可看作是有限和叠加的形式:

$\begin{matrix} \begin{matrix} g (x) = g_{0} + \overset{N}{\sum_{i = 1}} g_{i} (x_{i}) + \sum_{1 \leq i_{1} \leq i_{2} \leq N} g_{i_{1} i_{2}} (x_{i_{1}}, x_{i_{2}}) + \\ \dots + \sum_{1 \leq i_{1} < \dots < i_{S} \leq N} g_{i_{1} i_{2} \dots i_{S}} (x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{S}}) + \dots + \\ g_{12 \dots N} (x_{1}, x_{2}, \dots, x_{N}) \end{matrix} \end{matrix}$ (2)

式中: $\begin{matrix} g_{0} \end{matrix}$ 为常数项; $\begin{matrix} g_{i} (x_{i}) \end{matrix}$ 为输入变量 $\begin{matrix} x_{i} \end{matrix}$ 对于 $\begin{matrix} g (x) \end{matrix}$ 单独作用的一维(单变量)函数; $\begin{matrix} g_{i_{1} i_{2}} (x_{i_{1}}, x_{i_{2}}) \end{matrix}$ 为输入变量 $\begin{matrix} (x_{i_{1}}, x_{i_{2}}) \end{matrix}$ 对于 $\begin{matrix} g (x) \end{matrix}$ 共同作用的二维(双变量)函数; $\begin{matrix} g_{i_{1} i_{2} \dots i_{S}} (x_{i_{1}}, x_{i_{2}}, \dots, x_{i_{S}}) \end{matrix}$ 为变量共同对 $\begin{matrix} g (x) \end{matrix}$ 作用的S个变量函数; g_(1, 2, …, N) (x_1, x_2, …, x_N)为所有变量共同对g(x)的影响。

由式(2)得单变量( $\begin{matrix} S = 1 \end{matrix}$ )降维表达式为:

$\begin{matrix} \begin{matrix} {\hat{g}}_{1} (x) = {\hat{g}}_{1} (x_{1}, \dots, x_{N}) = \overset{N}{\sum_{i = 1}} g (μ_{1}^{*}, \dots, \\ μ_{i - 1}^{*}, x_{i}, μ_{i + 1}^{*}, \dots, μ_{N}^{*}) - (N - 1) g (μ^{*}) \end{matrix} \end{matrix}$ (3)

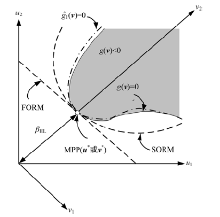
图1给出了在MPP点处极限状态面的一次二阶矩法(FORM)和二次二阶矩法(SORM)及本文方法 $\begin{matrix} S = 1 \end{matrix}$ 时的近似情况。从图1可知, 与其他方法比, 本文方法与实际功能函数的拟合度较好。

	Figure Option View Download New Window
	图1 当S=1, N=2时的功能函数的近似Fig.1 Approximation of performance function when S=1, N=2

2 泰勒级数

在得到高维函数的近似降维表达式后, 为拟合功能函数的累积密度函数, 就需要计算其统计矩。文献[14]利用了点估计来计算随机结构响应统计矩, 该方法通常只用到随机变量的前三阶矩信息, 改进后虽能用到第四阶矩, 但计算精度仍得不到保证。因而, 本文借助于泰勒级数展开理论, 将泰勒级数展开并取至二次项。假设结构的功能函数为 $\begin{matrix} Z = g (x), \end{matrix}$ 其中 $\begin{matrix} x = [x_{1}, x_{2}, \dots, x_{N}]^{T} \end{matrix}$ 中 $\begin{matrix} x_{i} \end{matrix}$ 的前四阶中心矩分别为 $\begin{matrix} μ_{x_{i 1}} 、 μ_{x_{i 2}} 、 μ_{x_{i 3}} \end{matrix}$ 和 $\begin{matrix} μ_{x_{i 4}} 。 \end{matrix}$

功能函数 $\begin{matrix} Z \end{matrix}$ 的前四中心阶矩表达式如下:

功能函数的一阶矩(均值)表达式为:

$\begin{matrix} μ_{Z_{1}} = {\hat{g}}_{1} (μ_{x}) + \frac{1}{2} \overset{N}{\sum_{i = 1}} \frac{\partial^{2} {\hat{g}}_{1} (μ_{x})}{\partial x_{i}^{2}} μ_{x_{i_{2}}} \end{matrix}$ (4)

功能函数的二阶中心矩(方差)表达式为:

$\begin{matrix} \begin{matrix} μ_{Z_{2}} = σ_{Z}^{2} = E [(Z - μ_{Z_{1}})^{2}] = \\ \overset{N}{\sum_{i = 1}} {[\frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}}]}^{2} μ_{x_{i_{2}}} + \overset{N}{\sum_{i = 1}} \frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}} \frac{\partial^{2} {\hat{g}}_{1} (μ_{x})}{\partial x_{i}^{2}} μ_{x_{i_{3}}} + \\ \frac{1}{4} \overset{N}{\sum_{i = 1}} {[\frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}}]}^{2} (μ_{x_{i_{4}}} - 3 μ_{x_{i_{2}}}^{2}) + \\ \frac{1}{2} \overset{N}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} {[\frac{\partial^{2} {\hat{g}}_{1} (μ_{x})}{\partial x_{i} \partial x_{j}}]}^{2} μ_{x_{i_{2}}} μ_{x_{j_{2}}} \end{matrix} \end{matrix}$ (5)

功能函数的三阶中心矩(偏度)表达式为:

$\begin{matrix} \begin{matrix} μ_{Z_{3}} = \overset{N}{\sum_{i = 1}} {[\frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}}]}^{3} μ_{x_{i_{3}}} + \\ \frac{3}{2} \overset{N}{\sum_{i = 1}} {[\frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}}]}^{2} \frac{\partial^{2} {\hat{g}}_{1} (μ_{x})}{\partial x_{i}^{2}} \times (μ_{x_{i_{4}}} - 3 μ_{x_{i_{2}}}^{2}) + \\ 3 \overset{N}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} \frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}} \times \frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{j}} \frac{\partial^{2} {\hat{g}}_{1} (μ_{x})}{\partial x_{i} \partial x_{j}} μ_{x_{i_{2}}} μ_{x_{j_{2}}} \end{matrix} \end{matrix}$ (6)

功能函数的四阶中心矩(峰度)表达式为:

$\begin{matrix} \begin{matrix} μ_{Z_{4}} = \overset{N}{\sum_{i = 1}} {[\frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}}]}^{4} (μ_{x_{i_{4}}} - 3 μ_{x_{i_{2}}}^{2}) + \\ 3 \overset{N}{\sum_{i = 1}} \overset{N}{\sum_{j = 1}} {[\frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{i}}]}^{2} {[\frac{\partial {\hat{g}}_{1} (μ_{x})}{\partial x_{j}}]}^{2} μ_{x_{i_{2}}} μ_{x_{j_{2}}} \end{matrix} \end{matrix}$ (7)

3 Edgeworth级数

得到功能函数的前四阶中心矩后, 再拟合结构功能函数的累积分布函数。相应的求解方法有:Pearson系统^{[15, 16]}、广义Lambda分布^{[17, 18]}、鞍点近似法^{[19, 20, 21]}及最大熵方法^{[22, 23]}等。上述方法因其简单且高效而应用范围颇为广泛, 但当函数非线性程度较高、变异系数较大等因素存在时, 计算精度均不够理想; 而Edgeworth级数仅需利用矩信息便可拟合功能函数的累积分布函数且推导公式简单易获得。因而, 本文利用Edgeworth级数展开法拟合功能函数的累积分布函数和概率密度函数, 最终结合可靠性理论计算得到结构的失效概率。拟合的结构功能函数的累积分布函数和概率密度函数的表达式分别为:

$F (g (x)) = Φ (\bar{g}) - \frac{1}{3!} \frac{μ_{Z_{3}}}{\sqrt[]{μ_{Z_{3}}}} Φ^{(3)} (\bar{g}) + \frac{1}{4!} (\frac{μ_{Z_{4}}}{\sqrt[]{μ_{Z_{4}}}} - 3) Φ^{(4)} (\bar{g}) + \frac{10}{6!} {(\frac{μ_{Z_{3}}}{\sqrt[]{μ_{Z_{3}}}})}^{2} Φ^{(6)} (\bar{g}) + \dots$ (8)

$f (g (x)) = φ (\bar{g}) - \frac{1}{3!} \frac{μ_{Z_{3}}}{\sqrt[]{μ_{Z_{3}}}} φ^{(3)} (\bar{g}) + \frac{1}{4!} (\frac{μ_{Z_{4}}}{\sqrt[]{μ_{Z_{4}}}} - 3) φ^{(4)} (\bar{g}) + \frac{10}{6!} {(\frac{μ_{Z_{3}}}{\sqrt[]{μ_{Z_{3}}}})}^{2} φ^{(6)} (\bar{g}) + \dots$ (9)

式中: $\begin{matrix} \bar{g} \end{matrix}$ 为已标准化的功能函数; $\begin{matrix} Φ (\bar{g}) 、 Φ^{(i)} (\bar{g}) \end{matrix}$ 分别为标准正态分布函数及其 $\begin{matrix} i \end{matrix}$ 阶偏导函数; $\begin{matrix} φ (\bar{g}) 、 φ^{(i)} (\bar{g}) \end{matrix}$ 分别为标准正态分布的概率密度函数及其 $\begin{matrix} i \end{matrix}$ 阶偏导函数。

因此, 可应用Edgeworth级数方法避免对结构功能函数各变量的分布类型的限制, 且仅需要展开至其前四阶项即可, 仅通过统计矩信息即可拟合功能函数的累积分布函数和概率密度函数, 推导简单易行, 扩大了工程实际中的应用范围。

4 数值算例

算例1 考虑一个乘积形式的非线性功能函数 $\begin{matrix} g (x_{1}, x_{2}, x_{3}), \end{matrix}$ 3个随机变量相互独立, 计算其失效概率。随机变量统计参数见表1。功能函数为:

$\begin{matrix} g (x_{1}, x_{2}, x_{3}) = 20 - (x_{1} x_{2}) / x_{3} \end{matrix}$ (10)

表1 基本随机变量统计特征值 Table 1 Statistical characteristics of basic random variables

随机变量	均值	标准差	分布类型
$\begin{matrix} x_{1} \end{matrix}$	10	2.0	对数正态
$\begin{matrix} x_{2} \end{matrix}$	10	1.5	正态
$\begin{matrix} x_{3} \end{matrix}$	10	1.5	极值Ⅰ 型

表1 基本随机变量统计特征值 Table 1 Statistical characteristics of basic random variables

工程中MCS方法的计算结果普遍被认为是精确解。本文方法计算结果与MCS方法的结果基本保持一致, 本文方法的失效概率相对误差仅为1.82%, 且在耗时方面也优于MCS方法(23.3118 s)、FORM方法(3.1381 s)、SORM方法(3.6962 s)。通过表2列举了采用其他几种方法的计算结果与耗时, 说明了本文方法在计算精度和效率上有一定的优势, 具有较好的适应性。

表2 算例1的失效概率计算结果 Table 2 Failure probability calculation results for example 1

算例2 基于材料的蠕变和疲劳试验数据^[24], 在线性损伤积累准则基础上建立了非线性蠕变疲劳失效模型, 所定义的功能函数为:

$\begin{matrix} g = 2 - e^{θ_{1} D_{c}} + \frac{e^{θ_{1}} - 2}{e^{- θ_{2}} - 1} (e^{- θ_{2} D_{c}} - 1) - D_{f} \end{matrix}$ (11)

式中: $\begin{matrix} θ_{1} \end{matrix}$ 和 $\begin{matrix} θ_{2} \end{matrix}$ 为从试验数据中得到的两个参数; $\begin{matrix} N_{c} \end{matrix}$ 与 $\begin{matrix} N_{f} \end{matrix}$ 分别为蠕变和疲劳寿命; $\begin{matrix} n_{c} \end{matrix}$ 和 $\begin{matrix} n_{f} \end{matrix}$ 分别为蠕变和疲劳载荷作用循环数; $\begin{matrix} D_{c} = n_{c} / N_{c}, D_{f} = n_{f} / N_{f} 。 \end{matrix}$ 基本随机变量分布参数见表3。

表3 基本随机变量统计特征值 Table 3 Statistical characteristics of basic random variables

变量	均值	变异系数	分布类型
$\begin{matrix} N_{c} \end{matrix}$	5490	0.2	对数正态
$\begin{matrix} N_{f} \end{matrix}$	17100	0.2	对数正态
$\begin{matrix} n_{c} \end{matrix}$	549	0.2	对数正态
$\begin{matrix} n_{f} \end{matrix}$	4000	0.2	对数正态
$\begin{matrix} θ_{1} \end{matrix}$	0.42	0.2	正态
$\begin{matrix} θ_{2} \end{matrix}$	60	0.2	正态

表3 基本随机变量统计特征值 Table 3 Statistical characteristics of basic random variables

由表4的结果可知, 本文方法的新型可靠度计算方法在计算精度上都远远好于传统的FORM方法和SORM方法; MCS方法的模拟次数为10⁶次, 而本文方法无需迭代求解, 无需多重积分, 无需求解功能函数的逆矩阵, 仅需要少量的确定性计算即可, 与其相比用很少的计算成本得到与其相近的计算精度, 体现了本文方法在计算精度上具有一定的优越性。

表4 算例2的失效概率计算结果 Table 4 Failure probability calculation results for example 2

算例3 如图2所示的屋架, 屋架的上弦杆和其他压杆采用钢筋混凝土杆^[12], 下弦杆和其他拉杆采用钢杆。屋架承受均布载荷 $\begin{matrix} q \end{matrix}$ 作用(见图2(a)), 将均布载荷 $\begin{matrix} q \end{matrix}$ 化成节点荷载后有 $\begin{matrix} P = (qL \frac{)}{4} \end{matrix}$ (见图2(b))。设 $\begin{matrix} A_{S} 、 A_{C} 、 E_{S} 、 E_{C} \end{matrix}$ 分别为混凝土和钢杆的横截面积、弹性模量, $\begin{matrix} L \end{matrix}$ 为钢杆长度。A_S=9.82× 10^-4m², A_C=0.04 m²。分布参数见表5。

	Figure Option View Download New Window
	图2 屋架结构示意图Fig.2 Roof truss structure diagram

表5 基本随机变量统计特征值 Table 5 Statistical characteristics of random variable value

考虑屋架的合理性, 以屋架顶端 $\begin{matrix} C \end{matrix}$ 点的向下挠度不大于0.019 m为约束条件。根据约束条件可得到结构功能函数为:

$\begin{matrix} g = 0.019 - Δc \end{matrix}$ (12)

计算结果如表6所示, 本文方法的计算结果与MCS方法的相对误差仅为4.3‰ , 且耗时仅为其0.34倍, 进一步表明了本文方法在计算精度方面具有一定的优越性, 同时也体现了本文方法的合理性与适应性。

表6 算例3的失效概率计算结果 Table 6 Results of probability of failure for example 3

5 结束语

本文将降维算法与泰勒级数及Edgeworth级数法相结合, 提出了一种新型的直接计算结构可靠性分析方法。采用该方法针对功能函数为高维非线性的复杂结构进行计算分析。结果表明:采用本文方法求解的结果同MCS方法求解的结果基本保持一致, 大大节省了计算工作量, 且在耗时方面也具由一定的优势; 本文方法无需进行复杂的多重积分求解结构功能函数的统计矩, 无需求解结构功能函数的逆矩阵, 使得计算工作量大大减小。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张鹏军, 王惠源, 李强, 等. 弹药精确装填可靠性分析及测试[J]. 光学精密工程, 2014, 22(7): 1787-1793. Zhang Peng-jun, Wang Hui-yuan, Li Qiang, et al. Analysis and test of reliability for ammunition accurate ramming[J]. Optics and Precision Engineering, 2014, 22(7): 1787-1793. [本文引用:1]
[2]	陈传海, 杨兆军, 孟广伟, 等. 考虑多种误差影响的数控机床载荷谱编制[J]. 光学精密工程, 2015, 23(10z): 355-360. Chen Chuan-hai, Yang Zhao-jun, Meng Guang-wei, et al. Load spectra of NC machine tools considering multiple influence factors[J]. Optics and Precision Engineering, 2015, 23(10z): 355-360. [本文引用:1]
[3]	Tang X S, Li D Q, Zhou C B, et al. Copula-based approaches for evaluating slope reliability under incomplete probability information[J]. Structural Safety, 2015, 52: 90-99. [本文引用:1]
[4]	Balu A S, Rao B N. Multicut-High Dimensional Model Representation for Reliability Bounds Estimation[M]. New York: Springer International Publishing, 2015: 499-510. [本文引用:1]
[5]	周志国, 卢江跃. 弯曲振动下压电陶瓷复合圆盘的可靠性分析[J]. 吉林大学学报: 工学版, 2013, 43(增刊1): 138-142. Zhou Zhi-guo, Lu Jiang-yue. Reliability analysis of piezoceramics composite plate under bending vibration model[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(Sup. 1): 138-142. [本文引用:1]
[6]	王保群, 张强勇, 李术才, 等. 盐岩地下储气库体积收敛失效概率分析与模型试验验证[J]. 吉林大学学报: 地球科学版, 2014, 44(3): 954-960. Wang Bao-qun, Zhang Qiang-yong, Li Shu-cai, et al. Analysis of failure probability and verification of model test underground uas storage's volume convergence in salt rock[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(3): 954-960. [本文引用:1]
[7]	Alibrand i U, Alani A M, Ricciardi G. A new sampling strategy for SVM-based response surface for structural reliability analysis[J]. Probabilistic Engineering Mechanics, 2015, 41: 1-12. [本文引用:1]
[8]	Arastu M, Datta T K. Reliability analysis using genetic algorithm under seismic load[J]. Research Journal of Science and Technology, 2015, 7(1): 9-13. [本文引用:1]
[9]	Dai H, Zhang H, Wang W. A multiwavelet neural network‐based response surface method for structural reliability analysis[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(2): 151-162. [本文引用:1]
[10]	Rahman S, Wei D. A univariate approximation at most probable point for higher-order reliability analysis[J]. International Journal of Solids and Structures, 2006, 43(9): 2820-2839. [本文引用:1]
[11]	Kong C, Sun Z, Niu X, et al. Moment methods for C/SiC woven composite components reliability and sensitivity analysis[J]. Science and Engineering of Composite Materials, 2014, 21(1): 121-128. [本文引用:1]
[12]	Vrbik J. Moments of AR( k) parameter estimators[J]. Communications in Statistics-Simulation and Computation, 2014, 44(5): 1239-1252. [本文引用:2]
[13]	Rivlin Y, Pinchas M. Edgeworth expansion based model for the convolutional noise pdf[J]. Mathematical Problems in Engineering, 2014, 2014(4): 1-19. [本文引用:1]
[14]	Kah D, Emre O, Tran Q H, et al. High order moment method for polydisperse evaporating sprays with mesh movement: application to internal combustion engines[J]. International Journal of Multiphase Flow, 2015, 71: 38-65. [本文引用:1]
[15]	Pearson P B. The impact of school-level factors on minority students' performance in AP calculus[D]. Warsaw: Portland State University, 2014. [本文引用:1]
[16]	Kim S D, Hammond R K, Bickel J E. Improved mean and variance estimating formulas for PERT analyses[J]. IEEE Transactions on Engineering Management, 2014, 61(2): 362-369. [本文引用:1]
[17]	Abelev B, Adam J, Adamová D, et al. Multiplicity dependence of pion, kaon, proton and lambda production in p-Pb collisions at s NN = 5. 02 TeV mathContainer Loading Mathjax[J]. Physics Letters B, 2014, 728(1): 25-38. [本文引用:1]
[18]	Ristić M, Kundu D. Marshall-Olkin generalized exponential distribution[J]. Metron, 2015, 73(3): 1-17. [本文引用:1]
[19]	Duncan J, Wu Q, Promislow K, et al. Biased gradient squared descent saddle point finding method[J]. Journal of Chemical Physics, 2014, 140(19): 194102. [本文引用:1]
[20]	Plasencia M, Pedersen A, Arnaldsson A, et al. Geothermal model calibration using a global minimization algorithm based on finding saddle points and minima of the objective function[J]. Computers & Geosciences, 2014, 65: 110-117. [本文引用:1]
[21]	Chao Z, Chen G. A note on semi-convergence of generalized parameterized inexact Uzawa method for singular saddle point problems[J]. Numerical Algorithms, 2015, 68(1): 95-105. [本文引用:1]
[22]	Shi X, Teixeira A P, Zhang J, et al. Structural reliability analysis based on probabilistic response modelling using the maximum entropy method[J]. Engineering Structures, 2014, 70(9): 106-116. [本文引用:1]
[23]	Peco C, Millán D, Rosolen A, et al. Efficient implementation of Galerkin meshfree methods for large-scale problems with an emphasis on maximum entropy approximants[J]. Computers & Structures, 2015, 150: 52-62. [本文引用:1]
[24]	宋述芳, 吕震宙. 基于鞍点估计及其改进法的可靠性灵敏度分析[J]. 力学学报, 2011, 43(1): 162-168. Song Shu-fang, Lyu Zhen-zhou. The reliability sensitivity analysis based on saddlepoint approximation and its improved method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 162-168. [本文引用:1]

2014

0.0

. 2014, 22(7):1787-1793 DOI:doi:10.3788/OPE.20142207.1787

Analysis and test of reliability for ammunition accurate ramming

弹药精确装填可靠性分析及测试

Zhang Peng-jun , Wang Hui-yuan , Li Qiang

张鹏军, 王惠源, 李强

为了保证在复杂环境下连续工作的火炮自动装填机构装填参数的一致性,研究了火炮自动装填机构工作的可靠性及其测试方法.首先,分析了装填参数变化对内弹道参数的影响和导致参数变化的原因.然后,设计了多传感器装填参数测试系统,利用该系统对输弹过程和输弹效果进行了综合测试.测试结果表明:在装填开始60 ms左右装填机构尾部出现的峰峰值为14 mm的振动是影响弹丸入膛姿态并与身管尾端面碰撞的主要原因;当弹丸的挤入压力为3 300～14 000 N时,卡膛行程在2 mm内变化;根据密集度分布将卡膛行程分为三个区域,其中第二区域1.321～1.557mm为可靠卡膛区.测试表明,所采用测试方法和精度能够满足装填机构的检测要求,可为装填机构的结构优化和性能评估提供数据支撑.

... 在工程实际中,经常会遇到大量功能函数为高维非线性的复杂结构问题,要考虑结构的不确定性变量和结构设计的安全性,因而可用可靠度方法来解决此类问题^[1,2] ...

2015

0.0

2015

0.0

... 对于可靠度分析的常见方法有解析法^[3,4]、梯度法^[5,6,7]和数值模拟法^[8,9]等 ...

2015

0.0

... 对于可靠度分析的常见方法有解析法^[3,4]、梯度法^[5,6,7]和数值模拟法^[8,9]等 ...

2013

0.0

. 2013, 43(增刊1):138-142

Reliability analysis of piezoceramics composite plate under bending vibration model

弯曲振动下压电陶瓷复合圆盘的可靠性分析

Zhou Zhi-guo , Lu Jiang-yue.

周志国, 卢江跃

In order to speed up the process of the orthogonal test for determining structure parameters of piezoceramics composite plate.Based on the Monte Carlo methods of reliability analysis,the determination of parameters of piezoceramics composite under the bending vibration model in the piezoelectric nozzles-flapper structure was studied.The probability design system in the ANSYS software was applied to calculate the impact of the non-deterministic input parameters on the structural properties.The ANSYS analysis results show that the largest sensitivity on the nozzle-flapper structure is the radius R -1 of piezoelectric ceramic and then followed by the copper electrode thickness T -2 .The both impacts are negative.It indicates that they have the inverse relation to the structural properties of the nozzle-flapper.While the influence of the thickness T -1 of the piezoelectric ceramic is positive.It indicates that it has the proportional relation to the nozzle-flapper performance.And the quantitative relationship among the three parameters is R -1 > T -2 > T -1 .The study results provide a basis for speeding up the process of the orthogonal test and improving test accuracy.

为加快压电陶瓷复合圆盘结构参数的确定中所做的正交试验进程,研究了基于可靠性分析的Monte Carlo法,对压电喷嘴-挡板结构中盘弯曲振动下的压电陶瓷复合圆盘参数进行选定,利用ANSYS软件的概率设计系统分析非确定性输入参数对结构性能的影响。分析结果表明,喷嘴-挡板结构对压电陶瓷半径 R -1 敏感性最大,其次为铜电极厚度 T -2 ,二者影响均为负值,说明它们与喷嘴-挡板的结构性能成反比,而压电陶瓷厚度 T -1 影响是正值,表明它与喷嘴-挡板结构性能成正比,并且得出三者之间定量关系为 R -1 > T -2 > T -1 。研究结果为加快正交试验进程,提高试验准确性提供了依据。

... 对于可靠度分析的常见方法有解析法^[3,4]、梯度法^[5,6,7]和数值模拟法^[8,9]等 ...

2014

0.0

. 2014, 44(3):954-960 DOI:doi:10.13278/j.cnki.jjuese.201403205

Analysis of failure probability and verification of model test underground uas storage's volume convergence in salt rock

盐岩地下储气库体积收敛失效概率分析与模型试验验证

Wang Bao-qun , Zhang Qiang-yong , Li Shu-cai

王保群, 张强勇, 李术才

Because of the creep characteristics of salt rock, underground gas storage in salt rock will produce larger shrinkage deformation and affect its safe and stable operation. There is no unified national standard for analysis methods and evaluation criteria for gas storage cavity stability currently. The numerical simulation is mainly adopted to evaluate gas storage cavity stability in China. Based on numerical simulation on shrinkage deformation of underground gas storage in Jintan salt mine and using foreign evaluation criteria for underground gas storage stability in salt for reference, volume convergence failure risk evaluation matrix of underground gas storage in salt rock has been established. And the analysis and displaying performance function of volume convergence failure probability of gas storage has been established with first-order second-moment method. The results indicated that failure probability of volume convergence decreases with increasing of internal pressure under long-term constant internal pressure, while it increases with decrease of internal pressure under peak shaving short-term lower internal pressure and the minimum internal pressure should be kept at more than 4.2 MPa. By large scale three-dimensional geomechanical model test on underground gas storage in bedded salt rock under condition of alternating gas pressure, volume convergence deformation of gas storage decreases with increasing of internal pressure and the minimum internal pressure during short-term operation should be greater than 4.0 MPa. The results of model test and failure probability analysis are more similar. So, the minimum internal pressure in peak shaving shortterm should be over 4.0 MPa in order to avoid volume convergence failure for underground gas storage in salt rock.

盐岩地下储气库受盐岩蠕变特性影响会产生较大的体积收缩变形，影响储气库安全稳定运行。目前对地下储气库体积稳定性分析方法和评价准则各国没有统一标准，国内主要采用数值计算的方法来评价储气库体积稳定性。以江苏金坛盐矿地下储气库体积收敛数值分析为基础，借鉴国外盐岩地下储气库稳定性评价标准，建立盐岩地下储气库体积收敛失效风险评价矩阵，采用一次二阶矩法显示功能函数分析储气库体积收敛失效概率，分析得出：储气库在长期恒定内压工况下体积收敛失效概率随内压的增大而减小;在短期调峰低压工况下体积收敛失效概率随内压的减小而增大;最小内压应保持在4.2 MPa以上。通过交变气压条件下层状盐岩地下储气库大型三维地质力学模型试验得出:储气库体积收敛变形随内压的增大而减小;短期运行最小内压应大于4.0 MPa。模型试验结果与失效概率分析结论较为相似。因此，为避免盐岩地下储气库产生体积收敛破坏，应保证调峰短期最小内压在4.0 MPa以上。

... 对于可靠度分析的常见方法有解析法^[3,4]、梯度法^[5,6,7]和数值模拟法^[8,9]等 ...

2015

0.0

... 对于可靠度分析的常见方法有解析法^[3,4]、梯度法^[5,6,7]和数值模拟法^[8,9]等 ...

2015

0.0

... 对于可靠度分析的常见方法有解析法^[3,4]、梯度法^[5,6,7]和数值模拟法^[8,9]等 ...

2015

0.0

... 对于可靠度分析的常见方法有解析法^[3,4]、梯度法^[5,6,7]和数值模拟法^[8,9]等 ...

2006

0.0

... 因此,本文提出一种基于降维算法^[10]的直接结构可靠性分析方法 ...

2014

0.0

... 运用降维思想,利用 n个一维函数近似表达高维函数,构造成新的函数模型,借助于泰勒级数展开法与统计矩理论,通过计算获得结构功能函数的前四阶中心矩,再运用Edgeworth^[11,12,13]级数法,可拟合结构功能函数的累积分布函数和概率密度函数,最后结合可靠性理论计算得到结构的失效概率 ...

2014

0.0

... 算例3 如图2所示的屋架,屋架的上弦杆和其他压杆采用钢筋混凝土杆^[12],下弦杆和其他拉杆采用钢杆 ...

2014

0.0

2015

0.0

2014

0.0