纤维增强复合材料板由不同铺层角度的纤维在基体材料中层叠而成^[1], 具有比强度高、比模量大的特点, 能够满足某些特殊的性能需求。材料中纤维断裂损伤对其性能有很大影响, 因此需要对这一类损伤进行检测, 超声无损检测^[2]无疑是现有的重要检测技术之一。深入认识复合材料板中导波的传播特性是应用超声检测的前提, 在这一领域前人做了大量的工作, 也取得了重要进展和成果。孙丹^[3]研究了功能梯度复合材料板中波的传播特性和冲击响应问题。Lee^[4]提出了一种波在多向复合材料板中的传播解析模型, 通过对此模型中波传播问题的研究, 发现了不同材料对频散特征的影响很大。Liu等^{[5, 6]}通过数值方法得到了各向异性层合板中波的传播频散特征, 并详细分析了不同传播模态的相速度。Nishiwaki等^[7]结合有限元方法与实验方法研究了复合材料层合板中弹性波的传播。Jeong等^{[8, 9]}采用小波转换法分析了复合材料板中波的传播特性。Datta等^[10]则在得到任意层数复合材料层板中波的传播特性后, 发现复合材料层合板和单层板中的频谱是不同的。Kudela等^[11]采用谱元法研究了横向弹性波在复合材料中的传播, Lima和Braga^[12]用递归算法得到了Lamb波的频谱。带状单元法是一种被用来分析层状结构的数值计算方法, 具有求解效率高、计算稳定性好的特点。Liu等^[13]用此方法分析了波在含裂纹各向异性层合板中的散射。陈江义等^[14]则用该方法研究了任意梯度分布板中的导波频散特性。

在此基础上, 本文利用带状单元法来研究复合材料板中不同铺层纤维断裂损伤对导波频散特性的影响, 以期对这些影响有更深入的认识, 并能为复合材料板中这类损伤的检测提供理论参考。

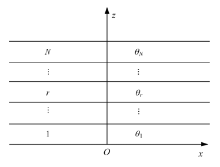
图1为N层纤维增强复合材料板, 厚度沿z轴方向, 各铺层与xoy平面平行, 铺层角为θ , x轴与0° 铺层的纤维方向相同。由于每层纤维的铺层角不同, 因此各层的材料弹性常数也不相同。在此, 将0° 铺层的材料弹性常数矩阵用C^0 表示, 即 C0=c110c1300c130c330000c550, 其它铺层角所对应的材料弹性常数可由对C⁰进行变换得到。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 复合材料板Fig.1 Composite plate model

变换方法如下:

将0° 铺层的材料弹性常数矩阵用四阶张量表示为 Cijkl0(i, j, k, l=1, 2, 3), 下标1、2和3分别代表笛卡尔坐标系中x、y和z轴。根据变换关系, 其他铺层材料的弹性常数可表达为^[15]:

Cmnop(r)=βmiβnjβokβplCijkl0(1)

式中:下角m, n, o, p=1, 2, 3; β 为二阶张量, 描述了任意铺层弹性常数相对于0° 铺层的变换关系, 对于角度为 θr的铺层, 变换关系表达成矩阵形式为:

β= cosθrsinθr0-sinθrcosθr0001(2)

由式(1)和(2)即可求得 θr角度铺层的材料弹性常数。

如果板中某个铺层(比如第 i层)发生纤维断裂损伤, 则弹性常数退化成与基体材料的弹性常数相同, 即:

C(i)=Cb(3)

式中: Cb为基体材料的弹性常数矩阵。

假设板在x和y方向无限大, 考虑导波沿 x方向传播。在不考虑体力的情况下, 根据哈密尔顿原理, 其拉格朗日函数的变分满足:

δ∫t1t2Ldt=0(4)

其中拉格朗日函数L=T-E。对于第r层, 其动能 T(r)可表示为:

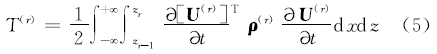
式中:z_r 、z_r-1 分别为第r层的上、下表面的z坐标; U^(r)为位移向量; ρ(r)=ρr00ρr为密度矩阵, 介质的势能 E(r)可表示为:

式中:ε ^(r)为应变向量, 将第r层的弹性常数矩阵C^(r)带入式(6)中, 再利用带状单元法对位移进行插值, 从而改写式(5)和(6)后, 代入式(4)中即可以得到用节点位移表示的第r层简化运动方程^[14]:

K1(r)s(r)+K2(r)s, x(r)-K3(r)s, xx(r)+M(r)s··(r)=0(7)

式中: K1(r)和 K3(r)为对称矩阵; K2(r)为反对称矩阵。

对于一个复合材料板, 其运动方程可由各层运动方程组装而成, 组装方法类似于有限元方法。此外, 假设复合材料板上、下表面应力自由, 此时板表面的应力可表示力:

σ=0(8)

引入边界条件(8)后, 最后可以得到板的总体运动方程:

K1s+K2s, x-K3s, xx+Ms··=0(9)

假设式(9)的解为 s=s0ei(kx+ωt),其中 i=-1, k为波数, ω为频率, 因此可以得到板中导波传播时的特征值问题:

K1-ω2M+ikK2+k2K3s0=0(10)

要想使式(10)有解, 频率和波数需满足:

0IK1-Mω2K2-ikI00K3=0(11)

式中: I为单位矩阵。式(11)是导波在板中传播的频散方程, 利用该方程可以分析纤维断裂损伤对复合材料板中导波频散特性的影响。

以T300/1034-C碳纤维增强复合材料板为对象研究纤维断裂损伤对导波频散特性的影响。板的铺层形式为[(0° /30° /60° /90° )₂]_s, 共16层, 各铺层厚度均为5 μ m, 0° 铺层和树脂基体的材料弹性常数如表1所示。

表1

Table 1

表1(Table 1)

表1 T300/1034-C复合材料板材料常数 Table 1 Material properties of T300/1034-C composite plate 材料 密度 /(kg· m-3) c11/GPa c13/GPa c33/GPa c55/GPa 0° 铺层 1500 213.0 8.54 18.23 5.78 树脂基体 1500 1.87 1.15 1.87 0.36

表1 T300/1034-C复合材料板材料常数 Table 1 Material properties of T300/1034-C composite plate

为了全面研究纤维断裂损伤对板中导波频散特性的影响, 在设计算例时考虑多种损伤模式, 主要分单层纤维断裂和多层纤维断裂两大类。在分析单层纤维断裂时, 还要考虑不同铺层角和不同位置层的损伤模式。在分析多层断裂时, 进一步考查连续多层纤维断裂和离散多层纤维断裂等不同的损伤模式。

2.1 单层纤维断裂损伤

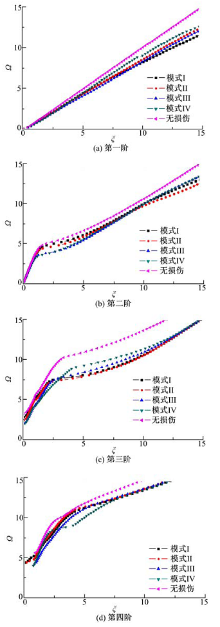
对于单层纤维断裂损伤, 这里具体定义4种损伤模式:第2层纤维断裂(θ ₂=30° , 简称“ 模式Ⅰ ” ); 第3层纤维断裂(θ ₃=60° , 模式Ⅱ ); 第5层纤维断裂(θ ₅=0° , 模式Ⅲ ); 第6层纤维断裂(θ ₆=30° , 模式Ⅳ )。图2给出了上述损伤模式下以及无损伤板的前四阶频散曲线, 图中横坐标为无量纲波数 ξ=kh(h为板厚), 纵坐标为无量纲频率 Ω=ωh/c550/ρ。

从图2中可知:①由于纤维断裂损伤导致结构刚度下降, 因此在同波数下, 与无损伤板相比, 含损伤板中导波的频率值

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 单层损伤板中频散曲线Fig.2 Dispersion curves in plate with single damaged layer

有所降低; ②在较低的频段, 4种单层纤维断裂损伤模式对导波频散特性的影响并不明显, 这种影响在高频段才能表现出来; ③相较无损伤复合材料板, 4种损伤模式都会改变导波的频散特性, 但不同损伤模式的影响区别不大; ④由于这里假设导波沿 x方向传播, 因此理论上0° 铺层的纤维断裂对板中导波传播的影响最大, 但从图中可以看出:损伤模式I对第一阶频散特性的影响最大, 损伤模式II对第二阶频散特性的影响最大, 所以影响频散特性的不只有铺层角, 还有各铺层到板表面的距离; ⑤随着阶次增高, 各损伤模式对频散特性的影响难以分辨(如第四阶), 因此不宜通过导波高阶模态的变化来对单层纤维断裂损伤的复合材料进行检测。

2.2 多层纤维断裂损伤

对于多层纤维断裂损伤, 这里假设3种损伤模式:

(1)模式Ⅴ :第6层(θ ₆=30° )、第7层(θ ₇=60° )、第8层(θ ₈=90° )连续三层纤维断裂。

(2)模式Ⅵ :第2层(θ ₂=30° )、第10层(θ ₁₀=60° )、第13层(θ ₁₃=90° )纤维断裂损伤, 三层不连续。

(3)模式Ⅶ :第6层(θ ₆=30° )、第11层(θ ₁₁=30° )、第15层(θ ₁₅=30° )纤维断裂损伤, 三层铺层角相同, 但不连续。

图3对上述3种损伤模式、单层损伤模式Ⅰ 及无损伤板中的前四阶频散曲线进行了对比。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 三层损伤板中频散曲线Fig.3 Dispersion curves in plate with three damaged layers

相较单层纤维断裂损伤, 多层纤维断裂损伤模式对导波频散特性的影响有一些特点。由图3可以看出:①多层损伤模式对导波传播的影响要大于单层损伤, 这也是显而易见的; ②同样三个铺层出现纤维断裂损伤, 但连续层损伤对导波频散特性的影响要大于离散层损伤; ③对于非连续层损伤模式Ⅵ 和Ⅶ , 尽管它们的铺层角不同, 而且各层的位置也不同, 但是对频散特性的影响基本相似, 因此用超声导波或许可以检测出多层损伤, 但具体判断损伤所在的层位置可能会比较困难。

(1)基于带状单元模型, 给出了分析含纤维断裂损伤复合材料板中导波频散特性的方法。首先利用坐标变换方法计算了各铺层的材料常数, 并假设纤维断裂的铺层材料常数与树脂基体相同。然后利用带状单元法和哈密尔顿原理推导出反映导波频散特性的特征值问题。

(2)考查了不同情况下的单层纤维断裂损伤和多层纤维断裂损伤对导波传播特性的影响。单层损伤时, 只有在高频段时损伤对频散特性的影响较大, 此时影响频散特性的还有铺层角及铺层到板表面距离。多层损伤对频散特性的影响要大于单层损伤, 尤其是连续的多层损伤。