多点拉弯成形的核心原理是将传统的整体拉弯成形模具离散成一系列规则排列、形状可调的基本体(或称模具头体), 各基本体的位置可独立地调节, 改变各基本体的位置就改变了成形曲面, 也就相当于重新构造了成形模具, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 传统拉弯成形与多点拉弯成形Fig.1 Traditional stretch-bending and multi point stretch-bending

型材的三维拉弯成形是将型材水平和垂直方向上分别形成不同几何形状的成形过程。由于增加了型材垂直方向的弯曲成形, 因此多点拉弯三维成形工艺较传统工艺更为复杂, 成形过程主要如下所示。

(1)调形。首先应调整多点离散化成形模具的各个柔性单元体位置参数, 使其包络面构成目标成形零件的几何形状。

(2)预拉伸。在轴向拉力的作用下, 型材被预先拉伸至塑性状态, 预拉伸可以有效地减小成形件的回弹变形。

(3)扭转。在贴合模具前, 进行适当的扭转变形, 可以有效地提高弯曲件的结构强度, 以满足成形要求。

(4)水平弯曲。型材逐渐贴模, 在水平方向上弯曲成形。

(5)垂直弯曲。垂直方向的液压系统使型材在垂直方向上弯曲成形。

(6)补拉伸。可有效地减小成形件的回弹变形。

(7)卸载。

(8)测量回弹。根据回弹数据对多点离散化成形模具的位置参数进行调整, 再次进行拉弯实验, 直到成形件回弹误差小于规定范围值, 获得符合加工标准的成形零件, 一般在3次之内就可调好。

与其他常用的自由曲面工件成形方法相比, 使用多点调整式柔性模具头体的多点连续拉弯成形方法具有如下技术特点:①生产效率高; ②成形精度高; ③生产环境好; ④能源消耗少; ⑤生产成本低; ⑥实现无模成形; ⑦装备结构比较简单; ⑧易实现自动化。

在柔性拉弯成形有限元分析中, 主要是模拟型材在夹钳作用下逐渐贴合柔性模具的过程。对有限元模型进行如下简化。

(1)模型组成简化。夹钳的控制元件可在模型中将其简化不使用, 通过边界条件对夹钳进行位移控制。柔性成形模具在模型中进行简化, 不使用其控制元件等, 在模型中仅使用模具头体部分的简化模型作为柔性模具, 通过边界条件对其进行位移控制。

(2)模型对称简化。在有限元模拟中, 因型材几何形状对型材的中间截面对称, 为了简化模型和缩短计算时间, 对型材、模具和夹钳都采用二分之一模型。

(3)形状简化。当加工型材的形状不同, 只需更换不同几何形状的夹钳和模具头体, 其它构件均不用更换。为了方便设计, 夹钳形状设计为与型材截面形状相同, 将型材绑定于夹钳。简化后的柔性三维拉弯成形有限元模型如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 柔性三维拉弯成形有限元模型Fig.2 Finite element model for flexible 3D stretch bending forming

显式算法适用于求解准静态问题和复杂的非线性动力学问题, 尤其是瞬时的动态问题。其基于动力学方程, 在时间域中按很短的时间增量来推导出结果, 不需要求解每一个增量步的耦合方程和总刚度矩阵。因此, 该算法不需要迭代, 不存在不收敛的问题。隐式算法适用于线性和非线性问题, 如耦合分析、动态线性、结构静力分析和热分析等问题。该算法是基于虚功原理, 必须进行迭代才能求解非线性问题, 存在不收敛的问题。在每个增量步中要进行多次迭代, 计算总刚度矩阵和总体平衡方程。因此, 占用的内存空间和磁盘空间较大。显式算法和隐式算法都是以施加的载荷外力P、单元内力I和节点加速度定义平衡方程:

Mu··=P-I

式中:u··为节点加速度;M为质量矩阵。

显式算法和隐式算法的主要区别在于采用不同的方法求解节点加速度。显式算法是采用中心差分法, 利用上一个增量步的状态计算下一个增量步的状态。隐式算法采用直接求解法, 即直接求解一组线性方程组。

(1)显式算法。显式算法先对节点进行计算, 在增量步开始时根据式(1), 可以得到加速度为:

u··(t)=M-1(P-I)t(1)

显式算法不需要求解方程组, 任何节点的加速度都完全取决于该节点所受的合力和该节点的质量。用中心差分法对加速度在时间上积分, 假设加速度在速度变化过程中不变, 当前增量步中点的速度为上一个增量步中点的速度加上速度的变化量:

u·(t+Δt/2)=u·(t-Δt/2)+Δt(t+Δt)+Δtt2u··t(2)

根据增量步开始时的位移加上速度对时间的积分计算增量步结束时的位移:

u(t+Δt)=ut+Δt(t+Δt)u·(t+Δt/2)(3)

显示求解算法中, 首先根据增量步开始时的动力平衡方程得到加速度, 然后根据式(3)(4)逐步得到之前的位移和速度。为了使显式求解的结果更加精确, 时间增量步要足够小。节点计算结束后对单元进行计算, 首先根据应变速率计算单元应变增量 dε,然后根据本构方程计算应力:

σ(t+Δt)=f(σ(t), dε)(4)

然后计算集成单元节点内力, 将时间设置为 t+Δt,返回计算节点状态。

(2)隐式算法。隐式算法利用完全Newton迭代求解方法, 通过自动增量步求解问题。隐式算法首先将问题分解为若干个增量步, 每个增量步的解都需要进行迭代计算, 增量步结束后Newton法自动计算满足动力学平衡条件的位移解。每次迭代的瞬时求解方程为:

k^jcj=Pj-Ij-Mju··j(5)

式中: k^j为有效刚度矩阵; c_j为对应位移增量的修正值。

使用隐式算法求解非线性问题时, 每一个增量步都需要进行多次迭代。对于复杂的问题, 使用隐式算法需要占用较多的计算资源, 同时还会占用大量的磁盘空间和内存。

铝型材的柔性拉弯成形工艺的有限元模型分为拉弯成形和回弹两个过程。

(1)拉弯成形过程

型材柔性拉弯成形过程是一个非线性的准静态问题, 成形过程中型材先进行水平弯曲成形, 然后再进行垂直弯曲成形, 而且接触状态不断变化。若采用隐式算法模拟拉弯成形过程, 求解过程过于复杂且耗时较多, 还可能出现收敛问题。用显式算法模拟成形过程, 型材与成形面的接触问题可以更方便地处理, 不用考虑收敛问题, 并且能够更合理地模拟拉弯成形的动态过程。因此, 拉弯成形过程使用动态显式算法进行模拟。使用Abaqus/Explicit对三维拉弯成形进行模拟, 主要参数为加载速度、质量缩放系数和时间等。这些参数需要设置合理的数值, 从而避免因加载速度太快引起的局部变形问题。

(2)回弹过程

柔性拉弯成形回弹研究中, 卸载在模拟过程中占主导地位, 卸载过程中所有接触和外力都不存在, 这使得如果采用隐式算法会容易收敛。若采用动态显式算法研究回弹过程, 虽然不存在收敛问题, 但是即使分析步较小也需要很大的计算量, 与隐式算法相比不具有计算时间短的优势, 而且隐式算法的计算精度高于显式算法。因此, 本文选用静态隐式算法研究回弹过程, 即用Abaqus/Standard模拟回弹过程。

综上所述, 多点柔性拉弯成形有限元模拟过程采用混合算法, 成形过程和回弹过程分别采用不同的算法进行模拟分析, 该方法同时具有显式算法和隐式算法的优点。

型材材料选用铝型材AA6082。形状及尺寸参数如图3所示。其中, B为60 mm, t为8 mm, h为50 mm, b为8 mm, A₁为背板面积, A₂为腹板面积。模拟过程分为柔性三维拉弯成形、节点形状偏差计算和迭代修正模具型面3个阶段。因为模拟过程中型材形状和成形操作对称, 为了减少模拟时间消耗选用柔性拉弯模具和型材的二分之一进行建模。型材拉伸至1000 mm, 模型包括型材、柔性模具和夹钳。模拟中采用预拉量和补拉量为0.75%。每次补拉结束后检测型材参考点与目标坐标偏差大小, 如未达到允许范围, 迭代继续。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 T型材几何形状尺寸Fig.3 Geometry and dimension of T profile

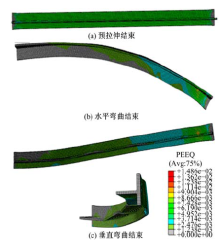
图4为T截面铝型材三维拉弯成形过程中不同时刻的切向主应力状态。图4(a)为预拉伸过程结束后的应力状态, 型材轴向上的应力分布均匀, 应力大小为160 MPa; 图4(b)为水平方向上弯曲成形后的主应力状态; 图4(c)为垂直方向上弯曲成形后的切向主应力状态, 可以看出型材在两个方向上形成了弯曲。由于拉弯成形过程中拉力的作用, 轴向应力一直保持在拉应力的状态下, 且弯曲成形过程中的拉力保持不变, 所以应力状态在弯曲过程中分布仍较为均匀, 弯曲成形结束后应力最大值为205 MPa。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 成形过程中的应力场Fig.4 Stress distribution in forming process

图5为多点拉弯成形过程中不同时刻的等效塑性应变状态。图5(a)为预拉伸结束后的应变分布, 等效塑性应变的大小为0.0042; 图5(b)和5(c)分别为水平方向上、垂直方向上弯曲成形结束后的应变状态。可以看出, 水平弯曲结束后, 应变沿截面方向的大小发生了变化, 靠近内侧的腹板上应变相应的减小, 垂直弯曲结束后, 截面背板上部分的应变进一步的减小, 这与理论分析过程中应变状态的分析是一致的。在型材上夹钳的受力端, 由于此处受到夹钳的载荷过于集中, 造成了该位置的应变的剧烈变化, 从图5中可以看出等效塑性应变的最大位置出现在该处, 因此实际生产过程中一般将该段型材废弃不用。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 成形过程中的等效塑性应变场Fig.5 Equivalent plastic strain distribution in forming process

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 拉弯零件回弹前、后对比Fig.6 Comparison between before and after springback

图6为型材回弹前、后的对比。通过使用Abaqus中的预定义场功能, 根据成形后的应力应变状态文件建立新的回弹分析模型, 模型中将成形过程中设置的边界条件和载荷均删除, 只观察成形后的应力应变场状态导致的回弹现象。可以看出优化后的模具型面可以大幅度减小回弹。

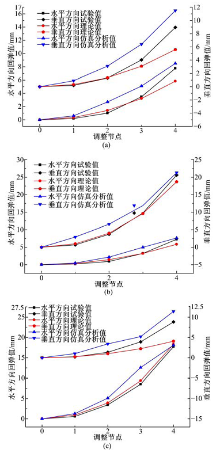
图7为T型材三维拉弯情况下的回弹结果对比, 其中, 黑色代表试验数据; 红色代表理论分析值; 蓝色代表了有限元仿真结果。通过两边不同的 Y轴参考坐标区分水平方向和垂直方向的回弹数据, 其中, 左侧为水平方向参数坐标, 右侧为垂直方向的参考坐标。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 三维拉弯结果比较Fig.7 Comparison of 3D stretch bending results

图7(a)中, r_hd=3.82 m, r_vd=3.82 m; 图7(b)中, r_hd=3.82 m, r_vd=1.91 m; 图7(c)中, r_hd=1.91 m, r_vd=3.82 m。

由图7可知, 理论模型计算结果与实际试验结果较为接近。当垂直方向上的弯曲变形较小时, 理论预测的回弹误差较大且小于实际测量值, 随着垂直方向上弯曲变形的增大, 回弹的理论预测值与实际测量值的差距逐步缩小。造成这种现象的原因如下所示。

(1)根据Capstan摩擦力模型, 已知摩擦力的大小与弯曲变形的大小有关。当弯曲变形较大时, 摩擦力的大小也随之增大, 拉弯成形实际的摩擦力减小了拉力对型材的拉伸作用, 而理论模型的计算过程忽略了摩擦力的作用, 因此导致了实际拉弯过程的应力值小于理论计算的应力值, 即回弹实际测量值大于理论模型预测值。

(2)由于轴向拉力的作用, 试验中, T型材的截面面积发生了变化, 且随着弯曲变形的加大, 截面面积相应缩小, 导致截面上的应力大于理论计算的应力值, 这一现象会抵消摩擦力对应力状态变化的影响。因此, 在上述两方面因素的共同作用下, 当补拉力作用在弯曲成形之后, 摩擦力影响将进一步被抵消, 使得回弹理论预测值逐步趋近于实际测量值。