作者简介:徐虹(1972-),女,副教授,博士.研究方向:轻量化材料组织和性能及成形控制.E-mail:xh@jlu.edu.cn
采用连续循环加载-卸载拉伸试验法研究了DP780的非弹性回复行为,确定了DP780在循环加载-卸载中应变回复的组成和比例。建立了卸载模量与塑性应变的数学模型。结合数值模拟和试验进行了模型验证。结果表明:DP780钢的平面各向异性不明显;由于卸载和重新加载循环非线性,卸载和重新加载轨迹构成了封闭环;卸载模量随着预应变的增大先快速下降,随后缓慢下降,在预应变达到6%后逐渐趋于稳定,卸载弹性模量降低17%;卸载总应变回复包括弹性部分和非弹性部分,并且后者所占比例高达11%。采用扫描电镜(SEM)和透射电镜(TEM)揭示了DP780非弹性回复的微观机理:塑性变形和奥氏体相变导致的位错密度增加,马氏体阻碍位错移动,造成大量的位错塞积,使可动位错发生弯曲,位错线长度增加,附加了弹性变形,导致了显著的非弹性回复行为。将得到的模型代入有限元模拟中,提高了模拟回弹的精度,使模具的回弹补偿更准确。
The inelastic recovery behavior of DP780 steel was studied in continuous cyclic loading-unloading tensile tests. The composition of springback and the percentage of inelastic strain recovery of the steel were determined. Then, a mathematical model of unloading modulus and plastic strain was proposed. The model was verified by numerical simulation and experiment. It is shown that the plane anisotropy of DP780 steel is not obvious. The unloading and loading paths constitute a closed loop, which is formed due to the nonlinearity of the elastic modulus in the unloading and reloading cycles. With the increase of the pre-strain, the elastic modulus decreases rapidly, which then increases slowly and gradually tends to be stable after the pre-strain reaches 6%, the unloading elastic modulus decreases by 17%. The total unloading strain recovery is composed of elastic strain recovery and inelastic strain recovery, and the inelastic strain recovery can reach as high as 11% of the total strain recovery. The microstructures of DP780 steel were detected by SEM and TEM, and the microscopic mechanism of the inelastic recovery was revealed. It is shown that the plastic deformation and austenitic phase transformation cause the increase of dislocation density; the martensite dislocation moving obstacles lead to a large amount of dislocation pile-up and the movable dislocation bending, increasing the length of the dislocation line and additional elastic deformation. This results in significant inelastic recovery behavior. Integrating the model to the finite element simulation improves the accuracy of simulated springback and the mold springback compensation is more accurate.
以DP钢为代表的先进高强度钢比强度高、延伸率大、碰撞性能好, 在汽车车身结构中的应用既可降低整车重量, 又可增加车身强度, 提高乘车安全性[1], 是汽车轻量化的理想材料。然而, 先进高强度钢因其强度高, 板料在成形过程中较普通钢具有更高的流变应力, 在模具圆角及拉延筋处因弯曲与反弯曲变形使其厚度方向应力分布不均而导致的包申格效应更加明显, 致使先进高强钢卸载后回弹更大且更加难以预测[2]。回弹预测的精度决定模具型面设计准确性及成形件的几何精度, 故精确地预测回弹对实现DP钢等先进高强度钢零部件的高精度成形及扩展先进高强钢的工程应用意义重大。
传统上将板料成形后卸载时的应变回复简化为弹性回复, 认为卸载时的弹性模量为恒定值, 但研究表明[3, 4, 5, 6]多种金属均存在弹性模量随塑性变形发生变化的现象, 即卸载过程中应力随应变的回复呈非线性变化, 这种现象被称为非弹性回复行为。对于DP钢而言, 其独特的微观结构使其在回弹预测中必须考虑弹性模量的变化。
DP钢等先进高强钢的非弹性回复现象已引起了国内外学者的广泛关注。Kim等[7]研究了Mild270、BH340、DP490和DP590四种不同强度级别钢卸载时的应变回复行为, 发现四种钢的卸载弹性模量均随预应变的增大而减小, 直至某一恒定值。Sun和Wagoner[8]以DP590、DP780和DP980为对象, 研究了双相钢在非线性加载路径下的流变行为, 构建了适用于DP钢塑性变形时的本构模型。Cleveland和Ghosh[9]对6022-T4铝合金和GP50XK60高强钢卸载时的应变回复行为进行了研究, 指出非弹性回复是成形卸载应变回复的主要构成之一, 其大小取决于成形时的应力状态。Abdel-Karim[10]研究了弹性模量对塑性变形数值模拟精度的影响, 指出基于变弹性模量的随动硬化模型具有更高的精度。Morestin和Boivin[11]指出加工硬化会导致钢弹性性能的改变, 如塑性应变达到5%时弹性模量会减小10%以上, 弹性模量的变化对回弹预测有明显影响。余海燕等[12, 13]分析了冷轧TRIP600钢板塑性变形过程中非弹性回复的规律及其产生的机理, 给出了弹性模量的拟合公式, 指出考虑弹性模量的变化能显著提高回弹仿真精度。庄京彪等[14]研究了DC06和DP600两种材料的包申格效应, 并比较了不同强化模型对回弹预测精度的影响, 指出随动强化和混合强化模型对高强钢冲压成形的回弹预测结果明显好于等向强化模型。房威[15]研究了强度水平和加载方式对包申格效应的影响, 指出强度水平高者, 其包申格效应就大, 反之包申格效应就小。Wagoner等[16]总结了近十年来关于回弹研究的进展, 将变弹性模量的研究单列为五大研究方向之一, 充分体现了变弹性模量在回弹研究领域中的重要地位。
为严谨起见, 本文把循环加载-卸载过程中的弹性模量称为卸载模量。综合上述研究可知:非弹性回复行为是卸载过程中应变回复的普遍现象, 且卸载模量是决定材料回弹性能的一个重要参数。目前鲜有DP780钢卸载过程中卸载模量与应变的量化关系及微观机理的研究, 为补充该方面的研究内容, 方便DP780先进高强钢的工程应用, 本文以DP780钢为研究对象, 利用循环加载-卸载拉伸试验法, 研究钢的非弹性回复行为, 对塑性变形前后的形貌和组成进行表征, 探讨非弹性回复行为的微观机理。将得到的卸载模量计算模型代入数值模拟软件中, 通过回弹数值模拟与试验结果的匹配程度来验证本文卸载模量计算模型的准确性。
试验材料采用某钢厂生产的双相钢DP780, 厚度为0.9 mm, 主要化学成分如下:w(C)≤ 0.18%, w(Si)≤ 0.8%, w(Mn)≤ 2.2%, w(P)≤ 0.05%, w(S)=0.015%, w(Al)=0.015%~1.5%, w(Cr)+w(Mo)≤ 1。
单向拉伸试验在MTS810电液伺服万能材料试验机上进行, 拉伸试样遵从国家标准GB/T228.1-2010, 试样尺寸如图1所示。为了研究材料各向异性对循环加载-卸载拉伸试验的影响, 拉伸试样沿着轧制方向、与轧制成45° 夹角及与轧制垂直方向通过线切割的方式进行切割, 各向异性拉伸试验的拉伸速度为2 mm/min。为了减小线切割对试样应力集中的影响, 对试样表面进行打磨, 磨后试样如图2所示。
循环加载-卸载拉伸试验的设备和试样尺寸与单向拉伸试验相同, 选择与轧制方向平行的拉伸试样。试验加载方法如图3所示。试验选定进行卸载的5个预应变分别是2%、4%、6%、8%和10%, 卸载通过与MTS810试验系统相连的计算机控制系统编程来实现, 首先将试样加载到应变2%下卸载,
然后再对同一个试样加载到应变4%下卸载, 如此反复直到加载10%后再卸载。每个应变水平下的卸载模量按下面的方法获取:首先对所测应力应变数据进行比较, 求得每次卸载时的准确真实应力应变水平值; 然后取得试验测得的应力应变曲线的弹性部分, 对这些数据进行多项式拟合; 最后对拟合所得多项式求导并求得零点处的导数值, 该值即为相应应变下的卸载模量值。
为了进一步揭示非弹性回复行为的微观机理, 对DP780钢的微观组织进行了扫描电镜观察, 试样腐蚀使用4%的硝酸酒精溶液, 腐蚀时间为7~10 s。采用JEM-2100F透射电镜对DP780钢未变形前、第2次卸载后和第5次卸载后的组织和位错组态进行了观察。
采用D/MAX-Ultima IV型X射线衍射仪对DP780钢中的组织进行了定性和定量分析。试验参数为:铜靶; 电压为40 kV; 电流为30 mA; 采用步进式扫描; 步宽为0.02° ; 速度为2° /min; 角度为40° ~105° 。
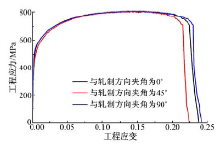
单向拉伸试验得到DP780钢在3个方向上的工程应力-应变曲线如图4所示, 可以看到DP780钢断裂前的应力-应变曲线基本重合, 平面各向异性不明显。
2.2.1 卸载行为的非线性
由于DP780钢的平面各向异性不明显, 所以选择与轧制方向平行, 应变速率为10-2 s-1的DP780钢板研究卸载模量的变化(取标距内中间位置)。
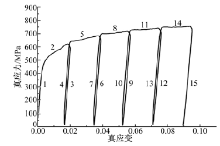
图5为DP780钢板在不同应变水平下卸载后的真实应力-应变曲线, 该曲线是由弹性直线1、初始加载曲线2, 五条卸载应力-应变线3、6、9、12、15, 四条硬化线5、8、11、14及加载应力-应变线4、7、10、13构成, 当开始加载时, 材料经历基于初始弹性模量的弹性变形, 然后遵从幂次硬化法则发生屈服和均匀塑性变形。仔细观察所有加载和卸载线均非直线, 且构成封闭环, 并且在每次卸载后又重新加载的真应力应变曲线并不是在卸载初始点处继续, 而是出现一个向上的小台阶, 这表明经过卸载-重新加载后, DP780钢的加工硬化能力有所提高, 硬化水平随变形增加而变化, 在均匀变形阶段, 应变硬化比较明显, 之后逐渐变小。
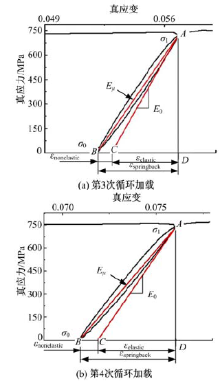
图6分别为DP780钢板第3次和第4次卸载-重新加载的典型循环, 其中:E0 是初始弹性模量; σ 1 是卸载瞬间的应力; σ 0是卸载结束点的应力。图6(a)中曲线AB为试验获得的卸载应力应变数据; 直线AB为连接卸载起始点A和卸载终止点B所得; 直线AC是依据弹性初始阶段计算得到的应力-应变直线。由图6可见, 当材料从应力A处开始卸载, 可以清晰地看出:卸载曲线的应力-应变关系为非线性关系, 实际卸载曲线AB在横轴的投影BD远大于直线AC在横轴的投影CD, 这表明卸载过程实际回复变形大于线性回复变形。因此, 卸载过程的总应变回复可以分为两部分:一部分为由初始弹性模量计算的弹性回复应变, 如图6(a)中CD部分所示, 另一部分为非弹性回复应变, 如图中的BC部分所示。图6(a)中总应变回复为0.0047, 其中非弹性回复应变所占比例约为11%, 而图6(b)中总应变回复为0.0052, 其中非弹性应变回复所占比例约为19%。由此可见, 随着塑性变形程度的增加, 非弹性应变回复所占比例逐渐加大。
2.2.2 非弹性回复卸载行为的数学模型
金属板料的非弹性回复行为的宏观表征可用卸载模量的变化来描述, 根据图5的应力-应变曲线以及试验方案中所述的计算方法可求得每个应变水平下卸载曲线所对应的卸载模量值, 如表1所示。
| 表1 卸载模量随塑性应变的变化 Table 1 Variation of unloading modulus with plastic strain |
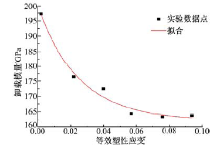
通过Origin软件将表1中数据绘成点图, 如图7所示。由图7可见:卸载模量随着应变的增加而逐渐减小, 卸载模量随着加载-卸载次数增加而下降, 第3次循环后(在预应变为6%左右)不再减小, 到试验结束时, 与初始弹性模量相比, 卸载模量降低了约17%后趋于饱和不再下降。将各等效塑性应变与卸载模量的数据对拟合为如下的数学模型, 该曲线呈现指数衰减规律。
式中:
图8是DP780钢未变形和第5次卸载后的扫描组织形貌。图8(a)是未变形的DP780钢的显微组织, 灰黑色块状为铁素体, 表面粗糙且有浮凸感呈灰白色的为马氏体, 带白色边圈、心部呈灰色的M-A岛和白亮的马氏体颗粒均匀地散布在纯净的铁素体基体上。M-A岛的形成是由于Mn通过铁素体或沿铁素体晶界扩散时, 在奥氏体岛的周围形成了高Mn的边圈, 使得奥氏体岛的边部比中心有更高的淬透性, 从而在冷却过程中形成了高锰的马氏体边圈及中心部分形成的渗碳体加铁素体的聚合体[17]。图8(b)为第5次卸载后的扫描组织形貌。
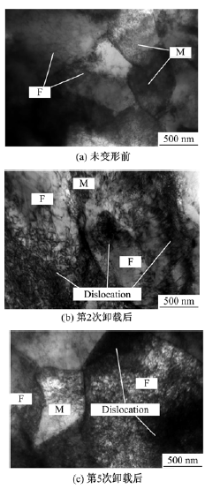
为了进一步探究非弹性回复行为, 对未变形、第2次卸载后和第5次卸载后的DP780钢进行了透射电镜分析。
DP780钢在未变形前的TEM照片如图9(a)所示, 中间发白的晶粒为马氏体(M), 铁素体(F)晶粒围绕在马氏体晶粒周围, 两者晶界较明显, 铁素体和马氏体晶粒中初始位错密度较低。图9(b)为经历第2次(加载到4%后卸载)卸载后TEM照片, 图中铁素体中的位错缠结程度和位错密度相对增多, 而马氏体中的位错缠结程度和位错密度相对减少。铁素体/马氏体小岛边界是塑性变形位错塞积的主要位置; 随着变形的继续增大, 当经历了第5次(加载到10%后卸载)卸载后两相的位错密度和位错缠结程度明显增大, 铁素体中的位错密度和位错缠结程度明显大于马氏体位错密度和位错缠结程度, 如图9(c)所示。
金属材料的塑性变形过程与位错运动密切相关, 双相钢在塑性变形过程中, 塑性应变主要分布在铁素体基体中。当铁素体发生较高的塑性变形时, 铁素体/马氏体界面形成严重的应力集中, 马氏体开始参与塑性变形。但由于马氏体中位错运动困难, 马氏体中的塑性变形是十分有限的。双相钢的塑性很大程度上取决于铁素体/马氏体界面对塑性变形的协调能力。
从宏观角度来看, 弹性模量是用来衡量材料抵抗弹性变形能力大小的尺度; 从微观层面讲, 弹性模量是用来表征原子、离子、分子之间相互结合力(键合强度)的大小。因此, 凡是影响键合强度的因素均能影响材料的弹性模量。弹性模量随塑性变形的变化规律与空位及位错等晶体缺陷有直接关系, 点阵的畸变程度也对弹性模量有很大影响。
在DP780钢中, 由于马氏体岛硬度很高, 这就相当于形成了微观层面上的位错钉扎点, 这些所谓新增钉扎点就会改变原子局部区域的应力场导致点阵畸变加剧, 在发生塑性变形的过程中会形成很多空位和位错等缺陷, 很多原子、离子或分子借助于这些缺陷发生了转移, 偏离了原始平衡位置, 此时使原子势能增大, 原子活动能力加强, 所以用来表示原子间键合强度的弹性模量值会出现减小的趋势。
DP780钢在变形初期, 由于晶体内位错增殖, 可动位错密度大大增加, 所以在塑性变形较小时的弹性模量下降速度很快。当塑性变形量继续增大, 虽然位错仍会增殖, 缺陷依然会产生, 但是位错等缺陷之间会发生强烈的交互作用进而形成位错缠结、位错胞和高密度的位错墙, 这些位错缠结以及高密度位错墙会阻碍位错的进一步运动, 导致可动位错的数量趋于饱和, 因此, 随着塑性变形量的增大, 弹性模量值减小的速度放缓并且逐渐趋于饱和。由于位错密度的增加以及位错的塞积, 位错线在变形前是如图10(a)所示的直线, 其中Le为杂质钉间的距离, 位错塞积导致位错线发生弯曲, 位错线长度增加, 如图10(b)所示。
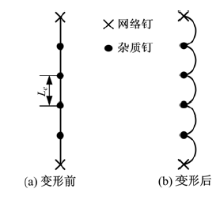 | 图10 塑性变形过程中可移动位错线弯曲示意图Fig.10 Schematic diagram of movable dislocation lines curved process during plastic deformation |
根据位错理论, 位错线长度的增加可产生附加弹性变形, 使卸载模量发生改变, 产生了显著的非弹性回复行为。
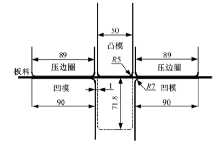
基于Numisheet 2011标准考题BM4, 将卸载模量模型输入Pamstamp-2G软件中, 对典型的U型截面件进行冲压成形回弹模拟。模拟模型的几何参数如图11所示, U型件回弹后轮廓及回弹量的测量方法如图12所示。板料尺寸为360 mm× 30 mm, 冲压深度为71.8 mm。材料模型采用Yoshida随动硬化模型。成形过程中, 压边力为10 kN, 摩擦因数为0.12。
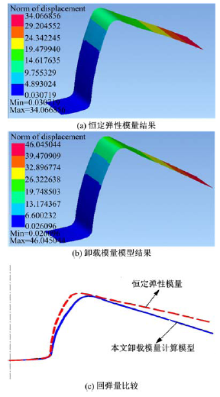
图13为恒定弹性模量和卸载模量模型的模拟结果。由图13可知, 考虑卸载模量随应变发生变化情况下得到的回弹量比恒定弹性模量情况下的回弹量大。这是由于板料发生变形后, 卸载性模量减小, 从而导致回弹量增大。回弹模拟结果如表2所示。由表2可知, 卸载模量的模拟结果与试验结果更吻合, 说明考虑变形过程中卸载模量的变化可显著提高回弹模拟的精度。
| 表2 模拟与试验回弹量测量结果 Table 2 Springback values of simulation and test |
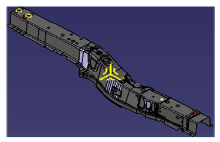
汽车梁柱件的截面基本都是U型, 但沿长度方向形状变化较大, 简单U型件不能反映汽车梁柱件实际冲压成形回弹情况, 为此选择形状较为复杂的边梁进行试验, 其结构如图14所示, 在AutoForm软件中建立如图15所示的有限元模型, 将式(1)输入AutoForm成形模拟软件, 模拟边梁成形, 并根据回弹模拟结果设计能够精确回弹补偿的边梁冲压模具, 并进行冲压试验, 发现其回弹比恒定弹性模量回弹稍大, 根据模拟结果, 在边梁模具上进行回弹补偿, 得到合格边梁制件, 如图16所示, 验证式(1)的准确性。
(1)DP780钢平面各向异性行为不明显; 卸载弹性模量随着预应变增加而降低, 在预应变为6%左右趋于稳定, 卸载弹性模量降低了约17%后趋于饱和不再下降; 卸载过程的总应变可以分为弹性应变和非弹性回复应变两部分, 非弹性回复应变所占比例约为11%; 通过指数拟合, 建立了卸载弹性模量与预应变的数学模型, 用该模型模拟预测回弹比用恒定弹性模量预测回弹更接近试验值。
(2)DP780钢在变形过程中导致了大量的位错塞积, 马氏体硬质相对位错起了钉扎的作用, 增加了位错线长度和弯曲程度, 从而产生了显著的非弹性回复行为。
(3)在边梁模具上进行的实验表明:采用本文的卸载模量模型提高了回弹模拟的结果, 模具回弹补偿更加准确。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|