引用本文
赵宏伟, 王振, 杨文迪, 刘萍萍. 熵 选 择 多 重 二 进 制 编 码. 2017, 47(1): 218-226
ZHAO Hong-wei, WANG Zhen, YANG Wen-di, LIU Ping-ping. Multiple binary codes based on entropy selection. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 218-226  
Permissions
Copyright©2017, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
熵 选 择 多 重 二 进 制 编 码
赵宏伟1,2, 王振1, 杨文迪3, 刘萍萍1,2
1.吉林大学 计算机科学与技术学院,长春 130012
2.吉林大学 符号计算与知识工程教育部重点实验室,长春 130012
3.华东师范大学 计算机科学与软件工程学院,上海 200062
通讯作者:刘萍萍(1979-),女,副教授,博士.研究方向:计算机视觉.E-mail:liupp@jlu.edu.cn

作者简介:赵宏伟(1962-),男,教授,博士生导师.研究方向:计算机视觉.E-mail:zhaohw@jlu.edu.cn

基金:国家自然科学基金项目(61101155); 吉林省自然科学基金项目(20140101184JC,20150520063JH); 吉林大学研究生创新基金项目(2015051).
摘要

为了解决查询高维浮点型数据的近邻点需要计算代价昂贵的欧式距离,内存占用率较高的问题,将高维浮点型数据通过哈希映射函数映射为低维二进制编码,并保证同一样本点在两种空间内的归一化距离满足相似性。从而在实现近邻检索任务时,可使用代价较低的汉明距离替换欧式距离,达到降低检索复杂度的目的。为保证由哈希函数生成的二进制编码具有较优的近邻检索性能,本文首先基于查找机制得到数据集适应空间分布特性的二进制标签,然后利用SVM算法得到二进制标签的分类平面,并选择其中具有最大熵值的平面函数作为最终的哈希映射函数。为了进一步提高近邻检索性能,在训练阶段,初始化多种不同的编码中心点用以生成多重二进制标签,并得到与此相应的多重哈希函数和多重二进制编码。在检索过程中,建立了基于多重二进制编码的近邻检索体系,返回具有较小平均汉明距离的样本点作为最终检索结果。实验结果表明:与其他现存优秀算法相比,本文算法可以快速、有效地将浮点型数据转化为二进制编码,而且基于这些二进制编码的近邻检索性能较优。

关键词: 计算机应用; 近邻检索; 二进制特征; 哈希编码; 熵
中图分类号:TP391.41 文献标志码:A 文章编号:1671-5497(2017)01-0218-09
Multiple binary codes based on entropy selection
ZHAO Hong-wei1,2, WANG Zhen1, YANG Wen-di3, LIU Ping-ping1,2
1.College of Computer Science and Technology, Jilin University, Changchun 130012, China
2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education, Jilin University,Changchun 130012, China
3.School of Computer Science and Software Engineering, East China Normal University,Shanghai 200062,China
Abstract

Searching for Approximate Nearest Neighbors (ANN) of high dimensional floating point data has to compute their expensive Euclidean distances, and the memory occupancy rate is high. In order to fix such problem, an algorithm is proposed to effectively and efficiently map high dimensional floating point data into low dimensional binary codes, while preserving the normalized distance similarity. As a result, Hamming distances can be used to instead the Euclidean distances during ANN search process. To guarantee the ANN search performance of obtained binary codes, the distribution adaptive binary labels of the training data are firstly acquired based on the look-up mechanism. Then, the classifaction planes are obtained on the basis of SVM algorithm, and the one with the highest entropy value is chosen as the final hashing function. In order to further improve the retrieval performance, the retrieval system based on multiple binary codes is proposed. During the training process, different kinds of original encoding centers are chosen to obtain multiple hashing functions and multiple binary codes. During the search stage, the points with the minimal average Hamming distances are returned as query results. Experiments show that the proposed algorithm can efficiently and effectively map the floating point data into superior binary codes, and has excellent ANN search performance when compared with other state-of-art methods.

Keyword: computer application; approximate nearest neighbor search; binary codes; Hashing algorithm; entropy
0 引 言

图像检索任务可通过比较两幅图像的SIFT特征描述子[1]或GIST特征描述子[2]的相似性来实现, 然而这些特征描述子均以高维浮点数的形式存在, 直接检索这些特征描述子的近邻点, 需要计算昂贵的欧式距离。随着网络共享技术以及云存储技术的发展, 网络图像数量呈指数增长。庞大的数据将会导致计算量过大, 内存占用率过高等问题, 从而不能及时返回图像检索结果。为了解决这一问题, 人们开始关注如何将高维浮点型数据转换为低维二进制编码, 并在汉明空间内进行近邻检索[3], 从而只需调用计算机硬件指令执行异或操作便可得到特征点之间的汉明距离, 此计算过程复杂度低、速度快、内存占用率低。

哈希算法[4, 5, 6]可以将高维浮点型数据编码为低维的二进制编码, 并保证在原空间内相似的特征点对被映射至汉明空间后仍然具有相似性。最早提出哈希思想的是局部敏感哈希(Locality sensitive hashing, LSH)算法[7], 该算法是较经典的哈希算法, 然而LSH算法的哈希映射函数是随机生成的, 与数据无关, 导致其近邻检索性能并不能随着二进制编码位数的增加而显著提高。谱哈希(Spectral hashing, SH)算法[5]基于谱图分割得到高维浮点型数据的二进制编码, SH算法首先根据特征点之间的相似性建立权重图, 然后分割权重图并将同一类数据编码为相同的二进制编码, 但SH算法要求数据集在高维空间内服从均匀分布, 这一要求与实际情况大多不相符, 导致SH算法性能较差。ITQ(Iterative quantization)算法[8]通过旋转数据集将其映射至与其距离最近的超立方体顶点, 并根据顶点坐标的符号得到数据集的二进制编码。与SH算法相比, ITQ算法不再要求数据集服从比较特殊的均匀分布, 并且使用相似性误差作为约束条件, 保证了所生成的哈希函数具有较优的性能。量化误差, 一种类似于在k-means聚类算法[9]中的定义, 被KMH(K-means hashing)算法[10]引入, 与相似性误差共同作为生成哈希函数的约束条件。KMH算法通过迭代机制, 同时优化量化误差和相似性误差, 使得最终生成的二进制编码具有最优的表现性能。

KMH算法依据哈希算法的编码机制, 将现有的哈希算法大致分为3类:基于查找的哈希算法、基于映射的哈希算法和其他算法。基于查找的哈希算法[11], 如KMH算法, PQ(Product quantization)算法[12], OPQ(Optimized product quantization)算法[13], 这些算法首先建立编码中心点(拥有二进制编码的高维浮点型数据)集, 然后比较新样本点与每一个编码中心点之间的距离, 并赋予新样本点与其距离最近的编码中心点相同的二进制编码。基于映射的哈希算法, 如LSH算法[7]和ITQ算法[14], 这类算法的哈希函数为线性映射函数。基于映射的哈希算法根据新样本点与线性哈希映射函数的映射结果的符号, 将新样本点编码为二进制编码。基于查找的哈希算法所生成的二进制编码对数据集在欧式空间内的分布特性有较强的自适应性, 近邻检索性能较好。但基于查找的哈希算法的编码时间复杂度较高, 若将新样本点编码为m位二进制编码, 需要计算新样本点与2m个编码中心点之间的距离关系, 该编码过程的时间复杂度为O(2m)。同样将一个新样本点编码为m位二进制编码, 基于映射的哈希算法只需要计算新样本点与m个线性哈希函数的映射结果。如此, 基于映射的哈希算法的编码时间复杂度仅为O(m), 但是, 基于映射哈希函数所生成的二进制编码的近邻检索性能比基于查找的哈希算法的性能差。

为保证所得二进制编码具有较优的近邻检索性能, 哈希算法应满足相似性保持约束条件。良好的约束条件能够保证在原空间内相似的特征点对被映射至汉明空间后, 它们之间汉明距离不大于非相似的特征点对。这种约束条件保证了在近邻查询过程中, 可以使用特征点之间的汉明距离代替欧式距离。Wang等[15]详细探讨了各种各样的相似性约束条件。Gong等人[14]在学习哈希映射函数时, 引入了量化损失误差。序列保持哈希算法要求所生成的二进制编码应满足排列一致性准则[15], 语义哈希算法旨在保持数据点之间的语义相似性[16], Norouzi等人[17, 18]要求保持三元组之间的相对关系, Wang等人[19]定义了铰链损失函数。为保证由本文所生成的哈希函数得到的二进制编码之间的汉明距离可以近似代替其欧式距离, 本文提出了归一化距离相似性约束条件。该条件要求两个样本点之间的归一化汉明距离与其相对应的归一化欧式距离相近。从而可以使用汉明距离代替欧式距离, 这将降低近邻检索的复杂度。

本文算法的哈希映射函数经过两步机制[20, 21, 22]生成。第1步, 利用基于查找的机制[10]优化归一化距离相似性保持约束条件和量化误差约束条件, 得到二进制标签。第2步, 利用二制标签作为监督信息, 通过SVM算法得到分类平面[20], 并选择拥有最大熵值的平面函数作为最终的哈希函数。根据新样本点与线性哈希函数的映射结果的符号, 将其编码为二进制编码, 该编码机制属于基于映射的哈希算法[7], 编码时间复杂度较低, 而且哈希函数是在基于查找机制得到的二进制标签的监督下生成的, 保证了其良好的近邻检索性能。借助于两步机制, 本文在不显著降低所得二进制编码性能的前提条件下, 提高了编码效率。

为了避免由于二进制标签的种类数量与实际数据集类别的数量不相同而影响近邻检索性能, 本文提出初始化不同的编码中心点生成多重哈希函数以及相应的多重二进制编码。在检索过程中, 建立了基于多重二进制编码的检索体系, 将平均汉明距离最小的点作为最终的检索结果, 从而提高近邻检索性能。

1 约束条件
1.1 归一化距离相似性保持约束

在近邻检索任务中, 为保证基于特征点的二进制编码所计算出来的汉明距离可以近似代替其欧式距离, 其二进制编码应满足相似性保持约束条件[5]。基于这一基本原则, 本文定义了归一化距离相似性保持约束条件。该约束条件能够保证汉明距离可以近似代替相对应的欧式距离, 从而使得在两个空间内得到的检索结果相近。

归一化距离相似性保持约束条件描述如下:

给定一个样本点xi∈ X, 那么xi 与数据集中其他的点之间的汉明距离所构成的汉明距离集合表示为:nH={nh1, nh2, …, nhn}, 对其进行归一化处理后, 得到归一化汉明距离为:nH'={nh'1, nh'2, …, nh'n}。相应地, 在欧式空间可以得到它们的欧式距离集合:nD={nd1, nd2, …, ndn}以及归一化欧式距离集合:nD'={nd'1, nd'2, …, nd'n}。优秀的二进制编码可以使得式(1)的值最小, 从而在检索过程中, 可以保证其汉明距离能够近似代替相应的欧式距离。

S(xi)=∑j=1n1-nh'ijnd'ij(1)

式中:nh'ij 表示数据点xi和xj之间的归一化汉明距离; nd'ij表示数据点xi和xj之间的归一化欧式距离。

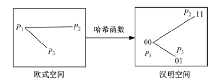
数据点xi和其他点之间的归一化欧式距离是固定的, 因此优秀的二进制编码应该使得nh'ij能够近似代替nd'ij 。如图1所示, 欧式空间内的点被映射至汉明空间, 并被要求满足归一化距离相似性约束条件时, 可以保证样本点对之间的相对汉明距离关系与其欧式相对距离关系相一致。

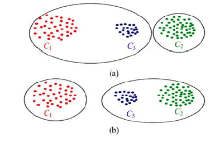
图1 满足归一化距离相似性保持约束条件的二进制编码Fig.1 Normalized distance similarity preserving binary codes

1.2 量化误差

若将数据集中的所有样本点编码为m位二进制编码, 则依据样本点的二进制编码对其进行分类, 所有数据点可以被分成2m 种。然而数据集的样本容量n要远远大于2m, 因此许多样本点将被编码为相同的二进制编码。为了使二进制编码符合空间分布特性, 本文要求被编码为相同二进制编码的样本点在原始空间内互为近邻关系。将样本点编码为二进制编码时, 若不要求具有相同二进制编码的样本点在空间内互为近邻关系, 则可能出现如图2(a)中所示的编码情况, C3与C1被分为同一类并被编码为相同的二进制编码。按照这种编码原则, 计算得到C3 与C1 之间的汉明距离为0, 而C1 与C2 之间的汉明距离为1。但根据欧式空间内3类数据的分布情况, 可知C3 与C2 互为近邻关系, 因此应将C3 与C2编码为相同的二进制编码。为避免图2(a)中的情况, 得到如图2(b)中所示满足欧式空间分布特性的二进制编码, 本文要求所得样本点的二进制编码应当最小化量化误差的值。量化误差定义如下:

qua(x)=∑i=1n[xi-C(xi)](2)

式中:xi表示样本点; C(xi)表示样本点xi的编码中心(xi的聚类中心且拥有二进制标签)。最小化式(2)可以保证具有相同二进制编码的样本点在空间内互为近邻关系。

图2 量化误差约束条件Fig.2 Restriction of quantization error

本文将归一化距离相似性误差和量化误差共同作为约束条件, 从而既能保证样本点对之间的汉明距离关系可近似代替其欧式距离关系, 又能保证具有相同二进制编码的样本点在欧式空间内互为近邻关系。

2 哈希映射函数
2.1 二进制标签

本文所提算法的目标函数 E是归一化距离相似性误差与量化误差之和, 即:

E=∑i=1nS(xi)+qua(xi)(3)

通过最小化 E的值可得到每一个样本点的最优二进制标签。本文采用迭代梯度下降法[9]优化目标函数 E, 当迭代过程收敛时, 便可得到数据集的聚类中心及其相应的二进制编码。

为了使目标函数能够以最快的速度收敛, 本文采用类似于PQ(Product quantization)算法[12, 13]的机制, 将原数据的维度分配到多个子空间, 并在每个子空间内分别采用迭代梯度下降算法得到子二进制编码, 最后组合这些子二进制编码得到最终的二进制编码。例如将128维的SIFT特征[1]编码为64位二进制编码, 可以通过类似PQ的机制, 将SIFT特征的128个维度平均分配到16个子空间内, 每个子空间含有原SIFT数据集的8个维度, 在每个子空间内只需将这些8维数据编码为4位二进制编码, 最后组合这16个子空间内的4位二进制编码便可得到最终的64位二进制编码。

在每个子空间内, 本文所执行的迭代优化算法包括以下3个基本步骤:

(1)若将样本点编码为b位二进制编码, 则从训练数据集中随机选取2b 个样本点作为初始编码中心点, 并赋予它们互不相同的b位二进制编码。

(2)计算训练数据集中所有数据点与每个编码中心点的距离关系, 并将其分配给与其距离最近的编码中心点, 同时将其编码为与其距离最近的编码中心点相同的二进制编码。

(3)更新编码中心点。依次更新每一个编码中心点, 并将除当前正在更新的编码中心点以外的点看作常量。采用梯度下降法[9]优化目标函数 E, 得到一个匹配当前二进制编码的最优样本点作为编码中心点。

在每个子空间内, 不断重复步骤(2)和(3)直至收敛, 将得到所有二进制编码的最优编码中心点。样本集中其余的点将被编码为与其距离最近的编码中心点相同的二进制编码, 这样就得到了所有样本点的二进制标签。

2.2 监督学习哈希映射函数

2.1节通过迭代梯度下降机制优化目标函数 E, 得到最优编码中心点。通过比较新样本点与编码中心点的距离关系, 可将新样本点编码为与其距离最近的编码中心点相同的二进制编码[10]。然而这种编码方法的时间复杂度过高, 若将样本点编码为m位二进制编码, 则需计算新样本点与2m 个编码中心点的距离关系, 时间复杂度为O(2m)。但基于映射的哈希算法[7, 14] 只需计算新样本点与m个哈希映射函数的映射符号, 时间复杂度仅为O(m), 编码效率较高。为了提高本文得到二进制编码的效率, 本节将利用2.1节得到的二进制标签作为监督信息, 学习得到哈希映射函数。

哈希映射函数将样本点映射为具有符号的实数, 并根据映射结果的符号将样本点编码为不同的二进制编码, 编码规则如式(4)所示:

bj(xi)=1, fj(xi)> 00, otherwise(4)

式中:bj(xi)表示样本点xi 的第j位二进制编码; fj(• )表示对应第j位二进制编码的哈希函数。

由式(4)可知, 第j位哈希函数只决定样本点的第j位二进制编码的值; 反之, 对应第j位二进制编码的哈希函数由所有样本点的第j位二进制编码的分布情况决定。根据样本点的二进制编码中的第j位编码不同而其余位均相同的原则, 可将样本点分成2m-1组。在每组内利用SVM分类算法可得到一个基于第j位二进制编码的分类平面, 这些平面为fj (• )的候选哈希映射函数。

例如, 在2.1节中, 每一子空间内的数据集被编码为 b=4位二进制标签, 若求对应右边第1位二进制编码的哈希映射函数, 首先依据数据集二进制编码的第1位不同其余位均相同的原则将数据集分为2b-1=8组:(0000, 0001); (0010, 0011); (0100, 0101); (0110, 0111); (1000, 1001); (1010, 1011); (1100, 1101); (1110, 1111)。然后依据每组数据均可得到一个哈希映射函数。

如上所述, 根据具有m位二进制标签的数据集可得到2m-1个分类平面作为计算每一位二进制编码值的哈希映射函数。然而最终的编码过程只需要一个哈希映射函数便可得到一位二进制编码的值。通过比较2m-1个哈希函数的熵值, 从中选择拥有最大熵值的函数作为最终的哈希映射函数,

并将其用于编码新样本点。哈希函数的熵值可由式(5)计算得到。

entropy(fj)=-P(1)log(P(1))-P(0)log(P(0))(5)

式中:entropy(fj)表示映射函数fj的熵值, P(• )表示样本集被编码为该值的概率。训练过程中, 正负样本的数量相等, 则当被编码为0和1的样本各为总训练样本集的一半时, 该哈希函数的熵值最大。熵值表示信息的不确定性, 熵值越大, 其函数的编码情况越符合上述情况, 性能越优。

3 基于多重二进制编码的查询机制

第2节中的线性映射函数与初始编码中心点的位置有关。不同的初始编码中心点可能会得到不同的二进制标签, 从而生成不同的线性映射函数。为了削弱这一影响, 本文多次随机选择不同的样本点作为初始编码中心点, 当目标函数收敛时, 数据集的二进制标签会有所差异, 并得到不同的哈希映射函数, 而且这些哈希映射函数分别为对应不同初始编码中心点的局部最优哈希函数。本文将这些对应于不同初始编码中心点的多个哈希函数称为多重哈希函数。

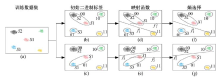
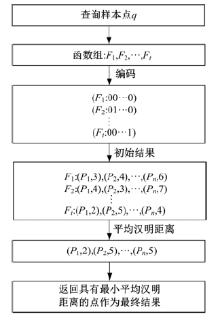
多重哈希函数训练过程如图3所示。当所选择的初始编码中心点不同时, 最小化目标函数 E, 得到的二进制标签会有所不同。图3中S1样本点和S2样本点的相对空间分布与S1样本点和S3样本点的相对空间分布相一致。若初始样本点从S1样本点和S3样本点中选择, 当目标函数收敛时, 会得到如图3(b)所示的二进制标签。若从S1样本点和S2样本点中选择初始编码中心点, 当目标函数收敛时, 得到的二进制标签如图3(c)所示。如2.2节所述, 依据数据集的每一种两位二进制标签, 均可得到两个用于计算数据集每一位二进制编码值的哈希映射函数。对应于右边第一位二进制编码值的哈希映射函数组分别为 (f11, f12)和(f21, f22), 如图3(d)(e)所示。通过计算并比较每组内两个哈希函数的熵值, 函数 f11和f21被选择作为每组的最终哈希函数。S1样本点被哈希函数 f11和f21编码为不同的二进制编码, 而其余样本点基于这两个哈希函数得到的二进制编码是一致的, 如图3(f)(g)所示。

图3 多重哈希函数训练框架Fig.3 Training framework of multiple hashing functions

基于多重哈希函数与相应的多重二进制编码的近邻检索的流程如图4所示。首先查询点 q被训练阶段得到的多重哈希函数组映射成不同的二进制编码, 然后计算 q与数据库中的点基于相同组的哈希函数的汉明距离, 最后计算其平均汉明距离, 如式(6)所示:

(6)

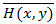表示样本点x和y之间的平均汉明距离; Hi(x, y)表示样本点x和y基于第i组哈希函数Fi的汉明距离, 共有t组哈希函数。最后, 返回与查询点之间的平均汉明距离最小的点作为最终结果。

图4 近邻查询过程Fig.4 Flowchart of ANN search

基于多重二进制编码的查询机制可以提高近邻查询性能。如图3所示, 在欧式空间内, S1样本点与S2样本点和S3样本点的相对距离相同。当查询S1样本点的近邻时, 若只采用一组哈希函数, 那么所返回的近邻点只包括S2样本点或S3样本点。然而采用多重二进制编码, 可将S2样本点和S3样本点均当作S1样本点的近邻点返回, 从而提高了近邻查询的性能。

4 实验结果
4.1 数据集及评价标准

SIFT和GIST是图像检索中较为常用的两种特征描述子, 这两种特征的近邻检索性能直接影响图像的检索效果。本文分别利用Labelme图像库[23]的SIFT特征和Cifar10图像库[24]的GIST特征比较本文所提算法和其他算法的性能。利用VL_SIFT算法[25]提取Labelme数据库图像的128维浮点型SIFT特征描述子, 并采样组成含有1000 000个训练数据集和10 000个测试集的Labelme_SIFT数据库。提取Cifar10图像的320维浮点型GIST特征描述子, 并组成含有50 000个训练样本点和10 000个测试样本点的Cifar10_GIST数据库。

本文采用召回率(recall), mAP[26]和精确度(precision)三种标准评价各个算法的性能。

召回率(recall)表示检索到的正样本数量占所有正样本数量的比例, 计算公式如下:

recall=#(retrievedpositive)#(allpositive)(7)

#(retrieved positive)表示检索到的正样本数量, #(all positive)表示训练数据集中所有正样本的数量。

mAP值定义如下:

mAP=1Q∑i=1Q∑j=1Ki[j/rank(j)]/Ki(8)

式中:mAP值衡量正样本的返回速率; |Q|表示查询样本点的数量; Ki表示与第i个查询样本点相关的正样本数量; rank(j)返回第j个正样本在最终查询结果中的排列序号。

精确度(precision)表示检索到的正样本数量占所有已返回样本数量的比例, 其值可由式(9)计算得到, #(retrieved points)表示查询到的样本数量。

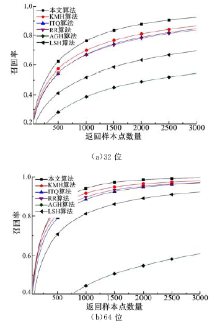
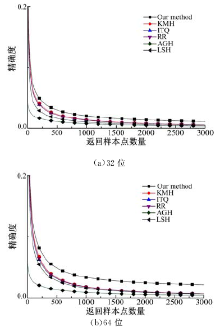
precision=#(retrievedpositive)#(retrievedpoints)(9)

4.2 实验结果

Labelme_SIFT数据库含有1000 000个SIFT特征描述子, 从中随机选取100 000个样本点作为训练数据集, 训练得到多重哈希映射函数。根据多重哈希函数, 将数据库中100 000个样本点和10 000个测试集编码为多重二进制编码, 然后计算每个测试样本点与所有训练样本点之间的平均汉明距离, 并返回具有较小平均汉明距离的样本点作为检索结果。统计得到每种算法的recall曲线和precision曲线如图5和图6所示, mAP值如表1所示。

图5 各个算法在Labelme_SIFT数据集上的召回率曲线Fig.5 Recall curves in Labelme_SIFT data base

图6 各个算法在Labelme_SIFT数据集上的精确度曲线Fig.6 Precision curves in Labelme_SIFT data base

表1 各个算法在Labelme_SIFT数据集上的mAP值 Table 1 mAP values of algorithms in Labelme_SIFT %

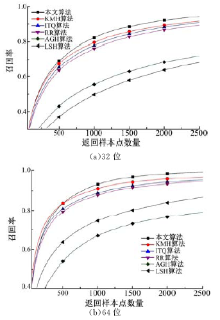
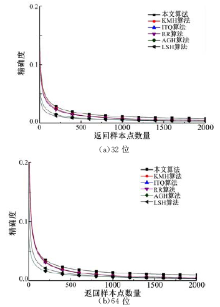
基于Cifar10_GIST数据库中的50 000GIST描述子训练, 训练得到多重哈希映射函数。并将训练数据集和测试数据集编码为多重二进制编码, 计算测试样本点与训练样本点之间的平均汉明距离并返回具有较小值的样本点作为最终的返回结果。算法表现结果如图7、图8和表2所示。

图7 各个算法在Cifar10_GIST数据集上的召回率曲线Fig.7 Recall curves in Cifar10_GIST data base

图8 各个算法在Cifar10_GIST数据集上的精确度曲线Fig.8 Precision curves in Cifar10_GIST data base

表2 各个算法在Cifar10_GIST数据集上的mAP值 Table 2 mAP values of algorithms in Cifar10_GIST %

从以上实验结果可知, 本文算法得到的二进制编码的近邻检索性能优于KMH算法[10]、ITQ算法[14]、RR算法[11]、AGH算法[27]和LSH算法[7]。本文算法与KMH算法相比, 采用了归一化距离相似性约束条件, 并且提出了基于多重哈希函数的查找机制, 从而保证了二进制编码的近邻检索性能。ITQ算法和RR算法的基本原理相似, 均通过旋转数据将其映射至超立方体的顶点, 然后根据顶点坐标的符号将其编码为二进制编码。但ITQ和RR算法只考虑了相似性误差, 忽略了量化误差, 使得数据集的二进制编码不能很好地适应数据的空间分布特性。本文算法除了将归一化距离相似性误差作为限制约束条件外, 还将量化误差作为计算二进制编码的约束条件, 保证所得二进制编码能够很好地适应数据集的空间分布特性。LSH算法的哈希映射函数是随机产生的, 与数据无关, 其性能不能随着二进制编码位数的增加而迅速提高。本文算法不但具有优秀的近邻检索性能, 而且编码效率也较高。比较各个算法将100 000个SIFT特征描述子编码成二进制编码所需的时间如表3所示。从表中可以看出, 本文算法和LSH算法的编码速度要比其他算法快。

表3 各个算法编码一百万数据点所需的时间 Table 3 Time consumed for encoding one million data points s
5 结束语

本文算法能够快速有效地将高维浮点型数据映射为低维的二进制编码, 并且在近邻检索中, 能够使用汉明距离代替欧式距离, 从而降低近邻检索的复杂度。本文算法将归一化距离相似性误差和量化误差共同作为约束条件, 保证所得二进制编码具有较优的近邻检索性能。为加快编码速率, 本文以二进制编码作为监督信息得到线性哈希映射函数, 使本文算法的编码时间复杂度随着二进制编码长度的增加曾线性增长而非指数增长。本文选择具有最大熵值的哈希函数作为最终的哈希函数, 并建立了基于多重哈希函数的检索体系, 共同保证近邻检索性能。最终的实验结果表明, 本文算法的性能优于其他算法。

The authors have declared that no competing interests exist.

参考文献
[1] Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. [本文引用:2]
[2] Oliva A, Torralba A. Modeling the shape of the scene: a holistic representation of the spatial envelope[J]. International Journal of Computer Vision, 2001, 42(3): 145-175. [本文引用:1]
[3] Wang Jun, Kumar S, Chang S F. Semi-supervised hashing for scalable image retrieval[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), San Francisco, Ca, USA, 2010: 3424-3431. [本文引用:1]
[4] Weiss Y, Fergus R, Torralba A. Multidimensional Spectral Hashing[M]. Berlin Heidelberg, Springer, 2012: 340-353. [本文引用:1]
[5] Weiss Y, Torralba A, Fergus R. Spectral hashing[C]//Proceedings of the Advances in Neural Information Processing Systems, Vancouver, British Columbia, Canada, 2008: 1753-1760. [本文引用:3]
[6] Liu Wei, Wang Jun, Ji Rong-rong, et al. Supervised Hashing with kernels[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Rhode Island , 2012: 2074-2081. [本文引用:1]
[7] Indyk P, Motwani R. Approximate nearest neighbors: towards removing the curse of dimensionality[C]//Proceedings of the 30th Annual ACM Symposium on Theory of Computing, Dallas, Texas, 1998: 604-613. [本文引用:5]
[8] Gong Y C, Lazebnik S, Gordo A, et al. Iterative quantization: a procrustean approach to learning binary codes for large-scale image retrieval[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(12): 2916-2929. [本文引用:1]
[9] MacQueen J. Some methods for classification and analysis of multivariate observations[C]//Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, California, 1967: 281-297. [本文引用:3]
[10] He Kai-ming, Wen Fang, Sun Jian. K-means hashing: an affinity-preserving quantization method for learning binary compact codes[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland , Oregon, 2013: 2938-2945. [本文引用:4]
[11] Jegou H, Douze M, Schmid C, et al. Aggregating local descriptors into a compact image representation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), San Francisco, 2010: 3304-3311. [本文引用:2]
[12] Jegou H, Douze M, Schmid C. Product quantization for nearest neighbor search[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(1): 117-128. [本文引用:2]
[13] Ge Tie-zheng, He Kai-ming, Ke Qi-fa, et al. Optimized product quantization[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(4): 744-755. [本文引用:2]
[14] Gong Yun-chao, Lazebnik S. Iterative quantization: a procrustean approach to learning binary codes[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, 2011: 817-824. [本文引用:4]
[15] Wang Jian-feng, Wang Jing-dong, Yu Neng-hai, et al. Order preserving hashing for approximate nearest neighbor search[C]//Proceedings of the 21st ACM International Conference on Multimedia, Barcelona, Spain, 2013: 133-142. [本文引用:2]
[16] Salakhutdinov R, Hinton G. Semantic hashing[J]. International Journal of Approximate Reasoning, 2009, 50(7): 969-978. [本文引用:1]
[17] Norouzi M, Blei D M. Minimal loss hashing for compact binary codes[C]//Proceedings of the 28th International Conference on Machine Learning (ICML), Bellevue, Washington, 2011: 353-360. [本文引用:1]
[18] Norouzi M, Blei D M, Salakhutdinov R. Hamming distance metric learning[C]//Proceedings of the Advances in Neural Information Processing Systems, South Lake Tahoe, Nevada, 2012: 1061-1069. [本文引用:1]
[19] Wang Jun, Liu Wei, Sun A X, et al. Learning hash codes with listwise supervision[C]//Proceedings of the Computer Vision (ICCV), Sydney, Australia, 2013: 3032-3039. [本文引用:1]
[20] Zhang Dell, Wang Jun, Cal Deng, et al. Self-taught hashing for fast similarity search[C]//Proceedings of the International ACM SIGIR Conference on Research and Development in Information Retrieval, Geneva, Switzerland , 2010: 18-25. [本文引用:2]
[21] Zhu Xiao-feng, Huang Zi, Cheng Hong, et al. Sparse hashing for fast multimedia search[J]. ACM Transactions on Information Systems (TOIS), 2013, 31(2): 9. 1-9. 24. [本文引用:1]
[22] Lin Guo-sheng, Shen Chun-hua, Suter D, et al. A general two-step approach to learning-based hashing[C]//Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 2013: 2552-2559. [本文引用:1]
[23] Russell B C, Torralba A, Murphy K P, et al. LabelMe: a database and web-based tool for image annotation[J]. International Journal of Computer Vision, 2008, 77(1-3): 157-173. [本文引用:1]
[24] Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images[R]. Toronto, 2009. [本文引用:1]
[25] Vedaldi A, Fulkerson B. VLFeat: an open and portable library of computer vision algorithms[C]//Proceedings of the International Conference on Multimedia, Firenze, Italy, 2010: 1469-1472. [本文引用:1]
[26] Philbin J, Chum O, Isard M, et al. Object retrieval with large vocabularies and fast spatial matching[C]//Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Minneapolis, Minnesota, 2007: 1-8. [本文引用:1]
[27] Liu Wei, Wang Jun, Kumar S, et al. Hashing with graphs[C]//Proceedings of the International Conference on Machine Learning (ICML-11), Bellevue, Washington, 2011: 1-8. [本文引用:1]