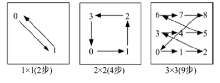
红外微扫描成像技术通过对同一场景进行多次采样, 从多幅相互之间有亚像素位移的时间序列低分辨率图像复原重建出高分辨率图像。红外微扫描成像系统主要采取1× 1、2× 2和3× 3这三种工作模式^[13], 如图1所示。微扫描模式决定了探测器上图像的位移周期和微扫描轨迹。每种微扫描模式都有不同的扫描轨迹以及扫描步数, 随着微扫描步数的增加, 微扫描系统的空间分辨力也会随之提高。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 微扫描成像系统工作模式Fig.1 Working mode of micro-scanner imaging system

采用数值分析方法可以分析微扫描模式与调制传递函数(MTF)之间的关系, 从而得到微扫描成像质量评价结果。

实际红外微扫描超分辨成像系统涉及光、机、电、算、软等部分组成, 其系统组成如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 微扫描超分辨成像系统构成Fig.2 Architecture of micro-scanner imaging system

从图2可知, 微扫描超分辨成像系统主要由图像采集硬件系统和软件处理系统两部分构成。本文主要描述微扫描超分辨成像硬件部分微位移序列图像获取方法和软件部分超分辨率图像重建算法。

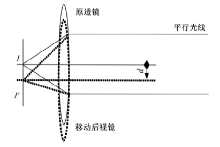
红外微扫描成像系统的光学微位移机构可实现相对于成像器件焦平面探测器的微位移。现有的光学微扫描实现方式归结起来主要分为机械平移法、平板旋转法和摆镜法。其中机械平移透镜主要采用压电陶瓷驱动和电机驱动的方式。机械平移透镜微扫描原理如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 机械平移透镜微扫描原理Fig.3 Principle of micro-scanner based on mechanics translation lens

由于透镜的离轴位移量很小, 因此产生的像差很小并且无像旋。此外, 微扫描透镜和二轴微扫描位移台的质量可能会对系统性能产生影响, 设计质量轻的单片透镜作为微扫描透镜是解决该问题的办法之一。

由于需要精确移动的微位移很小(亚像素), 其微扫描幅度为μ m级, 小于对应探测器的探测元间距, 需要很高的精度, 主要有两个方面的难点^{[14, 15]}:需要保证将图像从一个位置移到下一个位置时间上的精确性和微位移自身的精确性。

通过采用数值分析方法分析得到微扫描模式与调制传递函数(MTF)之间的关系, 发现2× 2微扫描模式对MTF的贡献率最大, 实用价值最高, 故通过电机驱动在2× 2模式下每次移动半个像元。其中, 探测器有效像素为320× 256, 像元间距离为30 μ m, 像面大小为9.6 mm× 7.68 mm。

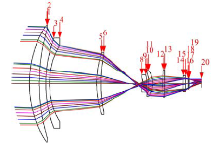
红外微扫描光学系统设计结构如图4所示, 其中总长为391 mm, F数=2, 焦距f=240 mm; 第6片透镜偏心扫描, 幅度为25 μ m, 质量约为9.66 g。因为要旋转微位移驱动控制器, 前、后空间分别为22 mm和30 mm。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 微扫描成像光学系统设计Fig.4 Optical system design of micro-scanner imaging

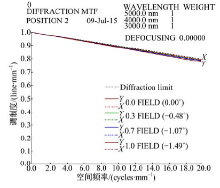
利用光学设计软件CODE V对微扫描光学子系统的MTF进行评价, 结果如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 微扫描成像光学系统MTFFig.5 MTF of micro-scanner imaging system

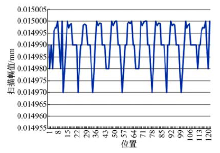
此外, 选取像方不同视场下的121个位置, 通过计算扫描幅值均控制在半个像元(即15 μ m)以内, 幅值变化情况如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 不同视场成像位置扫描幅值Fig.6 Scan amplitude of image space of different field

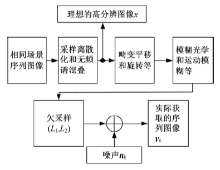
如果低分辨图像序列间存在亚像素位移关系, 并能够确定或估计低分辨率序列图像与重建后的高分辨率图像之间的关系, 就可以建立观测模式进行超分辨重建^[16]。光电成像系统实际成像时由于受像差、衍射极限等因素的影响造成图像的退化, 整个退化模型的构建如图7所示^[17]。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 图像退化模型的构建Fig.7 Construction of image deterioration model

在图7中, 假设理想目标高分辨率图像的大小为N=L₁N₁× L₂N₂, 每幅低分辨率图像的大小为M=N₁× N₂, 其中L₁ 和L₂ 表示观测模型中水平方向和垂直方向的欠采样算子, 则在高于奈奎斯特频率处从一连续带宽限制信号里采样得到的理想非退化图像的向量表示形式为x=[x₁, x₂, …, x_N ]^T, 第k幅低分辨率图像的向量表示形式为 yk=[yk, 1, yk, 2, …, yk, M]T, 这里k∈ [1, P], 图像退化模型经空间域离散化后, 对于同一场景下的k幅序列低分辨率图像, 可由一幅高分辨图像经过几何形变、模糊、欠采样和噪声等一系列的降质或者退化过程产生, 这样可以用如下表达式表述观测模型:

yk=DBkMkx+nk, 1≤k≤p(1)

式中:M_k表示大小为L₁N₁L₂N₂× L₁N₁L₂N₂ 的畸变矩阵; B_k 表示大小为L₁N₁L₂N₂× L₁N₁L₂ N₂ 的模糊矩阵; n_k表示图像噪声。

POCS算法是目前超分辨率复原重建中应用最为广泛的算法之一, 该算法基于集合理论。采用POCS方法进行图像的超分辨重建需要解决3个问题:把关于解的若干限制条件解释为包含解的凸集 Ci;确定每个凸集的投影算子 Pi;为投影算子选择合适的松弛参数 λi进行迭代投影。

首先, 设待复原重建的高分辨率图像 f是Hilbert空间H中的一个元素, 对于m个已知的约束信息, 就存在m个对应的闭凸集C_i, 其中i∈ [1, m], 所求的f需要满足以下条件:

f∈C0=⋂i=1mCi(2)

然后, 把P₀ 个P_i标记为投影算子分别投影到凸集C_0 和C_i, 封闭的凸集与它们各自的投影算子P_i产生投影序列如下:

f(k+1)=PmPm-1…P1f(k), k∈[1, m](3)

最后, 为了加速算法的收敛速度, 引入松弛算子 λi将式(3)表述为以下形式:

f(k+1)=TmTm-1…T1f(k), k∈[1, m](4)

式中：

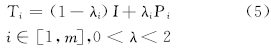
利用POCS算法将式(1)实例化为如下形式:

gl(m1, m2)=∑(n1, n2)f(n1, n2)hl(m1, m2; n1, n2)+ηl(m1, m2)(6)

式中:g_l(m₁, m₂)表示第l帧低分辨率图像; f(n_1, n_2)表示原始高分辨率图像; h_l(m₁, m₂; n₁, n₂)表示第l帧图像的PSF; η _l(m₁, m₂)表示第l帧图像的噪声。

利用微扫描多帧序列低分辨率图像重建高分辨图像, 可以定义数据一致性约束集合如下:

Cm1, m2, l={f(n1, n2, k)∶|r(f)(m1, m2, l)|≤δ0(m1, m2, l)}(7)

式中：

r(f)(m1, m2, l)≜g(m1, m2, l)-∑(n1, n2)f(n1, n2)hl(m1, m2; n1, n2)(8)

r^(f)(m₁, m₂, l)代表和约束集合中任意一点f相关的残差; δ ₀(m₁, m₂, l)表示先验界限, 代表统计置信水平。

高分辨率图像任意一点 x(n1, n2, k)在集合 Cm1, m2, l上投影 pm1, m2, l[x(n1, n2, k)]定义为式(9):

pm1, m2, l[x(n1, n2, k)]=x(n1, n2, k)+[r(x)(m1, m2, l)-δ0(m1, m2, l)]×[∑x1∑y1h2(m1, m2; x1, y1)]-1× h(m1, m2; n1, n2, l), r(x)(m1, m2, l)> δ0(m1, m2, l)x(n1, n2, k), -δ0(m1, m2, l)≤ r(x)(m1, m2, l)≤δ0(m1, m2, l)x(n1, n2, k)+[r(x)(m1, m2, l)+δ0(m1, m2, l)]×[∑x1∑y1h2(m1, m2; x1, y1)]-1× h(m1, m2; n1, n2, l), r(x)(m1, m2, l)< -δ0(m1, m2, l)(9)

基于POCS超分辨图像重建算法的流程为:

(1)对超分辨率图像进行预估计完成参考帧构造, 利用式(9)投影算子重复进行投影迭代, 就可以求解超分辨率图像的估计值。

(2)利用运动估计算法估计相对参考帧的运动补偿参数。

(3)对参考帧进行不断修正直到获得可以接受的重建结构, 当达到最大迭代次数或者两次迭代之间的误差小于设定的阈值终止迭代, 所得到的迭代解为POCS方法的最优估计解。

为了最大限度地保留低分辨原始图像边缘细节信息, 在降低噪声干扰的同时保留有价值的高频信号, 提出一种改进的POCS复原重建算法。

算法具体步骤如下:

Step1构造参考帧。输入第一幅待分辨率图像, 利用双线性插值法构造一帧高分辨率图像Ref。

Step2设置初始参数。手动设置迭代次数 N,初始值为0。

Step3运动参数估计。利用四参数仿射变换模型(10)计算低分辨率序列图像间的运动参数。

x'y'=xy+ kcos(α)sin(α)-sin(α)kcos(α)xy+d1d2(10)

式中:(x', y')和(x, y)表示图像像素点位置; k表示图像缩放系数; α 表示图像旋转角度; d₁表示水平位移; d₂表示垂直位移。

Step4投影和灰度修正。利用基于边缘检测的PSF算子修正参考帧的像素值。

Step4.1利用POCS投影算子(9), 通过PSF将低分辨率序列图像中像素点投影到参考帧上。

Step4.2基于边缘检测的PSF算子(11), 计算参考帧图像中像素点的灰度估计值。

PSF=exp(-λd)PSF0(11)

式 中:λ 表示约束正则化系数, 可以用于调节exp(-λ d)的数值衰减速率; d表示像素点到图像边缘的空间距离; PSF₀=exp[-(x-x₀)²+(y-y₀ )²/2]。

Step4.3与序列低分辨率图像中的相同区域位置的实际灰度值进行比较, 若超出误差范围, 则对参考帧像素点的灰度值进行修正。

Step5判断是否满足迭代终止条件。若满足, 则退出迭代步骤; 否则返回Step4。

Step6采用基于K-SVD字典学习方法^[18]对POCS估计图像进行去噪声处理。

实验测试采用的操作系统为Windows 7旗舰版64位SP1; 处理器为Intel Core i7-4790K @4.00 GHz四核; 内存为16 GB(DDR3 1333 MHz); 算法开发工具为Matlab Primer R2015a。

仿真实验采用大小为480× 480像素的原始高分辨图像, 如图8(a)所示。首先, 经过加入随机噪声和模糊、降采样因子为2的处理, 得到4幅240× 240像素的低分辨率序列图像。低分辨率序列图像的位移差为0.1, 角度差为0.005, 以此来模拟附有噪声的低分辨率图像序列。然后, 分别采用不同的算法进行序列图像的超分辨率重建, 结果如图8(b)(c)(d)(e)所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 模拟图像退化SRIR实验结果Fig.8 SRIR experimental results of simulating of image deterioration process

从图8可以看出, 双线性插值法难以对图像噪声进行处理, 一般POCS算法虽然对噪声有一定抑制作用但图像边缘处仍然有明显的梯度效应, 本文算法对噪声有明显抑制作用并较好地复原出图像边缘细节信息。为了更客观地评价重建图像质量, 采用PSNR和SSIM两个指标对不同算法的实验结果进行对比, 如表1所示。

表1

Table 1

表1(Table 1)

表1 模拟图像退化过程SRIR实验数据对比 Table 1 Data comparison of SRIR based simulating 算法 PSNR SSIM 双线性插值 24.6 0.7979 一般POCS 21.7 0.8535 本文算法 21.9 0.9156

表1 模拟图像退化过程SRIR实验数据对比 Table 1 Data comparison of SRIR based simulating

表1中结果表明:本文算法具有更好的图像重建效果。为了进一步验证算法在实际拍摄中能否取得较好的效果, 采用非制冷红外成像仪在2× 2微扫描工作模式下每次移动半个像元, 采集获得原始、水平和垂直位置的4幅微位移低分辨率序列图像, 图像大小为320× 256像素。分别采用不同的重建算法对序列图像进行超分辨率重建, 由于实际拍摄的图像没有理想高分辨率图像作参考, 为了更直观地比较超分辨重建结果,

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 实际拍摄红外图像SRIR实验结果Fig.9 SRIR experimental results of real infrared images

将图像放大4倍进行显示。从图9中可以看出, 本文算法重建图像的边缘细节更为清晰。

如图10所示, 通过分析低分辨图像和本文算法重建的高分辨图像二维频谱可以看出, 本文算法对噪声也起到了较好的抑制作用。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 高、低分辨率图像二维频谱对比Fig.10 Comparison of two-dimensional spectra beween high and low resolution image