在基于快速搜索和发现密度峰值的聚类算法中, 假定类簇中心周围节点的局部密度一般都低于该中心的局部密度, 并且与具有更高密度的节点的距离都较大。首先计算每一个数据节点i局部密度ρ _i和该点到更高局部密度的节点的最短距离δ _i, 并根据ρ _i和δ _i画出决策图, 在决策图里面找到类簇中心; 其次, 在找到类簇中心后, 根据每一个节点的最近更高局部密度节点的类别确定其所属簇类中心。由于该算法对于多种类型的数据显示出了良好的适用能力和极高的运行效率, 所以将其引入到复杂网络的社区划分问题中, 但是这里面有两个问题需要解决。首先在原算法中需要计算不同节点之间的距离, 而在复杂网络中, 一般给出的是节点之间的连接情况, 分有权和无权两种。而对于没有连接的节点, 如果认为它们之间的距离全部为无穷大, 则距离矩阵中将出现大量的无穷大, 这样一是不符合实际情况, 另外也不利于得到好的分类结果。第2个需要解决的问题就是原聚类算法只能解决标准划分的社区分类结果, 而无法处理包含重叠节点的社区分类问题。对于第1个问题, 本文通过设计一种距离矩阵生成算法进行解决; 对于第2个问题, 本文不再是将剩余的待划分节点都划分到其最近更高局部密度节点所在的类簇中, 而是计算各个节点属于各个类簇中心的概率, 最后, 根据得到的概率值确定节点是否为重叠节点且应属于哪个类簇。算法流程如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于概率密度的社区发现算法流程图Fig.1 Flow chart of overlapping community detection method based on density peaks

在该算法中, 需要用到不同节点之间的距离, 即距离矩阵。然而在复杂网络中, 已知的是网络节点之间的连接情况, 即不同节点之间是否连接(无权)或是连接的强度(有权)有多少, 无法直接给出节点之间的距离。为了叙述简便, 本小节以无权形式进行说明, 有权的情况也完全适用。首先, 针对无权网络, 如果直接将没有连接的节点之间的距离看成是无穷大, 则可以直接生成距离矩阵。但是这样做矩阵中将出现大量的无穷大, 无法得到好的聚类结果。Floyd算法^[14]能够处理无权图或加权图的最短路径问题, 但是该算法在用于无权图时, 得到的最短路径长度都是整数, 并且该长度包含了大量的重复值。若用Floyd算法求得的距离来进行聚类, 决策图中的类簇中心并不明显, 有时甚至找不到类簇中心或所有节点都是类簇中心, 这不符合实际情况。

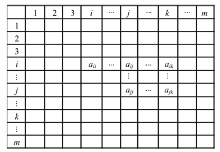
本文也希望通过节点之间的连接情况来定义它们之间的距离。但是与Floyd算法通过求两点之间的路径长度来定义它们的距离不同, 本文考虑的是两个节点之间的连接强度, 所得到的距离不是整数而是实数。设矩阵A_{m× m}={a_ij}为已知的连接矩阵, 其中a_ij={0, 1}, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 矩阵AFig.2 Matrix A

当a_ij=1时, 可以认为i、j两个节点之间的直接连接强度为1, 而当a_ij=0时, 则认为i、j两个节点之间的直接连接强度为0。而本文认为, 两个节点之间除了直接连接之外, 还应该有间接连接。比如, 当a_ik=a_jk=1, 意味着i、k节点之间和j、k节点之间的连接强度都为1, 那么i到j可以通过i到k然后再k到j实现。因此, 可以更新a_ij为:

aij=α·aij+β·∑kaik·akj(3)

式中:等号右边第一项表示惯性项; 第二项表示间接连接项; α 和β 表示惯性因子和间接连接因子, 均为给定常数, 并令α +β =1。此过程可以迭代进行若干次, 因此, 记 A=A0={aij0},则式(3)更新为:

aij(t+1)=α·aij(t)+β·∑kaik(t)·akj(t)(4)

随着迭代的进行, 矩阵中的元素越来越大, 因此需要进行规范化, 于是定义一个新的矩阵系列 B(t)={bij(t)},公式再次更新为:

bij(t)=aij(t)maxk, s(ak, s(t))(5)

aij(t+1)=α·bij(t)+β·∑kbik(t)·bkj(t)(6)

假设迭代T次之后停止, 令距离矩阵为 D={dij}, 则有dii=0, dij=1/aij(T)。

在得到距离矩阵后, 接下来可以与基于快速搜索和发现密度峰值的聚类算法一样, 得到所有节点的局部密度和该点到更高局部密度最近点的距离, 并画出相应的决策图, 得到类簇中心。

因为需要确定重叠社区节点, 所以找到类簇中心后, 不能再按原方法进行划分, 而是要计算各个节点属于各个类的概率。算法的主要思路是每个节点不确定属于哪一类, 而是对所有类别分配一个概率。概率的计算由比该节点局部密度大的最近邻N_NEIB个节点的概率向量加权确定。具体方法如下:

假设得到了 c个簇类中心, 并假定每个簇类中心只能属于一个类别。设节点i属于不同类别的概率为 pi={pi1, pi2, …, pic}, 第j个簇类的中心节点编号为n_j, 则取 pnj, j=1, pnj, k=0(k≠j), 这样首先确定了所有簇类中心的概率向量。对于其他节点, 从局部密度最大的节点开始计算其概率向量。设该节点编号为i, 假定比节点i局部密度大的节点个数为 N_Li个, 并按和该节点的距离从小到大排序, 记其编号为 i1, i2, …, iN_Li, 则节点i的概率向量按如下公式确定:

pi=∑j=1n0wijpij(7)

式中: n0=min{N_NEIB, N_Li}; 权值w_ij满足:

wij=1/di, ij/∑k=1n01/di, ik(8)

当得到所有节点的概率向量之后, 对于节点i, 如果r=argmax_s{p_{i, s}, s=1, 2, …, c}, 那么节点i就属于r社区。然而, 在现实网络中, 节点不是只能属于某一个特定的社团, 而是可能同时被划分到多个社团中。因此需要对重叠节点进行判断。如果某节点已经被划分到社区c中, 但是属于社区s的概率与属于社区c的概率值相对比较接近, 则可以认为该节点同时属于社区s。例如, 节点i属于社区r, 其概率为p_{i, r}, 如果p_{i, s}/p_{i, r}> ζ , ζ 为可调参数, 那么i也属于社区s, 即节点属于社区s与属于社区r的概率差不多时, 就认为节点i既属于社区s, 又属于社区r, 则节点i就是重叠节点。

选取文献[15]中所使用的5组实验数据进行了试验。其中空手道俱乐部(Karate)网络描述的是美国一所大学空手道俱乐部成员之间的社会关系, 包括34个节点和78条边, 边代表两个成员除了来俱乐部之外经常联系^[17]。海豚关系网络(Dolphin)是Lussseau等^[18]对一个宽吻海豚群体观察7年所构造的。该网络共有62只海豚, 边数共有159条, 分成两组, 边代表两个海豚间接触相对频繁。科学家合作网络(Net-Science)将每个科学家看作节点, 若科学家之间有合作发表文章或者合作研究等, 则这些有合作的科学家之间就有边相连^[19]。网络中共有1589个科学家, 有2742条边, 但其中最大连通子图只有379个科学家, 914条边。电力系统数据集(Power)是美国西部电力网络, 节点为发电厂、变压器或变电站, 每个节点都认为是无区别节点, 网络中的边是高压输电线和变压器支路^[20]。该网络有4941个节点, 6594条边。在词联想网络(Word-Association)中, 每个节点代表一个词语, 如果两个词语之间有某种联系, 则这两个词语所对应的节点之间就存在一条边, 有7205个节点, 31784条边^[21]。5组数据的统计情况见表1。

表1

Table 1

表1(Table 1)

表1 五组实验数据 Table 1 Overview of 5 datasets 数据集 节点数 边数 边数/节点数 Karate 34 78 2.29 Dolphin 62 159 2.56 Net-Science 379 914 2.41 Power 4941 6594 1.33 Word-Association 7205 31784 4.41

表1 五组实验数据 Table 1 Overview of 5 datasets

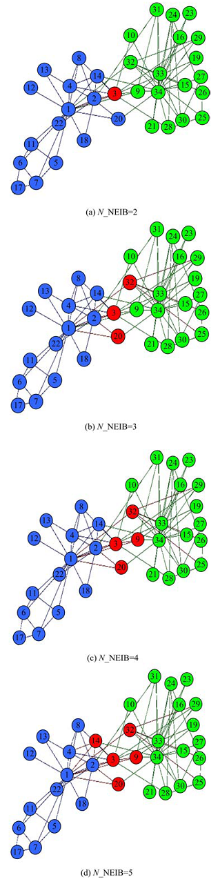
鉴于节点数较多的网络很难看清, 所以只选取了Karate和Dolphin两组数据展示了得到的社区划分结果。首先, 如果不考虑重叠节点, 对于N_NEIB参数不同选取的两组数据都得到了相同的结果, 并与原始文献的划分一致。

图3为当N_NEIB分别取2、3、4、5时Karate网络的划分结果, 红色代表重叠节点。当N_NEIB取2时, 只有节点3为重叠节点。图中可见节点3与两个社团的连接都相对比较紧密, 因此将其划分为重叠节点是合理的。当N_NEIB取3时, 节点3、20、32被划分为重叠节点。其中节点20、32与类簇中心节点1和34都有直接的联系, 因此将它们划分为重叠节点也是合理的。当N_NEIB取4时, 将节点3、9、20、32作为重叠节点。其中节点9是簇类中心节点34的弱支持者, 在该社团分裂之后, 节点9就加入到了节点1所在的社团中。当N_NEIB取5时, 进一步增加了节点14为重叠节点。节点14与节点20类似, 都与簇类中心有比较直接的联系。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Karate网的重叠社区划分结果Fig.3 Overlapping community partition result of Karate net

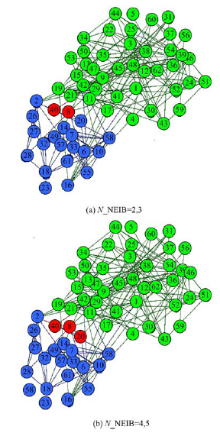
类似的, 图4给出了N_NEIB不同取值时Dolphin网络的划分结果, 红色代表重叠节点。图4(a)中, 重叠节点为节点7和节点39; 图4(b)中, 重叠节点增加了第19号节点。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 Dolphin网的重叠社区划分结果Fig.4 Overlapping community partition result of Dolphin net

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 划分结果的EQ值与N_NEIB参数的关系Fig.5 Relationship between EQ value and N_NEIB parameter

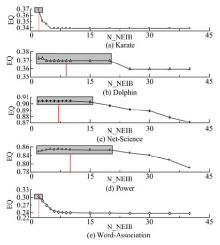
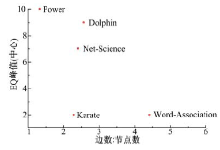
为分析N_NEIB参数对算法性能的影响, 分别取值为2、3、4、5、10、15、20、25、30、35、40, 对结果进行比较, 结果如图5所示。图5中的深色框代表的是EQ的峰值或是其值较高的一个平台。经过观察发现, EQ的峰值(中心)所处位置与该网络的密度, 即边数/节点数关系密切。图6给出了两者之间的关系。由图6可以发现, 除了Karate之外, 其余几个点的EQ的峰值(中心)位置与网络密度呈现出了很强的负线性相关性质。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 EQ的峰值(中心)位置与边数:节点数的散点图Fig.6 Scatter diagram for relationship between EQ peak(center)and Edge/Node

将得到的实验结果与文献[14]中的给出的GCE、COPRA、LFM、CFinder四种方法的结果进行了对比, 结果如表2所示。由表2中可以看出, 在空手道网络中, LFM算法的EQ值最高, 本文提出的OCDMDP算法要高于其他3个算法; 在海豚关系网络中, LFM算法的EQ值也优于其他4种对比算法, OCDMDP算法与其余3种算法的EQ值相差不大。而对于Word-Association网络, 本文算法的划分结果虽然没有GCE算法的划分结果好, 但是和它的EQ值也比较相近, 而且比LFM和CFinder算法的划分效果要好得多。在另外两组数据中, 本文OCDMDP算法的EQ值都有明显的优势, 如在Net-Science网络中, DGDMP算法的EQ值比其他4种中最好的COPRA算法高出20.1%, 而在Power网络中, OCDMDP算法的结果比其他算法中最好的COPRA算法高出16.3%。从平均值来看, 4种比较算法表现最好的是COPRA算法的0.507, 而OCDMDP算法为0.541, 比COPRA的结果提高了6.71%。综上所述, COPRA算法在不同数据集上的综合表现要优于其他4种算法。

表2

Table 2

表2(Table 2)

表2 EQ值的比较结果 Table 2 Comparison results of EQ values GCE COPRA LFM CFinder OCDMDP Karate 0.294 0.184 0.402 0.186 0.339 Dolphin 0.372 0.373 0.497 0.361 0.367 Net-science 0.724 0.753 0.743 0.629 0.904 Power 0.308 0.718 0.621 0.158 0.835 Word-Associate 0.270 ~0 0.224 0.022 0.255 Average 0.394 0.507 0.487 0.271 0.541 注:黑体的数值为每个数据集的最优EQ值。

表2 EQ值的比较结果 Table 2 Comparison results of EQ values