目前, 基于图像内容的认证技术作为针对数字图像传输的有效安全方法, 已经成为图像领域的研究热点^[1]。在真实的网络传输环境中, 数字图像容易遭受类似裁剪、替换等针对图像指定内容的人为篡改攻击, 而在数据的传输中, 特别是在无线环境下, 会受到诸如距离、地形、空间环境、收发双方设备功率不足等因素所产生的噪声干扰, 进而造成存在一定程度的失真。对于噪声干扰造成的图像数据改变通常被认定为是可接受的, 而对于人为篡改造成的改变则被认定为是不可接受的。对于需要区分噪声干扰和人为篡改的图像认证算法, 其要求对人为篡改具有一定的敏感性, 而对于噪声干扰则要求具有一定的鲁棒性, 这种对噪声干扰有一定鲁棒性的技术通常为基于半脆弱水印算法的图像认证技术, 其内容是指在图像内容能够基本保留的前提下, 允许作品遭受一定程度的噪声干扰而失真, 但对于遭受恶意篡改而导致内容发生改变的图像则不允许通过认证。该算法能够在容忍一定程度的噪声干扰, 并检测图像内容的人为篡改^{[2, 3, 4, 5, 6, 7]}。朱光等^[8]将原图像由RGB信号转换成亮度和色差信号, 并提取SURF在亮度分量上的特征点, 根据其主方向构造描述向量, 并分解为两个子分量, 通过计算子分量与法向量之间的夹角, 比较夹角的大小关系来构造水印, 最后将其嵌入至图像的空域中。该方法在椒盐噪声条件下能够有效识别图像篡改, 但在其他的噪声环境下则不能运作。Wang等^[9]通过引入子块组概念, 使用特定区域块结合Slant变换直流量化原理完成水印的嵌入, 并在认证过程中使用噪声过滤策略完成对图像篡改与噪声干扰的区分, 从而实现基于图像内容的篡改检测。该算法对图像压缩有很好的抵抗性, 但是对类似改变图像对比度的噪声干扰方面检测效果较差; Preda^10]利用多重量化系数来嵌入水印, 并通过DWT变换, 来控制水印的鲁棒性, 最后利用篡改检测函数来进行图像认证, 该算法对于图像压缩的鲁棒性效果较好, 但是对于其他诸如高斯噪声和滤波操作的鲁棒性较差, 因此使用起来有很大的局限性。

本文提出了一种高鲁棒性的图像内容认证算法。首先, 利用视觉注意模型对原图像进行显著图提取, 并对显著图进行NMF变换以降低显著图的维度。然后利用混沌加密算法对降维后的显著图进行加密, 并将加密后的降维显著图作为数字水印利用DCT变换嵌入到原图像的低频分量中, 在接收端, 利用DCT逆变换对接收图像进行水印提取, 并通过混沌解密算法进行解密以得到原水印接着, 对接收图像进行显著图提取, 并与所提取的水印进行对比, 得到二者的差分图像矩阵。最后对差分矩阵求基于像素值分布和像素位置分布的差分系数, 再进行联合加权并与设定的阈值进行比较, 得到最终认证结果。

对于一幅图像的不同部分, 其信息量的分布也不尽相同, 因此可以基于图像信息的分布提取其显著性模型, 类似方法中比较著名的有ITTI模型^[11], 其利用特征整合理论, 依据中心围绕机制和低级特征对比标准化方法构造显著图。

本文采用了最大熵算法来提取图像中的感兴趣区域, 最大熵理论通常用于图像分割^[12], 其原理是把图像分为信息密度高的内容区域和信息密度低的背景区域, 在同一区域内熵值的波动幅度较小, 而不同区域间熵值有很明显的差异, 又根据Shannon提出的熵定义:

H(A)=-∑i=1np(i)logp(i)(1)

由式(1)可知, 当内容区域与背景区域熵值的波动幅度都相对较小时, 图像的信息熵达到最大, 通过自动调整阈值使内容区域与背景区域的熵值之和达到最大时, 图像的内容与背景分割达到最优。相比ITTI模型, 此模型融合了基于局部能量特征的最大熵模型来计算图像每一像素点的显著度, 并将其表示为一幅灰度图, 即显著图。

对于提取出来的显著图, 本文利用基于非负矩阵分解(NMF)的稳健哈希方法^[13]。NMF有两个特性:一是基的叠加特性使NMF反映图像的局部特征, 可以有效分辨基于图像内容的篡改; 二是几何变换的结果以独立同分布噪声的形式叠加在NMF矢量上, 很容易将其滤除。相比于传统算法, NMF分解算法有运算速度快、占用存储空间少等优点。

设A是m× n的非负矩阵, 对A进行NMF分解得到基矩阵W和系数矩阵V,则有:

A≈WV, W∈Rm×k, V∈Rk×n, k< < m, n(2)

此时, 可用基矩阵与系数矩阵的乘积WV近似代替矩阵A, 从而得到基于图像视觉注意模型的降维显著图。在本文中, 对于256× 256的测试图像, 取k=8, 这里通过引入峰值信噪比(PSNR)来判定两幅图像的差异情况, 峰值信噪比是一个表示信号最大可能功率与影响其表示精度的干扰功率的比值的术语, 由于许多信号的波动范围相当大, 因此峰值信噪比常用分贝(dB)表示, 其公式为:

PSNR=10lg2552MSE(3)

式中:MSE为两幅图像之间的均方差。

若两个 m×n的RGB图像I和K, 如果二者噪声近似, 那么它们的均方差定义为:

MSE=13mn∑i=1m∑j=1n∑k=13‖I(i, j, k)-K(i, j, k)‖2(4)

由式(3)(4)可知, 若干扰噪声对图像的改变越大, 则MSE值越大, PSNR的值越小, 基于上述原理测得原显著图与降维显著图差异程度如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 原显著图与降维显著图差异程度比较Fig.1 The difference between original saliency map and dimensionality reduction saliency map

由图1可以看出, 当k=8时, PSNR=80.6494, 可见降维显著图相比于原显著图几乎完全一样, 失真情况相当微小, 但总像素却由256× 256降为256× 8× 2, 即为原显著图的1/16, 因此, 基于NMF分解的图像降维方法在失真程度允许的情况下, 可显著降低图像的大小, 从而可以使其作为数字水印顺利地嵌入到原图像中。

对于由NMF降维得到的基矩阵W和系数矩阵V, 经过合并重排之后可获得64× 64的变换矩阵C, 对矩阵C进行混沌加密^[14], 得到加密后的置乱矩阵, 之后在置乱矩阵中加入汉明校验码, 以提高水印的鲁棒性, 最后对置乱矩阵利用DCT-SVD变换^[15]嵌入原图像的低频系数中, 在此, 本文选择一张256× 256的Lena彩色图像和64× 64的加密水印, 其测得原图像与嵌入水印后图像差异程度如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 原图像与嵌入水印图像间差异程度比较Fig.2 The difference between original image and watermarked image

由图2可以看出, 相比于原图像, 基于DCT-SVD嵌入的水印, 几乎不会引起图像的失真。同时由于DCT-SVD变换对噪声和篡改有很好的鲁棒性, 因此可以保证在接收端提取水印的完整性。

首先, 本文通过DCT-SVD逆变换提取经过加密的数字水印, 再利用混沌解密算法可分离出基矩阵W和系数矩阵V, 进而可以得到降维显著图WV, 之后利用视觉注意机制提取接收图像的显著图A_receive, A_receive 与WV相减可得到差分图像A_sub, 进而可通过基于像素值和基于像素位置差异程度衡量算法来认证图像是否遭受人为篡改。

由于图像的人为篡改是对图像信息恶意修改, 因此往往把图像某一部分的信息进行集中改变, 而图像在噪声信道上受到的干扰, 以及对图像进行的有损压缩是对图像信息全方位、无重点的改变, 前者会造成图像信息分布的显著变化, 而后者则对图像信息分布的改变不大。因此本文利用Lorenz曲线衡量像素值与像素位置的差异程度, 从而获得图像像素值分布的联合权值。

本文使用了一种基于Lorenz曲线的差异算法衡量像素值分布的差异程度。Lorenz曲线在经济学方面广泛应用, 其主要功能是计算衡量国家人口间贫富差距的基尼系数。在本文中结合类似的使用方法, 计算像素值间和像素位置间的差异程度。在像素值差异程度的计算方面, 首先对差分图像中的所有像素点按照像素值的大小进行升序排列, 并求得像素点的个数V和所有像素点的像素值之和N。对于第i个像素点, y(i)表示不小于i点的个数, x(i)表示不小于i点的所有像素点之和, 以y(i)/V作为纵坐标, x(i)/N作为横坐标, 求得Lorenz曲线如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 Lorenz曲线示意图Fig.3 The diagram of Lorenz curve

图3中, 若图像像素值的差异程度越大, 则S₂的面积越大, 反之则越小, 用差异参数φ _L对图像像素值的差异程度进行评估, 其计算公式为:

φL=S2/(S3+S2)(5)

φ _L值越大说明图像像素值差异程度越大, 图像越有可能被人为篡改。

由于人为图像篡改往往只针对于一片或少数几片相对集中的区域进行, 而其他区域则不做任何改动, 因此生成的差分图像会表现出像素值较高的点聚集在集中的区域中。而由于噪声引起的图像信息的改动会随机分布于图像中的各个部分, 因此噪声干扰不会存在区域聚集性, 反而会有很好的均匀性。由此理论, 本文通过对差分图像 Asub进行随机分块, 以获得差分图像在某一集中区域内所有像素的像素值之和, 如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 Lena图被随机分割成25个32× 32的子图像块Fig.4 Lena image is divided into 25 32× 32 pixel sub-image blocks

在本文中, 设区块i中所有像素的像素值之和为T_i, 则参考图3的Lorenz曲线原理, 用差异参数φ _T对图像每一区块中像素值总和的差异程度进行评估, 其公式为:

φT=n2∑i=1nTi-∑k=1n∑i=1kTin2∑i=1nTi(6)

式中:n为随机分块的图像块的数量, 这里φ _T值越大, 说明图像区块之间的像素值总和差异程度越大, 在图像显著图中改变区域的聚集性越明显, 图像越有可能被人为篡改。

通过对基于图像像素值分布的差异参数φ _L和基于图像像素位置分布的差异参数φ _L进行联合加权, 加权公式为:

φ=φL×φT×λ(7)

式中: λ 为补偿参数, 本文取λ =10。

通过联合加权, 使得基于图像像素值分布的差异参数与基于图像像素位置分布的差异参数相结合, 从而能够有效区分有规律的人为篡改和无规律的噪声干扰所造成的图像信息的更改。

为了测试水印本身的鲁棒性, 本文引入归一化相关系数(NC)来测量嵌入的水印图像与提取的水印图像二者间的差异度, NC值越接近于1, 表明两幅图像差异度越小, 相关性越大。表1显示了本文方法与其他DCT变换方法^{[16, 17]}间的差异度比较。

表1

Table 1

表1(Table 1)

表1 不同水印嵌入算法下NC值的比较 Table 1 Comparison of NC values under different watermarking embedding algorithms 算法 本文算法 文献[16]算法 文献[17]算法 对比度增强 均值滤波 泊松噪声 椒盐噪声(2%) 椒盐噪声(5%) 高斯噪声(2%) 高斯噪声(5%) 0.9913 0.9937 0.9884 0.9939 0.9821 0.9689 0.9493 0.9558 0.9914 0.9811 0.9295 0.8612 0.8937 0.8923 0.9338 0.9909 0.9754 0.9289 0.8420 0.8116 0.6814

表1 不同水印嵌入算法下NC值的比较 Table 1 Comparison of NC values under different watermarking embedding algorithms

由图1可以看出, 相比于其他DCT水印嵌入算法, 本文算法有着更高的 NC值, 因此说明本文算法在不同的噪声干扰情况下, 有更好的鲁棒性。此外, 本文模拟噪声干扰和人为篡改得到两幅Lena图像, 并分别得到两幅图像基于视觉注意模型的差分图像, 然后计算基于图像像素值和图像像素位置分布的差异程度参数, 最后进行联合加权, 结果如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
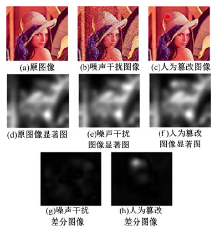	图5 噪声干扰图像与人为篡改图像测试效果对比Fig.5 The result between noise interference image and artificial tampering image

由图5可以看出, 相比于噪声干扰图像, 人为篡改图像的联合加权系数 φ显著增大, 因此, 可以设定合适的阈值来区分噪声干扰图像与人为篡改图像。表2更加详细地列出了在多种不同条件下, 用Lena, Baboon和Boats三张常用图像处理测试图像所得的实验结果。

表2

Table 2

表2(Table 2)

表2 不同测试条件下联合加权系数的比较 Table 2 Comparison of joint weighted coefficients under different conditions 图像篡改类型 Lena Baboon Boats 对比度减弱 对比度增强 均值滤波 图像压缩 椒盐噪声 高斯噪声 裁剪 替换 0.9831 1.0034 1.2376 1.1370 1.6389 1.6534 4.9642 4.4857 0.8543 1.2003 1.1523 1.1632 1.6553 1.6954 5.0045 4.4493 0.9023 0.9385 1.2423 1.2045 1.6238 1.5625 5.4322 4.4830

表2 不同测试条件下联合加权系数的比较 Table 2 Comparison of joint weighted coefficients under different conditions

由表2可以看出, 人为篡改(裁剪替换)相比于一般的图像处理和噪声干扰所造成的图像失真, 其联合加权系数 φ明显偏高。因此实验表明:该方法对于人为篡改操作有很好的敏感性, 同时对于一般的图像处理和噪声干扰又有很好的鲁棒性, 因此对于区分两者的差异有着很好的效果。为了更全面地说明本文算法对于噪声干扰的鲁棒性, 引入人为篡改区分参数M, 其定义如下:

M=MtamperMchange(8)

式中:M_change为图像被改变的区域的大小; M_tamper为图像被人为篡改的区域大小, 其定义如下:

Mchange∈(Wsub≥η1)Mtamper∈Wsubmin(Woriginal, Wextracted)≥η2(9)

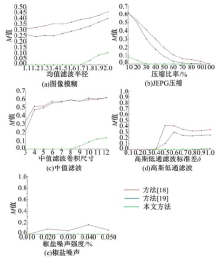
式中:W_sub为差分图像的像素值; W_original为原始水印图像的像素值; W_extracted为原始水印图像的像素值; η ₁, η ₂ 为设定的阈值比较参数, η ₁=0.05, η ₂=5, 为此, 本文准备了200幅512× 512大小的不同种类的图片与其他算法^{[18, 19]}相比转, 其M值的比较结果如图6所示。

由图6可见, 对于各种非恶意篡改的情况, 本文方法所得的 M值要显著低于其他方法, 说明本文方法能够有效抵抗各种非人为的图像改变, 因此, 本文方法在处理噪声干扰的情况下有着更高的鲁棒性。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 人为篡改区分参数M值对比Fig.6 Comparision of artificial distinguishes parameter M under different conditions

提出了一种具有高鲁棒性的图像数字水印算法, 在水印嵌入过程中, 利用视觉注意模型和最大熵原理生成原图像的显著图, 经过NMF降维和混沌加密后, 利用DCT-SVD方法嵌入到原图像中, 从而使得数字水印含有了原图像本身的内容信息。在篡改检测过程中, 利用基于Lorenz曲线的差异算法分别计算了像素值和像素位置的差异化程度, 从而能够很好地区分人为篡改和噪声干扰。设计的算法较好地平衡了各方面的要求, 实验也证实了本文方法的有效性。