基于高斯分解的多尺度3D Otsu阈值分割算法

引用本文

肖明尧, 李雄飞. 基于高斯分解的多尺度3D Otsu阈值分割算法. 2017, 47(1): 255-261
XIAO Ming-yao, LI Xiong-fei. Multi-scale 3D Otsu thresholding algorithm based on Gaussian decomposition. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 255-261 复制到剪切板

Permissions

基于高斯分解的多尺度3D Otsu阈值分割算法

肖明尧^1,², 李雄飞²

1.长春师范大学计算机科学与技术学院,长春 130032

2.吉林大学计算机科学与技术学院, 长春 130012

通讯作者:李雄飞(1963-),男,教授,博士生导师.研究方向:信息融合与数据挖掘.E-mail:lxf@jlu.edu.cn

作者简介:肖明尧(1980-),男,博士研究生.研究方向:数据挖掘与图像处理.E-mail:fengyuanqing@tom.com

基金:国家自然科学基金项目(61272209); 国家科技支撑计划项目(2012BAH48F02).

摘要

针对阈值图像分割算法对噪音敏感的问题,提出了一种新的基于分解的Otsu阈值分割算法。整个分割算法为一个迭代过程,在每次迭代中,该图像首先用3D Otsu算法进行分割,然后利用高斯核函数对原图像进行滤波,得到一个平滑的图像,然后被输入到下一个迭代中。最后,合并每次迭代过程中产生的分割结果,获得最终的分割结果。该算法的优点在于分割结果稳定,且具有较强的抗噪性。本文在MR大脑图像上进行实验,结果表明,该算法优于其他同类阈值分割算法。

关键词: 计算机应用; 图像分割; Otsu算法; 噪音; 高斯分解

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2017)01-0255-07

Multi-scale 3D Otsu thresholding algorithm based on Gaussian decomposition

XIAO Ming-yao^1,², LI Xiong-fei²

1.College of Computer Science and Technology, Changchun Normal University, Changchun 130032, China

2.College of Computer Science and Technology, Jilin University, Changchun 130012, China

Abstract

Current thresholding algorithms for image segmentation are sensitive to noise. To overcome this problem, a new Otsu thresholding algorithm is proposed based on image decomposition. The whole segmentation algorithm is designed as an iteration procedure. In each iteration the image is segmented by the 3D Ostu, and then it is filtered by Gaussian kernel filtering to get a smoothed image, which is taken as the input of the next iteration. Finally, segmentation results obtained in the iterations and are pooled to get final segmentation. The advantages of the proposed algorithm are that its segmentation results are stable and it is robust to noise. Experiments on medical MR brain images are conducted to demonstrate the effectiveness of the proposed method. Results indicate that the proposed algorithm is superior to other thresholding algorithms.

Keyword: computer application; image segmentation; Otsu algorithm; noises; Gaussian decomposition

Show Figures

0 引言

图像分割是指根据固有的特性(如灰度、质地、颜色和对比度等)将一个图像分割成若干非重叠的对象的技术^{[1, 2]}。目前, 图像分割技术已广泛应用于灰色/彩色自然图像^{[3, 4, 5]}、地形图^[6]、卫星图像^{[7, 8]}、和医疗图像等各种图像中^{[9, 10, 11]}。

现有分割算法可分为4类:①阈值分割类^{[12, 13, 14]}; ②聚类算法类^[15]; ③水平集类^[16]; ④图割类^[17]。其中, 基于直方图的阈值分割算法因其实现简单、效率较高的特点使用最为广泛。最经典的图像阈值分割算法包括最大类间方差(Otsu)方法^[18]、最小误差法^[19]和最大熵法^[20]。2012年, Lin等^[21]提出了一种新的基于Tsallis熵和局部长程关联的阈值图像分割算法。Cai等^[22]提出了一种基于Otsu的迭代三级阈值分割技术。Chang等^[23]提出了一种基于三维重建和降维技术的自适应3D最小误差阈值算法。这些阈值算法如何扩展到多阈值是一项重要且极具挑战性的工作^[7], 因为时间复杂度会随着阈值的数量呈指数增长^[24]。

多年来, 出现了许多改进的阈值技术来解决效率问题。Sarkar等^[3]提出了一种最小交叉熵(Minimum cross entropy, MCE)的算法, 可高效分离对象和背景。该方法利用差分进化(Differential evolution, DE)提高计算效率和鲁棒性。Bhandari等^[7]提出了使用杜鹃搜索(Cuckoo search, CS)的多阈值分割算法。Manikandan等^[12]使用遗传算法寻找最优阈值集。文献^[13]提出了一种自适应细菌觅食(Adaptive bacterial foraging, ABF)算法用于脑部MRI分割, 其采用自适应步长提高了传统细菌觅食(Bacterial foraging, BF)算法的搜索能力。Hammouche等^[25]提出了一种遗传算法与小波变换相结合的自动多阈值方法。该方法能够自动确定阈值的最佳数量以及最优阈值。

在过去几年中, 尽管图像分割技术得到了一定的发展, 但阈值分割技术仍然存在一些挑战, 如对噪音的鲁棒性较差^[26]。为了降低阈值分割算法的敏感性, 本文提出了一种新的多尺度3D Otsu分割算法。整个分割算法为一个迭代过程。在每次迭代中, 该图像首先被3D Otsu进行分割, 然后利用高斯核函数对原图像进行滤波, 得到一个平滑的图像, 并被输入到下一个迭代中。最后, 合并每个迭代过程产生的分割结果, 从而获得最终的分割结果。引入多尺度技术的目的在于, 通过平滑处理可不断去除噪声, 从而避免分割结果出现孤立点(洞)。同时, 考虑到平滑也会带来边缘的模糊, 造成边缘位置处像素分割错误。所以, 将各迭代过程中产生的分割结果进行合并, 可保证在去除噪音的同时避免边缘区域的分割错误。

1 分割算法

1.1 图像滤波

图像常被强度随机信号(也称为噪音)干扰。常见的噪音包括椒盐(Salt & Pepper)噪音、脉冲噪音、高斯噪音等。而噪音对于图像处理往往产生负面影响。因此, 对图像进行滤波以去除图像中的噪音则成为图像处理过程中重要的预处理步骤。

本文在滤波过程中, 选用高斯滤波器。原因在于高斯滤波器对去除正态分布的噪音有很好的效果, 同时对其他噪音的去除效果也有一定的效果。高斯滤波器是根据高斯函数的形状来选择权值的线性平滑滤波器。一维零均值高斯函数为 $\begin{matrix} g (x) = \exp [- x^{2} / (2 σ^{2})] 。 \end{matrix}$ 其中, $\begin{matrix} σ \end{matrix}$ 决定了高斯滤波器的宽度。对图像来说, 常用的二维零均值高斯函数定义为:

$\begin{matrix} g (x, y) = \exp [- (i^{2} - j^{2}) / (2 σ^{2})] \end{matrix}$ (1)

高斯滤波可看作是原图像与高斯函数的卷积运算, 对于源图像 $\begin{matrix} I, \end{matrix}$ 其高斯平滑结果为:

$\begin{matrix} \bar{I} = I ° g \end{matrix}$ (2)

式中:“ ° ” 为卷积操作算子。

1.2 三维Otsu

Otsu是一种经典的图像阈值分割算法。三维Otsu算法不仅考虑了像素的灰度信息, 而且考虑到了像素的空间信息, 包括邻近均值和邻域中值。所以, 三维Otsu具有一定的抗噪性能, 其分割效果优于一维Otsu和二维Otsu算法。

给出一幅灰度图像I, 大小为M× N, 灰度级为L。f(i, j)表示图像I中第i行第j列像素的灰度值。g(i, j)和h(i, j)分别表示W× W邻域内该像素的邻域均值和邻域中值, 定义如下所示:

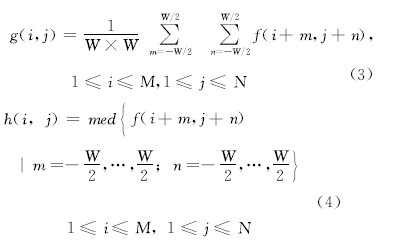
从式(3)和式(4)可以看出, g(i, j)和h(i, j)的取值范围均为0~L-1.

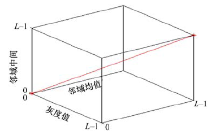
如图1所示, 三维Otsu直方图中的x, y, z坐标轴分别由f, g和h构成。直方图中的任意一点(x, y, z)表示图像I中的一个像素。设n_xyz表示三元组(x, y, z)出现的次数, p_xyz=n_xyz/(M× N) 表示(x, y, z)出现的概率, 且M× N= $\begin{matrix} \overset{L - 1}{\sum_{x = 0}} \end{matrix} \begin{matrix} \overset{L - 1}{\sum_{y = 0}} \end{matrix} \begin{matrix} \overset{L - 1}{\sum_{z = 0}} \end{matrix}$ n_xyz, $\begin{matrix} \overset{L - 1}{\sum_{x = 0}} \end{matrix} \begin{matrix} \overset{L - 1}{\sum_{y = 0}} \end{matrix} \begin{matrix} \overset{L - 1}{\sum_{z = 0}} \end{matrix}$ p_xyz=1。

	Figure Option View Download New Window
	图1 三维Otsu空间Fig.1 3D Otsu space

假定图像I被阈值三元组(r, s, t)分割为两个区域:背景区域C₀和目标区域C₁, 它们分别表示为C_0={(x, y, z)|0≤ x≤ r, 0≤ y≤ s, 0≤ z≤ t}和C₁={(x, y, z)|r+1≤ x≤ L-1, s+1≤ y≤ L-1, t+1≤ z≤ L-1}。如下所示:

$ω_{0} = \overset{r}{\sum_{x = 0}} \overset{s}{\sum_{y = 0}} \overset{t}{\sum_{z = 0}} p_{xyz}$ (5)

$ω_{1} = \overset{L - 1}{\sum_{x = r + 1}} \overset{L - 1}{\sum_{y = s + 1}} \overset{L - 1}{\sum_{z = t + 1}} p_{xyz}$ (6)

这两个区域的均值分别为:

$μ_{0} = [\begin{matrix} μ_{0}^{x} \\ μ_{0}^{y} \\ μ_{0}^{z} \end{matrix}] = [\begin{matrix} \overset{r}{\sum_{x = 0}} \overset{s}{\sum_{y = 0}} \overset{t}{\sum_{z = 0}} \frac{x P_{xyz}}{ω_{0}} \\ \overset{r}{\sum_{x = 0}} \overset{s}{\sum_{y = 0}} \overset{t}{\sum_{z = 0}} \frac{y P_{xyz}}{ω_{0}} \\ \overset{r}{\sum_{x = 0}} \overset{s}{\sum_{y = 0}} \overset{t}{\sum_{z = 0}} \frac{z P_{xyz}}{ω_{0}} \end{matrix}]$ (7)

$μ_{1} = [\begin{matrix} μ_{1}^{x} \\ μ_{1}^{y} \\ μ_{1}^{z} \end{matrix}] = [\begin{matrix} \overset{L - 1}{\sum_{x = r + 1}} \overset{L - 1}{\sum_{y = s + 1}} \overset{L - 1}{\sum_{z = t + 1}} \frac{x P_{xyz}}{ω_{1}} \\ \overset{L - 1}{\sum_{x = r + 1}} \overset{L - 1}{\sum_{y = s + 1}} \overset{L - 1}{\sum_{z = t + 1}} \frac{y P_{xyz}}{ω_{1}} \\ \overset{L - 1}{\sum_{x = r + 1}} \overset{L - 1}{\sum_{y = s + 1}} \overset{L - 1}{\sum_{z = t + 1}} \frac{z P_{xyz}}{ω_{1}} \end{matrix}]$ (8)

图像 $\begin{matrix} I \end{matrix}$ 的三维类间方差定义为

$σ_{B} (r, s, t) = ω_{0} [(μ_{0} - μ_{T}) {(μ_{0} - μ_{T})}^{T}] + ω_{1} [(μ_{1} - μ_{T}) {(μ_{1} - μ_{T})}^{T}]$ (9)

式中:μ _T 表示图像I的总均值, 即:

$\begin{matrix} μ_{T} = [\begin{matrix} μ_{T}^{x} \\ μ_{T}^{y} \\ μ_{T}^{z} \end{matrix}] = [\begin{matrix} \overset{L - 1}{\sum_{x = 0}} \overset{L - 1}{\sum_{y = 0}} \overset{L - 1}{\sum_{z = 0}} x P_{xyz} \\ \overset{L - 1}{\sum_{x = 0}} \overset{L - 1}{\sum_{y = 0}} \overset{L - 1}{\sum_{z = 0}} y P_{xyz} \\ \overset{L - 1}{\sum_{x = 0}} \overset{L - 1}{\sum_{y = 0}} \overset{L - 1}{\sum_{z = 0}} z P_{xyz} \end{matrix}] \end{matrix}$ (10)

三维Otsu阈值分割算法的目标是通过最大化矩阵 $\begin{matrix} σ_{B} \end{matrix}$ 的迹获得最优阈值三元组 $\begin{matrix} (r^{*}, s^{*}, t^{*}), \end{matrix}$ 即

$\begin{matrix} (r^{*}, s^{*}, t^{*}) = \underset{0 \leq r, s, t \leq L - 1}{argmax} {Tr (σ_{B} (r, s, t))} \end{matrix}$ (11)

三维Otsu阈值分割算法中, 阈值通过式(11)动态确定, 即不同的图像会得到不同的阈值。

1.3 分割结果整合

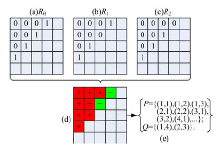
假设分解尺度为scale, 则分割结果可表示为 $\begin{matrix} {R_{0}, R_{1}, \dots, R_{scale}} 。 \end{matrix}$ 对于大多数的像素, 其在各个分割结果内的类标签是一致的。本文将其纳入到集合P中, 即 $= {p | p = \underset{p}{\arg} {R_{0} (p) = R_{1} (p) = \dots = R_{scale} (p)}}$ , 同时, 将其他像素归入到Q中。图2给出了一个示例, 说明如何确定集合P和Q。

图2(a)(b)(c)分别表示三个分割结果。图2(d)为通过判断各个像素在图2(a), 图2(b)和图2(c)是否相同得到的分类图谱, 其中内含“ +” 的红色单元表示对应的像素在各个分割结果中所属区域一致; 内含“ -” 的绿色单元对应的像素在各个分割结果中所属区域存在不一致。图2(e)为获得的集合P和Q。

	Figure Option View Download New Window
	图2 像素分类示例Fig.2 Illustration of pixel classification

对于像素 $\begin{matrix} p \in P, \end{matrix}$ 其最终的分割结果为:

$\begin{matrix} R (p) = R_{0} (p) \end{matrix}$ (12)

根据R(p)可以计算出每个类别的均值, 即{m₁, …, m_K}。

对于像素 $\begin{matrix} q \in Q, \end{matrix}$ 其最终的分割结果为:

$R (q) = R_{\hat{i}} (q)$ (13)

其中：

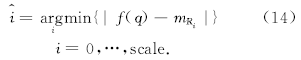
式中:f(q)表示像素q在原图像中的灰度值。

从式(12)(13)中可知, 集合 $\begin{matrix} Q \end{matrix}$ 内的像素的最终分割结果决定于其灰度值距离各个类别均值的差别。整合式(12)(13), 得到:

$\begin{matrix} R (p) = \{\begin{matrix} R_{0} (p), p \in P \\ R_{\hat{i}} (p), p \in Q \end{matrix} \end{matrix}$ (15)

1.4 算法框架

令 $\begin{matrix} I \end{matrix}$ 表示待分割的源图像。如图3所示, 该分割算法的整体流程可总结如下:

	Figure Option View Download New Window
	图3 本文分割算法框架Fig.3 Framework of the proposed segmentation algorithm

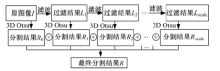
Step 1 利用3D Otsu阈值分割算法对原图像 $\begin{matrix} I \end{matrix}$ 进行分割(具体步骤见1.2节), 分割结果为 $\begin{matrix} R_{0} 。 \end{matrix}$

Step 2 利用高斯核函数对原图像 $\begin{matrix} I \end{matrix}$ 进行滤波, 得到平滑图像 $\begin{matrix} L_{1}; \end{matrix}$ 利用3D Otsu阈值分割算法对平滑图像L₁ 进行分割, 其结果保存为R₁ 。迭代运行Step 2, 在第 $\begin{matrix} {(i + 1)}_{t h} \end{matrix}$ 次迭代过程中, L_i首先进行滤波, 之后运行3D Otsu阈值分割算法得到分割结果 $\begin{matrix} R_{i + 1} 。 \end{matrix}$

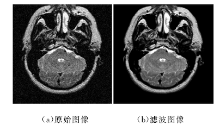
Step 3 迭代过程结束后, 利用式(15)将所有的分割结果 $\begin{matrix} {R_{0}, R_{1}, R_{2}, \dots, R_{scale}} \end{matrix}$ 进行整合, 以获得最终的分割结果R。

图4给出了高斯滤波的一个示例。可以发现, 经过滤波之后, 源图像中含有的噪音有了明显的减少。

	Figure Option View Download New Window
	图4 高斯滤波示例Fig.4 Illustration of Gaussian Filtering

2 实验结果及分析

2.1 实验设置

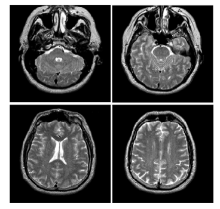
为了验证本文所提出的图像分割算法的性能, 与其他几种现有的图像分割算法进行了比较。参与比较的分割算法包括:1D Otsu和3D Otsu。测试图像来自哈佛大学脑部图像数据集(http://www.med.harvard.edu/aanlib/home.html)。测试图像包含4组, 如图5所示。

	Figure Option View Download New Window
	图5 本实验测试图像Fig.5 Test images in experiment

本实验中, 为了客观比较各分割算法的性能, 使用均一测度指标(uniformity)评估各分割结果^{[15, 17]}。均一测度指标定义为:

$\begin{matrix} u = 1 - 2 (K - 1) \frac{\overset{K}{\sum_{j = 1}} \sum_{i \in R_{j}} (f_{i} - μ_{j})^{2}}{Num (f_{\max} - f_{\min})} \end{matrix}$ (16)

式中:K表示分割的类别数; Num表示分割图像内包含像素的数量; f_max 、f_min 分别表示在原图像中的最大灰度值和最小灰度值; R_j表示第j个分割区域; f_i为像素i的灰度值; μ _j表示区域R_j的均值。均一测度指标的取值范围为[0, 1]。其中, u取值越大, 表明分割效果越好。

2.2 分割结果比较

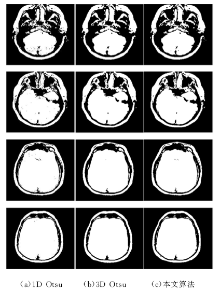
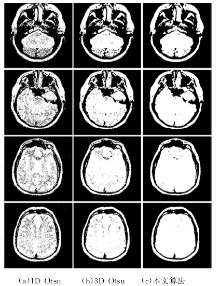
为了验证本文算法的有效性, 在Matlab R2009b环境下, 将1D Otsu、3D Otsu和本文方法进行实验对比, 实验中采用的测试图像如图5所示, 测试图像的尺寸均为256像素× 256像素, 灰度级为256。图6为三种分割算法的分割结果。

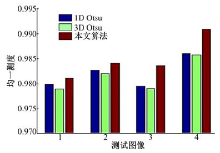
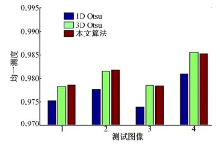
	Figure Option View Download New Window
	图6 各分割算法在测试图像上的分割结果Fig.6 Segmentations of test images by segmentation algorithms

图7从定量的角度分析了上面的4组试验, 这里采用的定量指标为均一测度, 该指标越大, 说明分割的精度越高, 分割效果越好。该图验证了本文算法较前两种方法更有效。

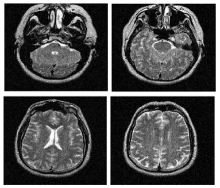
	Figure Option View Download New Window
	图7 图6中各分割图像的客观评价结果Fig.7 Objective evaluation of the segmented images in Fig.6

在实际应用中, 医学图像中经常或多或少地存在一些噪音。因此, 有必要检测本文算法对噪音的敏感性。本实验在图5所示的4幅测试图像中加入高斯白噪音(均值为0, 标准差为0.01), 分别得到4幅噪音图像, 如图8所示。利用噪音图像比较本文算法与其他两种算法对噪音的敏感性。

	Figure Option View Download New Window
	图8 含噪音的测试图像Fig.8 Noised test images

在噪音测试图像上, 1D Otsu, 3D Otsu以及本文算法得到的分割图像如图9所示。从图中可发现,

	Figure Option View Download New Window
	图9 噪音测试图像的分割结果Fig.9 Segmentation results of noised test images

1D Otsu得到的分割结果受到噪音的严重影响, 尤其是在软组织区域。相较于1D Otsu, 3D Otsu算法较好, 该算法因考虑了空间信息, 所以能够降低噪音对分割结果的影响。而本文算法得到的分割结果对噪音的鲁棒性更强, 从图像可以看出在软组织区域没有出现分割错误。

所有测试图像的最小灰度值均为0, 最大灰度值均为255。各个算法在噪音测试图像中的客观评价结果如图10所示。均一测度显示:本文算法整体上优于其他两个算法。

	Figure Option View Download New Window
	图10 图9中个分割图像的客观评价结果Fig.10 Objective evaluation result of the segmented images in Fig.9

3 结束语

针对图像分割中对噪音敏感的问题, 本文提出了一种新的基于高斯分解的阈值分割算法。该算法首先对图像进行高斯分解; 然后对图像的每个频段进行3D Otsu分割, 得到多个分割结果; 最后设计了一个分割结果的融合规则, 可将多个分割结果进行有效合并从而获得最终的分割结果。该算法在MR脑部图像上进行实验, 结果表明该方法能够有效降低噪声敏感度。经分析, 其原因在于本算法引入了高斯图像分解, 能够获得无噪声的图像频带, 保障最终的分割结果免受噪音的影响。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Zhang L, Ji Q. A Bayesian network model for automatic and interactive image segmentation[J]. IEEE Transactions on Image Processing, 2011, 20(9): 2582-2593. [本文引用:1]
[2]	Tlig L, Sayadi M, Fnaiech F. A new fuzzy segmentation approach based on S-FCM type 2 using LBP-GCO features[J]. Signal Processing: Image Communication, 2012, 27(6): 694-708. [本文引用:1]
[3]	Sarkar S, Das S, Chaudhuri S S. A multilevel color image thresholding scheme based on minimum cross entropy and differential evolution[J]. Pattern Recognition Letters, 2015, 54: 27-35. [本文引用:2]
[4]	Gómez D, Yáñez J, Guada C, et al. Fuzzy image segmentation based upon hierarchical clustering[J]. Knowledge-Based Systems, 2015, 87(c): 26-37. [本文引用:1]
[5]	景晓军, 李剑峰, 刘郁林. 一种基于三维最大类间方差的图像分割算法[J]. 自动化学报, 2003, 31(9): 1281-1285. Jing Xiao-jun, Li Jian-feng, Liu Yu-lin. Image segmentation based on 3-D maximum between-cluster variance[J]. Acta Electronica Sinica, 2013, 31(9) : 1281-1285. [本文引用:1]
[6]	Miao Q, Xu P, Liu T, et al. A novel fast image segmentation algorithm for large topographic maps[J]. Neurocomputing, 2015, 168: 808-822. [本文引用:1]
[7]	Bhand ari A K, Kumar A, Singh G K. Tsallis entropy based multilevel thresholding for colored satellite image segmentation using evolutionary algorithms[J]. Expert Systems with Applications, 2015, 42(22): 8707-8730. [本文引用:3]
[8]	Bhand ari A K, Kumar A, Singh G K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur's, Otsu and Tsallis functions[J]. Expert Systems with Applications, 2015, 42(3): 1573-1601. [本文引用:1]
[9]	Li C, Wang X, Eberl S, et al. Supervised variational model with statistical inference and its application in medical image segmentation[J]. IEEE Transactions on Biomedical Engineering, 2015, 62(1): 196-207. [本文引用:1]
[10]	Smistad E, Falch T L, Bozorgi M, et al. Medical image segmentation on GPUs—a comprehensive review[J]. Medical Image Analysis, 2015, 20: 1-18. [本文引用:1]
[11]	Aja-Fernández S, Curiale A H, Vegas-Sánchez-Ferrero G. A local fuzzy thresholding methodology for multiregion image segmentation[J]. Knowledge-Based Systems, 2015, 83: 1-12. [本文引用:1]
[12]	Manikand an S, Ramar K, Iruthayarajan M W, et al. Multilevel thresholding for segmentation of medical brain images using real coded genetic algorithm[J]. Measurement, 2014, 47: 558-568. [本文引用:2]
[13]	Sathya P D, Kayalvizhi R. Optimal segmentation of brain MRI based on adaptive bacterial foraging algorithm[J]. Neurocomputing, 2011, 74(14) : 2299-2313. [本文引用:2]
[14]	Maitra M, Chatterjee A. A novel technique for multilevel optimal magnetic resonance brain image thresholding using bacterial foraging[J]. Measurement , 2008, 41(10): 1124-1134. [本文引用:1]
[15]	罗述谦, 唐宇. 基于有偏场的适配模糊聚类分割算法[J]. 中国图象图形学报, 2002, 7(2): 111-114. Luo Shu-qian, Tang Yu. A bias based adaptive fuzzy segmentation algorithm[J]. Journal of Image and Graphics, 2002, 7(2): 111-114. [本文引用:2]
[16]	Li C, Huang R, Ding Z, et al. A level set method for image segmentation in the presence of intensity in homogeneities with application to MRI[J]. IEEE Transactions on Image Processing, 2011, 20(7): 2007-2016. [本文引用:1]
[17]	Dai S, Lu K, Dong J, et al. A novel approach of lung segmentation on chest CT images using graph cuts[J]. Neurocomputing, 2015, 168: 799-807. [本文引用:2]
[18]	Otsu N. A threshold selection method from gray-level histograms[J]. IEEE Transactions on Systems Man & Cybernetics, 2007, 9(1): 62-66. [本文引用:1]
[19]	Kittler J, Illingworth J. Minimum error thresholding[J]. Pattern Recognition, 1986, 19(1): 41-47. [本文引用:1]
[20]	Kapur J N, Sahoo P K, Wong A K C. A new method for gray-level picture thresholding using the entropy of the histogram[J]. Computer Vision, Graphics, and Image Processing, 1985, 29(3): 273-285. [本文引用:1]
[21]	Lin Q, Ou C. Tsallis entropy and the long-range correlation in image thresholding[J]. Signal Processing, 2012, 92(12): 2931-2939. [本文引用:1]
[22]	Cai H, Yang Z, Cao X, et al. , A new iterative triclass thresholding technique in image segmentation[J]. IEEE Transactions on Image Processing, 2014, 23(3): 1038-1046. [本文引用:1]
[23]	龙建武, 申铉京, 陈海鹏. 自适应最小误差阈值分割算法[J]. 自动化学报, 2012, 38(7) : 1134-1144. Long Jian-wu, Shen Xuan-jing, Chen Hai-peng. Adaptive minimum error thresholding algorithm[J]. Acta Automatica Sinica, 2012, 38(7) : 1134-1144. [本文引用:1]
[24]	Dey S, Saha I, Bhattacharyya S, et al. Multi-level thresholding using quantum inspired meta-heuristics[J]. Knowledge Based Systems, 2014, 67: 373-400. [本文引用:1]
[25]	Hammouche K, Diaf M, Siarry P. A multilevel automatic thresholding method based on a genetic algorithm for a fast image segmentation[J]. Computer Vision & Image Understand ing, 2008, 109(2): 163-175. [本文引用:1]
[26]	Chen X, Udupa J K, Bagci U, et al. Medical image segmentation by combining graph cuts and oriented active appearance models[J]. IEEE Transactions on Image Processing, 2012, 21(4): 2035-2046. [本文引用:1]

2011

0.0

... 0 引言图像分割是指根据固有的特性(如灰度、质地、颜色和对比度等)将一个图像分割成若干非重叠的对象的技术^[1,2] ...

2012

0.0

... 0 引言图像分割是指根据固有的特性(如灰度、质地、颜色和对比度等)将一个图像分割成若干非重叠的对象的技术^[1,2] ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

... Sarkar等^[3]提出了一种最小交叉熵(Minimum cross entropy, MCE)的算法,可高效分离对象和背景 ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

2003

0.0

. 2003, 31(9):1281-1285 DOI:doi:10.3321/j.issn:0372-2112.2003.09.001

Image segmentation based on 3-D maximum between-cluster variance

一种基于三维最大类间方差的图像分割算法

Jing Xiao-jun , Li Jian-feng , Liu Yu-lin.

景晓军, 李剑峰, 刘郁林

本文提出了一种基于三维最大类间方差的图像分割算法.该方法不仅利用了图像像元点的灰度分布信息,而且充分考虑了像元点之间的灰度相关信息,构造出三维观测空间,根据各信息间的竞争性、冗余性和互补性,进行有效的融合,得到比(一维)最大类间方差法更真实、准确的处理效果.理论分析和实验表明,对于低对比度、低信噪比的目标,该方法具有良好的分割性能.在该算法的基础上,又提出了一种快速递推三维最大类间方差法,减少了计算量,节约存储空间,具有较强的实用价值.

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

... 这些阈值算法如何扩展到多阈值是一项重要且极具挑战性的工作^[7],因为时间复杂度会随着阈值的数量呈指数增长^[24] ...

... Bhandari等^[7]提出了使用杜鹃搜索(Cuckoo search,CS)的多阈值分割算法 ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

2015

0.0

... 目前,图像分割技术已广泛应用于灰色/彩色自然图像^[3,4,5]、地形图^[6]、卫星图像^[7,8]、和医疗图像等各种图像中^[9,10,11] ...

2014

0.0

... 现有分割算法可分为4类:①阈值分割类^[12,13,14] ...

... Manikandan等^[12]使用遗传算法寻找最优阈值集 ...

2011

0.0

... 现有分割算法可分为4类:①阈值分割类^[12,13,14] ...

... 文献^[13]提出了一种自适应细菌觅食(Adaptive bacterial foraging,ABF)算法用于脑部MRI分割,其采用自适应步长提高了传统细菌觅食(Bacterial foraging, BF)算法的搜索能力 ...

2008

0.0

... 现有分割算法可分为4类:①阈值分割类^[12,13,14] ...

2002

0.0

. 2002, 7(2):111-114 DOI:doi:10.3969/j.issn.1006-8961.2002.02.002

A bias based adaptive fuzzy segmentation algorithm

基于有偏场的适配模糊聚类分割算法

Luo Shu-qian , Tang Yu.

罗述谦, 唐宇

近年来提出了许多监督和非监督模式识别技术用于磁共振图象的组织分类和定量分析。但是，这些方法的精度受到图象灰度不均匀性的严重影响。对于那些受灰度不均匀性影响的图象，如磁共振图象（MRI），提出了一种新的基于有偏场适配模糊聚类算法（BAFCM）来产生它们的分割结果。该算法通过修改C－means模糊算法中的目标方程，引入了描述灰度不均匀性的增益场，通过将增益场经为有偏场的计算，避免了AFCM中为保证增益场平滑缓慢变化引入的第一阶和第二阶正则项空间改变的二阶差分方程的复杂计算。其不仅对图象的灰度不均匀性进行了校正，而且实现了脑组织图象的快速全自动分割。

... ②聚类算法类^[15] ...

... 本实验中,为了客观比较各分割算法的性能,使用均一测度指标(uniformity)评估各分割结果^[15,17] ...

2011

0.0

... ③水平集类^[16] ...

2015

0.0

... ④图割类^[17] ...

... 本实验中,为了客观比较各分割算法的性能,使用均一测度指标(uniformity)评估各分割结果^[15,17] ...

2007

0.0

... 最经典的图像阈值分割算法包括最大类间方差(Otsu)方法^[18]、最小误差法^[19]和最大熵法^[20] ...

1986

0.0

... 最经典的图像阈值分割算法包括最大类间方差(Otsu)方法^[18]、最小误差法^[19]和最大熵法^[20] ...

1985

0.0

... 最经典的图像阈值分割算法包括最大类间方差(Otsu)方法^[18]、最小误差法^[19]和最大熵法^[20] ...

2012

0.0

... 2012年,Lin等^[21]提出了一种新的基于Tsallis熵和局部长程关联的阈值图像分割算法 ...

2014

0.0

... Cai等^[22]提出了一种基于Otsu的迭代三级阈值分割技术 ...

2012

0.0

. 2012, 38(7):1134-1144 DOI:doi:10.3724/sp.j.1004.2012.01134

Adaptive minimum error thresholding algorithm

自适应最小误差阈值分割算法

Long Jian-wu , Shen Xuan-jing , Chen Hai-peng.

龙建武, 申铉京, 陈海鹏

A robust minimum error thresholding method is proposed to combine the three-dimensional (3D) minimum error thresholding scheme based on 2D method with the principle of rebuilding and dimension reduction of the 3D histogram. Considering the global behavior of this approach and its ability to process even illumination images only, a water flow model is used to estimate the background of uneven illumination images for improving adaptability of the proposed method. Then, the difference image between the original image and background can be readily obtained to reduce the interference of uneven illumination during the binarization process. To improve execution performance of the segmentation procedure, gamma correction is employed to enhance image in addition to a global segmentation using robust minimum error thresholding algorithm. Subsequently, image segmentation tests are carried out with even and uneven illumination, and then comparison on misclassification error and time expenditure are performed between the proposed method and other approaches, i.e., 1D/2D minimum error thresholding, Otsu thresholding algorithm based on 3D histogram rebuilding and dimensionality reduction, adaptive gray wave transformation thresholding scheme, as well as a modified FCM method. The results show that the proposed approach yields better thresholding performance than those methods.

对二维最小误差法进行三维推广, 并结合三维直方图重建和降维思想提出了一种鲁棒的最小误差阈值分割算法. 但该方法为全局算法, 仅适用于分割均匀光照图像. 为提高其自适应性, 本文采用Water flow模型对非均匀光照图像进行背景估计, 以此获得原始图像与背景图像的差值图像, 达到降低非均匀光照对图像分割造成干扰的目的. 为进一步提高分割性能, 本文对差值图像采用γ 矫正进行增强, 然后采用鲁棒最小误差法进行全局分割, 从而完成目标提取. 最后本文对均匀光照下以及非均匀光照下图像进行了实验, 并与一维最小误差法、二维最小误差法、三维直方图重建和降维的Otsu阈值分割算法、灰度波动变换自适应阈值方法以及一种改进的FCM方法在错误分割率和运行时间上进行了对比. 实验结果表明, 相对于以上方法, 本算法的分割性能均有明显提升.

... Chang等^[23]提出了一种基于三维重建和降维技术的自适应3D最小误差阈值算法 ...

2014

0.0

... 这些阈值算法如何扩展到多阈值是一项重要且极具挑战性的工作^[7],因为时间复杂度会随着阈值的数量呈指数增长^[24] ...

2008

0.0

... Hammouche等^[25]提出了一种遗传算法与小波变换相结合的自动多阈值方法 ...

2012

0.0

... 在过去几年中,尽管图像分割技术得到了一定的发展,但阈值分割技术仍然存在一些挑战,如对噪音的鲁棒性较差^[26] ...