超声波的束射性和反射特性使利用声波主动测距成为可能, 超声波的频率越大, 指向性就越好, 但在空气中衰减越严重, 无法实现远距离探测^[12]。因此在设计超声波测距传感器时, 应选用较低的工作频率和较大的超声波换能器。对于共振频率为40 kHz, 辐射半径为6 mm的超声波探头, 有:

θ0=2arcsin0.61λaθ-3dB=2arcsin0.26λa(1)

式中:θ ₀ 、θ _-3dB分别为锐度角和波束角; λ 为超声波波长; a为换能器半径。

根据式(1)计算得锐度角 θ0≈120°,波束角 θ-3dB≈43°。实际应用中, 43° 的波束角仍然较大, 另外受到体积和发射功率的限制, 换能器半径无法进一步扩大。因此研究可使波束更加聚集的增强型超声波换能器显得尤为重要, 不仅能够减小超声波的波束角, 更能增强探测距离。

号筒作为增强声强的手段已经被广泛采用^[13], 按照图1建立增强型超声波发射声场仿真模型, 空气域是半径为100 mm, 角度为90° 的扇形区域, 设置环形区域为完美匹配层(PML), 使空气域的边界无反射, 从而形成无限大的声场, 号筒部分高h=28 mm, 窄口半径为7.1 mm, 宽口半径为 r。号筒内部为空气, 号筒壁为硬声场边界。采用频域研究方法, 设定研究频率为40 kHz。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 增强型超声波发射声场仿真模型Fig.1 Simulation model of enhanced ultrasonic transmitting sound field

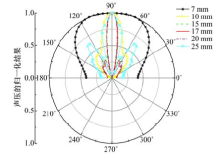
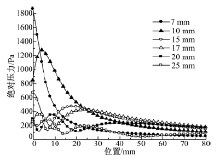
号筒优化的目的是使传感器辐射的声场在中心轴线上的能量更大, 而其余方向上的能量更小。宽口半径从7 mm变化到25 mm, 间隔1 mm。不同宽口大小的增强型超声波传感器的指向性和中心轴线上绝对声压比较如图2和图3所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 不同宽口大小号筒的指向性比较Fig.2 Directional comparison of different horns

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同宽口大小号筒的中心轴线声压比较Fig.3 Pressure comparison of different horns in central axis

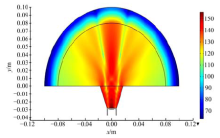
由图2和图3可知, 在号筒宽口半径为15~20 mm时, 超声波传感器的指向性较好, 其中心轴线上的绝对声压也是最高的。随着宽口半径缩小, 其指向性越差, 中心轴线上的绝对声压也越小; 随着宽口半径增大, 虽然在指向性上仍然具有较好的主瓣方向, 但旁瓣也随之增大, 导致其中心轴线上的绝对声压有所减小。则用h=28 mm, 窄口半径为7.1 mm, r=17 mm的锥形号筒为增强手段的超声波传感器发射声场分布如图4所示。图中的色条表示声压级, 单位为dB。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 增强型超声波传感器发射声场分布图Fig.4 Acoustic field distribution of enhanced transducer

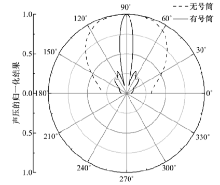
为了更加直观地区分出普通超声波传感器和增强型超声波传感器在性能上的优劣, 提取两80 cm处圆弧上的绝对压力, 并做归一化处理, 做出传感器的波束图, 如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 普通型与增强型传感器指向性比较Fig.5 Directional comparison of optimized transducer and normal transducer

另外提取中心轴线上的绝对压力, 对比出声压的增幅, 如图6所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 普通型与增强型传感器轴线声压比较Fig.6 Sound pressure comparison of optimized transducer and normal transducer in central axis

由图5可知, 有号筒的超声波传感器相比于无号筒的, 其指向性提升较为明显。由图6可知, 有号筒的超声波传感器中心轴线上的绝对声压比无号筒的大。取20~80 mm处两者的声压相除后取平均值, 则有号筒的传感器在中心轴线上辐射的声压比无号筒的大3.5倍。因此可以认为, 加上号筒的增强型超声波传感器的测距范围更大。

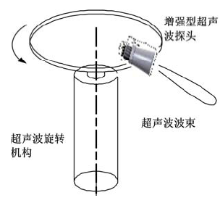
利用激光^[14]、无线电波^[15]的旋转扫描系统已经得到了广泛的应用, 但基于超声波的旋转扫描系统却很少在文献中出现。单发单收超声波周向扫描系统示意图如图7所示, 超声波探头使用加装号筒的增强型超声波传感器, 步进电机带动装有增强型超声波探头的平台进行旋转, 就可以对周围360° 范围内的目标进行探测。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 超声波周向扫描示意图Fig.7 Schematic diagram of ultrasonic circumferential scanning

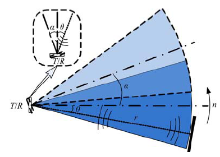
采用扫描方法会导致探测区域出现周期性的探测盲区, 这是周向扫描方案的固有缺陷。只有当扫描转速足够快, 才能有效地减小周期性探测盲区对探测性能的影响。然而当超声波测距传感器旋转扫描时, 发射超声波脉冲后, 测距传感器会旋转一定的角度, 导致接收回波变小, 测距范围也会相应地减小, 因此超声波周向扫描的转速受到一定的限制。超声波周向扫描接收回波示意图如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 超声波周向扫描接收回波示意图Fig.8 Schematic diagram of ultrasonic echo when rotational scanning

根据上文仿真分析结果和实验所得数据可知, 增强型超声波测距传感器在静止条件下最远探测距离是10 m, 如图9中的虚线所示。超声波周向扫描转速为 n(r/min), 当发射的超声波经距离为 r、方位角为 θ(定义与超声波传感器垂直方向为0° , 逆时针旋转为负, 顺时针旋转为正)的目标反射后到达传感器时, 超声波传感器已经旋转了 α, α=2rc×nπ30,其中c为超声波在空气中的传播速度, 取344 m/s。假设目标为全反射, 声压不发生衰减; 另外假设超声波为球面波辐射, 在空气中传播时只考虑扩散衰减, 因此声压随距离成反比衰减。那么超声波对距离为 r, 方位角为 θ的目标探测时的接收回波为:

Precv(r, θ)=Ptrans(θ)2r×cos(θ+α)(2)

式中: Ptrans(θ)为超声波传感器在 θ角方向上的声压, 将 α=2rc×nπ30带入式(2), 且只有当 Precv(r, θ)大于等于超声波传感器能感知的最小声压幅值时, 距离为 r、方位角为 θ的目标才能被探测到。

Ptrans(θ)2r×cos(θ+2rc×nπ30)≥Ptrans020(3)

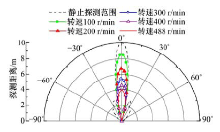
由式(3)可知, 根据不同的扫描速度, 每个方向上都对应一个最大探测距离, 由这些最大探测距离就可得出不同扫描速度下超声波测距传感器单次探测时的感知范围, 如图9所示。不同转速下单次探测的最远距离如图10所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 不同扫描速度下单次探测的测距范围Fig.9 Distance measuring range in different scanning speed

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 不同转速下0° 角最大探测距离Fig.10 Maximum range of 0° in different scanning speed

由图9可知, 随转速的升高, 超声波测距传感器的探测范围不断减小。并且当转速大于488 r/min时, 在0° 附近的角度的最大探测距离会出现负值, 主要原因是0° 附近的角度可测距离较大, 因此往返时间较多, 导致超声波传感器在高转速下旋转的角度过大, 回波无法出现在接收视场中。因此应根据实际应用中的监控范围选择合适的扫描速度, 由图10可知, 当监控范围为周边6 m区域时, 超声波周向扫描转速应低于253 r/min。

由超声波周向扫描探测系统工作过程可知, 在一个扫描周期内, 会形成多条超声波声束构成周向声束场。由于增强型超声波波束角较小, 因此将声束简化为一条直线, 则一个扫描周期内的超声波声束如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 一个扫描周期内的超声波声束Fig.11 Distribution of ultrasonic beam in one scanning period

为保证每个扫描周期中的超声波声束数量相同且在固定角度 η上, 在图11中, 相邻声束间的夹角之和为2π , 为保证每个扫描周期中的超声波声束数量相同且在固定角度上, 则超声波单次测距周期 T与机构扫描转速 n(r/min)之间应存在如下关系:

knπT30=2π(4)

式中: k∈Z,表示一个扫描周期内有 k个探测点; 由于超声波发射和接收处理时间远小于在空气中的传播时间, 因此周期 T=(2rmax)/c,其中 rmax为最大监控距离, c为超声波在空气中的传播速度。

设最大监控距离为6 m, 超声波在空气中传播速度为344 m/s, 那么根据上文的计算结果 n≤253r/min,在保证k为正整数的前提下, k为6、7、8、9、10时, n分别为286.67、245.71、215、191.11、172。可知, 当k< 7时, 转速 n已经超过了253 r/min, 因此保证一个扫描周期有固定探测点的最高转速为245.71 r/min, 但是此时探测点的数量为7条, 转速中有小数, 在实际应用过程中很难保证。因此本文选取转速215 r/min, 此时一个扫描周期内的超声波测距声束有8条, 每条声束之间的夹角为45° 。

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 超声波扫描车辆探测示意图Fig.12 Schematic diagram of detecting vehicle with ultrasonic rotational scanning

超声波周向扫描感知节点的车辆探测示意图如图12所示。超声波扫描机构旋转转速为 n(r/min), 车辆长为 l, 宽为b。假设车辆行驶轨迹为直线, 且超声波未垂直入射目标时(目标行驶轨迹与超声波波束不垂直, 但只偏转小角度), 并不影响其探测距离。由于超声波周向扫描探测具有周期性的探测盲区, 因此探测行驶中的车辆目标时, 有可能丢失目标。

车辆经过监控区域的路线较多, 但是最有可能丢失目标的情况是车辆行驶轨迹只通过一条超声波声束, 那么车辆通过监控区域的时间t=l/v。为了能够捕获到目标, 必须在这段时间内保证超声波扫描机构完成大于等于一个周期的扫描, 即 60/n≤t。对于超声波周向扫描, 具有最好波束分布的最大扫描转速n=215 r/min, 因此对于l=5 m长度的车辆目标, 超声波周向扫描能够捕获最大速度为64.5 km/h行驶的目标。如果增加超声波阵元, 形成多发多收的超声波周向扫描, 那么在同等转速下, 扫描一周的时间更短, 可用于监控更高速的目标; 或在较低的转速下, 形成更多的超声波波束, 使得角度分辨率提高, 用于监控较小的目标。

本文基于增强型超声波测距传感器设计了单发单收旋转扫描系统, 量化了号筒对超声波传感器的增强效果, 并仿真优化号筒的尺寸和外形。增强型超声波测距传感器在波束的指向性和声音能量的聚集等方面获得较大的提升, 因此可以获得更大的测距范围。基于增强型超声波的声场分布, 对单发单收旋转扫描系统的主要参数进行了优化, 并利用优化结果计算出该系统的目标捕获率。在最大扫描转速为215 r/min时, 能够捕获速度小于64.5 km/h的目标, 若要监控更高速度或更小体积的目标时, 只需在旋转机构上添加额外的阵元。本文对增强型超声波周向旋转扫描系统的研究为超声波测距技术在有向传感器网络目标监控领域的应用提供了参考。