基于特征空间MUSIC算法的相干信号波达方向空间平滑估计

引用本文

石要武, 陈淼, 单泽涛, 石屹然, 单泽彪. 基于特征空间MUSIC算法的相干信号波达方向空间平滑估计. 2017, 47(1): 268-273
SHI Yao-wu, CHEN Miao, SHAN Ze-tao, SHI Yi-ran, SHAN Ze-biao. Spatial smoothing technique for coherent signal DOA estimation based on eigen space MUSIC algorithm. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 268-273 复制到剪切板

Permissions

基于特征空间MUSIC算法的相干信号波达方向空间平滑估计

石要武¹, 陈淼¹, 单泽涛², 石屹然¹, 单泽彪^1,³

1.吉林大学通信工程学院,长春 130022

2.诺博橡胶制品有限公司, 河北保定 072550

3.长春理工大学电子信息工程学院,长春 130022

作者简介:石要武(1954-),男,教授,博士生导师.研究方向:现代信号处理.E-mail:shiyw@jlu.edu.cn

基金:国家自然科学基金项目(61571462); 吉林省青年科研基金项目(20140520064JH).

摘要

为了高效、准确地估计相干信号的波达方向(DOA),提出了一种基于特征空间多重信号分类(MUSIC)算法的空间平滑估计方法。首先对相干信号进行空间平滑处理,然后对其应用特征空间MUSIC算法进行DOA的精确估计,使其最大限度地利用信号子空间和噪声子空间的信息。本文方法并不影响非相关信号存在时DOA的估计,且还可以对信号源功率进行有效的估计,以提高对小能量信号的成功估计概率。与传统空间平滑算法及修正MUSIC算法相比,本文方法具有更低的信噪比门限和更高的估计精度及分辨力。最后的仿真实验验证了本文方法的有效性和鲁棒性。

关键词: 信息处理技术; 波达方向估计; 相干信号; 特征空间; 空间平滑技术; 信号源功率估计

中图分类号:TN911 文献标志码:A 文章编号:1671-5497(2017)01-0268-06

Spatial smoothing technique for coherent signal DOA estimation based on eigen space MUSIC algorithm

SHI Yao-wu¹, CHEN Miao¹, SHAN Ze-tao², SHI Yi-ran¹, SHAN Ze-biao^1,³

1.College of Communication Engineering, Jilin University, Changchun 130022, China

2.Nuobo Rubber Production Co., Ltd., Baoding 072550,China

3.School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130022, China

Abstract

To estimate the Direction of Arrival (DOA) of coherent signals accurately and quickly, a new decorrelation method based on spatial smoothing technique and eigen space multiple signal classification (MUSIC) is presented. After spatial smoothing of the coherent signals, the eigen space MUSIC algorithm is applied to estimate the DOA in order to make maximal use of the information of signal and noise subspaces. In addition, the DOA estimation of uncorrelated signals is not affected, as well as the power of signal sources can be estimated effectively, which can improve the probability of success in the estimation of low power signals. The proposed method possesses a better resolving ability and a lower SHR threshold than conventional spatial smoothing technique and modified MUSIC algorithm for DOA estimation of coherent signals. The simulation results demonstrate that the proposed method is effective and robust in DOA estimation.

Keyword: information processing; direction of arrival(DOA) estimation; coherent signal; eigen space; spatial smoothing technique; signal source power estimation

Show Figures

0 引言

由于传播环境的复杂性, 入射到实际阵列中的强相关或相干源信号是普遍存在的。而且对于强相关或相干源信号, 传统的波达方向(Direction of arrival, DOA)估计算法, 如经典的MUSIC(Multiple signal classification)算法、ESPRIT(Estimation of signal parameters via rotational invariance techniques)算法和最小范数法等特征分解类算法^[1], 已经无法有效地进行DOA估计, 因此, 研究有效的解相干算法是当前阵列信号处理领域中一个重要的研究方向^{[2, 3]}。

常见的解相干方法有最大似然方法、Toeplitz矩阵重构及空间平滑类预处理方法等。最大似然方法^[4]是通过概率密度模型来进行相干源信号处理的, 具有较好的解相干效果, 但是它最终需要非线性多维搜索来实现DOA估计, 计算量巨大。Toeplitz矩阵重构类算法^[5]的最大优点是没有阵列孔径的损失, 但它在矩阵重构过程中没有充分考虑到信号的先验信息, 所以在信号源功率不相同的场合其估计精度会相对变差。空间平滑类方法(Spatial smoothing techniques, SST)最早是由Evans等^[6]提出, 随后经Shan等^[7]改进了的一种常用且有效的解相干预处理方法。这种解相干方法是以牺牲阵列的有效孔径为代价的, 为了减少阵列孔径的损失, Pillai等^[8]在前人研究的基础上提出了一种双向空间平滑算法, 即前后向空间平滑算法。随后, 很多学者对其进行了拓展和改进^{[9, 10]}, 其中, Kundo^[11]结合经典MUSIC算法提出了一种修正MUSIC(Modified MUSIC, MMUSIC)算法用于解相干处理。MMUSIC算法的最大优点是没有阵列孔径的损失, 但是, 该算法实质是前后向空间平滑算法中取子阵列个数为1时的特殊情况, 所以它仅能对两个相干源信号进行有效的解相干处理。Zhang等^[12]在传统MUSIC算法的基础上提出了一种特征空间MUSIC(Eigen space MUSIC, ES-MUSIC)算法, 该算法得到的谱峰更加尖锐, 旁瓣更低, 而且可以估计信号源的功率。同时, 在对ES-MUSIC算法进行修正后可以进一步估计相干信号源的DOA, 并取得了不错的解相干效果。但是其仍然无法对超过两个的相干信号源进行DOA估计, 且无法对相干信号的功率进行准确地估计。

针对上述问题, 本文将空间平滑技术与ES-MUSIC算法相结合, 提出了一种基于ES-MUSIC的空间平滑估计(SS-ESMUSIC)方法。该方法首先对相干源信号进行空间平滑技术解相干处理, 然后, 对其应用ES-MUSIC算法进行精确的DOA估计, 使其最大限度地利用信号子空间和噪声子空间的信息。本文方法突破了MMUSIC算法和特征空间MMUSIC(ES-MMUSIC)算法中相干信号源数目仅为两个的限制, 并且可以对相干源信号的功率进行有效地估计。最后将本文方法与MMUSIC和ES-MMUSIC算法进行了仿真对比实验, 结果证明了本文方法的有效性及优越性。

1 阵列信号数学模型

假设有 $\begin{matrix} K \end{matrix}$ 个远场窄带目标信号源, 其DOA分别为 $\begin{matrix} θ_{1}, θ_{2}, \dots, θ_{K} 。 \end{matrix}$ 由 $\begin{matrix} M \end{matrix}$ 个各向同性阵元构成的等间距直线阵, 各阵元位置分别为 $\begin{matrix} 0, d_{1}, \dots, d_{M - 1}, \end{matrix}$ 且 $\begin{matrix} M > K, \end{matrix}$ 则第 $\begin{matrix} m \end{matrix}$ 个阵元的输出为:

$\begin{matrix} x_{m} (t) = \overset{K}{\sum_{k = 1}} s_{k} (t) \exp (- j \frac{2 π}{λ} d_{m - 1} \sin θ_{k}) + g_{m} (t) \end{matrix}$ (1)

式中: $\begin{matrix} s_{k} (t) \end{matrix}$ 表示接收到的第 $\begin{matrix} k \end{matrix}$ 个源信号; $\begin{matrix} θ_{k} \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 个源信号的DOA; $\begin{matrix} g_{m} (t) \end{matrix}$ 表示该阵元上方差为 $\begin{matrix} σ^{2} \end{matrix}$ 的高斯白噪声; $\begin{matrix} λ \end{matrix}$ 为信号波长。定义 $\begin{matrix} θ_{k} \end{matrix}$ 的方向向量为:

$\begin{matrix} \begin{matrix} a (θ_{k}) = [1, \exp (- j \frac{2 π}{λ} d_{1} \sin θ_{k}), \dots, \\ {\exp (- j \frac{2 π}{λ} d_{M - 1} \sin θ_{k})]}^{T} \end{matrix} \end{matrix}$ (2)

则阵列输出信号可写成如下矩阵形式:

$X (t) = AS (t) + G (t)$ (3)

式中：

$\begin{matrix} X (t) & = {[x_{1} (t), x_{2} (t), \dots, x_{M} (t)]}^{T}; \\ A & = [a (θ_{1}), a (θ_{2}), \dots, a (θ_{K})]; \\ S (t) & = {[s_{1} (t), s_{2} (t), \dots, s_{K} (t)]}^{T}; \\ G (t) & = {[g_{1} (t), g_{2} (t), \dots, g_{M} (t)]}^{T} 。 \end{matrix}$

根据式(3)可得阵列输出信号协方差矩阵为:

$\begin{matrix} R = E [X (t) X^{H} (t)] = A R_{S} A^{H} + σ^{2} I_{M} \end{matrix}$ (4)

式中: $\begin{matrix} R_{S} = E [S (t) S^{H} (t)] \end{matrix}$ 为信号协方差矩阵; $\begin{matrix} I_{M} \end{matrix}$ 为 $\begin{matrix} M \end{matrix}$ 阶单位阵。

在实际环境中相干信号源是普遍存在的, 所谓相干信号, 其实质是它们之间只相差一个复常数。假设存在 $\begin{matrix} K \end{matrix}$ 个相干信号源, 则有:

$\begin{matrix} \begin{matrix} s_{k} (t) = α_{k} s_{0} (t) \\ k = 1, 2, \dots, K \end{matrix} \end{matrix}$ (5)

式中: $\begin{matrix} s_{0} (t) \end{matrix}$ 称为生成信源; $\begin{matrix} α_{k} \end{matrix}$ 表示为第 $\begin{matrix} k \end{matrix}$ 个信号源 $\begin{matrix} s_{k} (t) \end{matrix}$ 相对于生成信源的复增益。将式(5)带入式(3)得到相干信号的数学模型为:

$\begin{matrix} \begin{matrix} X (t) = AS (t) + G (t) = \\ A {[α_{1} s_{0} (t), α_{2} s_{0} (t), \dots, α_{K} s_{0} (t)]}^{T} + G (t) = \\ Aη s_{0} (t) + G (t) \end{matrix} \end{matrix}$ (6)

式中: $\begin{matrix} η = {[α_{1}, α_{2}, \dots, α_{K}]}^{T} 。 \end{matrix}$

2 本文方法

2.1 空间平滑技术

空间平滑技术是处理强相关或相干信号的有效方法, 其基本思想是将具有相同子阵列流型的均匀线阵分成若干个相互重叠的子阵列, 然后再将各子阵列的协方差矩阵相加平均后以取代原来意义上的协方差矩阵, 从而解决了矩阵的秩亏损问题^{[7, 8]}, 即将协方差矩阵的秩恢复到等于信号源的个数。

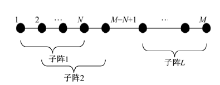
如图1所示, 有一个由 $\begin{matrix} M \end{matrix}$ 个阵元构成的线列阵, 利用前向滑动方式划分为 $\begin{matrix} L \end{matrix}$ 个子阵列, 其中每个子阵列有 $\begin{matrix} N \end{matrix}$ 个阵元, 即 $\begin{matrix} N = M - L + 1 。 \end{matrix}$ 取最左边子阵列为参考阵列, 则第 $\begin{matrix} l \end{matrix}$ 个前向子阵列的输出为:

$\begin{matrix} \begin{matrix} {X^{f}}_{l} (t) = {[x_{l} (t), x_{l + 1} (t), \dots, x_{l + N - 1} (t)]}^{T} = \\ A_{N} D^{l - 1} S (t) + G_{l} (t) \end{matrix} \end{matrix}$ (7)

式中: $\begin{matrix} A_{N} = [a_{N} (θ_{1}), a_{N} (θ_{2}), \dots, a_{N} (θ_{K})] \end{matrix}$ 为参考阵列的流型矩阵; $\begin{matrix} D = diag [\exp (j \frac{2 πd}{λ} \sin θ_{1}), \exp (j \frac{2 πd}{λ} \sin θ_{2}), \dots, \exp (j \frac{2 πd}{λ} \sin θ_{K})] 。 \end{matrix}$ 因此, 可得到该子阵列数据协方差矩阵为:

$\begin{matrix} \begin{matrix} {R^{f}}_{l} = E [{X^{f}}_{l} (t) ({X^{f}}_{l} {(t))}^{H}] = \\ A_{N} D^{l - 1} R_{S} (D^{l - 1})^{H} {A^{H}}_{N} + σ^{2} I_{N} \end{matrix} \end{matrix}$ (8)

式中: $\begin{matrix} I_{N} \end{matrix}$ 表示 $\begin{matrix} N \end{matrix}$ 阶单位阵。

	Figure Option View Download New Window
	图1 前向空间平滑示意图Fig.1 Forward spatial smoothing scheme

前向空间平滑技术是通过求取各前向子阵列的协方差矩阵的均值来实现秩恢复的, 即前向空间平滑协方差矩阵为:

$\begin{matrix} R^{f} = \frac{1}{L} \overset{L}{\sum_{l = 1}} {R^{f}}_{l} = A_{N} {R^{f}}_{S} {A^{H}}_{N} + σ^{2} I_{N} \end{matrix}$ (9)

式中: $\begin{matrix} {R^{f}}_{S} = \frac{1}{L} \overset{L}{\sum_{l = 1}} D^{l - 1} R_{S} (D^{l - 1})^{H} 。 \end{matrix}$

同理, 可得后向空间平滑协方差矩阵为:

$\begin{matrix} R^{b} = \frac{1}{L} \overset{L}{\sum_{l = 1}} {R^{b}}_{L - l + 1} = A_{N} {R^{b}}_{S} {A^{H}}_{N} + σ^{2} I_{N} \end{matrix}$ (10)

式中: $\begin{matrix} {R^{b}}_{S} = \frac{1}{L} \overset{L}{\sum_{l = 1}} D^{N + l - 2} R_{S} D^{2 - N - l} \end{matrix}$ 。

前向空间平滑协方差矩阵 $\begin{matrix} R^{f} \end{matrix}$ 和后向空间平滑协方差矩阵 $\begin{matrix} R^{b} \end{matrix}$ 实质上互为共轭倒序阵, 利用共轭倒序不变性, 可得前后向空间平滑协方差矩阵为:

$\begin{matrix} R^{fb} = (R^{f} + R^{b}) / 2 \end{matrix}$ (11)

2.2 特征空间MUSIC算法

对式(11)进行特征分解, 得到:

$\begin{matrix} R^{fb} = U_{S} Σ_{S} {U^{H}}_{S} + U_{G} Σ_{G} {U^{H}}_{G} \end{matrix}$ (12)

式中: $\begin{matrix} Σ_{S} \end{matrix}$ 和 $\begin{matrix} Σ_{G} \end{matrix}$ 分别为较大特征值和较小特征值所构成的对角阵; $\begin{matrix} U_{S} \end{matrix}$ 和 $\begin{matrix} U_{G} \end{matrix}$ 分别为较大特征值和较小特征值对应的特征向量所构成的信号子空间与噪声子空间。由于空间噪声为高斯白噪声, 所以有:

$\begin{matrix} Σ_{G} = σ^{2} I_{N - K} \end{matrix}$ (13)

式中: $\begin{matrix} I_{N - K} \end{matrix}$ 为 $\begin{matrix} N - K \end{matrix}$ 阶单位阵。通过式(13)可估计得到噪声方差为:

$\begin{matrix} σ^{2} = \frac{1}{N - K} tr (Σ_{G}) \end{matrix}$ (14)

式中: $\begin{matrix} tr (\cdot) \end{matrix}$ 表示求迹运算。

理想条件下, 信号子空间与噪声子空间是相互正交的, 阵列流型中的方向向量同样正交于噪声子空间, 即:

$\begin{matrix} {a^{H}}_{N} (θ) U_{G} = 0 \end{matrix}$ (15)

另外, 根据信号源功率的计算过程, 定义矩阵:

$\begin{matrix} \begin{matrix} R_{A} = A_{N} R_{S}^{fb} {A^{H}}_{N} = A_{N} \frac{{R^{f}}_{S} + {R^{b}}_{S}}{2} {A^{H}}_{N} = \\ A_{N} P {A^{H}}_{N} = U_{S} (Σ_{S} - σ^{2} I_{K}) {U^{H}}_{S} \end{matrix} \end{matrix}$ (16)

式中: $\begin{matrix} I_{K} \end{matrix}$ 为 $\begin{matrix} K \end{matrix}$ 阶单位阵。单取第 $\begin{matrix} k \end{matrix}$ 个信号的方向向量, 进一步计算可得:

$\begin{matrix} \begin{matrix} {a^{H}}_{N} (θ_{k}) R_{A}^{+} a_{N} (θ_{k}) = \\ a^{H} (θ_{k}) (A_{N} P {A^{H}}_{N})^{+} a_{N} (θ_{k}) = \\ {[A_{N}^{+} a_{N} (θ_{k})]}^{H} P^{+} A_{N}^{+} a_{N} (θ_{k}) = \\ {δ^{T}}_{k} P^{+} δ_{k} = [P^{+}]_{kk} = 1 / p_{k} \end{matrix} \end{matrix}$ (17)

式中: $\begin{matrix} {(\cdot)}^{+} \end{matrix}$ 表示求伪逆运算; $\begin{matrix} δ_{k} = {[0, \dots, 1, 0, \dots, 0]}^{T} \end{matrix}$ 为 $\begin{matrix} N \end{matrix}$ 维向量; $\begin{matrix} p_{k} \end{matrix}$ 为第 $\begin{matrix} k \end{matrix}$ 个信源的功率。因此, 得到一种新的空间谱函数:

$\begin{matrix} P_{ES - MUSIC} (θ) = \frac{{a^{H}}_{N} (θ) R_{A}^{+} a_{N} (θ)}{{a^{H}}_{N} (θ) U_{G} {U^{H}}_{G} a_{N} (θ)} \end{matrix}$ (18)

对上述空间谱函数进行搜索, 当 $\begin{matrix} θ = θ_{k} (k = 1, 2, \dots, K) \end{matrix}$ 时, $\begin{matrix} {a^{H}}_{N} (θ_{k}) U_{G} {U^{H}}_{G} a_{N} (θ_{k}) = 0, \end{matrix}$ 而 $\begin{matrix} {a^{H}}_{N} (θ_{k}) R_{A}^{+} a_{N} (θ_{k}) = 1 / p_{k}, \end{matrix}$ 则空间谱函数 $\begin{matrix} P_{ES - MUSIC} (θ) \end{matrix}$ 在 $\begin{matrix} θ_{k} \end{matrix}$ 处出现谱峰。所以, 可以利用谱函数 $\begin{matrix} P_{ES - MUSIC} (θ) \end{matrix}$ 进行DOA估计。式(18)空间谱函数的定义实质是利用信号源功率的倒数对其空间谱进行加权, 以实现抑制噪声的目的。所以, 式(18)不仅可以实现DOA的估计, 还可以利用式(17)进行信号源功率的估计, 便于对小能量信号的检测判断。

2.3 算法步骤

(1)估计前后向空间平滑协方差矩阵 $\begin{matrix} R^{fb} 。 \end{matrix}$

(2)对协方差矩阵 $\begin{matrix} R^{fb} \end{matrix}$ 进行特征值分解: $\begin{matrix} R^{fb} = U_{S} Σ_{S} {U^{H}}_{S} + U_{G} Σ_{G} {U^{H}}_{G}, \end{matrix}$ 并估计噪声方差 $\begin{matrix} σ^{2} 。 \end{matrix}$

(3)根据 $\begin{matrix} R_{A} = U_{S} (Σ_{S} - σ^{2} I_{K}) {U^{H}}_{S}, \end{matrix}$ 计算 $\begin{matrix} R_{A}^{+} = U_{S} (Σ_{S} - σ^{2} I_{K})^{- 1} {U^{H}}_{S} 。 \end{matrix}$

(4)使 $\begin{matrix} θ \end{matrix}$ 变化, 按照 $\begin{matrix} P_{ES - MUSIC} (θ) = \frac{{a^{H}}_{N} (θ) R_{A}^{+} a_{N} (θ)}{{a^{H}}_{N} (θ) U_{G} {U^{H}}_{G} a_{N} (θ)} \end{matrix}$ 来计算谱函数, 通过谱峰搜索得到DOA的估计值。

(5)对估计出DOA的信号进行功率估计: $\begin{matrix} p_{k} = 1 / [{a^{H}}_{N} (θ_{k}) R_{A}^{+} a_{N} (θ_{k})] (k = 1, 2, \dots, K) 。 \end{matrix}$

3 实验验证及比较

3.1 DOA估计的性能对比

实验1 与传统空间平滑估计方法的性能对比。

实验中采用阵元间距为半波长、阵元数 $\begin{matrix} M = 8 \end{matrix}$ 的均匀线阵。并假设相干信号源数已知, 且其DOA分别为-50° 、-10° 和25° 。在快拍数为100、信噪比为0 dB时, 采用传统空间平滑SS-MUSIC方法和本文SS-ESMUSIC方法在利用空间平滑技术划分为3个子阵列时的空间谱如图2所示。从图2中可以看出, SS-MUSIC方法和SS-ESMUSIC方法均可以在DOA方向形成明显的谱峰, 但是, 与SS-MUSIC方法相比, SS-ESMUSIC方法的谱峰更加尖锐, 峰值更高, DOA估计性能更优越。同时, 针对上述两种方法在不同子阵划分情况下分别进行了1000次Monte Carlo DOA估计实验。并给出了如表1中所示的DOA估计均方根误差:

$\begin{matrix} RMS E_{θ} = \sqrt[]{\frac{1}{KQ} \overset{K}{\sum_{k = 1}} \overset{Q}{\sum_{q = 1}} {[{\hat{θ}}_{k} (q) - θ_{k}]}^{2}} \end{matrix}$ (19)

式中: $\begin{matrix} Q \end{matrix}$ 为实验总次数; $\begin{matrix} {\hat{θ}}_{k} (q) \end{matrix}$ 为第 $\begin{matrix} q \end{matrix}$ 次Monte Carlo实验DOA真实值 $\begin{matrix} θ_{k} \end{matrix}$ 的估计值。

	Figure Option View Download New Window
	图2 两种空间平滑方法的空间角谱图Fig.2 Spatial angular spectrum of two spatial smoothing methods

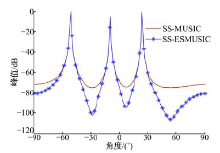
从表1中可以得知, 在相同子阵个数划分情况下, SS-ESMUSIC方法的估计性能均优于SS-MUSIC方法, 这主要是因为本文方法利用了功率倒数对其空间谱进行加权, 最大限度地利用了噪声子空间和信号子空间两者的信息, 对噪声具有较强的抑制能力, 而SS-MUSIC方法仅利用了噪声子空间。另外从表1中还可以看出, 针对同一种方法, 其均方根误差随着子阵个数的增加而有所增大, 这是由于子阵个数的增加进一步降低了阵列的有效孔径所致。

表1 不同子阵划分下的均方根误差 Table 1 Root mean square error of DOA estimation versus number of subarrays

方法	子阵个数
方法	$\begin{matrix} L = 3 \end{matrix}$	$\begin{matrix} L = 4 \end{matrix}$	$\begin{matrix} L = 5 \end{matrix}$
SS-MUSIC	0.8457	0.9803	1.2178
SS-ESMUSIC	0.8386	0.9783	1.2033

表1 不同子阵划分下的均方根误差 Table 1 Root mean square error of DOA estimation versus number of subarrays

实验2 与其他解相干算法的性能对比。

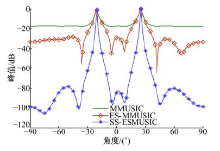
选取两种具有代表性的相干信号DOA估计算法:MMUSIC^[11]和ES-MMUSIC^[12]算法, 与本文方法进行比较。由于MMUSIC和ES-MMUSIC算法仅能对两个相干信号源进行DOA估计, 故采用两个相干信号源进行仿真实验。其DOA分别为-20° 和25° , 子阵数L=3, 其他条件同实验1。从图3中可以看出, 相同条件下, SS-ESMUSIC方法要优于另外两种解相干算法, 主要表现为其谱宽更窄、峰值更大、主峰更加尖锐, 并且旁瓣相对更低, 说明本文方法具有更好的鲁棒性。

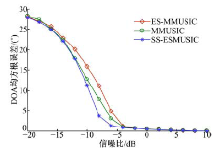
	Figure Option View Download New Window
	图3 不同解相干算法的空间角谱图Fig.3 Spatial angular spectrum of different decorrelation methods

为了进一步验证本文SS-ESMUSIC方法的有效性和优越性, 在不同信噪比条件下, 对上述3种算法分别进行了1000次Monte Carlo实验, 比较上述3种方法的DOA估计成功概率(定义为正确估计DOA(偏差小于或等于2° )次数的比例)和以式(19)计算的均方根误差。

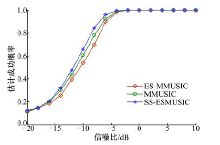
从图4不同信噪比估计成功概率的曲线中可以看出, 当信噪比高于-5 dB时, 3种方法的估计成功概率基本相当, 都接近于1。而随着信噪比的不断下降, SS-ESMUSIC方法的估计成功概率明显要高于另外两种算法, 说明本文方法具有更低的信噪比门限以及更好的分辨能力。

	Figure Option View Download New Window
	图4 DOA估计成功概率Fig.4 Success probability of DOA estimation

图5给出了上述3种方法在不同信噪比时的DOA估计均方根误差。由图5可知, 上述3种方法的均方根误差随着信噪比的不断增大均在减小, 当信噪比达到-5 dB左右时, 3种方法DOA估计的均方根误差大致相同。但是, 在信噪比小于-5 dB时, 另外两种算法的DOA估计均方根误差要大于本文SS-ESMUSIC方法, 说明本文方法在较低信噪比条件下, 具有更高的估计精度及更好的稳健性。

	Figure Option View Download New Window
	图5 DOA估计均方根误差Fig.5 Root mean square error of DOA estimation

实验3 不同解相干算法的分辨力对比。

考虑在阵元数 $\begin{matrix} M = 8 、 \end{matrix}$ 信噪比为5 dB且快拍数为500的情况下, 假设存在2个相干信号源, 应用MMUSIC算法、ES-MMUSIC算法和本文SS-ESMUSIC方法对该相干信号源在不同DOA间距下, 分别进行了1000次Monte Carlo DOA估计实验。表2给出了上述3种方法在不同DOA间隔条件下的估计成功概率(估计偏差小于或等于2° 时次数的比例)。从表2中可以看出, 随着信源DOA间隔的增大, 3种方法的估计成功概率均增大, 但是在相同DOA间隔条件下, 本文方法均具有最高的估计成功概率, 说明本文方法比另外两种算法具有更高的分辨力。

表2 DOA估计成功分辨概率 Table 2 Resolution probability of DOA estimation

3.2 信号源功率估计

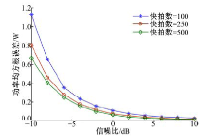
假设有如同3.1节实验1中的3个相干信号源, 其信号功率分别为1.0、0.9和0.8 W。在不同信噪比情况下, 对其进行了1000次独立的Monte Carlo功率估计实验。图6给出了不同快拍数(100, 250, 500)情况下, 以式(20)计算的功率估计均方根误差随信噪比变化的曲线。

$\begin{matrix} RMS E_{p} = \sqrt[]{\frac{1}{KQ} \overset{K}{\sum_{k = 1}} \overset{Q}{\sum_{q = 1}} {[{\hat{p}}_{k} (q) - p_{k}]}^{2}} \end{matrix}$ (20)

式中: $\begin{matrix} {\hat{p}}_{k} (q) \end{matrix}$ 为第 $\begin{matrix} q \end{matrix}$ 次Monte Carlo实验信号功率 $\begin{matrix} p_{k} \end{matrix}$ 的估计值。

从图6中可以看出, 本文方法在小快拍数、低信噪比条件下仍具有较好的功率估计性能, 并且其均方根误差随着信噪比的增大或者快拍数的增加在逐渐减小。

	Figure Option View Download New Window
	图6 功率估计均方根误差Fig.6 Root mean square error of power estimation

4 结束语

提出了一种基于ES-MUSIC的空间平滑估计方法。首先, 利用空间平滑技术对相干源信号进行解相干预处理。然后, 对其应用ES-MUSIC算法进行DOA的精确估计, 使其充分利用信号与噪声两个子空间的信息。本文方法并不影响非相关信号存在时DOA的估计, 且还可以估计非相关或相干信号源的功率, 使其更加适用于小能量信号或低信噪比条件下的DOA估计。与修正MUSIC算法相比, 本文方法确实存在阵列孔径损失的问题, 但是仍具有比其他算法更高的估计精度及更强的分辨能力, 尤其所得谱峰更加尖锐、旁瓣更低、更加易于谱峰优化搜索。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王布宏, 王永良, 陈辉. 相干信源波达方向估计的加权空间平滑算法[J]. 通信学报, 2003, 24(4): 31-40. Wang Bu-hong, Wang Yong-liang, Chen Hui. Weighted spatial smoothing algorithm for direction of arrival estimation of coherent sources[J]. Journal on Communications, 2003, 24(4): 31-40. [本文引用:1]
[2]	Qian C, Huang L, Zeng W J, et al. Direction-of-arrival estimation for coherent signals without knowledge of source number[J]. IEEE Sensors Journal, 2014, 14(9): 3267-3273. [本文引用:1]
[3]	Tao H, Xin J M, Wand J S, et al. Two-dimensional direction estimation for a mixture of noncoherent and coherent signals[J]. IEEE Transactions on Signal Processing, 2014, 63(2): 318-333. [本文引用:1]
[4]	Stoica P, Arye N. Music, maximum likelihood, and cramer-rao bound[J]. IEEE Transactions on Acoustics Speech and Signal Procession, 1989, 373(5): 720-741. [本文引用:1]
[5]	Linebarger D A. Redundancy averaging with large arrays[J]. IEEE Transactions on Signal Processing, 1993, 41(4): 1707-1710. [本文引用:1]
[6]	Evans J E, Johnson J R, Sun D F. High resolution angular spectrum estimation techniques for terrain scattering analysis and angle of arrival estimation[C]//Processing 1st ASSP Workshop Spectral Estimation, Hamilton, Ontario Canada, 1981: 134-139. [本文引用:1]
[7]	Shan T J, Wax M, Lailath T. On spatial smoothing for estimation of coherent signals[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1985, 33(4): 806-811. [本文引用:2]
[8]	Pillai S U, Kwon B H. Forward/backward spatial smoothing techniques for coherent signal identification[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1989, 37(1): 8-15. [本文引用:2]
[9]	Todros K, Hero A O. Robust multiple signal classification via probability measure transformation[J]. IEEE Transactions on Signal Processing, 2015, 63(5): 1156-1170. [本文引用:1]
[10]	Zhang W, Liu W, Wang J, et al. Joint transmission and reception diversity smoothing for direction finding of coherent targets in MIMO radar[J]. IEEE Journal of Selected Topics in Signal Processing, 2014, 8(1): 115-124. [本文引用:1]
[11]	Kundu D. Modified MUSIC algorithm for estimating DOA of signals[J]. Signal Processing, 1996, 48(1): 85-90. [本文引用:2]
[12]	Zhang X F, Lü W, Shi Y, et al. A novel DOA estimation algorithm based on eigen space[C]//IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Hangzhou, China, 2007: 551-554. [本文引用:2]

2003

0.0

... 而且对于强相关或相干源信号,传统的波达方向(Direction of arrival,DOA)估计算法,如经典的MUSIC(Multiple signal classification)算法、ESPRIT(Estimation of signal parameters via rotational invariance techniques)算法和最小范数法等特征分解类算法^[1],已经无法有效地进行DOA估计,因此,研究有效的解相干算法是当前阵列信号处理领域中一个重要的研究方向^[2,3] ...

2014

0.0

2014

0.0

1989

0.0

... 最大似然方法^[4]是通过概率密度模型来进行相干源信号处理的,具有较好的解相干效果,但是它最终需要非线性多维搜索来实现DOA估计,计算量巨大 ...

1993

0.0

... Toeplitz矩阵重构类算法^[5]的最大优点是没有阵列孔径的损失,但它在矩阵重构过程中没有充分考虑到信号的先验信息,所以在信号源功率不相同的场合其估计精度会相对变差 ...

1981

0.0

... 空间平滑类方法(Spatial smoothing techniques,SST)最早是由Evans等^[6]提出,随后经Shan等^[7]改进了的一种常用且有效的解相干预处理方法 ...

1985

0.0

... 空间平滑类方法(Spatial smoothing techniques,SST)最早是由Evans等^[6]提出,随后经Shan等^[7]改进了的一种常用且有效的解相干预处理方法 ...

... 1 空间平滑技术空间平滑技术是处理强相关或相干信号的有效方法,其基本思想是将具有相同子阵列流型的均匀线阵分成若干个相互重叠的子阵列,然后再将各子阵列的协方差矩阵相加平均后以取代原来意义上的协方差矩阵,从而解决了矩阵的秩亏损问题^[7,8],即将协方差矩阵的秩恢复到等于信号源的个数 ...

1989

0.0

... 这种解相干方法是以牺牲阵列的有效孔径为代价的,为了减少阵列孔径的损失,Pillai等^[8]在前人研究的基础上提出了一种双向空间平滑算法,即前后向空间平滑算法 ...

2015

0.0

... 随后,很多学者对其进行了拓展和改进^[9,10],其中,Kundo^[11]结合经典MUSIC算法提出了一种修正MUSIC(Modified MUSIC,MMUSIC)算法用于解相干处理 ...

2014

0.0

... 随后,很多学者对其进行了拓展和改进^[9,10],其中,Kundo^[11]结合经典MUSIC算法提出了一种修正MUSIC(Modified MUSIC,MMUSIC)算法用于解相干处理 ...

1996

0.0

... 随后,很多学者对其进行了拓展和改进^[9,10],其中,Kundo^[11]结合经典MUSIC算法提出了一种修正MUSIC(Modified MUSIC,MMUSIC)算法用于解相干处理 ...

... 选取两种具有代表性的相干信号DOA估计算法:MMUSIC^[11]和ES-MMUSIC^[12]算法,与本文方法进行比较 ...

2007

0.0

... Zhang等^[12]在传统MUSIC算法的基础上提出了一种特征空间MUSIC(Eigen space MUSIC,ES-MUSIC)算法,该算法得到的谱峰更加尖锐,旁瓣更低,而且可以估计信号源的功率 ...

... 选取两种具有代表性的相干信号DOA估计算法:MMUSIC^[11]和ES-MMUSIC^[12]算法,与本文方法进行比较 ...