作者简介:管欣(1961-),男,教授,博士生导师.研究方向:汽车动态仿真与控制.E-mail:guan.hsin@ascl.jlu.edu.cn
为了减小视觉系统的传输延迟对汽车驾驶模拟器的影响,应用机动目标跟踪理论中的当前统计(CS)模型并结合自适应卡尔曼预测方法,对汽车驾驶模拟器中车辆的位置进行预测,形成针对驾驶模拟器视觉系统传输延迟的当前统计模型补偿器。建立了驾驶员-驾驶模拟器仿真模型,分析了传输延迟对驾驶行为的影响,对比了当前统计模型补偿器与美国国家先进驾驶模拟器(NADS)的补偿器、改进的McFarland补偿器的补偿效果,结果表明当前统计模型补偿器具有更好的补偿效果,并在ASCL开发型汽车驾驶模拟器上对该补偿器进行了验证。
In order to decrease the influence of transport delay on driving simulator, a compensator for vision system was built combining the Current Statistical (CS) model and Adaptive Kalman Predictor (AKP) to predict vehicle's position. A simulation model of the driver-driving simulator was proposed. The influence of transport delay on driving behavior was analyzed with this simulation model. Also a comparison between the compensator based on CS model and other two representative compensators, the National Advanced Driving Simulator and an improved McFarland compensator, was done with the proposed model. The results show that the compensator based on CS model has a better compensation effect. The effectiveness of this compensator was also verified on the ASCL driving simulator.
汽车驾驶模拟器是典型的人在回路仿真系统, 它能够模拟出驾驶真实车辆时的视景、操纵、声响、运动感觉, 由此可以模拟人-车-环境闭环系统的运动响应, 预测和验证闭环系统性能, 从而对汽车、交通环境进行设计改进[1]。
汽车驾驶模拟器的视觉系统传输延迟是指, 从视觉系统接收到来自车辆动力学计算机的表示车辆位置、姿态发生变化的数据到相应的变化情况显示到视景, 被驾驶员感知到的时间[2]。视觉系统传输延迟会导致驾驶员的驾驶感觉与真车不一致, 甚至还会出现驾驶不适, 这些都会严重影响驾驶模拟器在汽车主观评价、驾驶行为研究等领域的应用效果[2, 3, 4]。
传输延迟现象在飞行模拟器中也同样存在, 国内外为此提出了一些补偿方法, 获得了较好的补偿效果[5, 6, 7]。然而相比于飞机, 地面车辆的动力学响应更快、驾驶员的驾驶操作也更复杂, 这使得汽车驾驶模拟器的传输延迟补偿问题变得更加复杂[3]。而且目前在汽车驾驶模拟器的传输延迟补偿方面公开发表的文章还很少, 比如美国国家公路交通安全管理局(NHTSA)曾对其国家先进驾驶模拟器(NADS)各个子系统的传输延迟情况进行了分析, 并先后采用了数值积分方法和借鉴于飞行模拟器的McFarland方法对其视觉系统传输延迟进行补偿[2, 3, 8]。法国的Oktal公司对其SCANeR驾驶模拟器中各个系统的传输延迟进行了测量和分析, 并提出了一些减小传输延迟的方法, 然而对存在较大传输延迟的视觉系统却没有给出专门的补偿方法[4]。
传输延迟补偿的核心问题是对仿真对象未来一段时间内的运动状态进行预测。机动目标跟踪理论虽然起源于航空航天, 但在智能车辆行驶轨迹的预测等方面已经有了广泛的应用[9, 10]。
本文首先建立了驾驶员-驾驶模拟器仿真模型, 以便分析传输延迟对驾驶模拟器应用效果的影响, 验证延迟补偿算法的效果。然后建立了基于当前统计模型的传输延迟补偿器, 对驾驶模拟器的视觉系统传输延迟进行补偿, 仿真分析表明其效果优于NADS所使用的补偿器和飞行模拟器使用的改进的McFarland补偿器。驾驶模拟器试验结果表明, 本文提出的补偿器能够无缝嵌入到已有的模拟器系统中, 满足实时性要求, 并具有较好的补偿效果。
为了能够直观地分析传输延迟对驾驶模拟效果的影响, 高效地开发、对比分析各类传输延迟补偿方法的性能, 建立了包括驾驶员模型、车辆动力学模型、视觉系统模型的驾驶员-驾驶模拟器仿真模型, 如图1所示。驾驶员模型输出的方向盘、油门、制动踏板的控制量传递给车辆动力学模型, 车辆动力学模型的计算结果中有关位置变化的分量经过视觉系统模型反馈给驾驶员模型, 其他的车辆动力学模型计算结果直接反馈给驾驶员模型。
驾驶员的方向控制采用了基于圆弧式预瞄算法的预瞄跟随模型, 该模型能够模拟出驾驶员的神经和肌肉反应滞后, 对大曲率路径也具有很好的跟随效果[11]。驾驶员的纵向速度控制采用了分相PID控制模型, 其对目标速度变化比较剧烈的工况也具有很好的跟随效果[12]。结合上述两种控制方法, 可以对各类剧烈的实验工况实现较为理想的轨迹和速度跟随效果[13]。
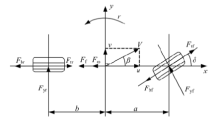
因为所使用的驾驶员模型仅需要对车辆的纵向、侧向和横摆进行控制, 所以为简化计算过程, 建立了仅包含纵向、侧向、横摆三个自由度的简单车辆动力学模型来代替驾驶模拟器中使用的复杂动力学模型。如图2所示, 得到车辆的三自由度模型计算公式(1)(2)(3):
式中:Ftf 、Fbf 为前轮所受的驱动力和制动力; Ftr、Fbr为后轮所受的驱动力和制动力; Fyf 、Fyr为前、后轮所受的轮胎侧向力; Ff 为滚动阻力; Fω 为空气阻力; u、v分别为车辆的纵、侧向速度; β 为质心侧偏角; δ 、r为前轮转角和车辆横摆角; a、b为质心到前、后轴的距离;
视觉系统根据车辆动力学模型的计算结果对驾驶员的视点位置进行更新, 并不存在动力学过程, 但是因为数据传输、融合处理、视景渲染过程中的缓存切换、投影显示刷新等过程使动力学模型计算结果的显示产生了滞后, 因此将其描述为一个纯滞后环节
当前统计模型(CS模型)由我国学者周宏仁[14]提出, 在机动目标跟踪领域有着广泛的应用。模型认为, 当目标以某一加速度机动时, 下一时刻的加速度取值是有限的, 且只能在“ 当前” 加速度的邻域内, 如果采用修正的瑞利分布来表征机动加速度的特性, 则加速度可以描述为式(4)(5)[14]:
式中:x(t)为目标位置; a(t)为零均值有色加速度噪声;
据此, 本文建立了基于当前统计模型的车辆某一自由度运动过程的离散状态方程和观测方程:
式中:
式中:T为采样时间间隔; 系统噪声W(k)是均值为0、方差为Q(k)的高斯白噪声序列; 观测噪声V(k)是均值为0、方差为R(k)的高斯白噪声序列, 且W(k)与V(k)不相关。
系统的噪声方差
式中:
根据式(6)(7)(12)可以得到如下的自适应卡尔曼滤波方程:
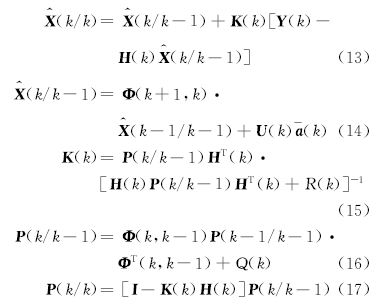
如果将
式中:
由此便可以得到对未来T时刻的预测。
驾驶员的视觉对车辆在横向、纵向、横摆3个自由度的变化十分敏感, 所以选择上述3个自由度进行传输延迟补偿, 将式(19)中的预测时长取为驾驶模拟器的传输延迟时间
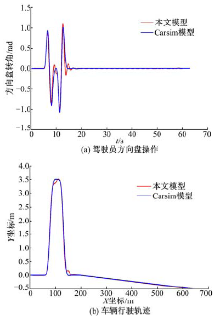
将所建立的驾驶员-驾驶模拟器仿真模型的视觉系统传输延迟时间设置为0, 与商业仿真软件Carsim中驾驶员-复杂动力学模型的标准工况仿真结果进行对比分析, 如图3所示。40 km/h双移线的仿真对比结果表明, 所建立的驾驶员-驾驶模拟器仿真模型的仿真结果与Carsim基本一致, 其仿真结果可以作为后续仿真分析的依据。
仿真分析了传输延迟时间对驾驶操纵行为的影响。图4为利用所建立的驾驶员-驾驶模拟器仿真模型进行的40 km/h双移线仿真试验结果, 仿真过程分别设置视觉系统传输延迟时间为无延迟、50 ms、75 ms和100 ms。
 | 图4 不同延迟时间双移线仿真的驾驶员操作和车辆轨迹Fig.4 Driver operation and vehicle trajectory for double lane change simulation with different transport delay time |
仿真结果表明, 传输延迟会导致驾驶员开始操作方向盘的时刻向后推移, 车辆行驶轨迹开始进入移线的位置也会随之向后推移; 同时传输延迟会导致驾驶员的方向盘操作发生不应有的振荡, 而且随着传输延迟时间的增加, 振荡现象愈加剧烈, 车辆的行驶轨迹也随之产生振荡, 这些振荡在真实的双移线试验中都不会出现。
在所建立的驾驶员-驾驶模拟器仿真模型中, 加入传输延迟补偿器模块(见图5), 该模块负责对车辆动力学模型输出的位置进行传输延迟补偿, 然后再传递给视觉系统模型。分别实现了美国国家先进驾驶模拟器(National advanced driving simulator, NADS)所使用的补偿器、文献[7]中应用于飞行模拟器的改进的McFarland补偿器以及本文提出的当前统计模型补偿器。
 | 图5 传输延迟补偿器与驾驶员-驾驶模拟器仿真模型Fig.5 Transport delay compensator and driver-driving simulator simulation model |
如图6所示, 给出了40 km/h双移线仿真结果, 应用以上3种补偿器分别对50 ms、75 ms和100 ms传输延迟时间进行了传输延迟补偿。
仿真对比结果表明, 3种补偿器对视觉系统的传输延迟都能够起到补偿作用。其中NADS补偿器随着传输延迟时间的增加, 其补偿效果会逐渐变差,
 | 图6 不同延迟时间下双移线仿真车辆轨迹Fig.6 Vehicle trajectory for double lane change simulation with different transport delay time |
图6(c)中
如图7所示, 在40 km/h蛇形工况下, 改进的McFarland补偿器采用与图6(c)中相同的补偿器参数对100 ms的传输延迟进行补偿时已经出现了计算发散的情况, 相比之下当前统计模型补偿器不但能够对100 ms的传输延迟进行补偿, 而且从
在吉林大学汽车仿真与控制国家重点实验室的ASCL开发型汽车驾驶模拟器上对当前统计模型补偿器的传输延迟补偿效果进行了试验验证。对比了驾驶模拟器在无传输延迟补偿器和使用当前统计模型补偿器两种情况下驾驶员的方向盘操作结果。试验路况选择在一段双向四车道的街区场景中进行, 试验过程中没有其他交通车辆干扰驾驶员的驾驶, 驾驶员需连续转弯通过交叉路口, 并要求驾驶员尽量保持在内侧车道行驶, 直线行驶时车速应不低于60 km/h, 转弯行驶时车速应不低于30 km/h。实验结果如图8所示。
对比试验结果可以发现, 在使用了当前统计模型补偿器的情况下, 驾驶员在入弯时打方向盘的时刻会提前, 在路口转弯处的方向盘操作幅度较小, 在出弯路进入直路后不会出现明显的剧烈振荡; 反之, 在无补偿器的情况下, 驾驶员在通过路口的过程中方向盘操作幅度较大, 且出弯路进入直路后方向盘仍会有明显的振荡过程。该试验虽然不能定量地分析传输延迟补偿器的补偿效果, 但仍然可以直观地看到使用了当前统计模型补偿器后, 对驾驶员的操作所起到的有益作用, 并且该补偿器的补偿效果也比较理想。
通过对驾驶员-驾驶模拟器仿真模型的仿真分析以及驾驶模拟器的驾驶试验可得到以下结论:①传输延迟会对驾驶模拟器的操作性能产生影响, 并且延迟时间越长, 对操作性能的影响越大; ②基于当前统计模型的驾驶模拟器传输延迟补偿器对不同程度的视觉系统传输延迟都具有很好的补偿效果, 并且不会受到驾驶工况的影响, 可以应用于驾驶模拟器中。今后, 还可以尝试利用当前统计模型补偿器对车辆动力学模型的加速度变化进行预测、跟踪, 从而将其应用在体感模拟系统的传输延迟补偿之上。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|