作者简介:崔林林(1986-),男,博士研究生.研究方向:声学定位,无线传感器网络.E-mail:cuilinlinxinxiang@126.com
针对当前基于TDOA(波达时间差)的空间交汇声定位算法中,在整个定位区域采用单一的定位算法的不足,提出了一种基于区域划分的声定位算法。在定位区域内布设4个六元阵,根据区域误差均值最小的原则,确定基阵的各个参数,并将该区域划分成16个子区域,每个子区域将采取不同的定位算法。以炮竹作为声源,在北京郊区的一块200 m×200 m的定位区域中随机选取3个声源点,每个点重复实验3次,每个点的定位误差均小于1 m。
At present, the space intersection acoustic localization algorithm based on Time Difference of Arrival (TDOA) only uses a simplex localization method. We herein propose an acoustic localization algorithm based on region division. In this algorithm, we set four spatial six-element arrays, confirm the array parameters based on the principle of minimizing the mean value of area errors, and then divide such area into 16 sub-regions, to each of which we apply different localization algorithm. With fireworks as the sound source, we randomly selected three sound source points in a plot in suburban of Beijing with area of 200 m × 200 m, and carried out repeated experiments for three times at each point. The localization errors at the three points are all less than 1 m.
常用的声定位算法分为三类:一是基于波束成型的方法; 二是基于高分辨率谱估计的方法; 三是基于波达时间差(TDOA)的方法。由于前两种方法存在计算量大且不利于实时计算等缺点, 近几年来基于TDOA的声定位方法得到了高度重视。基于TDOA的被动声定位技术[1, 2, 3]是通过测得声源到声传感器阵列的时延信息, 然后采用特定的定位算法进行解算, 进而得到声源在空间中的位置信息。目前, 国内外常用的声传感器阵列有四元阵、五元阵、六元阵以及圆形阵等。其中, 四元阵的缺点[4]是定向定距与方位角有关, 且定位精度差; 五元阵定位模型[5, 6, 7]能取得较好的定位效果, 但俯仰角对定距精度有较大影响; 六元阵[8]虽然消除了有效声速和阵形参数对定向估计精度的影响, 但是单个阵列对声源距离的估计精度尚没有达到实用水平。因此, 目前使用多个基阵交汇定位的算法比较流行。但是, 由于两个基阵中心连线附近区域的定位误差比其他区域的误差大, 而以往的交汇定位算法中[9], 定位区域没有被区别对待, 在整个定位区域内仅采用单一定位算法[10]。
针对上述不足, 本文提出了一种基于区域划分的空间交汇声定位算法, 实验结果证明该算法不仅可以有效地消除声速对声定位的影响, 而且可以有效地提高定位精度。
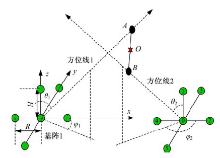
在定位区域内布设4个立体六元阵, 在进行声源定位时, 每个六元阵根据声源到达各个阵元的时间解算出一个空间角(即声源到六元阵中心点的俯仰角和方位角), 由空间角和基阵中心坐标值可以确定4条空间直线(称之为“ 方位线” ), 最终通过方位线的空间交汇原理解算声源的初始坐标。由于误差的存在, 两条方位线在空间中不会交汇于一点, 可先确定两条方位线的公垂线, 再取公垂线的中点作为声源的初始解算点。然后, 根据区域划分算法, 进行二次解算, 最终得到声源坐标的修正值。
图1为两个六元阵的交汇示意图, A点和B点的连线为基阵1和基阵2所确定方位线的公垂线, 公垂线AB的中点O作为声源解算点。
以图1中六元阵为例, 根据TDOA原理[11]以及基阵与目标的几何关系来推导定向公式。由笛卡尔坐标系可知:
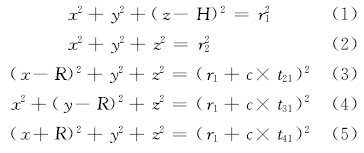
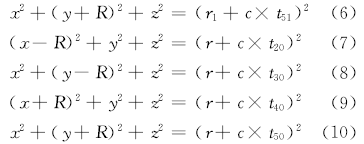
现将式(3)减去式(5), 式(4)减去式(6), 式(7)减去式(9), 式(8)减去式(10), 可得:
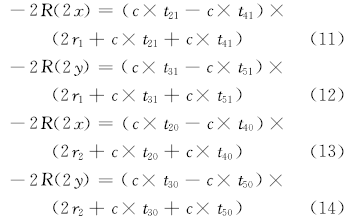
现将式(1)分别减去式(3)(4)(5)和(6), 可得:
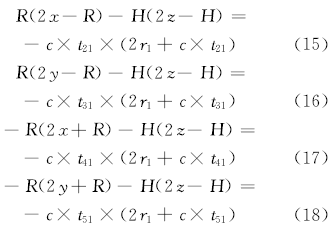
式中:t21、t31、t41及t51表示节点2、3、4、5相对于声源到节点1的时延差; t20、t30、t40及t50表示节点2、3、4、5相对于声源到节点0的时延差; c为声速; H为高度差; R为孔径; r1为声源到节点1的距离; r2为声源到节点0的距离。φ 为方位角; θ 为俯仰角。
式(11)加式(13)可得x的表达式, 式(12)加式(14)可得y的表达式。联立式(15)(16)(17)和(18)可得z的表达式。
基于平面波假设[12, 13], 容易推导出基阵的定向公式:
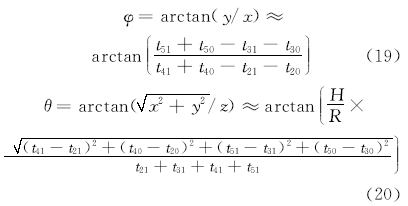
由式(19)(20)可知, 该算法消除了声速的影响。在确定方位线之后, 通过求两条方位线的公垂线的中点, 即可完成对声源点坐标的解算。至于时延的估计, 有很多方法, 例如广义互相关法、互功率谱相位法、自适应滤波法和参量模型法等[14, 15, 16], 在此不做深入探讨。
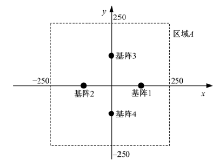
布设方案如图2所示, 在区域A中, 4个六元阵的基阵中心分别位于x、y轴上, 其中, 基阵1中心坐标为(Q, 0, 0); 基阵2中心坐标为(0, Q, 0); 基阵3中心坐标为(-Q, 0, 0); 基阵4中心坐标为(0, -Q, 0)。其中Q为正数, 单位为m。
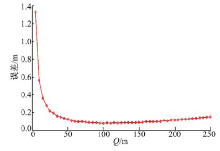
在图2的区域A中, 基阵i与基阵j的交汇结果为Pij, 其中i、j取值为1, 2, 3, 4。由于4个基阵两两交汇, 可以得到6个不同的解算值, 令声源坐标的初始解算值等于这6个解算值的均值, 即(P12+P13+P14+P23+P24+P34)/6。在区域A中, 通过使声源点坐标遍历区域A的每一点, 对于不同Q的取值, 计算声源点遍历区域A的坐标x的平均误差、坐标y的平均误差和坐标z的平均误差, 然后将坐标x、坐标y和坐标z的误差取平均值称作在当前Q值条件下, 声源点在区域A的区域误差均值。图3为Q值在5~250 m间变化时的区域误差均值, 步长为5 m, 蒙特卡洛次数为500次, 取时延标准差为60 ms。
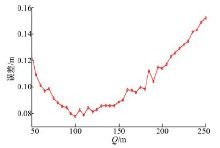
由于Q在50 m以内时, 误差比较大, 以致在Q大于50 m后的误差分布不能够被清晰地辨别, Q在50~250 m内变化时, 声源点的区域误差均值分布如图4所示。
由图4可知, 在Q=100 m时, 声源点在区域A的区域误差均值最小。因此, Q的最优取值为100 m。同理在区域A内, 通过区域误差均值最小原理可以得出:高度差的最优取值为1.5 m; 孔径的最优取值为2.1 m; 边界的最优取值为21 m。
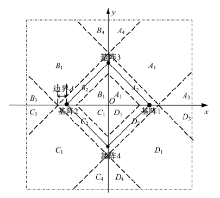
定位区域划分如图5所示, 将整个区域划分为16块。分别是第一象限的A1、A2、A3和A4, 第二象限的B1、B2、B3和B4, 第三象限的C1、C2、C3和C4以及第四象限的D1、D2、D3和D4。其中d为边界。
以第一象限的区域为例:
A1:{(x≥ 0)& & (y≥ 0)& &
(y> -x+d+Q||y< -x+d-Q)& &
(y> x-d-Q)& & (y< x+d+Q)}
A2:{(x≥ 0)& & (y≥ 0)& &
(y< -x+d+Q||y> -x+d-Q)}
A3:{(x≥ 0)& & (y≥ 0)& & (y≤ x-d-Q)}
A4:{(x≥ 0)& & (y≥ 0)& & (y≥ x+d+Q)}
区域B、C和D可参照A进行区域划分。
基于区域划分的声定位算法步骤如下:首先, 通过声传感器进行数据采集; 之后, 对数据信息进行时延特征的提取; 然后, 根据1.1节中的公式进行定向解算; 进而, 确定4条方位线, 这4条方位线可以确定6个交汇定位结果, 以这6个定位结果的均值作为定位初始值; 最后, 根据初始值判断声源的具体区域, 并根据声源所处区域进行更为精确的解算。
针对每个区域的具体解算方法如下:
区域A1:采用基阵1和基阵2交汇解算。
区域A2:如果初始声源解算值到x轴的距离大于其到y轴的距离, 采用基阵1和基阵2交汇解算; 反之, 则采用基阵3和基阵4交汇解算。
区域A3:采用基阵3和基阵4解算声源的x坐标, 基阵1和基阵3解算声源的y坐标和z坐标。
区域A4:采用基阵1和基阵3解算声源的x坐标和z坐标, 采用基阵1和基阵2解算声源的y坐标。可根据对称性得出在其他区域的声源解算值。
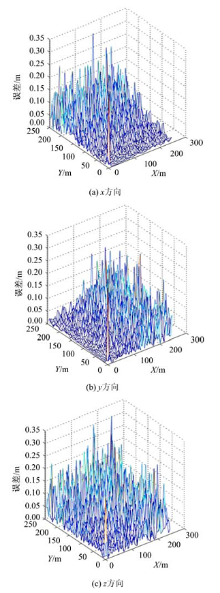
在区域A中, 由于阵型布置关于原点对称, 为方便计算这里只取区域A的第一象限进行误差分析。按1.2节进行参数布设。令时延标准差为60 μ m, 蒙特卡洛次数为500次, 声源坐标的误差分布图如图6所示。
由图6可知:坐标x和y的误差最大值不超过0.35 m, 坐标z的误差最大值不超过0.2 m。
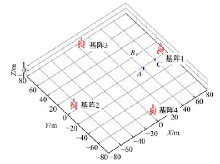
以炮竹作为声源, 在北京的郊区的一块200 m× 200 m的定位区域中随机选取3个声源点, 每个点重复做3次实验。基阵布设及声源位置如图7所示。
这3个点的坐标分别是A(35.9360, -7.8415, -0.2058)、B(57.1430, -4.7435, -0.3748)和C(44.4280, 15.3805, -0.2788)。实验中采用基于ZigBee技术的JN5148模块进行数据采集, 声传感器采用市场中廉价的麦克风模块。由于实验区域受限, 通过求取区域误差均值最小的原理可以得出高度差的最优取值为1.3 m, 孔径的最优取值为1.8 m, 边界的最优取值为11 m, 基阵1和基阵2间距为70 m, 基阵3和基阵4间距为70 m。
按如上参数配置4个基阵, 随机选择的3个声源点的定位结果如表1所示。
| 表1 三个声源点的坐标误差 Table 1 Errors comparison of three sound sources |
由表1可知, 虽然受环境误差的影响, 每个点的3次实验结果出现了波动, 但这9组数据表明空间交汇阵的定位精度均在1 m以内。
本文提出的基于区域划分的空间交汇阵不仅有效地消除了声速对定位算法的影响, 而且解决了交汇阵中心阵元连线附近区域误差大的问题。声源定位区域以区域误差均值判定准则, 选择基阵高度差、孔径、边界及阵间距等阵元参数的最优解, 并将定位区域划分为16个子区域, 在每个子区域选取不同的定位算法。如果采用不同的基阵类型和数量, 则需要重新对定位区域进行划分。通过仿真和实验数据分析可以看出, 使用该定位算法对提高声源定位精度具有很大的实用价值。由于受场地的限制, 在200 m× 200 m的区域进行实验, 声源坐标的定位精度都在1 m以内。未来需要进行更大场地规模的测试, 以验证基于区域划分的空间交汇阵定位算法的定位精度。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|