飞行时间质谱(Time-of-flight mass spectrometry, TOF-MS)技术是一种重要的物质分析手段, 具有消耗样品少、检测速度快、质量范围无限制等优点, 广泛应用于化学、半导体、生物、宇宙科学等领域^{[1, 2]}。TOF-MS大部分时间被用于物质的定性分析, 但近年来其定量分析也逐渐成为研究热点之一^[3]。受仪器分辨率限制, 一些质量数接近的离子不能被分离, 形成重叠谱峰, 无法获得定量分析所需的位置、幅度、峰形及面积等重要参数, 需要对其进行分离, 从而为定量分析奠定基础。

目前TOF-MS重叠谱峰分析方法主要有两大类:第一类为数学变换找特征点, 如导数阈值法^[4], SNR分析法^[5], 连续、离散小波分析法^[6]等; 第二类为标准函数模型匹配法, 其采用Gaussian函数^[7]、多项式^[8]、Lorentzian函数^[9]或混合模型^{[10, 11]}去匹配TOF-MS谱峰序列。这两类方法解决了TOF-MS谱峰识别, 自动化处理等问题, 大大提高了仪器效率及检测准确性。但定量分析时, 这些方法又存在各自的不足:第一类方法采用一定数学变换手段, 确定质谱峰的起止、极值等畸变点, 获得位置、峰高等信息, 并不能还原峰形。第二类方法根据谱峰与现有已知函数的形态相似特点, 建立匹配模型, 模型的确立需要求解若干参数。如果峰形形态与匹配模型一致, 该方法可以分离谱峰, 得到峰形信息, 但形态存在差异, 尤其谱峰为非对称时, 该方法会丢失信息。TOF-MS的谱峰代表着不同时刻到达检测器的离子数量, 为保证定量准确性, 任何峰形信息都不应被舍弃。

针对上述问题, 本文提出一种基于特征峰形匹配的TOF-MS重叠谱峰分离方法, 方法可有效分离重叠谱峰, 尤其对非对称重叠峰效果明显。

TOF-MS离子(尤其质量数接近的离子)运行轨迹基本相同, 在谱图上体现为:临近谱峰, 峰形相似。仪器长时间工作时, 信号峰形可能变化, 发生畸变, 形成非对称, 但变化过程中, 相临近谱峰的峰形仍然保持一致。本文方法基于这一原理, 提取重叠峰附近若干单峰的形态特点, 形成特征峰, 再用特征峰去匹配重叠峰, 对其进行分离。如果采用传统标准模型匹配法, 当峰形发生改变时, 函数模型固定, 会产生匹配失真, 本文方法中特征峰会随着峰形变化而改变, 适应性更好, 尤其对TOF-MS常见的非对称峰重叠峰, 效果明显。

特征峰的提取是本文方法的关键所在, 其由重叠峰附近的若干单峰计算获得, 每个单峰位置准确性直接影响特征峰的形态, 而噪声对峰位置判定影响较大, 所以要对原始谱进行消噪处理。研究人员认为TOF-MS理论峰形接近高斯曲线^{[7, 10, 11]}, 如式(1)所示, 采用高斯曲线与原始谱峰进行相关运算, 以达到消噪的目的。

RGS(τ)=∫-∞+∞G(t)S(t+τ)dt(1)

式中:G(t)为高斯函数; S(t+τ )为原始谱峰数据; R_GS (τ )为运算处理后的谱峰。

相关运算可使与高斯曲线形态接近的有用信号增强, 噪声则被衰减, 从而到达消噪的目的。谱峰信噪比得到改善后, 设定阈值, 可以找到峰位置, 统计各谱峰宽度, 本文采用半高峰宽(Full width at half maximum, FWHM)代表谱峰宽度。因为谱图中大部分为单峰, 所以峰宽集中处为仪器的有效峰宽, 该宽度的峰被认为是单峰, 而较宽的峰则为重叠峰。

在重叠峰附近选取单峰, 选取原则为“ 择高弃低” , 因为高峰受噪声影响小, 信噪比相对更好。式(2)为特征峰的计算方法, 其由选取的单峰加权叠加产生。

F(t)=∑i=1nμiPeaki(t)(2)

式中:F(t)为特征峰; Peak_i(t)为所选取的单峰原始信号; μ _i为叠加的权系数, μ _i值与所选单峰到重叠峰的距离有关, 这是因为峰位置越近, 峰形相似程度越高, μ _i值相应也越大。特征峰需要被归一化, 有利于后期计算。

特征峰确定后, 再利用原谱图数据与特征峰构造功率谱密度函数, 如式(3)所示, 该函数代表重叠谱峰与特征峰吻合程度, 程度越高说明重叠谱中某一单峰含量越大。当吻合程度最高时, 功率谱密度函数最小, 说明已经匹配出一个峰。按照功率谱密度函数最小原则, 以先大峰后小峰的顺序, 从重叠峰中分离出两个单峰, 达到谱峰分离的目的。

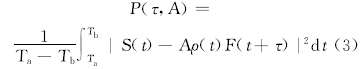
式中:P(τ , A)为构造的功率谱密度函数; S(t)为原始重叠谱峰; T_a 、T_b为积分时间区间, 积分方向由大峰区向小峰区进行; A为特征系数, 反映重叠峰的峰高; τ 为谱峰位置, 当功率谱密度函数最小时, 可以匹配出其中一峰, 获得该峰的特征系数A和位置τ , 再利用特征峰即可重构该峰; ρ (t)为边缘系数, 定义如下:

ρ(t)=expαMdhMHWt(4)

式中: h为重叠峰的峰高比; M_d为峰间距估计; M_HV为谱峰半峰宽; α 为校准系数, 边缘系数可加强重叠峰边缘信号对功率谱密度函数的影响, 因为这部分信号更接近实际有效峰形。

可根据功率谱密度函数确定重叠峰的分离情况, 如式(5)所示, 其中 ε为信号本底信号功率密度, M为调节系数, 当谱峰重叠时, 去除某一峰的含量, 其功率密度仍会大于 Mε,因为残存有效功率信号。这时, 需要通过计算去除该峰的功率谱密度函数, 剔除另一峰, 功率谱密度函数则会小于 Mε,重叠谱峰也被完全分离。

P(τ, A)> MεP(τ, A)≤Mε(5)

以特征谱峰作为基谱峰, TOF-MS一定质量数范围内全谱可认为是特征峰的线性组合, 如式(6)所示, 其中A_i 为第i个峰幅度, τ _i 为第i峰位置, W(t)则表示一定质量数范围内全谱。

W(t)=∑i=1mAiF(t+τi)(6)

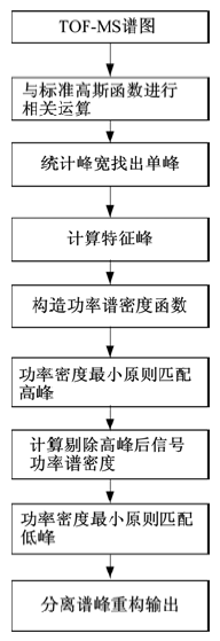
本文方法的具体流程如图1所示, 根据该方法, 利用功率谱密度函数最小原则, 可获得重叠峰中每个单峰的位置和幅度, 再利用特征峰对其重构, 输出分离谱峰。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 本文方法实施流程Fig.1 Flow chart of proposed method

受离子能量分布、聚焦透镜、反射镜、检测器等因素影响, 非对称峰在TOF-MS较为常见, 非对称情况下重叠峰匹配的准确性, 直接影响定量分析精度。分析本文方法在不同对称程度情况下, 对TOF-MS谱峰的分离能力, 并与Gaussian、Lorentzian两种匹配方法进行对比。

采用对称系数量化TOF-MS谱峰对称程度, 根据文献^[9], 将对称系数定义为:

δ=HWHMrightHWHMleft-1(7)

式中:HWHM_right是右半峰50%峰高处的宽度; HWHM_left为左半峰50%峰高处的宽度; δ 值的大小反应峰形的对称程度。

Coombes等^[12]根据TOF原理建立了数据仿真模型, 将模型中离子初始能量由正态分布改为分段正态分布, 即左、右两半部分函数选择不同标准差σ,可通过调节σ大小, 模拟出不同对称性的谱峰数据。因模型对检测器噪声估计不足, 在信号中加入一定功率的白噪声, 与实测数据更为接近。

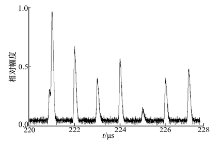
由仿真模型得到TOF-MS谱图数据(见图2), 采用特征峰匹配法, 需要保证谱峰形态相似, 质量范围不宜太大。这里, 选取的7个仿真谱峰, 全部分布在8个质量数范围内。由图2可见, 第1个为重叠峰, 其余6为单峰, 数据的信噪比为12.4。采用后6个单峰计算特征谱峰, 分离重叠峰。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 TOF-MS原始仿真谱图Fig.2 Original spectrum simulation of TOF-MS

2.1 特征峰确定

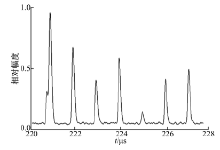
用高斯曲线与原始谱峰做相关运算, 将随机噪声滤除, 提高信噪比, 图3为消噪后的谱图。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 与高斯曲线相关运算所得谱图Fig.3 Spectrum of correlation operation between Gaussion curve and original data

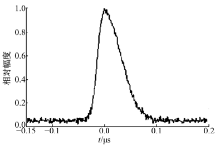
对比图2和图3可以看出:信噪比明显改善, 后6个单峰宽度基本一致, 其峰宽窄于重叠峰。设定阈值, 确定峰位置, 按照本文方法利用后6个单峰得到特征峰, 如图4所示。叠加所用的单峰数据应为原始信号, 而不是消噪后的信号, 因为相关运算后信号失真较大, 不适合用其计算特征峰。

从图4可以看出, 谱峰存在非对称现象, 左半峰窄于右半峰, 因为叠加的效果, 信噪比优于原始信号。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 提取的特征峰Fig.4 Characteristic peak of proposed method

2.2 分离效果

采用分离度这一概念量化描述重叠峰的分离水平, 李宝强等^[13]最先将其引入质谱领域, 定义如下:

R=C2-C10.5(W1+W2)(8)

式中:C₁、C₂分别是两峰的位置; W₁、W₂分别为两峰10%峰高处的宽度; R为分离度, 分离度越大, 说明仪器分辨率越高。

分析在对称系数为0.2、0.6、1.0、1.6情况下Gaussian法、Lorentzian法及本文方法的实施前后分离度变化, 如表1所示。

表1

Table 1

表1(Table 1)

表1 不同方法对称系数改变时的分离度 Table 1 Resolutions of different methods when asymmetry index changed δ 原始分离度 Gaussian Lorentzian 本文方法 0.2 0.428 0.697 0.637 0.685 0.6 0.432 0.692 0.614 0.665 1.0 0.416 0.645 0.586 0.652 1.6 0.403 0.624 0.601 0.619

表1 不同方法对称系数改变时的分离度 Table 1 Resolutions of different methods when asymmetry index changed

从表1中可看出, 不同对称性情况下的分离效果, 3种方法都可提高分离度, 其中Gaussian法与本文方法分离水平相当, Lorentzian法稍差。当对称系数增大时, 3种方法分离度都会变差, 但仍基本一致。分离度只能说明分离后的峰宽, 不足以完全展示分离的准确性。为更好地说明对称性对分离效果的影响, 给出δ =0.2和δ =1.6时, Gaussian法、Lorentzian法和本方法分离前、后的谱峰对比, 如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 不同方法在δ =0.2和δ =1.6时的匹配效果Fig.5 Separated peaks of different methods when δ =0.2 & δ =1.6

图5(a)~(f)中, 外侧实线为重叠谱峰, 内侧虚线代表分离后的低矮峰和高峰。从图5(a)(d)可见, Gaussian法在δ =0.2时峰高、位置、峰形等效果较好, 但δ =1.6时, 低矮峰的峰高及形态都出现较大误差, 谱峰吻合程度不高。由图5(b)(e)可见, Lorentzian法在δ =0.2时匹配效果虽略逊于Gaussian法, 但也能获得峰高、位置、峰形等信息, 而在δ =1.6时, 低矮峰的峰高和形态均没能恢复, 谱峰吻合程度较差。由图5(c)(f)可见, 本方法在δ =0.2时匹配效果与Gaussian法相当, 峰高、位置、峰形等信息恢复较好。而当δ =1.6时, 本方法匹配效果明显好于前两者, 与之相比, 基本能把峰高、位置及形态等信息恢复, 峰形吻合程度良好, 低矮峰也能正常还原。另外, 重叠峰为两个单峰的叠加, 高于任何一个单峰(重叠峰上每点的高度, 都为两个单峰高度之和), 采用本文方法在图5(f)中可以看到这一现象。可见, 在处理非对称峰时, 本文方法不论在重要峰参数还原, 还是峰形吻合程度均优于前两者。

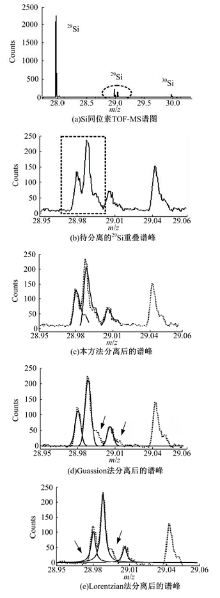
硅是地壳的主要组成元素之一, 其同位素分析是地球化学领域的重要研究内容^{[14, 15]}, 但测量易受同质峰干扰。自然界中²⁸Si的含量比²⁹Si和³⁰Si高20倍以上, 测定²⁹Si时经常收受到同质峰²⁸Si¹H干扰。

锆石是常见的一种晶体矿物, 主要成分为ZrSiO₄, 在地质定年、示踪等方面有重要作用。本文采用中国地质科学院北京离子探针中心自主研发的飞行时间二次离子质谱仪调试样机, 测定锆石中Si同位素丰度, 需要将²⁹Si和²⁸Si¹H的重叠峰分离。测得Si的三个同位素谱峰如图6(a)所示, ²⁹Si附近存在重叠峰, 图6(b)为²⁹Si附近谱峰的展开, 其中方框内为重叠峰, 包含²⁹Si和²⁸Si¹H两个单峰。方框外为另外两个单峰, 存在非对称现象, 观察该附近质量数的其他谱峰, 均为非对称。采用本文方法分离该重叠峰的效果如图6(c)所示, 经计算, 可使其分离度由0.371升至0.519, 提高39.9%。

图6(c)(d)(e)分别为本文方法、Gaussian法及Lorentzian法对²⁹Si、²⁸Si¹H重叠峰分离效果, 其中, 虚线为未分离的重叠峰, 左起第一实线为分离后的²⁹Si峰, 第二实线为分离后的²⁸Si¹H峰。从分离谱峰底部可以看出Gaussian法和Lorentzian法不能完全吻合(箭头所示), 整块谱峰被“ 消掉” , 这在TOF-MS定量分析中影响较大。本文方法峰底部吻合较好, 但²⁸Si¹H峰顶未能完全吻合, 这是因为²⁸Si¹H峰叠加进了前面²⁹Si峰的峰尾部分, 导致重叠谱峰高于单峰。由于实验测得的Si同位素附近谱峰的峰形与Gaussian、Lorentzian两种函数存在差异, 本文方法存在优势, 在分离谱峰的同时可基本还原峰形信息。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 3种方法29Si与28Si1H重叠谱峰分离前后效果对比Fig.6 Results of 29Si & 28Si1H overlapped peak separation by three methods

根据“ TOF-MS质量数相近的谱峰, 峰形相似” 的特点, 提出了一种基于特征峰匹配的重叠谱峰的分离方法。当峰形对称性较好(δ =0.2)时, 该方法分离效果与Gaussian、Lorentzian匹配法基本相同, 但对称性变差(δ =1.6)时, 该方法处理效果明显优于后两者。采用本文方法对实测²⁹Si和²⁸Si¹H的重叠谱峰进行分离, 分离度由0.371升至0.519, 提高39.9%, 可基本还原峰形信息。