用于TOF-SIMS的锆石样品图像自动聚焦算法

引用本文

王培智, 田地, 龙涛, 李抵非, 邱春玲, 刘敦一. 用于TOF-SIMS的锆石样品图像自动聚焦算法. 2017, 47(1): 308-315
WANG Pei-zhi, TIAN Di, LONG Tao, LI Di-fei, QIU Chun-ling, LIU Dun-yi. Automatic focusing algorithm for TOF-SIMS zircon sample image. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 308-315 复制到剪切板

Permissions

用于TOF-SIMS的锆石样品图像自动聚焦算法

王培智¹, 田地¹, 龙涛², 李抵非³, 邱春玲¹, 刘敦一²

1.吉林大学仪器科学与电气工程学院,长春 130061

2.中国地质科学院地质研究所北京离子探针中心,北京 102206

3.中国计量科学研究院,北京 100029

通讯作者:龙涛(1984-),男,副研究员.研究方向:质谱仪器研制与应用.E-mail:longtao@bjshrimp.cn

作者简介:王培智(1987-),男,博士研究生.研究方向:二次离子质谱技术.E-mail:wangpeizhi840923@163.com

基金:国家重大科学仪器设备开发专项项目(2011YQ05006902).

摘要

为满足现代二次离子质谱仪(SIMS)锆石样品图像自动聚焦系统对聚焦准确度的要求,提出了一种具有自动消除噪声功能的锆石样品图像自动聚焦算法,并将其应用于飞行时间二次离子质谱仪(TOF-SIMS)。该算法包括锆石图像识别分割法、分段式聚焦算法和调焦控制策略。在聚焦远峰区,采用Roberts算子的聚焦评价函数及差分累加的调焦控制策略进行粗调;在聚焦近峰区,捕捉图像中的锆石目标进行识别分割,采用局部坐标算子的聚焦评价函数与爬山法相结合的调焦控制策略进行聚焦细调。实验结果表明:该算法聚焦准确率达99%,可有效抑制噪声干扰,实现了对锆石样品图像的自动、准确聚焦。

关键词: 自动控制技术; 分段式聚焦算法; 图像识别; 图像分割; 飞行时间二次离子质谱仪

中图分类号:TH84 文献标志码:A 文章编号:1671-5497(2017)01-0308-08

Automatic focusing algorithm for TOF-SIMS zircon sample image

WANG Pei-zhi¹, TIAN Di¹, LONG Tao², LI Di-fei³, QIU Chun-ling¹, LIU Dun-yi²

1.College of Instrumentation and Electrical Engineering, Jilin University,Changchun 130061, China

2.Beijing SHRIMP Center, Institute of Geology,Chinese Academy of Geological Sciences, Beijing 102206,China

3.National Institute of Metrology, Beijing 100029,China

Abstract

In order to satisfy the requirement of focusing accuracy of modern Secondary Ion Mass Spectrometer (SIMS)'s zircon sample image auto focusing system, an algorithm that automatically removes noise is proposed and applied to the Time-of-Flight (TOF)-SIMS. The proposed algorithm includes zircon image recognition and segmentation, a secondary-type focusing algorithm, and a focusing control strategy. A Roberts function and a differential accumulation focusing control strategy are used for coarse tuning in area far from the peak. In the near-peak region, the zircon image is captured and segmented from the background. A local coordinate function and hill climbing method are then used for fine tuning. A series of experiments show that the proposed algorithm has an accuracy rate of 99% and can effectively restrain noise interference, enabling the automatic focusing of zircon sample images.

Keyword: automatic control technology; sectional type focusing algorithm; image recognition; image segmentation; time of flight-secondary ion mass spectrometer(TOF-SIMS)

Show Figures

0 引言

锆石U-Pb定年是同位素年代学研究中最常用和有效的方法之一^{[1, 2]}。二次离子质谱仪(Secondary ion mass spectrometer, SIMS)作为高分辨、高精度的表面分析仪器, 可以在锆石样品上数微米的范围内获取精确的同位素及化学组成信息, 是一种无需对样品进行化学处理和近于无损伤的分析技术, 非常适用于变质增生壳厚度只有数微米的锆石样品的微区原位分析^{[3, 4, 5]}。SIMS仪器的光学成像系统采集锆石样品图像并将其显示给实验操作人员。高效、准确的自动聚焦算法可以使锆石图像处于最佳观测状态, 为后续样品图像的自动选点、仪器的自动化运行等提供保障。

目前国际上主要对锆石样品进行分析的SIMS仪器有澳大利亚的Shrimp系列、法国CAMECA的IMS-1280系列等, 这些仪器的自动聚焦系统采用以传统图像边缘检测算子为核心的算法。锆石样品图像的噪声来源主要有CCD相机产生的电噪声、样品靶表面不平整产生的图像噪声等, 这些噪声均会影响自动聚焦系统运行时的准确度^[6]。以传统图像边缘检测算子为核心的自动聚焦算法无法有效地抑制噪声干扰^[7], 这些干扰会导致图像聚焦位置不准确, 聚焦位置不准确会造成SIMS仪器的一次离子束实际轰击点与图像显示点存在位置偏移, 影响仪器采集数据的准确性。李抵非博士^[8]在2012年基于原有SIMS仪器平台, 提出一种以改进的拉普拉斯(Laplace)算子为核心的具有抗干扰能力的自动聚焦算法, 实现了锆石图像的准确聚焦。随着地球科学和宇宙科学的快速发展, 近年来研制的SIMS仪器已经拥有更小的一次离子束斑(几微米甚至于亚微米级别), 更精密的样品移动台(亚微米级别), 自动聚焦系统聚焦位置几微米的偏移量就可能导致一次离子束斑轰击位置等数量级的偏差, 这对锆石微区原位分析的实验数据准确性会产生较大影响, 基于原有SIMS平台搭建的锆石自动聚焦系统已经不能满足现代SIMS仪器对聚焦准确度的要求, 这就给锆石样品图像自动聚焦系统提出了更高的挑战。

为满足现代SIMS锆石样品图像自动聚焦系统对聚焦准确度的要求, 本文提出一种具有自动消除噪声功能的锆石样品图像自动聚焦算法。该算法包括从细胞图像处理技术引入的图像识别分割法、带有自动消除噪声功能的分段式聚焦评价函数以及具有普遍适用性的调焦控制策略。本文算法已在中国地质科学院地质研究所研发的飞行时间二次离子质谱仪(Time of flight-SIMS, TOF-SIMS)上测试使用, 实现了对锆石样品图像的自动准确聚焦。

1 算法设计

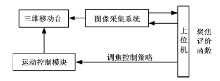
自动聚焦系统的原理框图如图1所示, 锆石样品由一个位移精度为0.1 μ m的三维移动台承载, 锆石样品图像通过一套光学图像采集系统采集给上位机进行处理, 上位机根据图像的清晰程度给出相应的指令控制三维移动台在聚焦轴方向上移动, 最终使图像达到聚焦。系统的关键技术包括:锆石图像的识别和分割, 聚焦评价函数和调焦控制策略。锆石图像的识别和分割是将锆石图像与背景图像进行分离; 聚焦评价函数是用来评价当前图像的清晰度; 调焦控制策略是控制三维移动台移动搜索聚焦点的手段。

	Figure Option View Download New Window
	图1 自动聚焦系统原理图Fig.1 Schematic diagram of automatic focusing system

1.1 锆石图像识别及分割设计

锆石图像的内容可以分为背景图像和目标图像。目标图像为锆石样品, 背景图像为样品承载树脂, 样品承载树脂由于其制作时已保证其平整性, 在整个聚焦过程中, 其梯度的变化值一般很小, 所以在图像位于聚焦点附近时, 可采用图像识别分割的办法将锆石样品图像从背景图像中分割出来, 同时避免了背景噪声的干扰。

图2(a)为系统采集的锆石样品灰度图像, 首先使用灰度增强和维纳滤波对锆石图像进行预处理。其次使用灰度梯度算子来计算图像的边缘和阈值, 然后在原阈值的基础上修改阈值使检测到的边缘更合理, 以获得更精确的图像边缘, 如图2(b)所示。

	Figure Option View Download New Window
	图2 锆石样品图像识别及分割示意图Fig.2 Schematic diagram of recognition and segmentation of zircon samples

二值梯度图像的线条显示了图像中锆石边缘比较高的对比度, 但与原图像相比, 可以看见目标锆石图像中的线条并不连续, 含有间隙。采用线性结构元素分别在垂直方向和水平方向对这些不连续的线条进行膨胀, 如图2(c)所示, 图像的边缘线条已趋于连续。

膨胀后的二值图像可以比较精确地显示锆石的轮廓, 但是在膨胀后的图像中, 锆石的内部仍有空洞, 采用填充的方式将锆石图像填充出来, 如图2(d)所示。

图像中检测到的锆石图像有多个, 靠近图像边界的锆石图像并不是一个个完整的图像, 采用去除边界的方式, 将非感兴趣的目标图像扣除掉, 清除掉的图像效果如图2(e)所示。

清除掉边缘目标后的图像并不光滑, 使用菱形结构元素对目标图像进行腐蚀, 腐蚀后得到的最终识别的图像如图2(f)所示。将图像中白色像素点的区域分割出来进行计算, 可以大大提高系统的抗噪性。本文所设计的这种图像分割方式适合于具有封闭边缘特性的目标图像, 如生物领域的细胞分割图像学^{[9, 10]}等。

1.2 分段式聚焦算法的设计

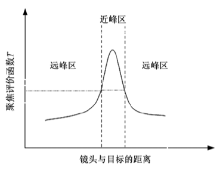
理想的聚焦评价函数, 从图像模糊区到图像聚焦区, 其聚焦评价函数的曲线应接近指数函数曲线的变化过程, 本文将图像模糊区称为聚焦远峰区, 图像清晰区称为聚焦近峰区, 下文将以“ 远峰区” 、“ 近峰区” 代指图像的模糊和清晰区。如图3所示^[8], 图像处于远峰区时, 函数的斜率较小, 代表聚焦评价函数值的变化较为缓慢。而在图像的近峰区, 函数的斜率较大, 聚焦评价函数值变化较快。若在远峰区和近峰区均采用一种聚焦评价算子进行图像的梯度计算, 极易受到噪声的干扰, 造成误聚焦。若设置一适当的阈值 $\begin{matrix} T \end{matrix}$ 将聚焦评价函数合理地分为两段, 在远峰区采用运算速度较快的算子, 在近峰区采用抗噪性较强的算子, 就可以发挥不同算子的优势, 取得更好的效果^[8]。

	Figure Option View Download New Window
	图3 理想聚焦评价函数曲线图Fig.3 Ideal focusing evaluation function curve

目前的聚焦评价函数多采用灰度梯度法^{[11, 12, 13]}。其中, 最常用的有灰度差分绝对值算法、Roberts梯度算法、Sobel算法以及采用拉普拉斯算法的梯度函数算法。以上几种算法中, 灰度差分绝对值响应速度最快, 而Roberts梯度算法次之, 但它们单峰性相对较差, 抗噪声能力相对弱, 适合聚焦粗调。拉普拉斯算子方法是一种二阶导数算子, 单峰性良好, 但其对噪声比较敏感。

针对以上函数不同的特性, 本文在远离聚焦峰值的区域采用以Roberts梯度算子为核心的聚焦评价函数的算法:

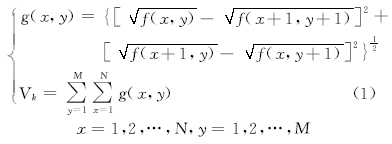
式(1)是Roberts算法的数学表达, 设置一适当的阈值T, 当算子计算出聚焦评价函数在位置k处的值V_k< T时, 图像处于远峰区; 当 $\begin{matrix} V_{k} \geq T \end{matrix}$ 时, 图像进入近峰区。这种算子可以发挥其运算速度快的优点, 可用在远峰区进行粗调。

在进入聚焦评价函数近峰区时, 传统的灰度梯度算子无法有效识别图像边缘并且不能去除灰度变化缓慢区域内的大梯度噪声, 李抵非博士^[8]设计的改进型Laplace算子虽能在一定程度上抑制噪声干扰, 但其应用背景是一次离子束斑直径为20~30 μ m的传统SIMS仪器, 且其聚焦轴方向上的样品移动台的最小步进为4 μ m, 而TOF-SIMS仪器的一次离子束斑直径已经达到5 μ m以下, 样品移动台的最小步进为0.1 μ m, 这种改进型算法已不能满足TOF-SIMS对聚焦精度的需求。鉴于此, 作者采用了一种基于局部坐标二次微分^{[14, 15]}的边缘检测算子, 使得上述问题得以有效的解决。如图4所示, 局部坐标系定义如下:ξ 表示图像边缘垂直于梯度矢量的方向; η 表示图像边缘的梯度方向; u(x, y)表示图像边缘曲线函数。

	Figure Option View Download New Window
	图4 局部坐标系示意图Fig.4 Schematic diagram of local coordinate system

其中:

$\begin{matrix} \{\begin{matrix} η = \frac{\nabla u}{|\nabla u|} = (cosθ, sinθ) \\ ξ = (- sinθ, cosθ) \end{matrix} \end{matrix}$ (2)

在这一局部坐标系中有:

$\begin{matrix} \frac{\partial u}{\partial ξ} = 0, \frac{\partial u}{\partial η} \geq 0 \end{matrix}$

故在这一局部坐标系下:

$|\nabla u| = \sqrt[]{{(\frac{\partial u}{\partial η})}^{2}} = \frac{\partial u}{\partial η}$ (3)

从而：

$\frac{\partial |\nabla u|}{\partial η} = \frac{\partial^{2} u}{\partial η^{2}}$

根据定义, $\begin{matrix} \frac{\partial |\nabla u|}{\partial η} \end{matrix}$ 是梯度 $\begin{matrix} \nabla (|\nabla u|) \end{matrix}$ 的 $\begin{matrix} η \end{matrix}$ 分量, 故:

$\frac{\partial |\nabla u|}{\partial η} = \nabla (|\nabla u|) \cdot η = \nabla (|\nabla u|) \cdot \frac{\nabla u}{|\nabla u|}$ (4)

而：

$\nabla (|\nabla u|) = \nabla (\sqrt[]{u_{x}^{2} + u_{y}^{2}}) = \{\frac{u_{x} u_{xx} + u_{y} u_{yy}}{\sqrt[]{u_{x}^{2} + u_{y}^{2}}}, \frac{u_{x} u_{xy} + u_{y} u_{yy}}{\sqrt[]{u_{x}^{2} + u_{y}^{2}}}\}$ (5)

由式(4)(5)推出:

$u_{ηη} = \frac{\partial |\nabla u|}{\partial η} = \frac{u_{x} (u_{x} u_{xx} + u_{y} u_{xy}) + u_{y} (u_{x} u_{xy} + u_{y} u_{yy})}{{|\nabla u|}^{2}} = \frac{u_{xx} u_{x}^{2} + 2 u_{x} u_{y} u_{xy} + u_{yy} u_{y}^{2}}{{|\nabla u|}^{2}}$ (6)

另由于：

$Δu = u_{xx} + u_{yy} = u_{ξξ} + u_{ηη},$

$u_{ξξ} = Δu - u_{ηη} = \frac{u_{xx} u_{x}^{2} - 2 u_{x} u_{y} u_{xy} + u_{yy} u_{y}^{2}}{{|\nabla u|}^{2}}$ (7)

定义局部坐标差分算子形式如下:

$\begin{matrix} Div = |\frac{u_{ηη}}{u_{ξξ}}| \end{matrix}$ (8)

由式(6)(7)知:

$\begin{matrix} \begin{matrix} u_{ξξ} = \frac{u_{xx} u_{y}^{2} - 2 u_{xy} u_{x} u_{y} + u_{yy} u_{x}^{2}}{{|\nabla u|}^{2}}, \\ u_{ηη} = \frac{u_{xx} u_{x}^{2} + 2 u_{xy} u_{x} u_{y} + u_{yy} u_{y}^{2}}{{|\nabla u|}^{2}} \end{matrix} \end{matrix}$

式中:u_{ξ ξ} 、u_{η η}分别表示图像边缘曲线函数u(x, y)在局部坐标(ξ , η )中沿等图像边缘曲线的切向和法向的二次微分。

	Figure Option View Download New Window
	图5 算子对图像的运算示意图Fig.5 Schematic diagram of operator for image operation

由式(8)所确定的局部坐标算子可以得出本算法有以下特性:

(1)如图5(a)所示, 在图像边缘区:u_ηη较大, u_ξξ较小, u_ηη/u_ξξ数值较大, 即算子Div较大, 表示其可以很好地保留图像的边缘信息。

(2)如图5(b)所示, 在图像平坦区:u_ηη和u_ξξ均较小, u_ηη/u_ξξ数值接近1, 即算子Div也较小, 不会出现局部极值。

(3)如图5(c)所示, 在孤立噪区去:u_ηη和u_ξξ均较大, u_ηη/u_ξξ数值接近1, 即算子Div也较小, 可以有效去除孤立噪声点的干扰。

对本局部坐标算子采用中心差分方式进行离散化近似, 其中:

$\begin{matrix} \begin{matrix} u_{x} = \frac{f_{i, j + 1} - f_{i, j - 1}}{2}; \\ u_{y} = \frac{f_{i + 1, j} - f_{i - 1, j}}{2}; \\ u_{xx} = f_{i + 1, j} + f_{i - 1, j} - 2 f_{i, j}; \\ u_{yy} = f_{i, j + 1} + f_{i, j - 1} - 2 f_{i, j}; \\ u_{xy} = \frac{f_{i + 1, j + 1} + f_{i - 1, j - 1} - f_{i + 1, j - 1} - f_{i - 1, j + 1}}{4} 。 \end{matrix} \end{matrix}$

将该离散化格式代入新的算子中对图像进行计算, 从而完成近峰区聚焦评价函数的设计。

1.3 调焦控制策略的设计

根据前文对图像聚焦过程的分析, 调焦控制策略也采用分段式的方法, 选取分段式的调焦策略来完成图像聚焦^[8]。

设置阀值 $\begin{matrix} T_{n}, \end{matrix}$ 根据式(1)计算当前图像的聚焦评价函数值, 当其满足:

$\begin{matrix} | V_{k} - V_{k - 1} |> T_{n} \end{matrix}$ (8)

说明聚焦评价函数位于近峰区, V_k为聚焦评价函数在位置k处的值。首先对当前视域内图像进行识别分割预处理后, 选取锆石目标区域进行计算, 计算V_k和V_k-1的差值, 根据它们的大小来决定聚焦的方向, 同时以小步长l=2 μ m及更小步长驱动电机前进(见图6), 采用爬山法^{[16, 17]}逐步搜寻函数极值点, 最终得到聚焦位置。

当 $\begin{matrix} T_{n} \end{matrix}$ 满足:

$\begin{matrix} | V_{k} - V_{k - 1} |< T_{n} \end{matrix}$ (9)

说明目前正处在远峰区。单纯地以爬山法判断易受到噪声的影响, 所以采用将聚焦评价函数值进行差分累加的方法^[8], 这样的优势在于可以将局部的噪声淹没在一个较大的累积数值中, 有效抑制干扰。

设置阀值 $\begin{matrix} T_{f}, \end{matrix}$ 当满足:

$\begin{matrix} T_{f} > \sum_{1} | V_{k} - V_{k - 1} | \end{matrix}$ (10)

说明聚焦评价函数处在远峰区, 根据 $\begin{matrix} V_{k} 和 V_{k - 1} \end{matrix}$ 的差值判断聚焦方向, 然后以大步长L=20 μ m, 驱动电机前进(见图6), 当计算的评价函数值超过阀值 $\begin{matrix} T_{f}, \end{matrix}$ 代表图像近峰区, 再采用小步长进行聚焦细调。

	Figure Option View Download New Window
	图6 调焦控制策略示意图Fig.6 Schematic diagram of focusing control strategy

2 实验结果与讨论

2.1 聚焦评价函数单峰性、抗噪性对比测试

本实验将对传统聚焦评价函数、局部坐标算子聚焦评价函、李抵非博士基于现有SIMS平台设计的改进型拉普拉斯算子聚焦评价函数^[8]分别进行对比测试, 从而观察其各自函数的单峰性效果。

系统先从模糊的远峰区图像进行采集, 电机采用20 μ m的步进采集图像, 在近峰区图像清晰区电机采用2 μ m的步进采集图像, 最后直到图像再次进入模糊区域。共采集50帧的画面进行计算, 通过采用不同算子的聚焦评价函数进行多次实验进行对比, 图7为几种评价函数的归一化聚焦曲线图。

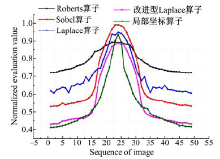	Figure Option View Download New Window
	图7 局部坐标算法与其他算法聚焦评价函数对比图Fig.7 Comparison of various focus evaluation functions: proposed local coordinate algorithm and other algorithms

从图7中可以看出各个评价函数的峰型拥有不同的分布形态和陡缓程度。形状偏“ 陡峭” 的函数拥有更好的聚焦特性。这里采用函数峰度系数来评价函数的分布形态和陡缓程度。评价公式如式(11)所示, 峰度系数是函数四阶中心矩与方差平方的比值。

$\begin{matrix} Kurtosis = \frac{\overset{N}{\sum_{i = 1}} (Y_{i} {- \bar{Y})}^{4}}{(N - 1) S^{4}} \end{matrix}$ (11)

分别以Roberts算子、Sobel算子、Laplace算子、改进型Laplace算子、局部坐标算子为核心的评价函数的峰度系数值为3.67、8.19、3.71、8.45、8.73。可以看出, Roberts、Laplace算子的峰度系数数值上接近3, 形态上接近正态分布, 函数峰值区域较为平坦, 不利于聚焦的实现。Sobel算子、改进型Laplace算子、局部坐标算子峰值系数数值均大于8, 表明这3种算子的函数极值特性更明显。而其中局部坐标算子峰值系数最大, 表明其单峰性最好, 具有明显极值, 具备更优异的聚焦特性。

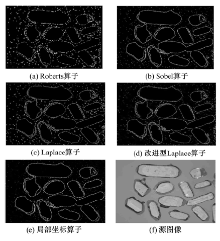
图8为各传统算子、改进型Laplace算子、本局部坐标差分算子对锆石图形的边缘信息保留及对噪声的处理效果。其中图8(e)为局部坐标作为聚焦评价函数时对图像边缘信息的处理效果, 相对于其他算子对原图像的处理(见图8(a)(b)(c)(d)), 其对图像的边缘信息的保留比较完整, 噪声滤除作用明显。

	Figure Option View Download New Window
	图8 局部坐标算子与其他算子对图像边缘处理效果图Fig.8 Edge processing effect by local coordinate operator and other operators

2.2 聚焦准确率测试

聚焦准确度是评价锆石图像自动聚焦系统稳定性的重要指标, 本文将对Roberts算子、Sobel算子、Laplace算子、改进型Laplace算子和局部坐标算子分别作为聚焦评价函数时的聚焦准确度进行实验对比, 步进电机在聚焦轴聚焦坐标进行多次重复采集, 每种算子各进行200次实验, 电机步进为2 μ m。

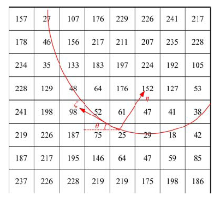
最终采集到的各算子的重复测试位置统计图如图9~图11所示, 从图中可以看出, 各算子重复定位最多的坐标位置是40.536 mm, 即坐标40.536 mm为锆石图像最清晰处, 根据TOF-SIMS仪器的一次离子束斑特性(约5 μ m), 设定在(40.536± 0.004) mm区域为系统的稳定聚焦区域。

	Figure Option View Download New Window
	图9 Roberts、Sobel算子聚焦位置分布图Fig.9 Focusing position of Roberts and Sobel operator

由图9(a)可看出, Roberts算子作为聚焦评价函数时聚焦稳定性较差, 系统聚焦位置分布比较分散, 在200次实验中, 只有74次测试是落在(40.536± 0.004) mm这个系统稳定聚焦区域, 聚焦准确度只有37%。由图9(b)可看出, Sobel算子作为聚焦评价函数时聚焦稳定性相比于Roberts算子有明显的提高, 聚焦区域相对集中, 在200次实验中, 有176次测试是落在(40.536± 0.004) mm这个系统稳定聚焦区域, 聚焦准确度为88%。

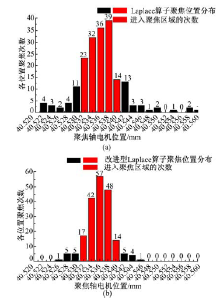
	Figure Option View Download New Window
	图10 Laplace、改进型Laplacel算子聚焦位置分布图Fig.10 Focusing position of Laplace and improved Laplace operator

由图10(a)可以看出, Laplace算子作为聚焦评价函数时聚焦稳定性介于Roberts算子和Sobel算子之间, 但聚焦区域较为分散, 表明抗噪能力较差, 在200次实验中, 有144次测试是落在(40.536± 0.004) mm这个系统稳定聚焦区域, 聚焦准确度为72%。由图10(b)可以看出, 改进型Laplace算子作为聚焦评价函数时聚焦稳定性明显好于传统Laplace算子, 与Sobel算子较为接近, 在200次实验中, 有178次测试是落在(40.536± 0.004) mm这个系统稳定聚焦区域, 聚焦准确度为89%, 但李抵非博士当时设计的此算法的聚焦置信区间为± 0.01 mm^[8], 按照这个标准, 在200次实验中, 聚焦轴电机位置均落在了(40.536± 0.01) mm这个区域, 聚焦准确度达100%。

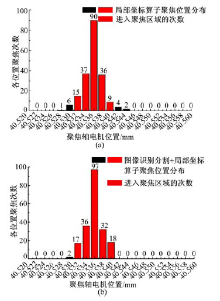	Figure Option View Download New Window
	图11 局部坐标算子聚焦位置分布和图像识别分割后聚焦位置分布图Fig.11 Focusing position of local coordinate operator and position after image captured and segmented

由图11(a)可以看出, 局部坐标算子作为聚焦评价函数时, 在200次实验中有187次测试是落在(40.536± 0.004) mm这个系统稳定聚焦区域, 聚焦准确度高达93.5%。当先采用图像识别分割将锆石图像与背景图像分离后, 再利用局部坐标算子作为聚焦评价函数进行聚焦运算时, 聚焦位置分布图如图11(b)所示, 在200次实验中, 有198次测试是落在(40.536± 0.004) mm这个系统稳定聚焦区域, 聚焦准确度为99%, 表明这种算法消除噪声的能力较强, 有更稳定的聚焦准确度。

3 结束语

本文提出一种具有自动消除噪声功能的锆石样品图像自动聚焦算法, 该算法包括锆石图像识别分割法, 分段式聚焦算法和调焦控制策略。将本文算法应用于TOF-SIMS仪器后, 系统聚焦准确率可达99%, 可有效抑制噪声干扰, 保证了聚焦准确度。本文算法可以为同类仪器自动聚焦系统的设计提供一定参考。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	James K, Lee W, Williams I S. Pb U and Th diffusion in nature zircon[J]. Nature, 1997, 390(13): 159-162. [本文引用:1]
[2]	Cherniak D J, Watson E B. Pb diffusion in zircon[J]. Chemical Geology, 2000, 172(1/2): 5-24. [本文引用:1]
[3]	Compston W, Williams I S, Kirschvink J L, et al. Zircon U-Pb ages for the Early Cambrian time-scale[J]. Journal of the Geological Society, 1992, 149: 171-184. [本文引用:1]
[4]	Foster J J. The construction and development of SHRIMP I: an historical outline[J]. Precambrian Research, 2010, 183(1): 1-8. [本文引用:1]
[5]	王培智, 田地, 包泽民, 等. TOF-SIMS样品光学成像系统设计[J]. 质谱学报, 2015, 36(3): 282-288. Wang Pei-zhi, Tian Di, Bao Ze-min, et al. Design of TOF-SIMS's sample optical imaging system[J]. Journal of Chinese Mass Spectrometry Society, 2015, 36(3): 282-288. [本文引用:1]
[6]	Zhao Q, Liu B, Xu Z. Research and realization of an anti-noise auto-focusing algorithm[C]//IEEE 5th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), Hangzhou, China, 2013: 26-27. [本文引用:1]
[7]	Yin P, Jiang W. Autofocusing region selection for computer vision[C]//IEEE 9th International Conference on Signal Processing, Beijing, China, 2008: 26-29. [本文引用:1]
[8]	李抵非. 基于分段式策略的图像自动聚焦研究[D]. 吉林大学: 仪器科学与电气工程学院, 2012. Li Di-fei. The study on image auto-focus system with segmented strategy[D]. Changchun: College of Instrumentation and Electrical Engineering, Jilin University, 2012. [本文引用:8]
[9]	Jiang Tian-zi, Yang Fa-guo. An evolutionary tabu search for cell image segmentation[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics Archive, 2002, 32(5): 675-678. [本文引用:1]
[10]	Simon I, Pound C R. Automated image analysis system for detecting boundaries of live prostate cancer cells[J]. Cytometry, 1998, 31(4): 287-294. [本文引用:1]
[11]	Pertuz S, Puig D, Garcia M A. Analysis of focus measure operators for shape-from-focus[J]. Pattern Recognition, 2013, 46(5): 1415-1432. [本文引用:1]
[12]	Muhammad M S, Choi T S. Sampling for shape from focus in optical microscopy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(3): 564-573. [本文引用:1]
[13]	Muhammad M S, Choi T S. Nonlinear approach for enhancement of image focus volume in shape from focus[J]. IEEE Transactions on Image Processing, 2013, 21(5): 2866-2873. [本文引用:1]
[14]	Song B. Topics in variational PDE image segmentation inpainting and denoising[D]. Los Angeles: University of California Los Angeles, 2003. [本文引用:1]
[15]	Zhang H Y, Peng Q C. Adaptive image denoising model based on total variation[J]. Opto-Electronic Engineering, 2006, 33(3): 50-53. [本文引用:1]
[16]	Wang Z X, Chen Z T, Zhao Ya, et al. A novel local maximum potential point search algorithm for topology potential field[J]. International Journal of Hybrid Information Technology, 2014, 7(2): 1-8. [本文引用:1]
[17]	He L, Zhou R Z, Hong Z. Modified fast climbing search auto-focus algorithm with adaptive step size searching technique for digital camera[J]. IEEE Transactions on Consumer Electronics, 2003, 49(2): 257-262. [本文引用:1]

1997

0.0

... 0 引言锆石U-Pb定年是同位素年代学研究中最常用和有效的方法之一^[1,2] ...

2000

0.0

... 0 引言锆石U-Pb定年是同位素年代学研究中最常用和有效的方法之一^[1,2] ...

1992

0.0

... 二次离子质谱仪(Secondary ion mass spectrometer,SIMS)作为高分辨、高精度的表面分析仪器,可以在锆石样品上数微米的范围内获取精确的同位素及化学组成信息,是一种无需对样品进行化学处理和近于无损伤的分析技术,非常适用于变质增生壳厚度只有数微米的锆石样品的微区原位分析^[3,4,5] ...

2010

0.0

2015

0.0

. 2015, 36(3):282-288 DOI:doi:10.7538/zpxb.youxian.2015.0005

Design of TOF-SIMS's sample optical imaging system

TOF-SIMS样品光学成像系统设计

Wang Pei-zhi , Tian Di , Bao Ze-min

王培智, 田地, 包泽民

A high spatial resolution sample optical imaging system for the time of flight-secondary ion mass spectrometer （TOF-SIMS） was designed. The system consists of an improved Schwarzschild double reflection system, a reflector lens of 45°, a zoom lens and a CCD image sensor. The ZEMAX software was used to calculate and improve the initial Schwarzschild model and give the parameters of improved system. The simulation results show that the best imaging resolution of the system can reach 1 μm, the maximum resolution can achieve to 0.4 μm, and the RMS radius is less than airy disk diameter. The wave aberration can satisfy the Rayleigh judgment, and the image quality shows well.

本研究为飞行时间二次离子质谱仪（TOF-SIMS）设计了一种具有高空间分辨率的样品光学成像系统。该系统由一种改进的Schwarzschild双反射系统、45°反射镜、变焦镜头及CCD图像传感器构成。采用ZEMAX软件对传统Schwarzschild模型进行计算和改进，得出系统优化参数并进行仿真验证。仿真结果表明：系统最佳的成像分辨率达1 μm，极限分辨率为0.4 μm，RMS半径小于艾里斑直径，波像差满足瑞利判据，成像质量良好。

2013

0.0

... 锆石样品图像的噪声来源主要有CCD相机产生的电噪声、样品靶表面不平整产生的图像噪声等,这些噪声均会影响自动聚焦系统运行时的准确度^[6] ...

2008

0.0

... 以传统图像边缘检测算子为核心的自动聚焦算法无法有效地抑制噪声干扰^[7],这些干扰会导致图像聚焦位置不准确,聚焦位置不准确会造成SIMS仪器的一次离子束实际轰击点与图像显示点存在位置偏移,影响仪器采集数据的准确性 ...

2012

0.0

. 2012, :-

The study on image auto-focus system with segmented strategy

基于分段式策略的图像自动聚焦研究[D]

Li Di-fei.

李抵非

本论文依托于中国地质科学院“十一五”国家科技支撑计划重点项目“二次离子质谱仪器核心技术及关键部件研究与开发”。针对二次离子质谱仪中图像聚焦系统对高精度和高抗干扰能力的需求，本文设计了相应的软硬件系统，在该项技术方面做出了相关研究并切实应用。自动聚焦系统关键技术组成则包含两部分：聚焦评价函数和调焦控制策略。聚焦评价函数是在整个聚焦过程中计算当前图像的清晰度，从而确定图像是否聚焦；调焦控制策略是控制镜头移动搜索聚焦点的手段，它是根据当前聚焦评价函数的计算值来确定移动相机镜头的移动方向和移动幅度。所以聚焦系统的这两部分技术是紧密结合的。本文即是对以上这两方面技术在提高精确性以及抗干扰性方面进行研究与改进，提出了一种数字图像的分段式聚焦策略。将整个聚焦过程分为两个阶段，在远离聚焦点时，采用灰度差分绝对值聚焦函数以及差分累加的调焦控制策略进行粗调，加速聚焦的速度；在接近聚焦点附近时，利用改进的经过改进拉普拉斯聚焦评价函数与两点方向判断法相结合进行聚焦细调；同时采用图像分割法，捕捉图像中的目标部分，减少无用的背景像素对运算效率的影响；引入遗传算法对传统聚焦评价函数进行修正，使其可随环境变化调整参数，使整个系统适应外部条件的变化，提高聚焦精确度。该方法提高自动聚焦系统的精确度，增强了自动聚焦系统的抗干扰性，适用于在精确度要求较高和外部干扰较强的聚焦场合的应用。

... 李抵非博士^[8]在2012年基于原有SIMS仪器平台,提出一种以改进的拉普拉斯(Laplace)算子为核心的具有抗干扰能力的自动聚焦算法,实现了锆石图像的准确聚焦 ...

... 如图3所示^[8],图像处于远峰区时,函数的斜率较小,代表聚焦评价函数值的变化较为缓慢 ...

... 若设置一适当的阈值 T将聚焦评价函数合理地分为两段,在远峰区采用运算速度较快的算子,在近峰区采用抗噪性较强的算子,就可以发挥不同算子的优势,取得更好的效果^[8] ...

... 在进入聚焦评价函数近峰区时,传统的灰度梯度算子无法有效识别图像边缘并且不能去除灰度变化缓慢区域内的大梯度噪声,李抵非博士^[8]设计的改进型Laplace算子虽能在一定程度上抑制噪声干扰,但其应用背景是一次离子束斑直径为20~30 #cod#x003bc ...

... 3 调焦控制策略的设计根据前文对图像聚焦过程的分析,调焦控制策略也采用分段式的方法,选取分段式的调焦策略来完成图像聚焦^[8] ...

... 单纯地以爬山法判断易受到噪声的影响,所以采用将聚焦评价函数值进行差分累加的方法^[8],这样的优势在于可以将局部的噪声淹没在一个较大的累积数值中,有效抑制干扰 ...

... 1 聚焦评价函数单峰性、抗噪性对比测试本实验将对传统聚焦评价函数、局部坐标算子聚焦评价函、李抵非博士基于现有SIMS平台设计的改进型拉普拉斯算子聚焦评价函数^[8]分别进行对比测试,从而观察其各自函数的单峰性效果 ...

... 01 mm^[8],按照这个标准,在200次实验中,聚焦轴电机位置均落在了(40 ...

2002

0.0

... 本文所设计的这种图像分割方式适合于具有封闭边缘特性的目标图像,如生物领域的细胞分割图像学^[9,10]等 ...

1998

0.0

... 本文所设计的这种图像分割方式适合于具有封闭边缘特性的目标图像,如生物领域的细胞分割图像学^[9,10]等 ...

2013

0.0

... 目前的聚焦评价函数多采用灰度梯度法^[11,12,13] ...

2012

0.0

... 目前的聚焦评价函数多采用灰度梯度法^[11,12,13] ...

2013

0.0

... 目前的聚焦评价函数多采用灰度梯度法^[11,12,13] ...

2003

0.0

... 鉴于此,作者采用了一种基于局部坐标二次微分^[14,15]的边缘检测算子,使得上述问题得以有效的解决 ...

2006

0.0

... 鉴于此,作者采用了一种基于局部坐标二次微分^[14,15]的边缘检测算子,使得上述问题得以有效的解决 ...

2014

0.0

... m及更小步长驱动电机前进(见图6),采用爬山法^[16,17]逐步搜寻函数极值点,最终得到聚焦位置 ...

2003

0.0

... m及更小步长驱动电机前进(见图6),采用爬山法^[16,17]逐步搜寻函数极值点,最终得到聚焦位置 ...