作者简介:刘海鸥(1975-),女,副教授,博士.研究方向:车辆传动与控制.E-mail:bit_lho@bit.edu.cn
为了满足履带车辆传动系统动态载荷谱编制对采集数据准确性的要求,运用功率谱分析方法获取原始采集载荷谱信号的频率分布,确定了有效信号的频域特性。利用小波分析方法,给出了在通用阈值基础上改进的自适应阈值去噪的计算方法。结合实车动态行驶与换挡过程中的传动特性对实测履带车辆载荷谱信号去噪结果进行了分析。研究结果表明:改进的自适应阈值去噪方法能更好地区分不同频段上的有效信号和噪声信号,在保留中、高频载荷谱信号的前提下具有良好的去噪效果。
In order to satisfy accuracy requirement of testing data for the compiling of dynamic load spectrum of tracked vehicle transmission, the problem of how to deal with the irregular noise, usually existing in the dynamic load spectrum signal, was studied. First, the collected signal is analyzed by power spectrum analysis. The frequency distribution and the characteristics of the load signal were briefly analyzed, and the main distribution range of the useful signal was determined. Then, the wavelet analysis method for dynamic load spectrum signal de-noising was studied, and the calculation method of adaptive threshold developed from universal threshold was presented. Quantificational evaluation based on SNR and MSE, the de-nosing results of typical sine simulation signal with different noise pollution indexes were comparatively analyzed, and the de-noising results of load simulation signal with real noise signal were also comparatively analyzed both using the two methods. Furthermore, combined with the real transmission characteristics in the process of dynamic driving and gear shifting, effective analysis was presented. It shows that the adaptive threshold de-noising method has a better de-noising effect on the premise of keeping useful medium-high frequency dynamic load spectrum signal.
履带车辆传动系统动态载荷谱是对其零部件疲劳寿命进行估计和可靠性分析的基础[1], 与静态低频载荷谱的区别在于需要尽可能多地保留测试中所采集的动态中高频载荷信号。然而, 在测试过程中混杂的噪声信号也大多属于中高频信号。因此, 本文在尽量保留动态载荷谱中高频有效信号的前提下进行去噪研究。
基于小波分析的通用阈值去噪方法最早由Donoho[2]提出, 随后Berkner等[3]学者提出了分层阈值的理论与方法, 并且广泛应用于各领域, 例如在记录地震信号时进行去噪、图像处理、心电图分析等[4, 5, 6]。很多学者针对具体的问题对其应用也做了一些改进, Liu等[6]提出在心电图信号处理中根据不同的分解层数使用不同的阈值; Zhang等[7]提出半软双阈值优化的方法用于激光信号处理; Hemant等[8]提出ABC算法用于一维信号降噪, 取得了良好的效果。
由于通用阈值去噪方法中的噪声方差是根据最精细分解层小波系数估计的, 在履带车辆动态载荷谱信号去噪研究中发现, 该方法计算出的通用阈值会过多地去掉有效动态载荷信号。本文基于对小波去噪理论的研究, 在通用阈值去噪方法的基础上提出了基于噪声分析的噪声方差估计方法, 进一步得到了适用于载荷谱信号去噪的自适应阈值计算方法, 并且通过两种仿真信号的处理结果进行验证; 同时, 结合车辆动态传动特性, 进一步分析了去噪结果的合理性。
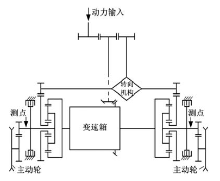
本文研究的履带车辆传动装置组成和基本布置如图1所示。为了测试传动系统载荷谱信号, 采用了基于应变式扭矩测试原理的测试系统以及德国IMC公司的智能模块数据采集系统, 采集的信号有:变速箱左右输出轴扭矩和转速、换挡信号、操纵系统油压、车速等, 变速箱输出轴测点如图1中测点(以下选取左侧输出扭矩进行分析), 使用快速信号分析处理软件FAMOS读取所测试的数据。
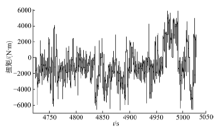
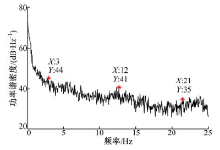
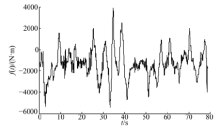
以履带车辆变速箱输出轴所受载荷为例, 对其动态载荷特性进行分析。图2为某履带车辆在起伏路上行驶5 min的实测载荷信号, 对其进行功率谱分析[9], 如图3所示。可以看出, 载荷信号的频率主要分布在0~21 Hz, 而以0~3 Hz最为集中。
履带车辆由于行驶工况复杂和用途特殊, 其传动系统所承受的载荷多属随机附加载荷。例如, 越障之前在较平坦的路面上行驶时, 来自道路的激励大多属于较平稳载荷信号, 主要集中在低频段(0~3 Hz); 在越过起伏坡道时产生的冲击以及传动系统由于扭振作用和换挡冲击而产生的载荷信号主要集中在中高频段(3~21 Hz)。所以, 履带车辆传动系统的动态载荷信号在低、中、高各频率段均有分布[10]。
与基于光学、磁学等其他测试方法相比, 本文采用的基于应变法的测试系统具有更好的稳定性, 更加适用于复杂的测试环境, 故能够保证采集到的载荷信号具有较高的信噪比。但是在车辆动态载荷谱信号数据采集过程中, 由于受到温度等外界环境干扰以及其他车载用电设备对测试电路的电磁干扰, 使得有用载荷信号中混杂了噪声, 信噪比降低, 该噪声主要是各种频率的杂波信号等。
小波分析方法能同时在时频域中对信号进行处理, 并能有效地区分所采集载荷谱信号中的有效部分和噪声部分, 从而实现信号的去噪。
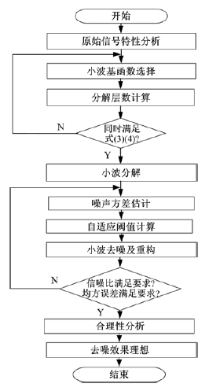
小波分析是通过伸缩(膨胀)和平移等运算功能对载荷信号进行多尺度化分析, 是比较理想的对信号进行局部频谱分析的数学工具, 其去噪过程如图4所示。
在实际信号处理中, 通常使用如下二进离散小波序列[11]:
式中:ψ j, k (t)为小波序列; ψ (t)为基小波; j为分解层数, k为平移参数, j, k∈ Z。
信号
最优小波基函数的选用是小波分析应用到实际中的一个难点问题, 目前往往是通过经验或不断试验对比来选择[12]。此种方法虽然繁琐却有效, 尤其在对信号特性不完全了解的情况下, 本文首先将与原始信号趋势相近的小波基函数, 例如dBN小波、symN小波、CoifN小波等, 与所要处理的载荷谱信号的特征进行对比, 选用了与其趋势最相近的dBN小波基函数, 其特点是紧支正交基, 满足精确重建条件。
离散小波变换的分解层数在各个领域应用都是一个基本问题, 目前还没有明确的解决方法。本文提出采用“ 信号需要被处理的最小频率应该大于或等于小波分析最大尺度
式中:fc为小波基函数对应的中心频率; Δ t为采样周期; minfsignal为信号需要被处理的最小频率。
离散小波变换的分解层数是对尺度进行二进离散采样。因此, L对应的分解层数j可由下式来确定, 即:
式中:
目前, Donoho[2]所提出的小波分析通用阈值去噪和Berkner等[3]所提出的分层阈值去噪的方法被广泛应用于信号预处理中, 但大多数研究中噪声方差
各分解层上应取阈值为:
式(5)(6)中:σ 为噪声标准方差; ω 1, k为待处理信号最精细层小波系数; median(· )为取中值; λ 为通用阈值; N为信号长度。
本文通过大量试验发现, 在对履带车辆动态载荷谱信号进行去噪处理时, 采用以上两种通用方法估计出来的噪声方差偏大, 导致各分解层阈值计算偏大, 过多地去除了有用中高频动态载荷信号。因此, 本文提出了基于噪声信号分析的噪声方差估计方法, 以得到各分解层自适应阈值, 如式(7)(8)(9)所示:
式中:
为了精确地反映去噪效果, 通常使用信噪比和均方误差来描述[14]。原始不含噪声的真值信号为x(t), 经过小波去噪后的信号为
式中:
原始不含噪声信号x(t)与小波去噪信号
式中:MSE为均方误差。
为了分析本文提出的自适应阈值去噪方法的效果, 首先对不同频率、不同信噪比的正弦仿真信号进行去噪分析。为了使仿真信号更接近实测载荷信号, 取频率分别为5 Hz、15 Hz和25 Hz的正弦信号代表载荷信号的低、中、高频段; 对实测载荷信号分析可知其信噪比可能在10~30 dB区间, 在此可取10、16、22和29 dB四种信噪比作为噪声污染指标。
本文是通过在不同频率的正弦信号中加入不同强度的白噪声来构造仿真信号。以基波为25 Hz具有4种信噪比的正弦仿真信号为例, 各组信号通过两种方法去噪后计算的信噪比和均方差如表1所示。再以信噪比为16 dB的3种频率的正弦信号为例进行去噪分析, 结果如表2所示。
| 表1 不同噪声污染指标的去噪结果对比 Table 1 De-noising results of different noise pollution index |
| 表2 不同频率原始信号去噪结果对比 Table 2 De-noising results of different frequencies |
根据经验, 信噪比越高, 均方误差越小, 则去噪信号越接近原始真值信号, 去噪质量越高[15]。可以看出, 两种方法去噪之后信噪比都得到了提高, 并且本文方法去噪效果更加明显。
3.2.1 载荷仿真信号的构造
由于试验所采集的动态载荷谱信号很难获得其理论值, 不利于对去噪效果进行评价, 在此需要构造一个真值已知叠加噪声的载荷信号
式中:s(t)为不含噪声的真值信号; n(t)为噪声信号。
真值信号
车况良好, 在水平路面上, 发动机启动, 测试设备打开, 开始采集噪声信号, 怠速80 s后, 发动机熄火并保存数据。一段时间(约30 s)后发动机再次启动, 依此重复进行11次采集, 将11次采集到的噪声按照其信号强度从小到大的顺序排列, 取第6次(中值)得到的噪声数据[16], 如图5所示。
含有噪声的载荷仿真信号
3.2.2 载荷仿真信号去噪结果分析
首先, 在dBN系列小波基函数中, 选用工程中经常使用的dB4小波进行处理, 借鉴图3所示的频率信息, 载荷信号
计算得L≥ 11.905, 取整数得L=12, 则小波分解层数j=4。
根据式(1)(2)(5)(6)计算出各分解层上应取的噪声方差估计值σ , 再计算出通用阈值λ , 选用软阈值函数, 计算结果如表3所示。
| 表3 通用阈值λ Table 3 Universal threshold λ |
根据式(1)(2)(7)(8)(9)计算出各分解层上应取的噪声方差估计值σ j, 再计算出各分解层的自适应阈值λ j, 选用软阈值函数, 计算结果如表4所示。可以看出, λ j随着分解层数增大, 呈现出逐渐减小的规律。
| 表4 自适应阈值λ j Table 4 Adaptive threshold λ j |
两种方法的去噪结果对比如图7所示。两种方法去噪之后的信噪比(SNR)和均方差(MSE)对比如表5所示。
| 表5 信噪比和均方差 Table 5 SNR and MSE |
容易看出, 相比被处理前, 经过两种方法去噪后其信噪比都有了提高; 对比通用阈值去噪方法, 本文方法其信噪比有了明显提高, 均方差有了明显减小, 这说明去噪之后的信号更加接近原始真值信号。进一步分析可知, 相对于通用阈值方法, 本文方法在较高频层(第1、2层)具有更大的阈值, 也就是可以去掉更多的噪声; 在较低频层(第3、4层)具有相对小的阈值, 也就是可以保留更多的有效信号。由此, 可以看出本文提出的噪声方差估计和自适应阈值方法更适用于履带车辆动态载荷谱信号的去噪, 并能更好地保留有效动态载荷。
最后, 运用本文方法对dBN系列不同的小波去噪能力做对比实验, 以选出最优小波基函数, 评价指标为SNR和MSE, 如表6所示。
| 表6 最优小波基函数评价 Table 6 Evaluation of optimal wavelet basis |
由表6可以看出dB4小波基函数的去噪结果具有更高的信噪比和更小的均方差, 故适用于履带车辆传动系统载荷谱信号去噪。
3.3.1 实测载荷信号去噪结果
采用本文方法对履带车辆随机行驶工况下实测的动态载荷谱信号(见图2)进行去噪处理, 选择dB4小波, 分解层数为4; 再计算各个分解层的自适应阈值, 选用软阈值函数。自适应阈值去噪结果与实测信号对比如图8所示。
3.3.2 实测载荷信号去噪结果分析
与载荷仿真信号不同的是, 目前实测载荷信号的真值信号无法获得, 因而不能通过信噪比和均方差评价去噪结果, 针对这种情况, 本文提出了基于车辆传动特性的分析评价方法。
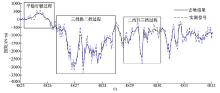
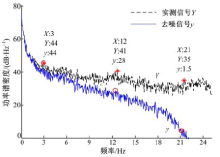
由图8可以看出, 自适应阈值去噪结果能保留与实测信号相近的波动趋势。再将二者的功率谱图进行对比, 如图9所示, 可以看出低频段0~3 Hz的幅值没有变化, 能完全保留低频动态载荷信号; 中频段3~12 Hz的幅值较实测信号有所降低, 即去掉了此频段的噪声保留了大部分有效载荷; 同时高频段12~21 Hz的频率信息也有所保留, 即保留了有效高频载荷, 还可以看出21 Hz以上的频率信息(在此认为是噪声信号)不存在, 与实际要求相符。
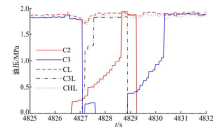
基于履带车辆的动态传动特性再对去噪结果做进一步分析。在此引入车辆行进过程中的换挡逻辑和各执行元件油压变化图, 如表7和图10所示。同时参照图8, 在4826 s以前, 挡位无变化, 车辆平稳行驶, 此时变速箱输出扭矩变化平缓, 载荷波动较小; 在4826~4831 s区间车辆经历了从三挡降二挡和二挡升三挡两个过程, 可以看出, 变速箱输出扭矩变化剧烈, 载荷波动较大, 符合换挡过程中的动态载荷变化情况。经此分析可知, 本文的自适应阈值去噪方法是在保留有效中、高频载荷信号的前提下进行去噪, 满足履带车辆传动系统动态载荷谱信号的去噪要求。
| 表7 挡位与执行元件关系图(部分) Table 7 Relationship between gears and actuators |
(1)本文在传统小波通用阈值去噪方法的基础上, 提出了适用于履带车辆传动系统动态载荷谱信号去噪的小波基函数、分解层数、噪声方差和自适应阈值等参数的选择和计算方法。
(2)分别对通用方法和本文方法的仿真信号去噪结果进行对比, 验证了本文方法具有更为准确、合理的去噪效果。
(3)将本文方法用于实测动态载荷谱信号去噪, 通过对其结果的合理性分析可知去噪结果更接近于履带车辆传动系统实际工作中所受到的动态载荷, 这也为后期动态载荷谱的编制提供了更加有效、可靠的数据。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|