基于汽车碰撞仿真结果进行车身安全性设计和改进已经被广泛应用^{[1, 2, 3]}。上世纪30年代, 国外已经开始利用汽车实车碰撞试验来检测和优化汽车安全性, 但这种方式存在很多缺点, 比如试验费用高、汽车样车制作困难、后期优化改进费用较高以及部分碰撞试验信息采集困难等^[4]。如今, 汽车碰撞数值模拟已经被广泛采用, 比如ESI公司在CRAY1计算机上使用PAMCRASH数值模拟汽车碰撞^{[5, 6]}。

目前, 汽车碰撞数值模拟主要有三种:机械振动学法、多体系统动力学法和有限元法。多体系统动力学法是建立多体动力学方程, 其优点是模型简单、编程难度小、计算速度快^{[7, 8]}。机械振动学法是基于质量点弹簧模型依据汽车碰撞各个质量点的位移情况, 将汽车各个主要部件离散为一个弹簧-质量点振动系统, 测定系统中弹性元件的力学特性后利用振动方程计算的方法求解碰撞系统运动学特性的方法, 优点是程序简明、能够比较真实地反应变形体的弹塑性变形特性。有限元法就是将整个汽车实体结构分解为离散的有限元单元体, 通过专业的碰撞分析软件模拟变形和运动过程, 其优点是方法专业、适用范围广、数据全面^{[3, 4]}。

在概念车开发初期, 整车材料、形状和尺寸均未确定。在概念设计阶段对整车安全性能进行数值模拟, 在上述三种碰撞分析方法之中, 使用机械振动方程对安全性能进行定性计算是比较可行的^{[9, 10]}。其计算结果可以指导结构设计工程师合理地布局主要部件和它们的连接方式。

因此, 本文采用了机械振动学法。模型中, 各部件质量为定值, 初始主要部件之间的刚度曲线根据经验设定, 主要部件位置为不确定值, 安全指标为待求量, 例如车身和动力总成的加速度峰值, 因此它们也是本文的优化目标。优化参数就是主要部件的布局位置坐标。

在这个模型上, 本文采用了改进的牛顿下山法作为多目标优化方法。迭代中, 使用Wilson-θ 法加强计算的稳定性。每次求解的振动方程中的刚度阵都是由刚度曲线上对应的点组装的总刚度阵, 保证了计算的可靠性。

最后, 通过一个概念车模型主要部件布局优化例子证明了本文方法的可行性。

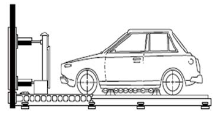
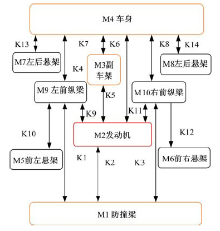
整车设计开发流程包括5个阶段:方案策划阶段、概念设计阶段、工程设计阶段、样车试验阶段、投产启动阶段^[7]。在概念设计阶段根据整车性能的设计目标确定汽车总布置方案。进一步的, 在概念设计阶段从碰撞安全角度考虑, 本文将汽车碰撞简化成为一个弹簧质量的机械振动系统。整车碰撞模型如图1所示, 力学特性如图2所示, 忽略其他小质量部件。该系统由动力总成、副车架、车身、左(右)前纵梁, 左(右)前悬架及轮胎, 左(右)后悬架及轮胎等部件, 以及它们的弹性关系组成的质量弹簧系统。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 汽车碰撞静态模型Fig.1 Static model of automobile collision

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 概念汽车简化模型Fig.2 Simplified model of concept auto

在概念设计阶段, 整车结构没有具体尺寸和材料属性的定义。

但是, 碰撞计算需要一些具体的数值。主要需要的参数就是图2中所有标注的参数。

为了能够在概念设计阶段近似地评价整车的碰撞性能。工程上, 一般根据工程经验和现有成熟整车模型的数据匹配概念车。比如发动机、副车架、车身等主要部件的质量可以根据未来设计目标或已有的车布置质量进行近似匹配, 其安装位置同样匹配并作为设计参数, 即优化变量。

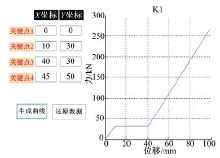
各个部件连接按照弹性连接处理, 如图3所示, 其弹性连接力用刚度曲线表示。而刚度曲线就是由几个关键点确定的简化折线。例如, 图3中左侧为部件连接刚度曲线关键点坐标, 人为输入后在右侧生成刚度折线。每个部件连接都有相类似的弹性折线。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 设计的副车架力-位移曲线及关键点Fig.3 Given force vs. displacement curve and key points of subframe

在这里, 图3是表示概念车每个部件连接关系的等效刚度。碰撞计算中, 这些部件的连接关系是确定的, 也就是力的转递顺序是确定。但是, 力数值的传递和连接部件间的结构和材料直接相关。以前, 工程上习惯于先确定结构和材料再确定计算刚度。概念车的被动安全设计则是相反的。它的设计思想是先给定刚度, 以后在工程设计阶段设计满足刚度要求的结构和材料, 这种设计方法已经被广泛采用。本文提出的刚度的简化折线则是根据被动安全设计部门提供的已有车型的实际刚度曲线, 经过测量后简化得到的。得到的简化曲线如图3所示。算例中的刚度数值同理得到。

每条刚度简化折线总共有4个关键点顺序连接而成。如图3所示, 就是一个关键点曲线输入的程序实例。同理, 本文算例中每条刚度曲线都可以这样输入。

在计算过程中, 根据这种刚度曲线, 插值得到该位置对应的弹性力。

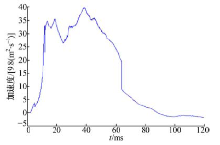
已知某概念车的主要部件及布置简化模型(见图3)。概念车进行仿真碰撞试验时间为120 ms, 时速为50 km/h, 主要部件距保险杠的初始设计距离和部件质量如表1所示。各个主要部件的连接力用图2中的关键点表示, 具体关键点数值如表2所示, 优化前发动机加速度如图5所示, 车身加速度如图6所示。

表1

Table 1

表1(Table 1)

表1 主要部件的质量和初始设计位置 Table 1 Mass and initial layout of key parts 部件名称 部件质量 /kg 部件到保险杠 距离/mm 优化后的 距离/mm 防撞梁 5 21 21 发动机 285 395 320 副车架 962 962 911 车身 1316 2467 2397 左前悬架 72 915 908 右前悬架 72 915 908 左后悬架 56 3457 3457 右后悬架 56 3457 3457 左前纵梁 7 285 274 右前纵梁 7 285 274

表1 主要部件的质量和初始设计位置 Table 1 Mass and initial layout of key parts

表2

Table 2

表2(Table 2)

表2 刚度折线关键点的坐标 Table 2 Key points’ coordinate of stiffness curves 关键点1 关键点2 关键点3 关键点4 K1, K3 11, 144 000 40, 147 000 90, 103 000 99, 105 000 K2 0, 0 0, 0 264, 61 000 291, 158 000 K4, K8 15, 148 000 46, 107 000 149, 103 000 155, 134 000 K5 0, 0 1.5, 133 000 1.78, 122 000 3.57, 156 000 K6 0, 0 -4.67, 16 200 55, 28 600 122, 52 100 K7 51.1, 460 246, 37 500 420, 101 000 440, 146 000 K9 47.6, 0 88, 1060 131.7, 539 136.8, 15 600 K10, K12 K13, K14 2.05, 129 000 4.94, 87 500 20.7, 99 500 22.8, 131 000

表2 刚度折线关键点的坐标 Table 2 Key points’ coordinate of stiffness curves

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 优化前发动机加速度曲线Fig.5 Engine acceleration curve beforer optimization

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 优化前的车身加速度曲线Fig.6 Car body acceleration curve before optimization

设计参数:表2中所有部件的位置参数。

设计目标:①发动机加速度峰值a_发动机≤ 80 g(g=9.8 m²/s); ②车身的加速度峰值a_车身≤ 40 g, 如式(7)(8)所示。

a发动机=f1(d1, d2, d3, …, d9, d10)(7)

a车身=f2(d1, d2, d3, …, d9, d10)(8)

式中: d₁, d₂, …, d₁₀ 为主要部件的位置参数, 即优化参数; f₁ 、f₂分别代表发动机加速度和车身B柱加速度峰值函数, 由于函数无法显式表示, 所以这里大致描述为 f1、f2两个函数。

根据2.1节的优化步骤得到车身加速度曲线, 如图7所示; 发动机加速度曲线如图8所示, 优化后的主要部件的布局参数如表1最后一列所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 优化后的车身加速度曲线Fig.7 Car body acceleration curve after optimization

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 优化后发动机加速度曲线Fig.8 Engine acceleration curve after optimization

从得到的优化曲线的极大值点上看, 图7和图8中的最大值, 即车身的加速度峰值和发动机的加速度峰值分别由优化前的131 g、46 g降到79.2 g、39.9 g, 均达到两个优化目标, 而得到的优化参数值, 即表1中最后一列, 可以用在汽车详细设计阶段作为主要部件布置的依据。

本文在汽车概念设计阶段, 使用多目标优化方法结合汽车碰撞简化模型进行主要部件的布局优化, 使得在这一阶段进行被动安全设计成为可能。得到的主要部件布局, 可以指导汽车结构详细设计。采用该方法优化了某概念车模型的车身和发动机加速度峰值, 结果证明了本文方法的可行性。