车辆在高速行驶时通常会出现车辆失稳现象, 这个现象可能是由于发动机制动引起的, 但是缺乏相关的理论研究和分析^{[1, 2]}。目前关于发动机制动的研究主要集中在如何提高制动效能和建立发动机制动模型方面。

卢从娟^[3]利用发动机制动力进行车速控制, 从而使汽车下坡时的速度保持在安全范围内。颜胜^[4]指出使用发动机制动最大优点是在不使用行车制动装置的情况下, 最大限度控制车速, 并仿真得到了发动机制动力矩与发动机转速之间的关系曲线。此外, Hamersma等^[5]在研究纵向车辆动力学控制时, 得到发动机制动力矩与转速的关系表达式, 但只能表达一种型号的发动机制动力矩特性, 且无法获得发动机转速较低时的发动机制动力矩。

目前, 在车辆模型建立方面, 以二自由度汽车动力学模型为基础的汽车转向稳定性研究已经取得了较丰硕的研究成果^{[6, 7]}。刘丽^[8]通过引入纵向速度的三自由度模型, 揭示了汽车操纵稳定性的本质特征是非线性动力学系统的混沌运动。Wang等^[9]在三自由度模型的基础上, 引入驱动建立的五自由度模型, 揭示了驱动对汽车操纵稳定性的影响。但是缺乏在发动机制动工况下, 发动机制动对车辆系统动力学影响的深入研究。

本文在推导了适用于不同发动机型号和不同转速的发动机制动力矩表达式的基础上, 针对一种型号发动机拟合得到在不同转速下发动机制动力矩的解析表达式, 建立发动机制动工况下的车辆系统五自由度非线性方程。在有、无发动机制动条件下, 通过相空间轨迹、状态变量时间序列、庞加莱截面和功率谱密度等方法, 分析了车辆系统的动力学特性。

根据汽车理论^[10]中发动机的制动力矩表达及相关的经验公式^[11]可得到发动机转速高于怠速(n=800 r/min)条件下, 发动机制动力矩T_e的表达式:

Te=77.928(0.0062+0.0016pmax+0.00003n)Ve(1)

式中:p_max为最高爆发压力; n为发动机转速; V_e为发动机的排量。

根据操纵动力学中车辆系统的运动方程^[12]可知, 车辆高速转向行驶时, 其侧向速度和横摆角速度的耦合作用会对车辆的纵向运动产生影响。当侧向速度和横摆角速度对应的符号相异时, 在耦合作用下, 车辆的纵向加速度逐渐减小, 当驱动力矩为0时, 车辆的纵向速度可能出现负值, 即汽车向后运动, 车轮反转。为揭示驱动轮由正转变为反转过程中车辆的动力学行为及车辆的稳定性, 研究并获得n∈ [0 800] r/min时发动机转矩与转速之间的解析表达式十分必要。为得到发动机转速n≥ 0过程中发动机制动力矩的完整表达, 在发动机转速n∈ [0 800] r/min时假设发动机制动力矩与转速之间为线性关系, 采用线性拟合的方法得到该转速范围内发动机制动力矩的计算公式为:

Te=77.928(0.0302+0.0016pmax)Ve800n(2)

由此得到发动机制动力矩的完整表达式为:

Te=77.928(0.0062+0.0016pmax+ 0.00003n)Ve (n≥800r/min)77.928(0.0302+0.0016pmax)Ve800n (0≤n< 800r/min)(3)

由于发动机制动力矩经变速器及主减速器传递到驱动轮上, 根据发动机转速与驱动轮转速之间的关系, 可计算得到作用于驱动轮的制动力矩T_bf和转速ω _w之间的关系式:

Tbf=Teigi0(4)

n=60ωwigi02π(5)

Tbf=77.928(0.0062+0.0016pmax+ 0.0000330ωwigi0π)Veigi0, (ωw≥ωw0)77.928(0.0302+0.0016pmax)Ve800·30ωwigi0πigi0, (0< ωw< ωw0)(6)

式中:i_g为变速器传动比; i₀为主减速器传动比; ω _w0为n=800 r/min时对应的驱动轮转速。

考虑到高速转向车辆在发动机制动工况下可能出现驱动轮反转的情况, 假设驱动轮反转与正转时同一转速对应的制动力矩大小相等方向相反。因此驱动轮上的制动力矩与转速的关系式为:

Tbf=sgn(ωw)·77.928(0.0062+0.0016pmax+ sgn(ωw)·0.0000330ωwigi0π)Veigi0, (|ωw≥ωw0)77.928(0.0302+0.0016pmax)Ve800·30ωwigi0πigi0, (|ωw< ωw0)(7)

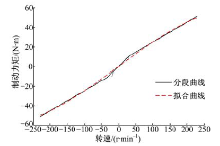
由于该表达式导数不连续, 不利于仿真计算, 在某型发动机上, 其排量为1.39 L, 最大爆发压力为6 MPa, 变速器和主减速器传动比分别为0.795、3.227, 采用等距取点拟合的方法得到发动机制动工况下, 作用在驱动轮上的制动力矩的拟合计算式如式(8)所示, 对应的拟合曲线如图1所示。

Tbf=-7.695×10-7ωw3+0.2571ωw(8)

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 驱动轮上反拖力矩与驱动轮转速的关系曲线Fig.1 Curve of Tbf-ω w on driving wheel

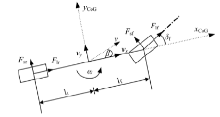
在汽车平面运动的动力学研究中, 采用如图2所示的单轨车辆模型。根据上述分析, 高速行驶车辆在转弯时, 针对利用发动机制动使车辆减速转弯的情况, 建立发动机制动工况下, 五自由度平面运动非线性动力学车辆系统方程如式(9)所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 单轨车辆模型Fig.2 Vehicle bicycle model

v'y=-vxω+[Flfsinδf+Fsfcosδf+Fsr-sgn(vy)Cair_yAL_yρ2vy2]/mω'=[(Flfsinδf+Fsfcosδf)lf-Fsrlr]/Izv'x=vyω+[Flfcosδf-Fsfsinδf+Flr-sgn(vx)Cair_xAL_xρ2vx2]/mω'f=(-Tbf-ReFlf)/Jω'r=(-Tbr-ReFlr)/J(9)

式中:m为整车质量; I_z为绕z轴的转动惯量; v_x为纵向速度; v_y为侧向速度; ω 为横摆角速度; ω _f为前轮角速度; ω _r为后轮角速度; l_f为前轴距; l_r为后轴距; J为车轮转动惯量; δ _f为前轮转角; C_{air_x}、C_{air_y}分别为纵向和侧向风阻系数; A_{L_x}、A_{L_y}分别为纵向和侧向迎风面积; ρ 为空气密度; T_bf、T_br分别为前后轮制动力矩; R_e为车轮转动半径; F_1f、F_1r、F_sf、F_sr分别为前后轮纵向和侧向轮胎力。具体的车辆参数如下:m=1500 kg; I_z=3000 kg· m²; l_f=1.2 m; l_r=1.3 m; J=1 kg· m²; C_{air_x}=0.3; C_{air_y}=0.4; A_{L_x}=1.7 m²; A_{L_y}=3.5 m²; ρ =1.2258 kg/m³; R_e=0.307 m。

关于模型方程的几点说明:

(1) 模型中引入了符号函数(sgn)来描述空气阻力。在汽车失稳过程中, 行驶方向有前、后、左、右多种情况, 空气阻力的方向始终与行驶方向相反, 所以要获得速度的符号, 并通过符号函数给车辆施加与行驶方向相反的空气阻力。

(2) 稳态轮胎力的计算方法采用经典的魔术公式, 如式(10)所示:

F=Dsin{Carctan[Bx-E(Bx-arctanBx)]}(10)

式中:B、C、D、E为参数, 参数值如表1所示; F为轮胎纵向力或侧向力; x为轮胎滑移率或侧偏角。

表1

Table 1

表1(Table 1)

表1 纵向与侧向轮胎力参数 Table 1 Longitudinal and lateral tyre parameters 轮胎参数 B C D E 纵向前轮 11.275 1.56 2574.8 0.4109 纵向后轮 18.631 1.56 1749.6 0.4108 侧向前轮 11.275 1.56 2574.7 -1.9990 侧向后轮 18.631 1.56 1749.7 -1.7908

表1 纵向与侧向轮胎力参数 Table 1 Longitudinal and lateral tyre parameters

为了便于计算机分析, 滑移率方程采用式(11):

k=ωwRe-vwxvwx(11)

前、后轮的轮胎侧偏角的表达式分别如式(12)和(13)所示:

αf=δf-arctanvy+ωlfvx(12)

αr=δr-arctanvy-ωlrvx(13)

对于轮胎混合滑移, 采用Pacejka提出的模型进行分析, 具体计算步骤按照式(14)进行^[13]。

Flf=Flf0GxFlr=Flr0GxGx=cosarctanBg, xααBg, xα=rx, 1cosarctanrx, 2kFsf=GyFsf0Fsr=GyFsr0Gy=cosarctanBg, ykkBg, yk=ry, 1cosarctanry, 2α(14)

式中:v_wx为轮心处的纵向速度; δ _r为后轮转角, δ _r=0; F_1f0、F_1r0、F_sf0、F_sr0为稳态下前、后车轮纵向力和侧向力, 其大小可以用魔术式(10)计算; G_x、G_y为轮胎力混合滑移修正函数; r_{x, 1}、r_{x, 2}、r_{y, 1}、r_{y, 2}为轮胎力混合滑移修正系数, 数值分别为35、40、40、35。

(3)前轮转角的输入采用如下形式:

δf=Asin2πf(15)

式中:A为前轮转角幅值; f为前轮转角变化频率。

为验证车辆系统模型的正确性, 进行了制动器制动工况和发动机制动工况的仿真试验。

取前轮转角变化频率f=0.5 Hz, 幅值A=0.04, 单初值点的侧向速度v_y和横摆角速度ω 均为零, 纵向初速度v_x=30 m/s。研究高速转向条件下, 有、无发动机制动时, 系统各状态变量的对比分析。

图3~图6给出了制动器制动作用条件下, 当T_bf=360 N· m、T_br=190 N· m时的数值计算结果。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 制动器制动时系统相空间特性Fig.3 Phase space trajectory on braking condition

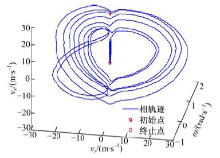
图3为T_bf=360 N· m、T_br=190 N· m时, v_x-v_y-ω 系统相空间特性, 图4为图3在v_y-ω 平面的相轨迹图。通过相轨迹曲线可以看出, 当T_bf=360 N· m、T_br=190 N· m时, 系统的相轨迹为准周期环面。在整个仿真周期内, 纵向速度v_x由初始值开始逐渐减小直至零点; 侧向速度v_y和横摆角速度ω 的绝对值由初始值开始准周期振荡, 并最终减小到零点。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 制动器制动时平面的相轨迹图Fig.4 Plane trajectory on braking condition

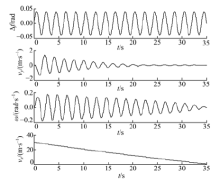
通过观察图5中状态变量的时间序列也可以看到与上述一致的结果。图6中可以看到仿真终止时, 汽车前、后轮角速度都达到零点, 与上述结论相吻合。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 制动器制动时系统状态变量的变化图Fig.5 Time series of state variables on braking condition

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 制动器制动时前、后轮角速度变化Fig.6 Angular velocity of front and rear wheel on braking condition

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 发动机制动时系统相空间特性Fig.7 Phase space trajectory on engine braking condition

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 发动机制动时平面的相轨迹图Fig.8 Plane trajectory on engine braking condition

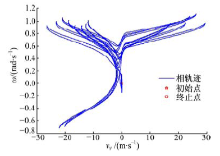
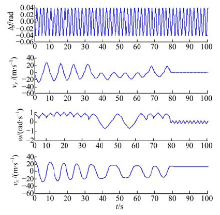
图7~图10给出了发动机制动作用时, 系统在整个发动机制动过程中的数值计算结果。图7为系统状态变量v_x-v_y-ω 在相空间内的相轨迹。与T_bf=360 N· m、T_br=190 N· m时的相轨迹相比, 系统的相轨迹出现了不规则运动, 表征车辆系统的失稳运动。通过图9中状态变量的部分时间序列可以看到:系统的状态变量尽管开始出现不稳定的趋势, 但最终都减小到零点附近。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 发动机制动时系统状态变量时间序列图Fig.9 Time series of state variables on engine braking condition

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 发动机制动时Tbf-ω f关系曲线Fig.10 Curve Tbf-ω f of driving wheel on engine braking condition

结合实际经验可知, 高速行驶车辆在转弯过程中, 若只利用发动机制动实现汽车减速转弯, 由于车辆系统为一个耗散系统, 无论在整个运动过程中汽车是否失稳, 经过足够长的时间, 系统能量最终耗尽, 汽车停止运动。

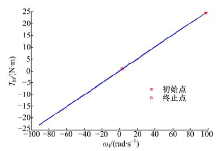
仿真结果证明了所建模型的合理性。由图10中前轮反拖力矩和前轮转速关系曲线图看出, 仿真终止时, 前轮转速和反拖力矩都达到零点, 同样证明了本文模型与实际状况一致。

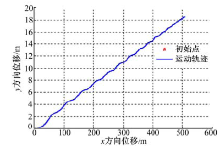
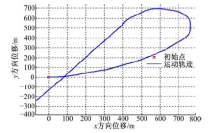
图11给出了T_bf=360 N· m、T_br=190 N· m时, 车辆的运动轨迹图。从图11中可以看到, 该条件下车辆稳定运动且能够保持正常的“ S” 型路线。图12中发动机制动作用下车辆的运动轨迹图表明, 发动机制动作用下车辆失稳, 并且超出车辆正常的运动范围, 行驶路径发生了很大变化。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 制动器制动时车辆运动轨迹Fig.11 Motion trajectory of vehicle on braking condition

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 发动机制动时车辆运动轨迹Fig.12 Motion trajectory of vehicle on engine braking condition

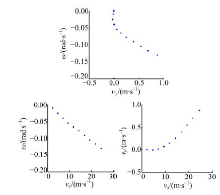
图13和图14为制动器制动, 即T_bf=360 N· m、T_br=190 N· m时, 系统各状态变量的庞加莱截面和功率谱密度图的仿真结果。

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 制动器制动时庞加莱截面Fig.13 Poincare section of phase trajectory on braking condition

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 制动器制动时功率谱密度图Fig.14 Power spectral density diagram of each state variable on braking condition

图13为按每一个周期求解方程一次的方法取值得到的相轨迹的庞加莱截面图。由图13中各个状态变量的截面图看出, 这是典型的准周期运动。

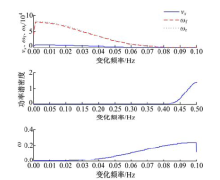
图14为各个状态变量的功率谱密度图, 可以看到各个状态变量的功率谱密度均呈典型的准周期运动的单峰值分布特征。

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 发动机制动时庞加莱截面图Fig.15 Poincare section of phase trajectory on engine braking condition

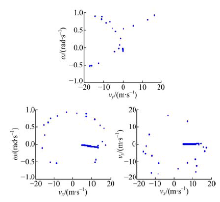
图15和图16为发动机制动作用时系统各状态变量的庞加莱截面和功率谱密度图的仿真结果。

图16

Fig.16

	Figure Option ViewDownloadNew Window
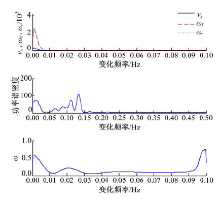	图16 发动机制动时功率谱密度图Fig.16 Power spectral density diagram of each state variable on engine braking condition

与制动器制动, 即T_bf=360 N· m、T_br=190 N· m时, 系统各状态变量的庞加莱截面图相比, 图15中的庞加莱截面显示:在发动机制动作用下, 系统的庞加莱截面已过渡到成片的密集点。同时, 图16中的侧向速度和横摆角速度的功率谱密度也开始出现了宽频多峰的特征。这些都表明系统出现混沌特征, 证明了上述相空间中出现的不规则运动的实质是系统出现混沌运动。

上述仿真结果表明, 高速转向时在发动机制动作用下, 系统各状态变量会出现不规则变化, 表征车辆失稳运动的产生。庞加莱截面与功率谱密度的仿真结果表明, 发动机制动引起的车辆失稳运动, 本质上是一种混沌运动。

提出了发动机制动工况下, 发动机制动力矩的一种解析表达方法, 建立了适用于发动机制动工况的车辆系统模型。在该车辆模型的基础上, 利用相平面方法仿真分析了有、无发动机制动作用下, 高速转向车辆的动力学特性。仿真结果在验证本文模型合理性的同时表明了发动机制动会导致高速转向行驶车辆的失稳运动。庞加莱截面和功率谱密度数值识别方法的分析结果揭示了在发动机制动作用下, 高速转向车辆失稳运动的本质是混沌运动。