基于动态规划的复合电源能量管理优化

引用本文

宋传学, 周放, 肖峰. 基于动态规划的复合电源能量管理优化. 2017, 47(1): 8-14
SONG Chuan-xue, ZHOU Fang, XIAO Feng. Energy management optimization of hybrid energy storage system (HESS) based on dynamic programming. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 8-14 复制到剪切板

Permissions

基于动态规划的复合电源能量管理优化

宋传学, 周放, 肖峰

吉林大学汽车仿真与控制国家重点实验室,长春 130022

作者简介:宋传学(1959-),男,教授,博士生导师.研究方向:汽车系统动力学.E-mail:songchx@126.com

基金:吉林省科技厅重点科技攻关项目(20150204017GX).

摘要

以复合电源能耗和电池组容量损失最小化为目标建立多目标优化模型,将电池组容量损失视为状态变量,将多目标优化问题转化为单目标多状态形式,并应用动态规划进行求解,得到Pareto解集。分析优化结果,提取了数条功率分配规律,并基于此提出基于规则的能量管理策略。对控制策略进行仿真验证,结果表明:与动态规划结果相比,复合电源能耗增加1%,电池容量损失增加0.4%,达到了与动态规划相近的效果,在线能量管理策略同时在两个目标上近似最优。

关键词: 车辆工程; 复合电源; 能量管理; 多目标动态规划; 容量损失

中图分类号:U461.8 文献标志码:A 文章编号:1671-5497(2017)01-0008-07

Energy management optimization of hybrid energy storage system (HESS) based on dynamic programming

SONG Chuan-xue, ZHOU Fang, XIAO Feng

State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,China

Abstract

A multi-objective optimization method aiming at minimizing HESS energy consumption and battery capacity loss is proposed. The battery loss is considered as a state variable, then, the multi-objective optimization problem is transformed into single objective with two state variables. The optimization problem is solved using dynamic programming algorithm, thus obtaining the Pareto-optimal sets. The optimization result is analyzed and a series of control rules are acquired, then, based on these rules, a rule-based power slitting strategy is proposed. Finally, the proposed strategy is simulated under Urban Dynamometer Driving Schedule condition. Results show that, compared with dynamic programming results, HESS energy consumption increases by 1%, and battery capacity loss increases by 0.4%, similar effect with dynamic programming is achieved. This proposed online ene4gy management is sub-optimal on both targets.

Keyword: vehicle engineering; hybrid energy storage system; energy management; multi-objective dynamic programming; capacity losses

Show Figures

0 引言

电池寿命是制约纯电动汽车性能的关键因素之一。车辆在行驶过程中, 功率需求是高度非线性的, 包含了大量的瞬态分量。由于电池的功率密度较小, 根据电压限制和行驶里程为电动汽车匹配电池组后, 电池组往往难以应对行驶过程中的峰值功率; 同时功率波动和峰值功率会加速电池容量衰减, 缩短电池寿命^[1]。因此, 在电源中引入具有高功率密度的超级电容, 与电池组成复合电源(Hybrid energy storage system, HESS)是一种有效延长电动汽车电池寿命的方法。

复合电源能量管理策略是其能否发挥优势的关键因素, 常用的有基于规则的控制策略(包括模糊控制)、基于离线优化的控制策略(如动态规划、模拟退火算法^[2]等)以及模型预测算法^[3]和随机动态规划等。模糊控制鲁棒性较好, 但无法保证全局最优; 遗传算法和粒子群算法无法保证全局最优, 且需要已知全局信息; 模型预测和随机动态规划的效果对于预测信息的准确性有很高的敏感度, 实时应用不易达到较好的效果。此外许多研究是以HESS能耗或者电池寿命为目标^[4]进行优化, 较少有文献将两者同时考虑; 而HESS能耗和电池组寿命两个目标往往是冲突的, 只考虑一个目标会使另一个目标恶化, 因此能量管理策略的制定需要同时考虑对两个目标的影响。

基于此, 本文以车载复合电源为研究对象, 同时考虑电池容量损失和复合电源电耗两个目标, 应用动态规划(Dynamic programming, DP)算法对复合电源能量管理策略进行离线优化, 并根据优化结果设计在线逻辑门限能量管理策略, 保证能量管理策略易于实施, 并能在两个目标达到次优。

1 复合电源模型

1.1 复合电源结构

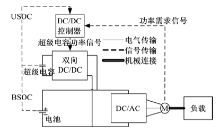
根据主控器件的不同, HESS的拓扑结构分为全主动式、半主动式和被动式。综合考虑成本和控制实现等方面的问题, 本文选择超级电容主动并联结构。图1为复合电源的拓扑结构, 超级电容通过双向DC/DC变换器与电池并联, 电池组直接与电机控制器连接, 根据采集的功率需求信号及电源状态变量, 能量管理系统(EMS)计算超级电容功率输出和电池输出剩余功率^[5]。

	Figure Option View Download New Window
	图1 复合电源拓扑结构Fig.1 HESS topology

1.2 部件模型

对各动力源部件建立适合于DP算法的数学模型。DP算法需要获取各部件的能量消耗以及电流信息, 因此电池模型采用主要反映内阻信息的Rint模型, 同时满足简单和精确的要求, 模型电路如图2(a)所示。由于一个循环工况时间较短, 在这个时间尺度上, 超级电容不用考虑高频和漏电现象, 采用RC电路模型就能达到足够的精确度, 模型电路如图2(b)所示。

	Figure Option View Download New Window
	图2 电池和超级电容模型Fig.2 Models of battery and ultracapacitor

根据能量管理策略计算出部件功率需求后, 电池和超级电容的电流及荷电状态根据式(1)~(4)进行计算:

$I_{bat} = \frac{U_{bat} - \sqrt[]{U_{bat}^{2} - 4 P_{bout} R_{bat}}}{2 R_{bat}}$ (1)

$I_{UC} = \frac{U_{UC} - \sqrt[]{U_{UC}^{2} - 4 P_{ucout} R_{UC}}}{2 R_{UC}}$ (2)

$BSO C_{t_{p}} = BSO C_{t_{0}} - \frac{1}{C_{bat}} \int_{t_{0}}^{t_{p}} I_{bat} dt$ (3)

$USO C_{t_{p}} = USO C_{t_{0}} - \frac{1}{C_{UC} U_{UC}} \int_{t_{0}}^{t_{p}} I_{UC} dt$ (4)

式中:I_bat和I_UC为电池和超级电容电流, A; U_bat和U_UC分别为电池额定电压、超级电容最高电压, V; P_bout和P_ucout为电池组和超级电容组功率需求, W; BSOC和USOC为电池荷电状态; C_bat为电池安时容量, Ah; C_UC为超级电容容量, F。

将电机和DC/DC变换器的损失/效率模型以查表的形式加入控制流程进行计算。图3为电机在不同转速及转矩下的能量损失和DC/DC在不同传递功率时的效率。

	Figure Option View Download New Window
	图3 电机损失和DC/DC效率Fig.3 Electrical machine losses and DC/DC efficiency

1.3 电池容量损失模型

文献[6]提出了一种半经验的静态电流下的电池容量损失模型, 其中电池的容量损失百分比与累计电荷流通量呈幂率关系, 同时引入阿伦尼乌斯关系代表温度的影响, 模型表达式如下:

$\begin{matrix} Q_{loss} = Bexp (- \frac{E_{a}}{RT}) (A_{h})^{z} \end{matrix}$ (5)

式中:Q_loss为容量损失百分比, %; $\begin{matrix} B \end{matrix}$ 为指前因子; E_a为活化能, kJ/mol; $\begin{matrix} R \end{matrix}$ 为气体摩尔常数, J/(k· mol); $\begin{matrix} T \end{matrix}$ 为绝对温度, K; A_h为累计电荷, Ah; $\begin{matrix} z \end{matrix}$ 为幂率因子, 根据拟合得到, 值为0.55。

为了能表示在行驶工况下动态电流对电池的容量损失的影响, 对式(5)进行求导^[7]:

$\begin{matrix} {\overset{\cdot}{Q}}_{loss} = zB \exp (\frac{- E_{a}}{zRT}) (A_{h})^{z - 1} \end{matrix}$ (6)

其中, A_h由式(5)反推计算得出:

$\begin{matrix} A_{h} = {(\frac{Q_{loss} \exp (\frac{- E_{a}}{RT})}{B})}^{\frac{1}{z}} \end{matrix}$ (7)

将式(7)带入式(6)并进行离散化处理:

$\begin{matrix} Q_{loss, p + 1} - Q_{loss, p} = Δ A_{h} z B^{\frac{1}{z}} \exp (\frac{- E_{a}}{zRT}) Q_{loss, p}^{\frac{z - 1}{z}} \end{matrix}$ (8)

式中: $\begin{matrix} Q_{loss, p} 和 Q_{loss, p + 1} 为 t_{p} 和 t_{p + 1} 时刻的容量损失, %; Δ A_{h} 为 t_{p} 至 t_{p + 1} \end{matrix}$ 时间段内累计电荷, 单位是Ah。累计电荷根据式(9)计算:

$\begin{matrix} Δ A_{h} = \frac{1}{3600} \int_{p}^{t_{p + 1}} | I_{bat} | dt \end{matrix}$ (9)

在式(8)中, $\begin{matrix} B \end{matrix}$ 和E_a都是与电池电流倍率(Current rate, C_rate)相关的变量, 电流倍率为C/2、2C、6C、10C时, B值分别为31 630、21 681、12 934、15 512。

对 $\begin{matrix} B \end{matrix}$ 值及电流倍率的关系进行拟合:

$\begin{matrix} B = - 47.84 C_{rate}^{3} + 1215 C_{rate}^{2} - 9419 C_{rate} + 36040 \end{matrix}$ (10)

E_a与电池电流倍率的关系表示如下:

$\begin{matrix} E_{a} = - 31700 + 370.3 C_{rate} \end{matrix}$ (11)

2 动态规划算法

动态规划(Dynamic programming, DP)通常用于求解多阶段决策最优化问题, 在这类问题中, 可通过作出一组选择来达到最优解。由于HESS功率分配策略的优化可以视为以离散时间为阶段的多阶段决策问题, 在每个阶段合理地分配车辆的功率需求给不同的能量源, 以获取最优的目标性能, 因此, 动态规划适合于解决HESS的能量管理优化问题^{[8, 9]}。

在本文提出的能量管理问题中, 有两个目标:一是HESS总能耗最小; 二是电池容量损失最小。式(8)的计算包含了累计的容量损失, 因此当前阶段的容量损失与之前所有阶段的选择都相关, 不满足最优子结构的性质, 因此不能直接作为动态规划的优化目标。

将电池容量损失作为状态变量, 将HESS总能耗作为优化目标, 把多目标优化转化为单目标优化, 同时选择USOC作为另外一个状态变量, 然后应用动态规划求解, 在终点处求得不同电池容量损失下的HESS最小能耗^[10]。

由于需要在终端计算出不同容量损失时的能耗, 因此在动态规划求解时须采用正向迭代, 子问题是求解初始状态转移到当前状态变量组时, HESS的最小能耗; 每一阶段下, 能耗矩阵求解和插值寻优同时进行, 在终点处得到所有可达状态下的HESS最小能耗。

最终, 优化问题表述如下:

$\begin{matrix} J = \min \overset{end}{\sum_{t = 1}} (E_{bat} (t) + E_{UC} (t)) \end{matrix}$ (12)

式中:E_bat和E_UC分别是电池组和超级电容组能耗, kJ。

优化问题受动力源性能约束, 如式(13)所示:

$\begin{matrix} subject to \{\begin{matrix} I_{UC, \min} \leq I_{UC} \leq I_{UC, \max} \\ I_{bat, \min} \leq I_{bat} \leq I_{bat, \max} \\ 0.5 \leq USOC \leq 1 \\ USO C_{init} = USO C_{end} \\ 4 R_{bat} P_{bout} \leq U_{bat}^{2} \end{matrix} \end{matrix}$ (13)

式中:I_{UC, min}和I_{UC, max}分别为超级电容最大充放电电流, A; I_{bat, min}和I_{bat, max}分别为电池组最大充放电电流, A。

输入变量:电源功率需求P_demand(Δ t=1 s);

状态变量:USOC(Δ USOC=0.5%)和Q_loss(Δ Q_loss=0.0001%);

决策变量:P_ucout(由USOC的变化反推获得);

优化过程伪代码如下:

I、j、k、m分别表示阶段、状态变量组以及决策变量的标号。首先根据状态转移前后的USOC值求出超级电容能耗E_UC, 然后根据E_UC计算超级电容输出功率P_ucout:

$\begin{matrix} \begin{matrix} E_{UC} (i, j, k, m) = 0.5 C U_{UC}^{2} (USO C^{2} (1, m) - \\ USO C^{2} (1, j)) (14) \\ P_{ucout} (i, j, k, m) = E_{UC} (i, j, k, m) - \\ {(\frac{E_{UC} (i, j, k, m)}{U_{UC} USOC (1, m)})}^{2} R_{UC} \end{matrix} \end{matrix}$ (15)

根据功率需求P_demand和超级电容输出功率P_ucout的差值及DC/DC的效率计算出电池输出功率P_bout, 然后根据图2所示模型和式(1), 计算电池电流I_bat和能耗E_bat:

$I_{bat} (i, j, k, m) = \frac{U_{bat} - \sqrt[]{U_{bat}^{2} - 4 R_{bat} P_{bout} (i, j, k, m)}}{2 R_{bat}}$ (16)

$E_{bat} (i, j, k, m) = I_{bat} (i, j, k, m) U_{bat}$ (17)

进而计算出该次状态变量组转移对应的HESS总能耗E_step:

$\begin{matrix} E_{step} (i, j, k, m) = E_{UC} (i, j, k, m) + E_{bat} (i, j, k, m) \end{matrix}$ (18)

假设决策前电池累计容量损失为x, 结合式(8)~(11)计算x, 如式(19)所示:

$\begin{matrix} Q_{loss} (1, k) - x = Δ A_{h} zexp (\frac{- E_{a}}{zRT}) B^{\frac{1}{z}} x^{\frac{z - 1}{z}} \end{matrix}$ (19)

根据状态变量组(USOC(1, m), x), 插值得到此决策下状态转移前最小HESS能耗E_{total, temp}, 遍历所有决策, 对比并存储转移后最小总能耗E_opt及对应的USOC路径:

$\begin{matrix} \begin{matrix} if E_{opt} (i + 1, j, k) > \\ E_{step} (i, j, k, m) + E_{total, temp} (i, j, k, m) \\ t h en E_{opt} (i + 1, j, k) = \\ E_{step} (i, j, k, m) + E_{total, temp} (i, j, k, m) \\ pat h (i, j, k) = m \end{matrix} \end{matrix}$ (20)

矩阵 $\begin{matrix} E_{opt} \end{matrix}$ 储存从初始状态到当前阶段目标状态变量组时最小HESS能耗, 矩阵 $\begin{matrix} P_{pat h} \end{matrix}$ 储存到达此状态变量组的上一步最优USOC。优化阶段完成后, 根据终点状态变量组的选择和矩阵 $\begin{matrix} P_{pat h}, \end{matrix}$ 即可从终点反向推导, 求得最优状态及控制序列。

状态变量的增加会使计算量急剧增加, 为降低计算成本, 对算法做以下两方面优化:

(1)根据超级电容电流限制计算不同USOC的可达状态并进行保存, 根据计算得到:可达状态由101个下降到7个, 即状态变量组的可能决策量将为7^[11], 对比计算次数为7次。

(2)优化前, 根据式(19)计算不同电流倍率作用下, 达到不同电池容量损失时的决策前电池容量损失, 存为二维表格; 在DP程序中, 式(20)的计算从解非线性方程变为计算二维插值, 耗时大大缩短。

3 优化结果分析

动态规划计算时, 电池组开路电压、电池组电阻和超级电容电阻都视为定值, 优化参数如表1所示。

表1 DP优化参数 Table 1 DP optimization parameters

图4为DP优化结果, 展示了终值USOC为0.7时, HESS能耗随最终电池容量损失的变化趋势。优化结果共包含238组解, 即图4中的蓝色点集(包括红色覆盖的部分)。根据Pareto Front的定义, 从解集中选出非支配集(简称Pareto集), 如图4中红色点集所示。非支配集中的解有如下性质:解集两两之间互为非支配关系, HESS能耗和电池容量损失两者减小其中一个值, 都要以增大另一个值为代价, 最终的解从红色点集中选取。

	Figure Option View Download New Window
	图4 动态规划优化结果Fig.4 DP optimization results

在Pareto集以外的解集, HESS能耗随着电池容量损失增大而增大, 这是由于除了应对必要的功率需求外, 电池组与超级电容组之间还进行了不必要的能量流动, 增加了电池组的累计电荷, 引起容量损失增加; 同时这种情况增加了电源的内部损耗, 导致两个目标值同时增大。在Pareto解集内, 两个目标相互冲突, 这是由于电池组容量损失减小时, 电池组应对功率和电流输出减小; HESS能耗减小时, 电池组应对功率和电流输出增大, 故而出现这种冲突关系。

图4所示的Pareto集中, 不考虑电池容量损失时, HESS的最小能耗可以达到4740 kJ, 对应的电池容量损失为0.0651%; 不考虑HESS能耗时, 电池容量损失最小能够达到0.0532%, 对应的HESS总能耗为5050 kJ; 同时可以看出, 在Pareto解集中, 随着电池容量损失的显著增加, HESS能耗减小较慢, 因此选择电池容量损失相对较小的一组数据作为最优解, 如图4中黑色点所示, 此时对应的最优解为HESS能耗4830 kJ, 电池容量损失为0.0573%。

图5为Pareto集中单个目标最小对应的两个解、所选解以及电池单独供电4种情况下, HESS总能耗和电池容量损失随循环工况的变化。HESS能耗在整个时间历程内的变化趋势相似且数值上相差很小, 而电池容量损失则在整个历程内变化明显, 说明所选的解偏重减小电池容量损失是合理的。

	Figure Option View Download New Window
	图5 四种情况下目标值变化Fig.5 Variation of two objectives under four conditions

Pareto集中任何两个解之间相比都无法说谁是更优解, 如何选择取决于希望达到什么样的效果, 即在HESS能耗和电池容量损失之间如何平衡。

4 基于规则的能量管理策略

由于全局工况信息需要提前获知, 通过动态规划得到的全局最优能量管理策略无法实时应用, 但是通过优化结构可以了解HESS的性能潜力, 同时通过分析优化结果能够获取一些规律, 用于在线能量管理策略的制定和评价。

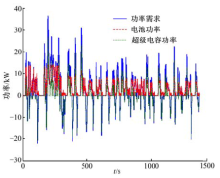
图6是所选最优解对应的各动力源功率输出, 可以看出电池在制动过程中不吸收任何能量, 还有一个极小的功率输出; 在上半部分, 功率需求较大时, 电池输出一个较大的相对平稳的功率, 功率需求较小时, 电池输出一个较小的相对平稳的功率。

	Figure Option View Download New Window
	图6 最优功率分配Fig.6 Optimal power splitting

图7更为直观地展现了各动力源功率输出与功率需求的关系特性。可以看出, 在功率需求为负(再生制动)时, 超级电容几乎吸收了所有的制动能量, 同时电池为超级电容提供一个不超过2 kW的功率; 功率需求在0~5 kW时, 超级电容不工作, 电池单独供电; 功率需求在5~20 kW时, 超级电容与输出功率呈线性关系, 电池输出8 kW或者13 kW左右的功率;

	Figure Option View Download New Window
	图7 功率输出和部件功率需求的关系Fig.7 Relationship between power output and demand

功率需求超过20 kW后, 超级电容仍与功率需求呈线性关系, 电池补足剩余功率, 但不超过14 kW。

根据以上分析, 得到基于规则(Rule-based, RB)的能量管理策略, 遵循以下几点:①超级电容吸收全部再生制动能量, 同时电池为超级电容以恒功率P_ch供电; ②功率需求不超过P_low时, 电池单独供电; ③功率需求在P_low和P_high之间时, 电池以P_min供电, 超级电容补足剩余需求; ④功率需求超过P_high之后, 电池以P_max供电, 超级电容补足剩余需求; ⑤功率需求为正时, 如果USOC小于0.5, 则电池单独供电, 并且向超级电容充电。

调节P_ch、P_min、P_max、P_high和P_low, 得到合适的参数。表2记录了能量管理策略使用不同参数时, HESS对应的结果。

表2 参数调整及结果 Table 2 Parameters adjustment and corresponding results

选择第3组参数作为RB策略参数进行仿真, 各个动力源的功率输出结果如图8所示。可以看出, 在整个行驶过程中, 电池在绝大多数的时间的功率输出比较小, 即电流较小, 从而有效减少电池的容量损失; 在200~250 s, 电池出现了三次较大的功率输出, 这是由于RB策略参数固定, 且无法像DP算法那样获取全局工况信息。

	Figure Option View Download New Window
	图8 基于规则的策略仿真结果Fig.8 Rule-based strategy simulation results

计算电池单独供能时的能耗和容量损失, 并将其和DP结果以及RB策略列于表3作为对比。与DP优化结果相比, 本文控制策略容量损失增加1%, HESS能耗增加0.4%, 达到了相近的结果; 与电池组单独供电相比, 本文控制策略电池容量损失减少了21.5%, HESS能耗减少了4%。RB策略经过参数调整能够近乎达到DP优化结果的效果, 同时保证了HESS能耗和电池组容量损失近似最优。

表3 DP优化, RB策略与电池单独供能对比 Table 3 Comparison of DP, RB strategy and battery only

5 结论

(1)对车载复合电源能量管理策略进行优化, 以HESS能耗和电池组容量损失最小化为目标建立多目标优化问题, 并转化为单目标多状态形式, 使用动态规划进行求解, 得到了问题的Pareto集。

(2)对优化结果分析表明:最优能量管理策略中, 超级电容功率和HESS功率需求呈现了分段线性的关系, 为在线策略的制定提供了依据。

(3)根据优化结果制定了基于规则的能量管理策略, 仿真结果表明:能量管理策略有效地减小了HESS的能耗和电池组容量损失, 达到了和动态规划结果近似的效果, 是一种次优且易于实施的在线能量管理策略。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Jossen A. Fundamentals of battery dynamics[J]. Journal of Power Sources, 2006, 154(2): 530-538. [本文引用:1]
[2]	王斌, 徐俊, 曹秉刚, 等. 采用模拟退火算法的电动汽车能量管理系统优化[J]. 西安交通大学学报, 2015, 49(8): 90-96. Wang Bin, Xu Jun, Cao Bing-gang, et al. Optimization of energy management system with simulated annealing approach for hybrid power source in electric vehicles[J]. Journal of Xi'an Jiaotong University, 2015, 49(8): 90-96. [本文引用:1]
[3]	Song Z Y, Hofmann H, Li J Q, et al. Energy management strategies comparison for electric vehicles with hybrid energy storage system[J]. Applied Energy, 2014, 134: 321-331. [本文引用:1]
[4]	Song Z Y, Li J Q, Han X B, et al. Multi-objective optimization of a semi-active battery/supercapacitor energy storage system for electric vehicles[J]. Applied Energy, 2014, 135: 212-224. [本文引用:1]
[5]	Miller P M, Prummer M, Schnewly A. Power electronic interface for an ultracapacitor as the power buffer in a hybrid electric energy storage system[DB/OL]. [2015-10-11]. http://www.maxwell.com/images/documents/whitepaper_powerelectronicsinterface.pdf. [本文引用:1]
[6]	Wang J, Liu P, Hicks-Garner J, et al. Cycle-life model for graphite-LiFePO4 cells[J]. Journal of Power Sources, 2011, 196(8): 3942-3948. [本文引用:1]
[7]	Song Z Y, Hofman H, Li J Q, et al. Optimization for a hybrid energy storage system in electric vehicles using dynamic programming approach[J]. Applied Energy, 2015, 139: 151-162. [本文引用:1]
[8]	邹渊. 车辆驱动系统建模与优化[M]. 北京: 机械工业出版社, 2015. [本文引用:1]
[9]	钱立军, 邱利宏, 辛付龙, 等. 插电式四驱混合动力汽车能量管理控制策略及其优化[J]. 农业工程学报, 2015, 31(13): 68-76. Qian Li-jun, Qiu Li-hong, Xin Fu-long, et al. Energy management control strategy and optimization for plug-in 4WD hybrid electric vehicle[J]. Transactions of the CSAE, 2015, 31(13): 68-76. [本文引用:1]
[10]	于远彬. 车载复合电源设计理论与控制策略研究[D]. 长春: 吉林大学汽车工程学院, 2008. Yu Yuan-bin. Study on the design theory and control method issues of synergic electric power system on bus[D]. Changchun: College of Automotive Engineering, Jilin University, 2008. [本文引用:1]
[11]	申彩英. 串联混合动力汽车能量优化管理策略研究[D]. 天津: 天津大学电气与自动化工程学院, 2010. Shen Cai-ying. Study on energy optimal management for series hybrid electric vehicles[D]. Tianjin: College of Electrical Engineering & Automation, Tianjin University, 2010. [本文引用:1]

2006

0.0

... 同时功率波动和峰值功率会加速电池容量衰减,缩短电池寿命^[1] ...

2015

0.0

. 2015, 49(8):90-96 DOI:doi:10.7652/xjtuxb201508015

Optimization of energy management system with simulated annealing approach for hybrid power source in electric vehicles

采用模拟退火算法的电动汽车能量管理系统优化

Wang Bin , Xu Jun , Cao Bing-gang

王斌, 徐俊, 曹秉刚

针对电动汽车的混合式复合电源工作模式切换复杂、不利于不同工作模式的功率最优分配问题,提出基于模拟退火算法的复合电源能量管理优化方法.对混合式复合电源的工作模式进行分层讨论,建立能量管理系统的各部件损耗模型,基于不同层次设计能量管理策略.在分层能量管理策略的基础上,采用模拟退火算法降低系统的损耗.搭建混合式复合电源仿真模型和实验台进行仿真和实验. 仿真和实验结果表明:在NYCC和EUDC路况下,混合式复合电源能量管理系统采用模拟退火算法优化比滞环逻辑控制的总损耗降低0.8％和1.1％.混合式复合电源能量管理系统采用模拟退火算法不仅能有效降低系统损耗,实现功率最优分配,而且能及时跟随功率需求,由超级电容提供或吸收峰值功率,保证电池安全.

... 复合电源能量管理策略是其能否发挥优势的关键因素,常用的有基于规则的控制策略(包括模糊控制)、基于离线优化的控制策略(如动态规划、模拟退火算法^[2]等)以及模型预测算法^[3]和随机动态规划等 ...

2014

0.0

2014

0.0

... 此外许多研究是以HESS能耗或者电池寿命为目标^[4]进行优化,较少有文献将两者同时考虑 ...

0.0

... 图1为复合电源的拓扑结构,超级电容通过双向DC/DC变换器与电池并联,电池组直接与电机控制器连接,根据采集的功率需求信号及电源状态变量,能量管理系统(EMS)计算超级电容功率输出和电池输出剩余功率^[5] ...

2011

0.0

2015

0.0

... 为了能表示在行驶工况下动态电流对电池的容量损失的影响,对式(5)进行求导^[7]: ...

2015

0.0

... 由于HESS功率分配策略的优化可以视为以离散时间为阶段的多阶段决策问题,在每个阶段合理地分配车辆的功率需求给不同的能量源,以获取最优的目标性能,因此,动态规划适合于解决HESS的能量管理优化问题^[8,9] ...

2015

0.0

. 2015, 31(13):68-76 DOI:doi:10.11975/j.issn.1002-6819.2015.13.010

Energy management control strategy and optimization for plug-in 4WD hybrid electric vehicle

插电式四驱混合动力汽车能量管理控制策略及其优化

Qian Li-jun , Qiu Li-hong , Xin Fu-long

钱立军, 邱利宏, 辛付龙

为精确计算驾驶员请求转矩，克服模糊逻辑及模糊比例-积分-微分（proportion integration differentiation，PID）需要先验知识的固有缺陷，该文提出利用径向基函数（radial basis function，RBF）神经网络拟合转矩识别系数。考虑到动力部件的瞬态特性，建立了各动力部件及传动系统的动力学模型，制定了基于规则的控制策略并描述了各驱动模式的成立条件及其动力学方程。为减少程序运行时间，提出修正动态规划（correctional dynamic programming，CDP）算法对控制策略进行全局优化。搭建硬件在环试验台架，对控制策略进行了试验。试验结果表明，基于规则和修正动态规划的控制策略均能实现良好的控制效果。引入转矩识别后，车速误差明显减小，燃油经济性提高了4.54%。采用修正动态规划后，燃油经济性进一步提高了14.04%。该文研究方法可以为制定复杂混合动力系统控制策略提供理论依据。

2008

0.0

. 2008, :-

Study on the design theory and control method issues of synergic electric power system on bus

车载复合电源设计理论与控制策略研究[D]

Yu Yuan-bin.

于远彬

搭载有高效、长寿的电量存储装置是混合动力汽车等新能源汽车发挥节能、环保优势的前提和基础,也是新能源汽车能够大批量市场化的关键。为了弥补单一电池和超级电容分别在比功率和比能量方面的不足,本文将高比功率的超级电容和大比能量的蓄电池复合组成即能满足整车性能要求,又能最大限度回收整车制动能量的理想车载电源。论文的创新之处在于提出了电源复合的思想,以弥补单一电源性能的不足。通过合理的匹配,在兼顾成本的同时,保证了电源的性能;提出了新的电源性能评价指标,并制定了复合电源车载使用条件下的设计理论;通过适当控制策略的编写,保证了系统可以高效、长寿地工作,并对控制效果进行评价。

... 将电池容量损失作为状态变量,将HESS总能耗作为优化目标,把多目标优化转化为单目标优化,同时选择USOC作为另外一个状态变量,然后应用动态规划求解,在终点处求得不同电池容量损失下的HESS最小能耗^[10] ...

2010

0.0

... (1)根据超级电容电流限制计算不同USOC的可达状态并进行保存,根据计算得到:可达状态由101个下降到7个,即状态变量组的可能决策量将为7^[11],对比计算次数为7次 ...