从众心理影响下的行人群体行为演化博弈的仿真分析—

引用本文

吴文静, 王占中, 马芳武. 从众心理影响下的行人群体行为演化博弈的仿真分析——以行人过街为例. 2017, 47(1): 92-96
WU Wen-jing, WANG Zhan-zhong, MA Fang-wu. Simulation analysis of evolutionary game of pedestrians' group behaviors under influence of herd behavior: in case of crossing behavior. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 92-96 复制到剪切板

Permissions

从众心理影响下的行人群体行为演化博弈的仿真分析——以行人过街为例

吴文静¹, 王占中¹, 马芳武²

1.吉林大学交通学院,长春 130022

2.吉林大学汽车学院,长春 130022

通讯作者:王占中(1965-),男,教授,博士生导师.研究方向:运输系统规划.E-mail:wangzz@jlu.edu.cn

作者简介:吴文静(1980-),女,副教授,博士.研究方向:运输系统仿真.E-mail:ease_wwj@163.com

基金:国家自然科学基金项目(51278221,51378076); 中国博士后科学基金项目(2013M541307).

摘要

以行人过街为例对从众效应进行研究,提出了从众效应的量化策略。构建了从众心理影响下的行人过街的演化博弈模型。将行人划分为冒险、折中、保守三类,设计了行人群体行为演化的仿真实验。结果表明:群体构成以及违章过街群体占总人群比例对群体行为演化影响显著。最后提出了考虑从众效应的行人社会力仿真模型的改进策略。本文的研究方法扩展了行人行为研究的分析手段,研究结果可为行人仿真模型参数的设置提供参考。

关键词: 交通运输系统工程; 从众效应; 行人过街; 演化博弈

中图分类号:U491 文献标志码:A 文章编号:1671-5497(2017)01-0092-05

Simulation analysis of evolutionary game of pedestrians' group behaviors under influence of herd behavior: in case of crossing behavior

WU Wen-jing¹, WANG Zhan-zhong¹, MA Fang-wu²

1.College of Transportation,Jilin University, Changchun 130022,China

2.College of Automotive Engineering,Jilin University, Changchun 130022,China

Abstract

Taking pedestrians' crossing behavior as the research object, the quantified method of the conformity effect is proposed. The evolutionary game model of pedestrians' crossing behavior under the influence of conformity is constructed. Furthermore, the pedestrians are classified into adventurous, compromise and conservative groups, and a simulation experiment is designed. The results show that the constituent of pedestrians and the proportion of illegal crossing groups have significant influences on the pedestrians' crossing process. At last, an improvement strategy of the social force simulation model considering conformity effect is proposed. The results of this research can enrich and expand the theoretical framework and analytical methods of pedestrians' behavior, and provide reference for setting parameters of pedestrian simulation.

Keyword: engineering of communication and transportation system; conformity effect; pedestrians crossing; evolutionary game

Show Figures

0 引言

行人从众心理及诱发的群体闯红灯行为在我国城市交通中普遍存在, 被称之为“ 中国式过马路” , 它是困扰交通管理者的一大难题。在不确定交通环境下, 从众效应伴随着行人过街行为决策的全过程^[1]。过街行人之间的行为决策存在相互作用关系, 因此行人往往会偏离自己原先的选择而做出符合群体行为偏好的决策^[2]。考虑社会环境对行为决策的影响已有一些研究文献, 例如Han等^[3]建立了社会网络影响下的出行者选择集合动态更新的学习模型, 并运用于购物地点选择行为的研究; Ronald等^[4]研究了社会网络成员间的信息交流对出行者认知与知识更新过程的影响, 并运用于出行计划以及出行地点选择等行为的研究; Zhou等^[5]分析了中国行人在与他人过街行为一致以及不一致两种情况下的行人的主观规范和行为控制, 并提出了行为干预对策; 吴文静等^[6]基于博弈理论分析了参照群体对行人从众过街行为决策的影响。

现有对行人行为的研究中一方面普遍关注于行人群体紧急情况下而不是平常情况下的群体行为; 另一方面, 其主要研究内容包括了行人在移动中的避碰以及路径导航、人群间的动力学特征描述、行为的个体差异性而忽略了对行人的从众心理及通过个体间的交互影响而反映出的群体的行为特征分析。本文以行人群体过街行为为研究对象, 探讨受从众心理影响的行人群体过街行为的演化规律。

1 从众心理影响下行人过街行为决策的博弈分析

1.1 博弈模型构建

供过街行人参照的群体可划分为两大类:违章群体、遵章群体。行人选择加入哪个群体与行人可获得的相应损益相关, 并且随着两个群体数量的动态变化, 行人自身对损益的评估也发生变化, 这一心理过程可借助博弈模型加以解释。

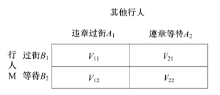
此博弈的一方为某过街行人M, 另一方为与其同时需要过街的其他行人。M面临的决策有两类:一是违章过街, 面临的风险是可能会与机动车有碰撞风险; 二是遵章等待, 但是可能要等待很长的时间。此博弈过程假设其他行人的行为决策是一个不确定因素, M是在不知道其他行人的行为决策的情况下, 与其他行人同时进行决策。此博弈的得益矩阵描述如图1所示。

	Figure Option View Download New Window
	图1 行人过街得益矩阵Fig.1 Payoff matrix of pedestrian’ s crossing behavior

矩阵中的4个元素分别代表行人M在4种可能情况下的得益, 其他行人的得益在此不作考虑。假设在某一时刻, 其他行人的决策用A_i 表示, 行人M的决策用B_j 表示, i、j分为两类, 取值1和2, 分别代表违章过街与遵章等待。选择A_i 的人群占总人群的比例用P(A_i)表示。则行人M选择过街(B₁)或等待(B₂)的期望得益U(B_j)为:

$\begin{matrix} \begin{matrix} U (B_{j}) = \sum_{i} P (A_{i}) V_{ij} \\ i, j = 1, 2 \end{matrix} \end{matrix}$ (1)

1.2 从众效应量化

前者是假设M完全不知道其他人的行为决策, 但是在现实情况下, 过街行人M能够随时观察到其他行人的行为变化, 并且受到从众心理的影响, 随着过街行人 $\begin{matrix} P (A_{i}) \end{matrix}$ 的变化, 行人M的期望得益会发生偏差, 在此用从众效用ComformistValue表示, 且将其重要程度用权重 $\begin{matrix} c \end{matrix}$ 表示, 则期望得益修改为^[7]:

$\begin{matrix} \begin{matrix} U' (B_{j}) = (1 - c) U (B_{j}) + c \times ComformistValue \\ j = 1, 2 \end{matrix} \end{matrix}$ (2)

随着 $\begin{matrix} P (A_{i}) \end{matrix}$ 的增加, 他人行为对行人M的影响程度也随之增加, 将从众效用强度假设为选择人数 $\begin{matrix} P (A_{i}) \end{matrix}$ 的增函数, 则模型最终更改为:

$\begin{matrix} U^{'} (B_{j}) = (1 - c) \sum_{i} P (A_{i}) V_{ij} + cP (A_{j}) \\ i, j = 1, 2 \end{matrix}$ (3)

由于P(A_i)是随时发生变化的, 所以此博弈为复制动态博弈, 随着P(A_i)的变化, 行人M的期望得益会左右摇摆, 直到期望得益达到平衡。

1.3 博弈更新策略

在此假设博弈个体的策略更新根据以下的规则(统计力学的费米函数)进行:

$\begin{matrix} P_{B_{1} - B_{2}} = \frac{1}{1 + \exp [(U'_{B_{1}} - U'_{B_{2}}) / k]} \end{matrix}$ (4)

该规则的意义在于当过街行人M进行策略更新时, M会随机地选取他的一个邻居节点作为参照群体, 如若行人M的初始策略为 $\begin{matrix} B_{1}, \end{matrix}$ 那么受到他人影响后, 行人M会以 $P_{B_{1} - B_{2}}$ 的概率模仿B₂ 的策略。k为噪声参数项, 代表了一种非理性行为的可能。当k→ 0时, 规则变为确定性规则, 即进行非理性选择的概率变为0; 而当k的值比较大时, 此规则又变为随机转变规则。

2 从众心理影响下行人过街行为的仿真分析

2.1 行人类型划分

由现实可知, 由于行人的性别、年龄、职业、个人习惯、偏好等个人属性不同, 每个个体的得益矩阵存在差异性, 在此采用问卷调查的方式收集行人的从众意愿数据。行人根据实际情况作答, 问题为“ 通常在观察到路口违章过街人数达到总人数的多大比例时才会产生从众过街意愿?” 。根据调查数据统计, 当违章过街人数占总人数的比例分别为0、25%、50%、75%、100%时, 行人从众的意愿比例分别为5.4%、6.5%、11.6%、30.2%、46.3%。

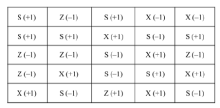
根据上述统计结果, 可将行人大致可以分为3类:保守型(S型)、折中型(Z型)、冒险型(X型)。其中保守型为选择75%(违章参照群体比例)的人群, 折中型为选择50%的人群, 冒险型为选择25%的人群, 选择0与100%的人群为极端人群, 都代表不受参照群体影响的人群, 始终坚持遵章或违章过街。从问卷调查结果可见, 大部分人群的主观意愿为遵章过街, 当然行人在回答问卷时, 受道德规范的影响, 其主观意愿与实际行动之间往往存在偏差。为了研究从众效用的影响途经, 在此主要考虑受从众效用影响的人群, 并将用具有代表性的3种得益矩阵表示此3种人群类型(见图2):

	Figure Option View Download New Window
	图2 行人的类型划分及相应的得益矩阵Fig.2 Constitute of pedestrians and their payoff matrixs

(1)保守型, 其不稳定状态发生在违章过街比例在75%的情况下, 如果大于75%的行人选择违章过街, 行人M也会选择从众, 若考虑到从众效应, 此比例会小于75%, 行人更容易选择从众过街。

(2)折中型, 100%从众过街与100%遵章等待是唯一的平衡状态, 不稳状态发生在群体选择概率为50%的情况下, 只要违章过街人数大于50%, 行人M就会最终向此方偏移, 反之小于50%, 则会选择等待。

(3)冒险型, 不稳定状态发生在违章人群比例在25%的情况下, 若考虑从众效用, 比例会大于25%。

2.2 仿真实验设计

构建受从众心理影响的过街行人群体行为演化的仿真实验系统。系统随机产生一个5× 5的行人群体网格, 网络中包括了行人构成及初始行为决策, 过街(+1)或等待(-1)。行人过街网络的示意图如图3所示。

	Figure Option View Download New Window
	图3 行人过街网络的案例分析Fig.3 A case study of pedestrians network

以位于中心位置的行人为例进行分析, 此行人类型为S, 其初始状态为等待(-1)。从网络结构来看, 通常情况下与行人邻接的8个行人的行为对其影响较大, 在此设置权重为a, 邻接的8人的群体选择概率用P(A'_i)表示, 其他非邻接的16人的群体选择概率用P(A″_i)表示, 则式(3)修改为:

$\begin{matrix} \begin{matrix} U ″ (B_{j}) = (1 - c) (a \sum_{i} P (A'_{i}) V_{ij} + \\ (1 - a) \sum_{i} P (A ″_{i}) V_{ij}) + cP (A_{j}) \\ i, j = 1, 2 \end{matrix} \end{matrix}$ (5)

同时修改式(4)。假设从众效用的权重c取值为0.25, a取0.8, 计算此时网络中与S相邻的8人中违章过街的行人比例P(A'_i)=0.375, 其他16人的群体选择概率P(A″_i)=0.5, 结合图2(a)的得益矩阵及式(5)可知, U’ ’ (B₁)=1.3145, U’ ’ (B₂)=2.3855, 假设k=0.5, 则 $P_{B_{1} - B_{2}}$ =0.242, 表示行人M有24.2%的概率模仿违章过街群体的行为, 而有75.8%的概率会坚持选择等待。

3 行人群体从众行为演化的仿真实验及结果分析

图4给出了仿真实验流程。由上述分析可知, 影响过街行人群体演化的因素共有4项, 分别为3类行人在总人群中所占的比例(即行人构成); 违章过街群体占总人群的比例; 参照效应的权重; 噪声参数项。在此假设行人的行为选择都近似于理性行为, 因此将噪声参数项设定为0.5, 取参照效应的权重为0.25。本文主要分析前两项影响因素对群体行为演化的影响。

	Figure Option View Download New Window
	图4 仿真流程图Fig.4 Flow chart of simulation

3.1 行人构成的影响

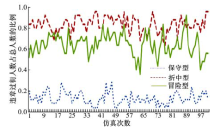
为观察行人构成的影响途经, 将P(A_i)设为常数, 在此设定P(A₁)=0.5。在此设置保守型(S型)、折中型(Z型)、冒险型(X型)行人在总人群中所占的比例, 分析不同群体构成下群体行为的演化过程, 其仿真结果如图5所示。

	Figure Option View Download New Window
	图5 群体构成对群体行为演化的影响效果Fig.5 Effects on evolution of pedestrian constitute

从仿真结果来看, 仿真结果与博弈进化理论的分析结果相符。当有50%左右的人群为保守型时, 总体的闯灯过街比例会降低到30%以内; 当有50%左右的人群是冒险型时, 闯灯比例极具增加, 占总人群80%以上; 当有50%左右的人群为折中型时, 选择过街人群的比例介于30%~70%。仿真结果表明, 冒险型人群居多时, 从众效应会带动更多的人选择闯灯过街, 而保守型居多时闯灯人数则降低。

	Figure Option View Download New Window
	图6 违章人群对群体行为演化的影响效果Fig.6 Effects on evolution of illegally crossing crowd

3.2 违章过街群体占总人群比例的影响

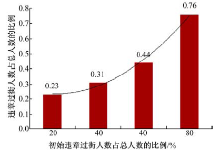
将3种类型人群的比例设置为各占三分之一, 观察初始违章过街人群的比例对群体行为演化的影响。在此选择4个具有代表性的场景进行仿真, $\begin{matrix} P (A_{1}) \end{matrix}$ 分别取值为1/5、2/5、3/5、4/5, 观察在上述4种情况下行为演化的差异性, 共进行了100次仿真, 取其平均值, 结果如图6所示。结果表明, 初始状态下选择违章人群的数量对整个过街人群行为的演化有显著的影响, 从众效应会使得整个人群的演化朝向选择人数较多的结果发展。

4 考虑从众效应的行人社会力仿真模型的改进策略

社会力模型以牛顿力学原理为基础, 将环境中的行人运动描述为受自驱力、行人间相互作用力、行人与障碍物相互作用力的结果。Moussaid等^[8]根据同伴群行人出行的特点, 构建了同伴群作用力, 描述同伴群行人的相互作用。同伴群作用力主要包括了视觉力、聚合力及排斥力。受从众心理影响的过街群体之间形成了结伴关系, 尤其是具有相同决策的群体, 例如违章过街, 在闯灯过街过程中这种结伴关系尤其明显。因此, 可参照同伴群的表达方法, 构建考虑从众因素的行人仿真模型, 并将由于从众产生了行人间的作用力称之为从众力 $\begin{matrix} {\bar{f}}_{B_{1} - B_{2}}^{conf}, \end{matrix}$ 其表达方式如下:

$\begin{matrix} {\bar{f}}_{B_{1} - B_{2}}^{conf} = β {\bar{U}}_{B_{1} - B_{2}} f (P_{B_{1} - B_{2}}, P) \end{matrix}$ (6)

式中: ${\bar{f}}_{B_{1} - B_{2}}^{conf}$ 为行人由B₁ 向邻接的B₂ 靠拢的从众力; β 为模型参数, 描述行人个体之间的吸引强度; ${\bar{U}}_{B_{1} - B_{2}}$ 为单位矢量, 方向从行人B₁ 指向邻接的行人B₂; $P_{B_{1} - B_{2}}$ 概率函数, 由式(4)求得; P为阈值, 例如0.5; $f (P_{B_{1} - B_{2}}, P)$ 为分段函数, 其表达式为:

$\begin{matrix} f = \{\begin{matrix} 0, P_{B_{1} - B_{2}} < P \\ 1, P_{B_{1} - B_{2}} > P \end{matrix} \end{matrix}$

5 结束语

针对“ 中国式过马路” 存在的安全隐患, 以行人过街的从众效应为研究对象, 构建行人过街的演化博弈模型, 并通过仿真实验分析了从众效应对行人过街的影响途径。本文研究结果可为行人仿真模型参数的设置提供参考, 但还存在以下不足:由于从众行为不宜量化, 因此在仿真过程中采用随机数的策略模拟行人的最终决策, 从而使得结果与真实的行为之间存在偏差。因此, 仿真结果只反应了受从众效应影响的行人群体行为的演化趋势。基于第4节的分析结果, 将从众效应应用于行人社会力仿真模型并进行行人群体过街的仿真实验是下一步需要完善的地方。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Brock W, Durlauf S. Discrete choice with social interactions[J]. Review of Economic Studies, 2001, 68(9): 235-260. [本文引用:1]
[2]	Rosenbloom J, Crossing at a red light: behaviour of individuals and groups[J]. Transportation Research, Part F, 2009, 55(4): 389-394. [本文引用:1]
[3]	Han Qi, Arentze T A, Timmermans H. The effects of social networks on choice set dynamics: results of numerical simulation using an agent-based approach[J]. Transportation Research Part A, 2011, 45(4): 310-322. [本文引用:1]
[4]	Ronald N, Arentze T A, Timmermans H. Modeling social interactions between individuals for joint activity scheduling[J]. Transportation Research Part B, 2011, 46(2): 276-290. [本文引用:1]
[5]	Zhou R G, Horrey W J. Predicting adolescent pedestrians' behavioral intentions to follow the masses in risky crossing situations[J]. Transportation Research Part F, 2010, 13(3): 153-163. [本文引用:1]
[6]	吴文静, 罗清玉, 贾洪飞. 参照群体对行人从众过街行为决策的影响[J]. 华南理工大学学报: 自然科学版, 2015, 43(4): 15-19. Wu Wen-jing, Luo Qing-yu, Jia Hong-fei. Effect of reference group on decision of conformity crossing behaviors of pedestrians[J]. Journal of South China University of Technology(Natural Science Editon), 2015, 43(4): 15-19. [本文引用:1]
[7]	Brian S. Dynamics of conformist bias[J]. The Monist, 2005, 88(2): 260-269. [本文引用:1]
[8]	Moussaid M, Perozo N, Garnier S, et al. The walking behavior of pedestrian social groups and its impact on crowd dynamics[J]. Plos One, 2010, 5(4): el0047. [本文引用:1]

2001

0.0

... 在不确定交通环境下,从众效应伴随着行人过街行为决策的全过程^[1] ...

2009

0.0

... 过街行人之间的行为决策存在相互作用关系,因此行人往往会偏离自己原先的选择而做出符合群体行为偏好的决策^[2] ...

2011

0.0

... 考虑社会环境对行为决策的影响已有一些研究文献,例如Han等^[3]建立了社会网络影响下的出行者选择集合动态更新的学习模型,并运用于购物地点选择行为的研究 ...

2011

0.0

... Ronald等^[4]研究了社会网络成员间的信息交流对出行者认知与知识更新过程的影响,并运用于出行计划以及出行地点选择等行为的研究 ...

2010

0.0

... Zhou等^[5]分析了中国行人在与他人过街行为一致以及不一致两种情况下的行人的主观规范和行为控制,并提出了行为干预对策 ...

2015

0.0

. 2015, 43(4):15-19 DOI:doi:10.3969/j.issn.1000-565X.2015.04.003

Effect of reference group on decision of conformity crossing behaviors of pedestrians

参照群体对行人从众过街行为决策的影响

Wu Wen-jing , Luo Qing-yu , Jia Hong-fei.

吴文静, 罗清玉, 贾洪飞

摘　要：从众过街是行人交通的重要安全隐患。在不确定交通环境下，群体参照效应伴随着行人过街行为决策的全过程。文中从行人过街行为的影响因素出发，基于动态博弈理论推演参照群体影响下的行人从众通过或等待的行为变化过程，构建行人过街行为的阈值模型，定量评估参照群体对行人行为决策的影响程度，探讨参照群体与个体行为的相互作用关系，并以某一交叉口为例进行了实证分析。研究结果表明，群体参照效应对行人过街行为决策存在显著影响。研究结果能够丰富和扩展行人行为研究的理论框架和分析方法，为制定、实施行人过街交通的安全管理策略提供科学的决策支持。

... 吴文静等^[6]基于博弈理论分析了参照群体对行人从众过街行为决策的影响 ...

2005

0.0

... 2 从众效应量化前者是假设M完全不知道其他人的行为决策,但是在现实情况下,过街行人M能够随时观察到其他行人的行为变化,并且受到从众心理的影响,随着过街行人 P(Ai)的变化,行人M的期望得益会发生偏差,在此用从众效用ComformistValue表示,且将其重要程度用权重 c表示,则期望得益修改为^[7]: ...

2010

0.0

... Moussaid等^[8]根据同伴群行人出行的特点,构建了同伴群作用力,描述同伴群行人的相互作用 ...