作者简介:刘程(1985-),男,博士研究生.研究方向:汽车传动系统NVH分析与优化.E-mail:liucheng14@mails.jlu.edu.cn
有限元法是预测汽车驱动桥准双曲面齿轮齿根弯曲应力的重要方法,但单独准双曲面齿轮有限元模型约束条件难以确定,为此本文建立了基于整体驱动模型准双曲面齿轮齿根弯曲应力有限元分析模型,并对齿根应力仿真结果与台架试验进行了对比。选用ABAQUS/Standard建立了驱动桥准双曲面齿轮静态啮合模型,仿真结果表明:本文研究的整体驱动桥准双曲面齿轮在啮合过程中小齿轮齿根弯曲应力在靠近大端出现最大值,齿根部位先受到压应力,再受到拉应力;大齿轮齿根弯曲应力在靠近小端出现最大值,齿根部位先受到拉应力,再受到压应力。最后,搭建了驱动桥静扭试验台,并对驱动桥大齿轮齿根弯曲应力进行测量,将台架试验与仿真结果进行了对比分析,对比结果表明,所建立的有限元模型准确可靠,可将此建模方法应用于类似的齿轮齿根弯曲应力分析。
FEM is an important method to predict the tooth root bending stress of driving axle hypoid gear of automobile. However, it is difficult to accurately determine the constraint condition of the FEM model. To solve this problem, a finite element analysis method of hypoid gear tooth root bending stress based on the whole drive axle model is established. Simulation results of obtained from the proposed method are compared with that of rig test. ABAQUS/Standard software is used to establish the static state engagement model of hypoid gears of the driving axle. Results show that, while hypoid gears of the driving axle are meshing, the maximum bending stress of the pinion appears near the heal; the tooth roots bear the comprehensive stress first, then shift to tensile stress. On the contrary, the maximum bending stress of the big gear appears near the toe; the tooth roots bear the tensile stress first, then shift to comprehensive stress. Finally, the gear tooth root bending stress was measured on a driving axle static torsional test rig. Comparison of the test and simulation results demonstrates that the proposed FEM model is reliable and such modeling method can be applied to similar analysis of gear tooth root bending stress.
螺旋锥齿轮和准双曲面齿轮广泛应用于轿车、重型卡车、矿用车驱动桥以及航空飞机变速器等传动系统的动力传递, 它是当前交错轴或者非交错轴之间应用最为广泛的动力传递方式之一。准双曲面齿轮与螺旋锥齿轮主要区别为, 螺旋锥齿轮是两个旋转轴相互交错, 准双曲面齿轮是旋转轴不交错并且有一定的偏置距。准双曲面齿轮的设计与传动系统其他部件的设计一样, 需要提高其可靠性、耐久性、功率密度(功率与质量之比)、动力传递效率, 同时降低制造成本、噪声等。但对于这些复杂的, 看似相互矛盾的齿轮设计要求, 传统的公式设计方法不能满足, 因此, 需要利用先进计算机建模方法, 在齿轮设计阶段综合考虑设计要求。在齿轮众多设计要求中, 可靠性尤为重要。齿轮的失效主要有两种形式, 一种是接触疲劳失效, 这种失效形式主要与齿轮的润滑状态、载荷以及齿面的参数有关; 另一种是齿轮弯曲疲劳失效, 当一个轮齿断裂, 则整个动力传输立刻中断, 此类失效形式比接触失效更为灾难性, 齿轮弯曲疲劳失效与轮齿啮合过程中齿根部位的应力状态直接相关[1]。
不同类型的齿轮在齿根位置的应力状态完全不同。直齿渐开线齿轮在啮合过程中, 齿轮受到单轴拉压应力, 而准双曲面齿轮由于在啮合过程啮合位置和啮合力方向逐渐变化, 因此, 啮合过程中齿根经历更为复杂的多轴应力状态[1], 此类齿轮空间结构复杂, 当前制造和生产过程中仍然面临着诸多难题[2, 3]。目前, 国内外齿轮齿根弯曲应力研究大多集中在平行轴式齿轮、斜齿轮等, 而对准双曲面齿轮的研究主要是考虑单个轮齿或者多个齿轮[2, 3, 4, 5, 6], Handschuh等[3]建立了螺旋锥齿轮三个轮齿对的有限元模型, 并将一个轮齿边缘固定, 另外一个轮齿施加转矩。Litvin等[4]建立了整个齿胚的有限元模型, 模型约束方式与文献[3]类似。唐进元等[2]建立了整个齿胚的有限元模型, 并对轮齿接触进行动力学分析, 在小齿轮施加转速, 大齿轮施加转矩。以上有限元建模过程中在大小齿轮或者轮齿上进行人为的边界约束, 并在一个确定的位置上加载扭矩来预测齿根部位的应力。这种方法主要有两点不足, 第一, 必须在齿轮或者轮齿上定义边界条件去模拟整个齿轮; 第二, 必须确定齿轮力的加载方式。而实际的准双曲面齿轮啮合过程中受到半轴、驱动桥以及轴承变形的影响, 简单的集中力转速施加在齿轮或者轮齿并不能反映实际的应力状态。随着计算机性能的提高, 已有学者[7, 8, 9]建立了驱动桥整体有限元模型, 将阻力矩和转速分别直接加载在驱动桥输入端和输出端上, 并研究各部件之间的相互作用关系, 表明整体驱动桥有限元模型能够更好地模拟实际驱动桥的工况, 但对准双曲面齿轮啮合过程中准双曲面齿轮齿根弯曲应力详细研究较少。
齿轮在啮合过程中具有大转角的几何非线性以及接触非线性, 使得齿轮啮合过程中具有很强的非线性, 不能通过建立简单的数学模型来模拟齿轮非线性啮合过程, 当前应用比较多的是利用有限元方法进行齿轮啮合分析[4, 5, 6, 7, 8, 9]。齿根弯曲应力有限元分析主要分为静态有限元分析[2, 4]和动态有限元分析[8]。文献[3]研究表明, 准双曲面齿轮啮合过程中齿轮啮合速度对齿根弯曲应力的影响不大, 齿轮静态啮合过程中齿根弯曲应力的变化可以反映齿轮在实际运行过程中齿根弯曲应力的变化规律。在准双曲面齿轮有限元建模过程中, 由于齿轮空间结构复杂, 极易导致有限元网格严重扭曲, 使得有限元分析过程不收敛或者计算值不准确。当前, 准双曲面齿轮静态有限元啮合分析方法主要有两类:第一类, 将一个齿轮固定, 另一个齿轮加载载荷[4]; 第二类, 将一个齿轮固定, 另一个齿轮加载, 接着将齿轮旋转一个小角度, 将一个齿轮固定, 另一个齿轮加载, 依此类推, 得到齿轮轮齿在一个啮合循环过程中齿根应力变化情况[2]。以上齿轮齿根弯曲应力分析方法不能得到轮齿啮合过程中啮合应力连续变化。因此, 建立真实反映准双曲面齿轮啮合过程的整体驱动桥静态有限元模型具有重要意义。
本文以某汽车整体后驱动桥为研究对象, 建立了整体驱动桥有限元模型, 利用ABAQUS/Standard静态通用求解器对准双曲面齿轮多齿接触的非线性啮合过程进行模拟, 得到齿轮齿根部位应力变化规律, 并将数值仿真结果与试验结果进行了对比分析。
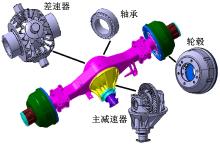
要建立驱动桥高精度的整体有限元模型, 首先需要建立汽车驱动桥整体几何模型, 汽车驱动桥组成见图1, 包括主减速器, 差速器, 半轴, 轮毂, 桥壳, 差速器壳, 主减速壳体及支持轴承等部件。其中, 大部分部件可根据零件图纸直接在CATIA中建立三维数字模型, 但由于主减速器中准双曲面齿轮的轮齿齿面为空间复杂曲面[4, 10], 因而通过三维建模软件直接建模非常困难。
对于准双曲面齿轮齿面的建模方法, 国内外有很多学者进行了研究[11, 12, 13, 14, 15, 16], 准双曲面齿轮加工方法主要分为成形法(Formate)或者展成法(Generate)对轮齿进行切割, 并利用端面铣刀(Face-milling)或者端面滚刀(Face-hobbing)加工方法进行齿轮加工, 当前应用最为广泛的是利用端面铣刀法(FM)加工的格林森(Gleason)制准双曲面齿轮。随着数控机床(CNC)[12, 13, 14]的发展, 为了减小齿轮在啮合过程中的振动噪声, 改善齿轮的啮合润滑条件, 利用刀倾法(Tilt)以及变性法(Modified-roll)分别对刀具轮廓进行设计和增加摇台自由度, 从而对齿轮轮廓进行修饰。目前, 格林森制准双曲面齿轮加工方法主要分为[15]HF(G)T(Hypoid gear formate/generate tilt), HF(G)M(Hypoid gear formate/generate modified roll), 由于刀倾法HF(G)T只需在原来机床的基础上重新设计刀具轮廓, 因而得到了广泛应用。HGT在利用展成法加工工件过程中, 工件与摇台一起旋转, HFT在利用成形法加工齿轮过程中, 摇台固定, 可看作展成法的一种特殊情况。汽车用准双曲面齿轮中, 一般地, 当大轮锥角较大时既可以采用成形法加工, 也可以采用展成法加工; 当大轮锥角较小时必须采用展成法加工, 小轮采用展成法加工。本文所研究的齿轮采用格林森制展成法加工小齿轮, 成形法加工大齿轮, 从上面分析可知, 成形法加工是展成法特例, 本文只列出基于展成法齿面建模方法。
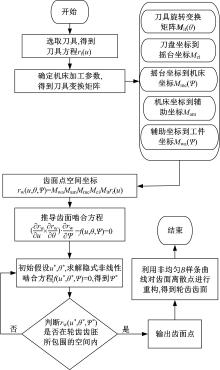
HFT齿面建模中应用最多的是基于Litvin等[16]提出的共轭曲面法。Litvin通过研究准双曲面齿轮的生产过程, 将齿轮加工过程中刀具旋转运动产生的点通过空间变换得到齿轮面上的点。由于利用Litvin提出的方法得到齿轮面的点为有限离散的数据点, 为生成高精度的齿轮面, 需要对其进行插值[10]。齿轮面精确建模方法的具体构建流程见图2, 图中u、θ 为刀具旋转所形成齿面参数, ψ 为齿胚旋转角度。建模过程描述如下:根据刀具参数得到刀具坐标矢量; 对上述矢量进行坐标变换得到刀具所形成曲面; 根据机床参数将刀具曲面变换到齿轮坐标系中, 根据准双曲面齿轮啮合原理得到啮合方程; 根据轮齿面上点必须在轮齿齿胚上, 得到轮齿齿面离散点; 对这些离散点利用非均匀B样条曲线(NURBS)进行重构[10], 得到准双曲面大小齿轮三维模型, 如图3所示, 对建立的三维零件按照图纸在CATIA中进行装配, 利用DMU装配模型进行运动仿真, 并对各个运动部件之间进行干涉和间隙检查, 得到整体驱动桥三维数字模型。
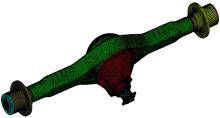
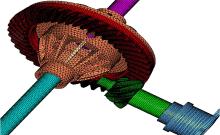
将第1节建立的整体驱动桥保存为* .stp格式, 并导入到专业的网格划分软件Hypermesh中, 本文研究的重点为准双曲面齿轮的啮合, 对导入的几何模型进行几何清理与简化, 对于桥壳、主减速器壳、差速器壳等支持部件采用四面体网格, 对应单元数为259 099个, 节数点77 804个。对主减速器齿轮、差速器齿轮、轴承、半轴、轮毂采用六面体网格, 对应单元数为587 910个, 节数点709 571个, 最后得到整体驱动桥有限元网格如图4所示。图5为主要部件的有限元网格。
有限元分析前处理包括求解器的选择、单元类型的选取、载荷与边界条件的施加等, 这些因素的选取直接决定分析结果的正确性。先进的有限元分析软件ABAQUS在求解齿轮啮合等非线性模型上具有独特的优势, 本文选取ABAQUS/Standard求解器, 对齿轮啮合过程进行静态有限元分析。本文以汽车在某一匀速典型工况下行驶时驱动桥齿轮啮合过程为研究对象, 模拟驱动桥输入端为90.515 rad/s, 驱动桥阻力矩为4678 N· m, 车速为22 km/h本驱动桥整体有限元求解模型的建立主要包括以下关键步骤。
(1)材料属性定义
整体驱动桥主要部件材料的定义如表1所示。
| 表1 驱动桥部件材料属性 Table 1 Material properties of drive axle components |
(2)单元属性定义
在有限元分析过程中, 单元类型的选取非常关键, 不同类型的单元适合不同的分析问题, 直接影响分析结果的精度。根据本文所研究的问题, 六面体单元选用具有沙漏和自锁控制的线性减缩积分的C3D8R, 四面体单元选用修正的二阶的C3D10M。
(3)分析步定义
分析步的定义直接关系到齿轮啮合求解过程, 如果分析步定义不正确会直接导致分析结果错误或者分析过程不收敛而终止, 因此必须慎重定义分析步, 本文选用的是ABAQUS/Standard/static, general分析类型。为保证求解过程的收敛, 定义两个分析步。第一步:载荷加载, 时间长度设置为1, 打开几何非线性, 在自动稳定中选用“ 指定衰减因子” , 其值为0.0001, 勾选“ 使用为应变能设置了最大稳定比例的自适应稳定性” , 其他参数值为默认值。第二步:齿轮啮合旋转, 时间长度设置为0.025, 同样打开几何非线性, 在自稳定性中选用“ 使用前一通用分析步的阻尼因子” , 其他参数与上一分析步相同。
(4)接触定义
为简化模型, 在整个驱动桥中对于螺栓连接处以及不存在相对滑动的接触部位都简化为绑定。轴承滚子与外圈进行绑定, 与内圈建立面面接触。半轴齿轮面与行星齿轮面以及主减速器中主动锥齿轮与被动锥齿轮之间建立面面接触, 需要注意的是, 需要根据齿轮的主动与从动选择主面和从面。设置接触属性中的切向行为中摩擦因数为0.1, 法向行为为“ 硬” 接触, 其他参数为默认设置。
(5)边界条件定义
载荷加载分析步中, 固定驱动桥的输入端, 在输出端轮毂上约束除绕自身轴线旋转外的所有自由度, 并在输出端加载4678 N· m行驶阻力, 力矩以斜坡线性加载。在齿轮啮合旋转分析步中, 约束驱动桥输入输出端除绕自身轴线外的所有自由度, 并在输入端输入转角2.26 rad(由啮合旋转时间和啮合转速确定), 同样以斜坡线性加载, 输出端加载瞬态阻力矩, 大小与前一分析步相同。为增加啮合过程的稳定性, 在初始条件中定义主被动齿轮初始速度, 在ABAQUE中, 利用“ 预定义场” 对齿轮的初始啮合速度进行定义, 驱动桥输入旋转速度为90.515 rad/s, 轮毂输出速度为16.84 rad/s。最终建立完成的有限元模型如图6所示。
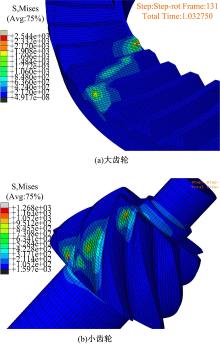
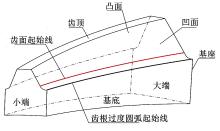
将第2节建立好的模型提交给ABAQUS/Standard求解器, 最后得到有限元分析结果。图7为齿轮啮合过程中大、小齿轮对应的Mise应力。从图中可以看出, 齿面Mise应力在相邻三个轮齿上分布, 理论上, 准双曲面齿轮大小齿轮齿面啮合过程为点接触[16], 但由于齿面弹性变形以及轴承支持变形的影响, 使得齿面出现近似接触椭圆, 为分析轮齿在整个啮合过程中齿根弯曲应力变化规律, 需对齿根位置弯曲应力进一步研究。图8为齿胚轮廓定义, 为了更好地观察, 将单个轮齿圆角过度曲面映射到一个长方形平面上, 长方形长度方向从左到右为轮齿小端到大端, 宽度方向为圆角起始位置(ST)到齿轮接触起始位置(ED)。图9为小齿轮轮齿整个啮合过程中凹面齿根部位瞬时最大主应力变化云图, 为方便显示, 图中从上到下依次选取啮合过程中5个位置, 图中水平轴和竖直轴分别相对于齿宽和齿轮圆角过度处尺寸进行归一化处理。齿轮在啮合过程中啮合线从大端向小端移动, 齿根部位最大主应力也跟随变化, 由于本驱动桥整体模型考虑到桥壳、轴承、主减速器壳等变形对齿轮啮合的影响, 使得在小齿轮进行啮合时, 即小齿轮大端开始接触时达到最大(大约530 MPa), 此点为齿轮啮合过程中小齿轮的危险点。图10为位于小齿轮齿根部位危险点最大主应力位置对应单元的3个主应力变化的时间历程, 从图中可以看出, 齿轮在啮合中占主导地位的是第一主应力和第三主应力, 此处单元在整个啮合过程中先受到压应力(第三主应力), 然后受到拉应力(第一主应力), 如假设在此位置贴上虚拟应变片, 则此处应变片应力变化过程如图11所示。
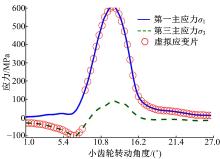 | 图11 小齿轮齿根危险点虚拟应变片应力变化历程Fig.11 Stress changes history of virtual strain gauge at dangerous point for pinion tooth root |
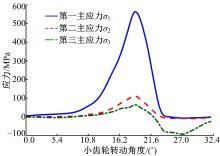
类似可以得到被动齿轮轮齿凸面在整个啮合过程中齿根部位第一主应力变化云图, 如图12所示, 图中从上到下依次选取啮合过程中与小齿轮上述位置相对应的5个位置。从图中可以看出, 由于本驱动桥整体模型考虑到驱动桥其他部件变形的影响, 使得被动齿轮齿根部位最大主应力出现在靠近小端位置, 最大主应力值为600 MPa, 此点为齿轮啮合过程中大齿轮齿根危险点。主被动齿轮最大主应力云图的差异主要是由于齿轮齿面和齿根部位几何形状不同导致的。图13为大齿轮齿根危险点处对应最大第一主应力位置单元在整个啮合过程中对应的第一主应力、第二主应力、第三主应力时间历程。从图中可以看出, 齿轮在啮合过程中第一主应力和第三主应力占主导地位, 齿根部位单元先受到拉应力, 最后受到压应力, 如假设在此位置贴上虚拟应变片, 则此处应变片应力变化过程如图14所示。
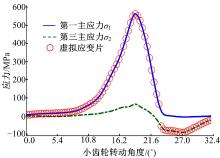 | 图14 大齿轮齿根危险点虚拟应变片应力变化历程Fig.14 Stress changes history of virtual strain gauge at dangerous point for gear tooth root |
对比主被动齿轮在整个啮合过程中齿根部位应力变化规律可以得出, 本文基于整体驱动桥的准双曲面齿轮在啮合过程中由于考虑到整体驱动桥桥壳主减速器、半轴、轴承等部件变形的影响, 使得小齿轮凹面齿根部位在进入啮合时(即齿轮大端)弯曲应力达到最大值, 齿根部位先受到压应力, 再受到拉应力, 大齿轮凸面齿根部位离开啮合时(即齿轮小端)弯曲应力达到最大值, 齿根部位先受到拉应力, 再受到压应力。
对比文献[2]中单独只考虑准双曲面齿轮所得到的轮齿齿根弯曲应力分布可知, 驱动桥准双曲面齿轮在实际加载运行过程中会由于受到驱动桥支撑刚度、主减速器支撑刚度以及驱动桥其他部件的影响, 使得齿轮的啮合与单独考虑准双曲面齿轮啮合时不同, 因此驱动桥齿轮设计时不仅要单独分析准双曲面齿轮的啮合, 而且还需对准双曲面齿轮安装在驱动桥上处于加载状态下进行齿轮的啮合分析。
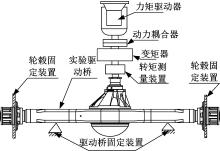
为验本文所建立的有限元模型的精确性, 需要对驱动桥中准双曲面齿轮啮合过程齿根弯曲应力进行测量。本文是基于整个驱动桥主被动齿轮啮合过程的研究, 文献[3]表明, 准双曲面齿轮啮合过程中, 转速对齿轮齿根弯曲应力影响不大, 而且在整体驱动桥布置滑环进行齿根弯曲应力的动态测量是十分困难的。因此, 本文只对驱动桥齿轮静态啮合齿根弯曲应力进行测量。选用如图15所示的CM-2B型静态应变测试系统, 驱动桥静扭试验台架如图16所示, 台架具体试验装置结构如图17所示。试验过程中将轮毂固定, 在小齿轮端加载输入900 N· m扭矩, 利用静态应变仪直接将应变片的电阻变化通过测试系统的USB接口输出到计算机。
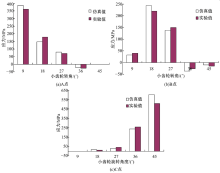
为全面反映大齿轮啮合过程中齿根弯曲应力变化, 对大齿轮齿根位置A、B、C三测点齿根弯曲应力进行测量, 测量点的布置如图18所示, 单对轮齿完成整个啮合过程分成5个位置来计算, 每个位置小轮转动9° , 一共需测量15个位置。将齿轮试验测量值与仿真值相对应位置进行对比, A、B、C三测点的试验与仿真对比如图19所示。从图中可以看出, 仿真结果与试验结果沿A、B、C三点变化趋势基本一致, 最小相对误差在10%以内, 最大相对误差在25%以内, 仿真结果较好, 说明有限元仿真结果可信, 模型建立正确, 可以应用于类似齿轮分析。
(1)建立了基于整体汽车后驱动桥准双曲面齿轮有限拟合模型, 并利用ABAQUS/Standard求解器对有限元模型进行求解。
(2)对驱动桥准双曲面齿轮啮合过程中齿根弯曲应力进行了分析, 结果表明:小齿轮在啮合过程中靠近大端齿根弯曲应力最大, 齿根部位危险点处先受压后受拉; 大齿轮啮合过程中靠近小端齿根弯曲应力最大, 齿根部位危险点处先受拉后压。
(3)驱动桥台架试验与仿真得到的准双曲面大齿轮齿根弯曲应力值对比表明, 本文建立的有限元模型具有较高精度。
(4)通过本文建立的驱动桥准双曲面齿轮齿根应力的预测方法可以全面检查驱动桥准双曲面齿轮在加载时齿轮的啮合, 在驱动桥准双曲面设计时, 可以首先单独考虑准双曲面齿轮啮合, 然后基于整体驱动桥对准双曲面齿轮设计参数进行优化。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|