车-液耦合动力学建模及液体响应成分对操纵性的影响

引用本文

万滢, 赵伟强, 封冉, 凌锦鹏, 宗长富, 郑宏宇. 车-液耦合动力学建模及液体响应成分对操纵性的影响. 2017, 47(2): 353-364
WAN Ying, ZHAO Wei-qiang, FENG Ran, LING Jin-peng, ZONG Chang-fu, ZHENG Hong-yu. Dynamic modeling and vehicle-liquid coupling characteristic analysis for tank trucks. Journal of Jilin University Engineering and Technology Edition, 2017, 47(2): 353-364 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201702003
Permissions

车-液耦合动力学建模及液体响应成分对操纵性的影响

万滢, 赵伟强, 封冉, 凌锦鹏, 宗长富, 郑宏宇

吉林大学汽车仿真与控制国家重点实验室,长春 130022

赵伟强(1977-),男,副教授,博士.研究方向:汽车仿真与控制.E-mail:zwqjlu@163.com

作者简介:万滢(1991-),女,博士研究生.研究方向:重型商用车及液罐车辆的动力学与稳定性控制.E-mail:yingwan12345@163.com

基金项目:国家自然科学基金项目(51575224,51575223),吉林省科技发展计划项目(20150204066GX).

摘要

针对液罐车辆不同工况下车-液耦合动态响应特性及对整车影响的研究少、液体晃动简化建模理论不足的问题,根据描述液体模型的差异,本文结合液体模型和车辆操纵模型建立了4种液罐车辆动力学模型:①等质量刚体模型;②准静态液体模型;③横向等效单摆模型;④数值液体模型。通过对比不同工况类型和不同工况激烈程度下4种模型的响应差异,分析了不同情况下液体晃动各种响应成分被激发的程度及其对车辆操纵响应的影响,从而确定了不同工况时车-液耦合程度,并给出了建立合理简化模型的建议,为建立液体简化模型和进行液罐车稳定性主动控制奠定基础。

关键词: 车辆工程; 车-液耦合; 数值模型; 操纵响应; 晃动特性

中图分类号:U461.6,U469.6 文献标志码:A 文章编号:1671-5497(2017)02-0353-12

Dynamic modeling and vehicle-liquid coupling characteristic analysis for tank trucks

WAN Ying, ZHAO Wei-qiang, FENG Ran, LING Jin-peng, ZONG Chang-fu, ZHENG Hong-yu

State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022,China

Abstract

In order to determine the degree of vehicle-liquid coupling in different conditions, four dynamic models are developed, all of which consist of vehicle handling dynamics model and liquid model. The difference of the four models is in the liquid model: 1, rigid cargo model, 2, quasi-static liquid model, 3, lateral equivalent pendulum model, 4, complicated CFD liquid slosh model. The Under different handling conditions and different intensity, the responses calculated by the four models are compared. The excited degree of various response components of liquid sloshing and its influence on vehicle handling dynamics are analyzed. The results may provide guidance for the development of more suitable simplified model and active stability control of tank vehicles.

Key words: vehicle engineering; vehicle-liquid coupling dynamics; liquid slosh CFD model; vehicle handling response; liquid slosh characteristics

Show Figures

0 引言

液罐车是应用最广泛的液体危险品运输工具。由于罐车载重大、重心高、体积大, 且液体受激励时会产生晃动, 重心不稳, 因此易发生侧翻等失稳事故, 并极易伴随油品爆炸等连续事故。通过罐体优化提高液罐车稳定性方面已有大量研究, 但确定的罐体形状不能同时降低充液比变化、具体工况和失稳方式不同等各种情况下的不稳定性。因此, 通过主动安全控制, 提升液罐车的稳定性, 是一种适用性更广的方式, 但目前针对这方面的研究很少。

对液罐车进一步进行系统稳定性分析, 需要有足够准确性, 且具有封闭形式的液罐车动力学模型; 进一步进行液罐车辆稳定性控制, 则可能需要兼顾准确性和计算速度的简化液罐车模型。目前的液体简化模型主要有准静态模型^[1]和机械力学等效模型^[2](以单摆模型和弹簧-质子模型为主), 准静态模型无法反映液体的动态变化和晃动, 单摆、弹簧-质子等目前的等效力学模型只能反映液体在线性或弱非线性范围内的晃动情况^[3], 对于临近危险工况时可能被激发的非线性特性无法描述, 且现在的液罐车必须安装隔板, 大多隔板带有空洞, 对这种罐体的纵向晃动和纵向液体流动, 目前的机械力学模型还不能描述。关于各类简化模型的准确性, 文献[4]对比了半解析的横向液体晃动模型、刚体模型和准静态模型分别与侧翻静平衡方程结合求解得到的侧翻阈值, 发现动态阈值远小于准静态阈值, 准静态阈值远小于刚体货物阈值, 且动态模型比准静态的阈值降低高达50%; 文献[5]搭建了缩比液罐车实验装置, 用于对比不同液罐车模型与实验测试结果之间的差别, 结果发现刚体模型会严重低估侧向力/力矩, 分布摆动态模型和准静态模型或低估或高估, 随着工况不同而变化, 即工况不同会导致模型准确性不同, 且充液比和车速增加带来的误差增大, 原因是液体的非线性特征越来越明显。

要建立能够用于系统分析或整车稳定性控制的液罐车模型, 首先需要对液罐车辆的响应特性进行充分分析, 并确定需要考虑的因素。分析液罐车响应特性方面的研究不少, 但大多局限于以下两个方面:①结合简化液体模型(主要为准静态^[6]或单摆模型^{[7, 8, 9]}, 或在准静态基础上引入瞬态峰值系数^[10])和车辆模型(车辆模型或为临界方程, 或为动态方程), 分析侧翻临界车速、整车响应特性、液体倾角和液体晃动等对整车响应的影响, 但由于目前的简化液体模型不能充分反映液体的动力学特性, 因此获得的分析结果的准确性和指导意义有限; ②基于流体CFD软件建立罐内液体数值模型, 分析简单激励下液体晃动力和晃动力矩及其受充液比、罐体形状等的影响^{[11, 12]}, 没有考虑实际工况和车辆动力学带来的复杂激励, 且无法给出液体特性对车辆响应的影响。极少数研究结合数值液体模型和车辆模型分析液罐车辆的响应^{[13, 14]}。文献[15]结合三维液体FLUENT模型和5DOF半挂车模型, 对半挂液罐车进行了阶跃转向和双移线工况的仿真并与固体货物对比, 结果表明由于液体与车的相互影响, 双移线工况中侧倾角的第二峰值比第一峰值高(在固体货物中, 第二峰值并不能看出比第一峰值高)。文献[16]利用Pasimodo软件中的液体/颗粒模型结合Simpack软件中的17DOF卡车模型实现联合仿真, 发现双移线工况中液体/颗粒货物簧载质量的侧倾运动相比刚体货物更低, 说明颗粒物体/液体的横向运动对车辆行驶稳定性的影响可能是积极的。以上基于复杂液罐车辆模型, 对液罐车响应特性的分析结果非常有限, 但得到的结论充分说明了考虑复杂液体晃动和与车辆模型的结合, 对分析液罐车响应特性的重要性。

液体晃动运动的响应成分包括:惯性响应、液面倾斜、主频动态晃动以及高阶非线性动态晃动。刚体模型、准静态模型、等效模型和数值晃动模型的区别, 本质上是对液体响应成分考虑的不同:①刚体模型只考虑了惯性力的影响; ②准静态模型同时考虑了惯性力和液面倾角的影响; ③等效模型考虑了惯性力、液面倾角以及动态晃动的影响; ④数值晃动模型考虑了惯性力、液面倾角、动态晃动以及高阶晃动等非线性成分的影响。

因此, 基于不同液体模型的液罐车模型的准确性的不同, 实质是液体晃动各种响应成分被激发的程度及其对车辆操纵响应影响的不同。

由于工况的类型、激烈程度、充液比、不同模型的准确性都不相同, 所以需要对不同工况类型和不同激烈程度的液罐车响应进行分析, 确定不同情况下液体晃动各种动力学特性被激发的程度及其对车辆操纵响应影响大小, 才能建立合理的简化模型, 做到在不同情况下既能准确反映液罐车的动态特性又能保证计算能力, 为进行液罐车稳定性主动控制奠定基础。

针对目前液罐车辆响应特性分析的不足, 建立的简化模型理论不足、缺乏指导的问题, 本文首先建立了四种液罐车模型, 包括基于液体数值模型和车辆模型的双向耦合液罐车模型, 等质量刚体货物车辆模型、基于准静态液体的液罐车模型和基于单摆等效模型的液罐车模型, 通过合理安排工况类型和工况的激烈程度, 对比四种液罐车模型的响应, 确定不同工况对各种液体特性的激发程度以及各液体特性对车辆响应的影响大小, 并基于分析结果对建立简化液罐车模型给出了一些建议。

1 液罐车辆操纵动力学数学模型

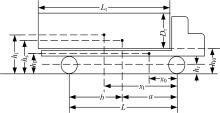
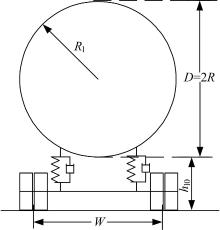
液罐车辆的响应与车辆形式、液罐形状、装载量等都有关系。本文研究对象为有前、后两个车轴的单车液罐车, 前轴每侧为单胎, 后轴每侧双胎, 液罐为圆柱形。运载介质为煤油, 考虑50%充液比。车辆的侧视图和后视图如图1、图2所示, 设计的整车参数如表1所示。

	Figure Option View Download New Window
	图1 整车右视图Fig.1 Vehicle model-right view

	Figure Option View Download New Window
	图2 整车后视图Fig.2 Vehicle model-rear view

本文考察液罐车辆操纵稳定性, 需要考虑车辆侧向、横摆和侧倾三个自由度, 并要考虑垂直载荷对轮胎力的影响, 因此作如下假设:①前进速度恒定, 各车轮无驱动和制动力; ②车体无俯仰运动和纯垂向运动; ③暂不考虑前后轴的质量、侧倾和垂向运动; ④路面平坦。

表1 整车参数 Table 1 Tank truck parameters

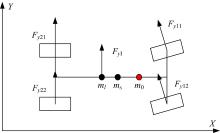
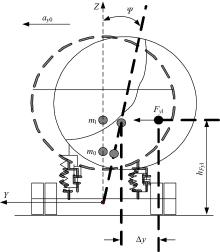
	Figure Option View Download New Window
	图3 液罐车车体部分受力图-俯视Fig.3 Body part of tank truck-top view

对于整车m_s, 将液体m_l与车体m₀分隔, 则液体与车体相互之间的影响全部由相互作用力和力矩来表示。液体对车体的侧向力由惯性和冲击两个方面导致。车体部分受力如图3和图4所示。

	Figure Option View Download New Window
	图4 液罐车车体部分受力图-后视Fig.4 Body part of tank truck-rear view

整车质心m_s处的运动为:纵向速度u_c, 侧向速度v, 横摆角速度r, 侧倾角加速度 $\begin{matrix} \overset{\cdot \cdot}{φ} \end{matrix}$ 。

从而, m₀质心处的侧向加速度为:

$\begin{matrix} a_{y 0} = \overset{\cdot}{v} + u_{c} r + (a - x_{0}) \overset{\cdot}{r} - (h_{0} - h_{r}) \overset{\cdot \cdot}{φ} \end{matrix}$ (1)

液体货物m_l质心处的侧向加速度:

$\begin{matrix} a_{yl} = \overset{\cdot}{v} + u_{c} r - (x_{l} - a) \overset{\cdot}{r} - (h_{l} - h_{r}) \overset{\cdot \cdot}{φ} \end{matrix}$ （2）

根据达朗贝尔原理, 对车辆车体部分m₀建立动力学平衡方程。

m₀质心处的侧向运动平衡方程:

$\begin{matrix} m_{0} [\overset{\cdot}{v} + u_{c} r + (a - x_{0}) \overset{\cdot}{r}] - m_{0} (h_{0} - h_{r}) \overset{\cdot \cdot}{φ} = F_{yf} + F_{yr} + F_{yl} \end{matrix}$ (3)

m₀质心处的横摆运动平衡方程:

$\begin{matrix} I_{zz 0} \overset{\cdot}{r} + m_{0} (a - x_{0}) a_{y 0} = a F_{yf} - b F_{yr} - (x_{l} - a) F_{yl} - I_{zzl} \overset{\cdot}{r} \end{matrix}$ （4）

簧载质量m₀部分的侧倾平衡:

$\begin{matrix} I_{xx 0} \overset{\cdot \cdot}{φ} - m_{0} (h_{0} - h_{r}) a_{y 0} = m_{0} g (h_{0} - h_{r}) φ + m_{l} g (h_{l} - h_{r}) φ - I_{xxl} \overset{\cdot \cdot}{φ} + F_{yl} (h_{Fyl} - h_{r}) + m_{l} gΔy - C_{s} \overset{\cdot}{φ} - K_{s} φ \end{matrix}$ (5)

式中:F_y_l、h_Fy_l、Δ y分别为液体对车体的侧向力、侧向力作用点距地面距离、液体由于晃动导致质心偏离轴线的横向距离。

此外, F_y_f、F_y_r分别为前轴和后轴总的侧向力, 计算公式如下:

$F_{yf} = F_{y 11} + F_{y 12} = α_{f} (C_{α 11} + C_{α 12}) = (\frac{v + ar}{u_{c}} - δ_{f}) (C_{α 11} + C_{α 12})$ （6）

$\begin{matrix} F_{yr} = F_{y 21} + F_{y 22} = α_{r} (C_{α 21} + C_{α 22}) = \frac{v - br}{u_{c}} (C_{α 21} + C_{α 22}) \end{matrix}$ （7）

式中:C_α₁₁、C_α₁₂、C_α₂₁、C_α₂₂分别为4个轮的侧偏刚度, 考虑到随着垂直载荷的变化, 侧偏刚度也变化, 因此采用查表法, 侧偏刚度随垂直载荷变化而变化。

2 液罐车动力学模型的实现

前文中建立的液罐车辆操纵数学模型, 将车辆刚体部分和液体货物部分隔开, 并以相互作用力/力矩进行联系, 液体货物对车辆的作用力/力矩需要用一定的液体模型来求解。

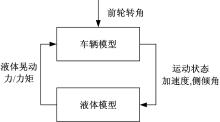
本文采用等质量刚体、准静态液体、横向等效单摆模型和横向二维液体数值模型来求解液体对车辆的晃动力/力矩, 车辆模型和液体模型之间的交互关系如图5所示, 液体模型根据车辆模型求得的当前运动状态, 以此作为激励求得对车辆的作用力/力矩, 车辆模型根据前文所述的数学模型, 以驾驶员操纵和液体作用力/力矩为输入求得下一时刻的车辆状态。

	Figure Option View Download New Window
	图5 车辆模型与液体模型交互示意图Fig.5 Simulation scheme for vehicle-fluid interaction

2.1 基于等质量刚体的模型

刚体模型的特点是液体完全以刚体货物的特点来考虑, 没有冲击也没有流动引起的载荷转移, 则F_y_l、h_Fy_l、Δ y分别为:

$\begin{matrix} \{\begin{matrix} F_{yl} = - m_{l} a_{yl} = \\ - m_{l} [\overset{\cdot}{v} + u_{c} r - (x_{l} - a) \overset{\cdot}{r} - (h_{l} - h_{r}) \overset{\cdot \cdot}{φ}] \\ h_{Fyl} = h_{l} \\ Δy = 0 \end{matrix} \end{matrix}$ (8)

带入并整理, 简化为如下完全考虑整车m_s质心处的动力学方程组:

$m_{s} (\overset{\cdot}{v} + u_{c} r) - m_{s} (h_{s} - h_{r}) \overset{\cdot \cdot}{φ} = F_{yf} + F_{yr}$ （9）

$I_{zz} \overset{\cdot}{r} - I_{xz} \overset{\cdot \cdot}{φ} = a F_{yf} - b F_{yr}$ （10）

$\begin{matrix} I_{xx} \overset{\cdot \cdot}{φ} + C_{s} \overset{\cdot}{φ} + [K_{s} - m_{s} g (h_{s} - h_{r})] φ = m_{s} (h_{s} - h_{r}) (\overset{\cdot}{v} + u_{c} r) + I_{xz} \overset{\cdot}{r} \end{matrix}$ (11)

2.2 基于准静态液体的模型

准静态模型只考虑受到加速度作用时稳态液面倾角变化产生的载荷转移, 不考虑液体动态晃动, 液体晃动自由表面被假设始终为平面。

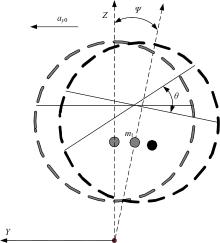
	Figure Option View Download New Window
	图6 准静态液面倾角Fig.6 Free surface of quasi-static liquid model

在液体质心处的侧向加速度和侧倾角的作用下产生的液面倾角如图6所示, 大小为:

$\begin{matrix} θ = \arctan (a_{yl} / g) + φ \end{matrix}$ （12）

从而产生的额外质心侧向转移量为:

$\begin{matrix} Δy = [R_{l} - (h_{l} - h_{l 0})] sinθ \end{matrix}$ （13）

以及作用力和作用点为:

$\begin{matrix} \{\begin{matrix} F_{yl} = - m_{l} [\overset{\cdot}{v} + u_{c} r + (a - x_{l}) \overset{\cdot}{r} + (h_{l} - h_{r}) \overset{\cdot \cdot}{φ}] \\ h_{Fyl} = h_{l} \end{matrix} \end{matrix}$ （14）

2.3 基于等效单摆的模型

一般工程应用当中, 为保证模型计算的实时性, 将小幅晃动问题等效为线性等效力学模型, 使等效系统与相应阶的晃动具有相同力学特性。本文采用钟摆阻尼器类比液体的晃动, 研究表明钟摆等效模型能相对更有效地体现液体横向激励晃动特征。

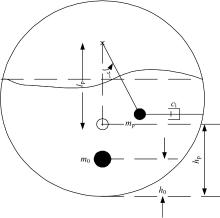
钟摆模型等效示意图如图7所示。全部的液体质量m_l分为两个部分:不参与晃动的固定质量m_l0, 和等效钟摆质量m_p, 在激励作用下, 固定质量m_l0固定在罐体上与罐体一同运动, 钟摆质量m_p除罐体运动外还有单摆运动, 并具有一定的阻尼特性。等效单摆模型涉及到的参数包括以下几个:固定质量m_l0, 固定质量至罐底的距离h₀, 单摆质量m_p, 单摆质子静平衡时至罐底的距离h_p, 摆长l_p, 单摆阻尼c_l。

	Figure Option View Download New Window
	图7 钟摆阻尼模型示意图Fig.7 Equivalent pendulum damping model

基于以下等效原则, 确定等效单摆模型的参数:①液体总质量不变; ②质心位置一致; ③液体晃动基频与等效系统固有频率相等; ④液体晃动产生的作用力和力矩与等效系统形成的作用力/力矩相等; ⑤液体系统动能与等效系统动能相等。

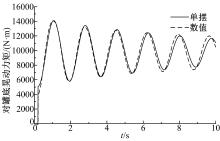
本文对50%充液比的情况进行了辨识, 得到等效单摆模型的参数如下:m_l0=2152.36 kg; h_l0=1.181 m; m_p=2748.5 kg; h_p=0.1012 kg; l_p=0.7529 kg; c_l=524 kg/(m· s^-1)。参数辨识时, 采用1 m/s²加速度激励, 辨识完成后采用2 m/s²加速度激励, 等效单摆模型和数值模型获得的对罐底的侧倾力矩对比如图8所示, 由图8可知, 所建立的等效模型在合理加速度范围内可准确表征液体晃动力/力矩。

	Figure Option View Download New Window
	图8 液体晃动力矩对比Fig.8 Comparison of liquid slosh momentum

2.4 基于数值液体模型的双向耦合模型

在MATLAB/Simulink中建立车辆模型, 在FLUENT流体计算软件中建立液体晃动模型。

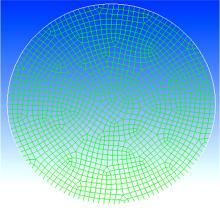
首先, 在FLUENT中建立横向二维液体晃动模型, 罐体截面为圆形, 二维网格如图9所示。采用VOF二相流模型捕捉自由液面, 采用k-ε 湍流模型,

	Figure Option View Download New Window
	图9 FLUENT数值模型液体网格Fig.9 Generated mesh for fluid dynamics analysis

并采用非迭代时间推进法NITA提高计算精度和收敛速度。

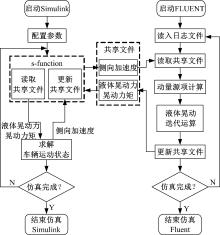
MATLAB与FLUENT没有直接的联合仿真接口, 但MATLAB/Simulink可读写数据文件, FLUENT可采用日志文件进行自动设置和运算, 并可通过编写基于c语言基础的UDF函数实现对数据文件的读写, MATLAB/Simulink和FLUENT之间实现并行协同仿真的过程如图10所示。

	Figure Option View Download New Window
	图10 并行协同仿真流程图Fig.10 Flow chart of parallel collaborative simulation

3 仿真分析

为了能够确定不同工况下各种液体特性的激发程度以及各液体特性对车辆响应的影响大小, 本文采用三种仿真工况进行分析:阶跃转向, 正弦, 双移线。阶跃转向工况体现开环稳态特性, 正弦工况体现开环动态特性, 双移线工况是标准操稳工况, 同时也是闭环工况, 能够体现不同货物特点对操纵稳定性的影响。

对于各工况, 为分析各液体响应成分的激发程度, 及其对车辆操纵动力学的影响, 仿真分析时考察液体单摆模型和数值模型计算的侧向晃动力和晃动力矩, 以及液罐车的横摆角速度、侧向加速度、质心侧偏角、侧倾角, 对于侧翻稳定性考察广泛使用的指标:横向载荷转移率LTR, 其计算公式如下:

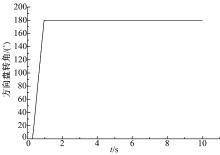
$\begin{matrix} LTR = |\frac{F_{zl} - F_{zr}}{F_{zl} + F_{zr}}| \in [0, 1] \end{matrix}$ （15）

3.1 阶跃转向工况

阶跃转向工况方向盘转角180° , 转向系统传动比25, 方向盘转角增大时间为0.66 s, 如图11所示。

	Figure Option View Download New Window
	图11 阶跃工况-方向盘转角Fig.11 Step momoeuvre-steering wheel angle input

仿真分析中, 单摆模型计算结果在72 km/h发生侧翻, 因此考虑40~70 km/h的情况。通过对比不同车速、不同模型计算结果, 发现:

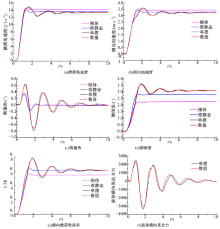
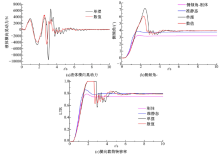
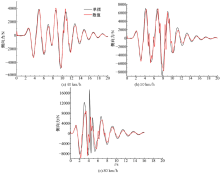
(1)50 km/h的时域响应对比:图12是50 km/h的不同模型计算结果对比, 该车速的车辆响应能够反映响应较稳定的各车速下不同模型的典型区别。

准静态结果与刚体结果相比:准静态模型计算的横摆角速度、侧向加速度、侧倾角和LTR值比刚体模型计算结果相差一个稳定的量, 而质心侧偏角除峰值的一些差异, 基本一致。这说明在该工况下, 液面倾角导致的横向载荷转移对车辆响应有一定的影响, 准静态的LTR稳定值比刚体模型大12.23%。

单摆结果与数值结果相比:二者计算的车辆响应和液体晃动侧向力基本一致, 说明此时液体的高阶晃动和非线性特性未被激发。

单摆结果与准静态结果相比:单摆模型的各项响应指标都具有长时间波动, 大多稳态响应与准静态一致, 但单摆计算的稳态侧倾角更大, 且单摆的侧偏角响应大幅放大, 响应幅值是准静态值的2~3倍, 并且伴有长时间波动。说明即使在开环稳定工况, 液体晃动对车辆各响应影响都很大, 不能忽略。

	Figure Option View Download New Window
	图12 阶跃工况50 km/h的仿真结果Fig.12 Results of step manoeuver at 50 km/h

(2)随着车速增大, 单摆模型和数值模型之间的差别增大, 体现在计算的横向晃动力/晃动力矩的差别增大, 以及车辆响应差别增大。

图13(a)为70 km/h时液体的晃动力, 与图12(f)相比, 70 km/h时单摆模型的晃动幅值更大, 而数值模型的晃动更复杂, 波动频率更高。

图13(b)(c)为70 km/h的车辆响应, 可以看出单摆模型计算的侧倾角更大, LTR达到1的时间更长, 这与50 km/h情况不同。

	Figure Option View Download New Window
	图13 阶跃工况70 km/h的仿真结果Fig.13 Results of step manoeuver at 70 km/h

	Figure Option View Download New Window
	图14 正弦工况-方向盘转角Fig.14 Steering wheel angle sinusoidal input

3.2 正弦工况

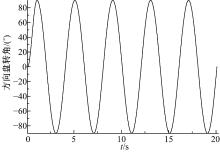
采用峰值A=90° , 周期T=4 s的方向盘转角正弦工况。图14为方向盘转角曲线。

仿真分析中, 单摆模型计算结果在100 km/h发生侧翻, 因此考虑40~99 km/h的情况。

通过对比不同车速、不同模型计算的结果, 并对比阶跃工况响应的特点, 具有如下发现:

(1)50 km/h的时域响应对比:

与阶跃工况不同, 不同模型的横摆角速度和侧向加速度差别不大, 以横摆角速度为例, 见图15(a)。

而对于侧偏角、侧倾角和LTR响应, 各模型计算结果的频率一致, 幅值不同, 以侧倾角为例, 见图15(b):刚体模型和准静态模型的响应结果幅值较小; 相比于刚体模型, 准静态模型的侧倾角响应更大; 单摆模型和数值模型计算的车辆响应结果基本一致。响应中未出现与激励不同频率的晃动, 说明在正弦工况中, 液体晃动频率与激励一致。

(2)随着车速增大, 单摆模型和数值模型之间的差别增大。与阶跃工况一致, 随着车速增大, 单摆模型的晃动幅值更大, 而数值模型的晃动更复杂; 单摆模型的侧倾角和LTR峰值更大。

	Figure Option View Download New Window
	图15 正弦工况50 km/h仿真结果Fig.15 Results of sine manoeuver at 50 km/h

3.3 双移线工况

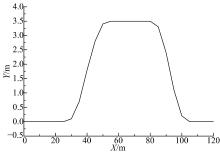
按照国标, 双移线目标轨迹设置如图16所示。

	Figure Option View Download New Window
	图16 双移线轨迹设置Fig.16 Track geometry of double lane change(DLC)maneuver

	Figure Option View Download New Window
	图17 双移线工况50 km/h方向盘转角Fig.17 Steering wheel angle in DLC at 50 km/h

	Figure Option View Download New Window
	图18 双移线工况-液体横向晃动力对比Fig.18 Liquid slosh force in DLC manoeuver

仿真分析中, 单摆模型计算结果在85 km/h发生侧翻, 因此考虑了40~84 km/h的情况。通过对比不同车速、不同模型计算的结果, 发现如下:

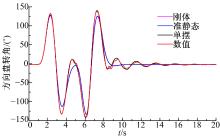
(1)50 km/h的时域响应为例:

图17为采用不同液体模型时, 驾驶员预瞄得到的方向盘转角曲线, 可以看出:刚体模型与准静态模型的方向盘转角接近, 单摆模型和数值模型的接近, 单摆和数值模型的方向盘转角比准静态模型有更多波动。

不同模型计算的车辆响应间的区别与阶跃工况类似。

(2)随着车速增大, 如图18所示, 对比40、50和80 km/h的液体晃动力:可以看出, 40 km/h时, 单摆和数值模型的晃动力吻合很好, 50 km/h时, 幅值差不多, 但数值模型的晃动更复杂, 成分更多, 80 km/h时, 数值模型存在更高阶的晃动但单摆模型的幅值比数值模型高。

3.4 液体响应成分对车辆响应峰值的影响

图19(a)~19(f)为不同工况时, 不同车速、不同模型计算的侧倾角峰值和LTR峰值。

	Figure Option View Download New Window
	图19 各种工况下不同模型的峰值响应对比Fig.19 Peak value responses in different manoeuvers

由图可以看出, 三种工况中, 不论是侧倾角峰值还是横向载荷转移率峰值, 刚体模型计算结果小, 准静态次之; 车速较低时, 单摆模型结果与数值结果吻合较好, 但随着车速增大, 单摆模型的侧倾角比数值结果大, LTR也更大, 且在接近侧翻的10 km/h车速内误差较明显, 虽然车速达到临界车速时, 二者LTR回归相等(上限是1), 但其实在动态时历曲线中, 单摆计算的LTR更多的时间达到1。说明:液面倾角和一阶晃动增大了侧倾和LTR响应, 而一阶晃动(单摆)在中低车速时基本能表征液体晃动特性, 接近侧翻时, 高阶晃动被激发, 缓和了一阶晃动对稳定性的负面影响, 经观察, 侧向加速度达到0.5 g(g=9.8 m²/s)时, 高阶晃动的缓和效应变得明显。

此外, 对于不同工况, 四种模型计算结果的差别也不同:正弦工况和阶跃工况中, 单摆模型对LTR幅值的估计较接近数值模型, 而双移线工况中, 中等车速时单摆模型估计值相对于数值结果的误差比前两个工况大。

这说明:复杂、闭环工况中, 液体高阶晃动和非线性特性更容易被激发, 因此在控制当中, 尤其是在稳定性等极限工况控制中, 用单摆模型模拟液体晃动准确性不够, 需要进一步修正。

3.5 液体响应成分对操纵稳定极限的影响

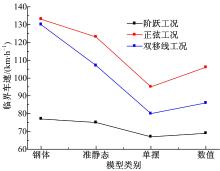
图20为三种工况下, 不同模型计算的侧翻临界车速。

	Figure Option View Download New Window
	图20 各工况下的临界车速Fig.20 Critical speed under different manoeuvers

可以看出, 不论采用哪种模型模拟液体货物部分, 本文采用的三种工况的临界车速具有大小关系:正弦工况> 双移线工况> 阶跃工况;

对于每种工况, 基于不同液体模型计算的临界车速具有如下大小关系:刚体> 准静态> 数值> 单摆模型。鉴于基于数值模型的液罐车动力学模型基本可反映真实液罐车的情况, 因此可以认为一般情况下, 单摆模型会低估液罐车的侧翻稳定性, 准静态模型会高估, 而刚体模型比数值模型的临界值高太多, 基本不能反映车辆真实的侧翻稳定性。

以数值模型计算的不侧翻临界车速为基准, 计算各工况下不同模型临界车速的误差, 如表2所示。

表2 不同模型临界车速的误差 Table 2 Error of critical speed of different model %

对于开环较稳定的阶跃工况, 刚体模型、准静态模型和单摆模型与数值结果之间的差别都相对其他工况较小。这说明该工况下, 液面倾角、一阶和高阶液体晃动对整车响应影响相对较小。

单摆模型误差均为负值, 这说明:高阶晃动有利于车辆的稳定性, 能减少一阶晃动带来的影响。同时, 单摆模型误差的数值相比于刚体模型和准静态模型的误差更小, 说明:只考虑一阶晃动虽然低估液罐车的稳定性, 但更接近实际情况。

刚体模型在复杂的闭环工况中, 偏差高达50%, 基本不能反映车辆真实的侧翻稳定性情况。

4 结束语

本文建立了液罐车辆在操纵工况下的四种动力学模型:基于等质量刚体的模型, 基于准静态液体的模型, 基于一阶等效单摆的模型和基于液体晃动数值模型的液罐车动力学模型。通过对比不同车速的阶跃工况、正弦工况和双移线工况下各模型计算的车辆响应, 分析了不同工况及剧烈程度下各液体响应成分的被激发程度及其对整车响应的影响大小。主要对以下三个方面进行了分析:①对不同工况, 对比了不同模型计算的车辆响应时间历程; ②对不同工况, 对比了不同模型计算的车辆响应峰值; ③对不同工况, 对比了不同模型计算的侧翻临界车速。得出了以下主要结论:

(1)液面倾角对车辆响应的稳态值和峰值会造成一定影响; 液体晃动则导致或放大车辆响应的振动。

(2)各模型对车辆操纵稳定性的估计具有如下大小关系:刚体≥ 准静态> 数值> 单摆模型。刚体基本不能描述液罐车的操纵响应及其稳定性极限, 准静态会高估液罐车的操纵稳定性, 而单摆模型会低估, 单摆模型是比刚体和准静态更接近液罐车的实际情况(即数值模拟的情况)。

(3)单摆模型代表的一阶晃动在中、低车速时能很好的温和实际情况, 但接近极限时高阶和非线性晃动开始占据晃动主导地位, 单摆模型准确性变差。

(4)相比于双移线工况, 阶跃工况和正弦工况中单摆模型对车辆响应幅值的估计更接近数值情况, 说明复杂、闭环工况中, 液体高阶晃动和非线性特性更容易被激发。

根据以上对液罐车动力学响应特性的分析结论, 本文也给出一些建立液罐车内液体晃动简化模型的建议:

由于复杂、闭环工况, 以及临近失稳工况时, 高阶晃动和液体非线性特性占据晃动主导地位, 并对稳定性极限有重要影响, 因此建立用于液罐车辆系统分析的液罐车动力学封闭方程时, 必须考虑高阶非线性晃动特征, 该特征会削弱低阶晃动的不良影响。

用于液罐车辆稳定性控制的简化模型, 对模型准确性和计算速度都有一定要求, 考虑到中低车速时单摆模型对液体晃动的模拟准确性较高, 而在接近侧翻的10 km/h车速内, 或侧向加速度达到0.5 g时, 准确性迅速降低, 因此可以在临近侧翻的一定范围内考虑高阶晃动, 而在中低车速、较稳定工况中仅用一阶单摆模拟液体晃动。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	李显生, 郑雪莲, 刘宏飞. 非满载罐式半挂汽车列车侧倾稳定性评价改进算法[J]. 吉林大学学报: 工学版, 2012, 42(5): 1089-1094. Li Xian-sheng, Zheng Xue-lian, Liu Hong-fei. Improved algorithm on roll stability evaluation of partially filled tractor-tank semitrailer[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(5): 1089-1094. [本文引用:1]
[2]	郑雪莲, 李显生, 任园园, 等. 非满载汽车罐车液体冲击等效机械模型[J]. 吉林大学学报: 工学版, 2013, 43(6): 1488-1493. Zheng Xue-lian, Li Xian-sheng, Ren Yuan-yuan, et al. Equivalent mechanical model for liquid sloshing in partially-filled tank vehicle[J]. Journal of Jilin University(Engineering and Technology Edition) , 2013, 43(6): 1488-1493. [本文引用:1]
[3]	岳宝增, 祝乐梅, 于丹. 储液罐动力学与控制研究进展[J]. 力学进展, 2011, 41(1): 79-92. Yue Bao-zeng, Zhu Le-mei, Yu Dan. Recent advances in liquid-filled tank dynamics and control[J]. Advances in Mechanics, 2011, 41(1): 79-92. [本文引用:1]
[4]	Kolaei A, Rakheja S, Richard M J. Effects of tank cross-section on dynamic fluid slosh loads and roll stability of a partly-filled tank truck[J]. European Journal of Mechanics B-Fluids, 2014, 46: 46-58. [本文引用:1]
[5]	Bottiglione F, Mantriotta G. Field tests and validation of dynamical models of tank vehicles Part II: experimental tests and results[J]. International Journal of Heavy Vehicle Systems, 2012, 19(1): 23-39. [本文引用:1]
[6]	陈铭年. 油罐车转弯横向稳定性的计算分析[J]. 汽车工程, 2001, 23(5): 359-360. Chen Ming-nian. Calculate analysis of transversal stabilization for turning of oil tank truck[J]. Automotive Engineering, 2001, 23(5): 359-360. [本文引用:1]
[7]	胡晓明, 李万莉, 赵志国, 等. 液罐车罐体内液体横向晃动研究[J]. 应用力学学报, 2013, 30(5): 641-646. Hu Xiao-ming, Li Wan-li, Zhao Zhi-guo, et al. Horizontal fluid sloshing analysis in the body of tank truck[J]. Chinese Journal of Applied Mechanics, 2013, 30(5): 641-646. [本文引用:1]
[8]	Mantriota G. Directional stability of articulated tank vehicles: A simplified model[J]. International Journal of Heavy Vehicle Systems, 2003, 10(1): 144-165. [本文引用:1]
[9]	Acarman T, Ozguner U. Rollover prevention for heavy trucks using frequency shaped sliding mode control[J]. Vehicle System Dynamics, 2006, 44(10): 737-62. [本文引用:1]
[10]	郑雪莲, 李显生, 任园园, 等. 瞬时液体冲击对汽车罐车侧倾稳定性的影响[J]. 吉林大学学报: 工学版, 2014, 44(3): 625-630. Zheng Xue-lian, Li Xian-sheng, Ren Yuan-yuan, et al. Rollover stability analysis of tank vehicle impacted by transient liquid sloshing[J]. Journal of Jilin University(Engineering and Technology Edition) , 2014, 44(3): 625-630. [本文引用:1]
[11]	Modaressi-Tehrani K, Rakheja S, Stiharu I. Three-dimensional analysis of transient slosh within a partly-filled tank equipped with baffles[J]. Vehicle System Dynamics, 2007, 45(6): 525-548. [本文引用:1]
[12]	Hakan A. A numerical study of the effects of the vertical baffle on liquid sloshing in two-dimensional rectangular tank[J]. Journal of Sound and Vibration, 2012, 331: 41-52. [本文引用:1]
[13]	Wasfy T M, O'Kins J, Smith S. Expermental validation of a coupled fluid-multibody dynamics model for tanker trucks[C]∥SAE Paper2008-01-0777. [本文引用:1]
[14]	Cheli F, D'Alessand ro V, Premoli A, et al. Simulation of sloshing in tank trucks[J]. International Journal of Heavy Vehicle Systems, 2013, 1744232X. [本文引用:1]
[15]	Azadi S, Jafari A, Samadian M. Effect of parameters on roll dynamic response of an articulated vehicle carrying liquids[J]. Journal of Mechanical Science and Technology, 2014, 28(3): 837-848. [本文引用:1]
[16]	Fleissner F, Lehnart A, Eberhard P. Dynamic simulation of sloshing fluid and granular cargo in transport vehicles[J]. Vehicle System Dynamics, 2010, 48(1): 3-15. [本文引用:1]

2012

0.0

. 2012, 42(5):1089-1094

Improved algorithm on roll stability evaluation of partially filled tractor-tank semitrailer

非满载罐式半挂汽车列车侧倾稳定性评价改进算法

Li Xian-sheng , Zheng Xue-lian , Liu Hong-fei.

李显生, 郑雪莲, 刘宏飞

From the fact that the quasi-static method has deficiency in the solution of the transient mass center of sloshing fluid and the corresponding vehicle rollover modelling, the solutions of the transient mass center of sloshing fluid in tanks with modified square and modified oval cross sections were improved, and the exact equations for the mass center in the tank with modified square cross section were derived. A new vehicle rollover model was built without uncommon and hard-to-get parameters, simplifying the solution of vehicle rollover threshold. Using the improved quasi-static method, the change of the vehicle rollover threshold with filling percent under conditions of constant cargo density and constant cargo mass was simulated by Matlab. The results showed that the improved quasi-static method can predict accurately the vehicle rollover threshold.

针对传统准静态(QS)方法在瞬时液体质心的求解和车辆侧倾模型两方面存在的缺陷和不足,改进了改良的方形和椭圆形横截面罐体内瞬时液体质心的求解过程,并推导了改良方形罐体内液体质心的求解公式。重新建立了车辆侧倾模型,避免了不常见和难获得车辆参数的使用,简化了侧倾极限值的求解。利用改进的QS方法通过Matlab对液体密度固定和载质量固定两种情况下的车辆侧倾极限值随充液比的变化进行了仿真。仿真结果表明:改进的QS方法可准确地预测车辆侧倾极限值。

... 目前的液体简化模型主要有准静态模型^[1]和机械力学等效模型^[2](以单摆模型和弹簧-质子模型为主),准静态模型无法反映液体的动态变化和晃动,单摆、弹簧-质子等目前的等效力学模型只能反映液体在线性或弱非线性范围内的晃动情况^[3],对于临近危险工况时可能被激发的非线性特性无法描述,且现在的液罐车必须安装隔板,大多隔板带有空洞,对这种罐体的纵向晃动和纵向液体流动,目前的机械力学模型还不能描述 ...

2013

0.0

. 2013, 43(6):1488-1493 DOI:doi:10.7964/jdxbgxb201306009

Equivalent mechanical model for liquid sloshing in partially-filled tank vehicle

非满载汽车罐车液体冲击等效机械模型

Zheng Xue-lian , Li Xian-sheng , Ren Yuan-yuan

郑雪莲, 李显生, 任园园

A trammel pendulum model to simulate liquid sloshing in tanks with circular and oval cross-sections is developed. Motion equations of the trammel pendulum in inertial coordinate system, non-inertial coordinate system, and in a coordinate system that moves in a complex way are derived. In the inertial coordinate system, the motion equation of trammel pendulum is numerically solved. The angular position, angular velocity and hunting frequency of the pendulum are analyzed. It is found that a linear trammel pendulum model can be used to simulate liquid sloshing in partially-filled tank vehicles. This research can provide theoretical basis and actual assistance to investigate the performance, driving stability and auxiliary driving technology of tank vehicles.

针对圆柱和椭圆柱罐体内的液体冲击运动,构建了椭圆规钟摆模型,用来模拟罐体内的液体冲击运动。推导了惯性坐标系、非惯性坐标系和复杂运动坐标系下的钟摆运动方程,并对惯性坐标系下的钟摆运动方程进行了数值求解。分析了钟摆摆角、角速度、振荡频率的变化规律,获得了可用线性椭圆规钟摆近似模拟罐车罐体内液体冲击的结论。研究结果可以为汽车罐车性能分析、行驶稳定性技术和辅助驾驶技术的研发提供理论依据和实际支持。

2011

0.0

. 2011, 41(1):79-92 DOI:doi:10.6052/1000-0992-2011-1-lxjzj2010-054

Recent advances in liquid-filled tank dynamics and control

储液罐动力学与控制研究进展

Yue Bao-zeng , Zhu Le-mei , Yu Dan.

岳宝增, 祝乐梅, 于丹

The engineering application background of liquid-filled tank dynamics and control is presented. Recent advances in liquid-filled tank dynamics and control are systematically reviewed in terms of the following three aspects, i.e. liquid sloshing dynamics, liquid sloshing equivalent mechanical model and multi-body dynamics and control for liquid-filled tanks. Liquid sloshing dynamics in tanks are overviewed from analytical methods to numerical methods. In the part of multi-body system dynamics and control, the research progresses for vehicle and ship tank system dynamics and liquid-filled spacecraft dynamics and control are provided. Finally, key topics for further research are pointed out.

阐述了储液罐动力学与控制的工程应用背景, 从3个方面回顾了储液罐动力学与控制的研究进展, 即: 储液罐类液体晃动动力学、液体晃动等效力学模型和储液罐多体系统动力学与控制. 其中对储液罐类液体晃动动力学的研究成果从解析方法和数值方法两方面进行了概述; 在储液罐多体系统动力学中概述了车载、船载储液罐系统动力学和充液航天器固--液--控耦合动力学近年来的研究成果.对今后需要进一步开展的研究方向进行了展望.

2014

0.0

2012

0.0

2001

0.0

. 2001, 23(5):359-360 DOI:doi:10.3321/j.issn:1000-680X.2001.05.017

Calculate analysis of transversal stabilization for turning of oil tank truck

油罐车转弯横向稳定性的计算分析

Chen Ming-nian.

陈铭年

油罐车平地急转弯和坡上转弯是容易引起横向翻倾的危险工况.由于油罐留有扩大容量和油液的流动性,转弯时油液质心偏移,导致横向稳定性减弱.本文分析并推导了具有椭圆截面罐体的油罐车转弯时的横向翻倾临界坡度角和转向加速度的计算公式,介绍了横向稳定特性曲线的绘制方法,并给出了计算实例.

... 分析液罐车响应特性方面的研究不少,但大多局限于以下两个方面:①结合简化液体模型(主要为准静态^[6]或单摆模型^[7,8,9],或在准静态基础上引入瞬态峰值系数^[10])和车辆模型(车辆模型或为临界方程,或为动态方程),分析侧翻临界车速、整车响应特性、液体倾角和液体晃动等对整车响应的影响,但由于目前的简化液体模型不能充分反映液体的动力学特性,因此获得的分析结果的准确性和指导意义有限 ...

2013

0.0

. 2013, 30(5):641-646 DOI:doi:10.11776/cjam.30.05.A038

Horizontal fluid sloshing analysis in the body of tank truck

液罐车罐体内液体横向晃动研究

Hu Xiao-ming , Li Wan-li , Zhao Zhi-guo

胡晓明, 李万莉, 赵志国

为研究液体晃动对液罐车行驶稳定性的影响,针对罐体内液体的横向晃动问题,运用势流理论建立了液体晃动的控制方程,并采用Galerkin方法进行了求解;根据等效原则建立了罐体内液体晃动的弹簧-质量-阻尼等效力学模型,通过与试验数据的比较,验证了文中的求解过程及建立等效模型方法的正确性。运用建立的等效模型,通过具体算例分析了液体晃动特征频率和等效模型参数随充液比的变化关系、车辆的侧向加速度和充液比对罐体的横向作用力和力矩的影响。结果表明:在液体晃动中,第一阶晃动质量起主导作用,在精度要求不高的情况下,可以考虑只建立一阶等效系统;液体晃动第一阶特征频率随充液比的增加而增加,第二、第三阶特征频率随充液比的增加先减小再增加;罐车转向运动时,充液比在λ为0.8-1.0时液体晃动最剧烈,并且液体对罐体的作用力和力矩均随侧向加速度的增加而增加。

2003

0.0

2006

0.0

2014

0.0

. 2014, 44(3):625-630 DOI:doi:10.13229/j.cnki.jdxbgxb201403007

Rollover stability analysis of tank vehicle impacted by transient liquid sloshing

瞬时液体冲击对汽车罐车侧倾稳定性的影响

Zheng Xue-lian , Li Xian-sheng , Ren Yuan-yuan

郑雪莲, 李显生, 任园园

为了探究准静态(Quasi-static,QS)方法对液体冲击的估计精度以及对汽车罐车准静态侧倾稳定性分析的准确性,分析了非满载椭圆柱罐体内瞬时液体冲击的实际值与QS方法估计值之间的关系。在此基础上,通过分析液体质心位移引起的车辆侧翻力矩和轮胎垂直载荷转移引起的回正力矩之间的平衡,研究了瞬时液体冲击对车辆侧倾稳定性的影响。并根据不同罐体车辆侧倾稳定性的分析结果,研究了影响液体冲击强度的关键因素和最优罐体形状。

2007

0.0

... ②基于流体CFD软件建立罐内液体数值模型,分析简单激励下液体晃动力和晃动力矩及其受充液比、罐体形状等的影响^[11,12],没有考虑实际工况和车辆动力学带来的复杂激励,且无法给出液体特性对车辆响应的影响 ...

2012

0.0

2008

0.0

... 极少数研究结合数值液体模型和车辆模型分析液罐车辆的响应^[13,14] ...

2013

0.0

... 极少数研究结合数值液体模型和车辆模型分析液罐车辆的响应^[13,14] ...

2014

0.0

2010

0.0