本文以某205/55R16轿车子午线轮胎为研究对象, 利用文献[5]的方法建立其有限元模型。首先, 提取轮胎断面并进行扫描, 利用CAD软件建立轮胎的二维断面几何模型; 将几何模型导入Hypermesh软件, 并对其进行网格划分。使用Abaqus/Standard中的rotate命令将轮胎二维截面旋转为三维网格模型, 如图1所示。模型中采用YEOH本构模型拟合橡胶材料的应力应变关系^[6], 采用Rebar单元模拟橡胶-帘线复合材料。使用Abaqus中的CGAX3H和CGAX4H单元模拟轮胎的受力特性; 使用DCAX3和DCAX4单元模拟橡胶的传热特性。转鼓采用解析单元模拟, 轮胎与轮辋为过盈配合边界; 轮胎胎压设置为210 kPa, 载荷设为4475 N。为准确模拟轮胎温度场, 利用Fluent软件将轮胎、转鼓以及周围的空气域作为一个整体来计算轮胎的对流换热系数。考虑计算过程中的计算效率与计算精度, 轮胎与转鼓外部空气域尺寸通过试算获得:长为3R₁+3R₂, 宽为5H, 高为3R₂。其中, R₁为轮胎直径, R₂为转鼓直径, H为转鼓宽度。轮胎旋转方向的四个平面为封闭面, 另两面为开放面, 气压设定为标准大气压, 室温及转鼓温度设置为25 ° C。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 轮胎三维有限元模型Fig.1 Three-dimensional FEA of radial tire

1.2.1 计及环境影响的轮胎温度场模型

橡胶材料的力学特性与温度关系密切^[7]。但在以往的研究中, 轮胎温度场模拟只考虑轮胎本身的温度变化, 忽视了环境对于轮胎温度的影响^[8]。为了获得更准确的轮胎温度场模型, 本文在考虑轮胎内部换热的同时, 也考虑轮胎外部环境对轮胎温度的影响。使用Hypermesh中的CFD tetra mesh命令进行轮胎外部流场的CFD网格划分, 划分完成的轮胎外部环境CFD流体网格截面图如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 轮胎外部环境CFD流体网格截面图Fig.2 Cross section of CFD mesh

外部环境对于轮胎温度场的影响能够反映为轮胎表面的热辐射以及热对流边界条件, 其中橡胶材料的热辐射系数设为定值0.95^[9], 轮胎表面的对流换热系数通过Fluent软件中的CFX模块进行计算, 计算结果如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 轮胎外部环境流场分布Fig.3 Fluid field of radial tire

为了便于研究, 轮胎温度场简化为二维模型, 因此需要将三维模型的对流换热系数映射到二维模型上。

Q=hAΔt（1）

式中:A为固体表面与流体的接触面积; Q为面积A上的传热热量; h为表面对流换热系数; Δ t为固体表面与流体的温度差。

由于轮胎表面点离旋转轴的距离越远, 其对流换热系数越大^[10], 因此, 将轮胎外表面按距旋转轴的距离划分为14段表面, 采用基于三角形的一阶线性插值拟合曲面, 并求出均值, 得到轮胎单位面积的对流换热系数。

为分析轮胎温度场, 本文使用Hot Disk热常数分析仪分析了轮胎所用胶料的热物性参数。轮胎内部温度场利用文献[11]的方法, 使用Abaqus软件模拟轮胎内部传热, 建立计及轮胎内部空气域的温度场模型。使用Abaqus热传导分析中的* SRADIATE命令以及* SFLIM命令定义轮胎表面的热辐射系数以及对流换热系数。

1.2.2 温度耦合的轮胎滚动阻力计算方法

轮胎的滚动阻力主要由轮胎与路面间的摩擦损失以及橡胶材料的迟滞损失组成, 其中迟滞损失占滚动阻力的90%~95%^[5], 当只考虑轮胎的迟滞损失时, 轮胎旋转一周的滚动能量损失以及滚动阻力的计算公式如下:

ELOSS=∑QiVi（2）

FR=ELOSSC（3）

Qi=∑n=1mnπσn¯¯εn¯¯sinδ（4）

tanδ=G″/G'（5）

式中:E_LOSS为轮胎旋转一周的总能量损失; Q_i为橡胶材料单位体积迟滞能量损失; V_i为轮胎橡胶单元体积; F_R为轮胎的滚动阻力; C为轮胎周长; m为橡胶单元的数量; σn¯¯为等效应力; εn¯¯为等效应变; tanδ 为橡胶材料的损耗因子; G″为橡胶材料的储能模量; G'为橡胶材料的损耗模量。

本文使用DMA测试仪测量橡胶材料的损耗因子、温度以及应变三者之间的关系, 通过轮胎有限元力学模型以及温度场模型得到轮胎不同位置处的应变数据以及温度数据, 即可求得轮胎不同位置处的损耗因子。使用Matlab软件和文献[11, 12]的方法编写耦合温度影响的轮胎滚动阻力计算程序。

1.3.1 轮胎温度测试

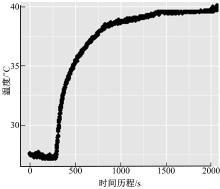
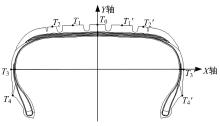
使用在线式红外测温仪测量轮胎胎冠最高点处的温度变化, 如图4所示。由图4可知, 经过35 min轮胎表面温度趋于稳定, 此时轮胎温度达到稳态。在此基础上, 为验证轮胎温度仿真模型的可靠性, 待轮胎温度稳定后, 使用热电偶测温仪对轮胎外表面点进行测量。测试时, 选取胎面处5个点、胎侧最宽点以及胎圈上部点为测量点, 测量点分布位置如图5所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 轮胎表面升温历程Fig.4 Elevated temperature curve of tire surface

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 轮胎测温试验测点分布Fig.5 Test points arrangement of tire surface

表1为轮胎温度场的仿真值与试验值结果对比。由表1可知, 轮胎温度场仿真结果与试验结果有着良好的一致性:轮胎胎侧以及轮辋处试验值与仿真值最大误差为3.34%, 轮胎胎肩处以及胎面处试验值与仿真值最大误差为9.52%。存在误差的主要原因是在试验过程中难以控制热电偶测温仪与轮胎之间的接触压力, 测温过程中轮胎会有一定的热量流失, 另外, 仿真时未考虑轮胎与转鼓之间的接触传热。但仿真值与试验值的一致性较好, 误差均为10%以内, 这说明本文使用的温度场建模方法用于轮胎温度场仿真是合理可信的。

1.3.2 轮胎滚动阻力测试

参照ISO28580标准, 使用图6所示的轮胎

表1

Table 1

表1(Table 1)

表1 轮胎测温试验值与仿真结果对比 Table 1 Comparison of temperature between experiment and simulation results 项目 轮胎表面点编号 T4 T3 T2 T1 T0 T'1 T'2 T'3 T'4 试验温度/° C 39.5 38 43.6 39.4 40 39.6 43.6 37 37.8 仿真温度/° C 38.18 38.25 47.75 41.5 41.3 40.8 43.81 37.94 37.17 误差/% 3.34 -0.66 -9.52 -5.33 -3.25 -3.03 -0.48 -2.54 1.67

表1 轮胎测温试验值与仿真结果对比 Table 1 Comparison of temperature between experiment and simulation results

滚动阻力测试台对205/55R16轮胎进行滚动阻力测试。试验时, 轮胎速度为80 km/h, 胎压为210 kPa, 载荷为4475 N。实验室内恒温25 ° C。滚动阻力测试前, 被测轮胎需在25 ° C恒温下放置2.5 h, 以保证轮胎内部温度一致。轮胎滚动阻力试验与仿真结果对比如表2所示。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 轮胎滚动阻力测试台Fig.6 Test bench of rolling resistance

表2

Table 2

表2(Table 2)

表2 轮胎滚动阻力试验结果对比 Table 2 Comparison of rolling resistance between experiment and simulation results 项目 滚动阻力/N 滚动阻力系数 试验值 48.88 10.92 仿真值 50.12 11.2 误差/% 2.53 2.53

表2 轮胎滚动阻力试验结果对比 Table 2 Comparison of rolling resistance between experiment and simulation results

由表2可知, 计及温度影响的轮胎滚动阻力仿真结果与试验结果偏差较小, 误差均为2.53%。可见, 本文建立的滚动阻力计算方法是准确可信的。

轮胎轮廓形状直接影响其帘线以及橡胶材料的受力状态, 从而影响到轮胎的滚动阻力、寿命等一系列基本性能^[1]。以往的轮胎轮廓设计过程中, 由于没有充分考虑橡胶材料的受力特性, 橡胶材料的应力分布十分不均匀:多数橡胶材料处于低应力状态, 利用率较小; 少数橡胶材料处于高应力状态, 容易产生破坏。同时现有的轮胎轮廓设计方法中, 没有直接针对轮胎外轮廓的设计方法。

满应力设计方法的思想是在不影响结构寿命的前提下, 使结构构件中最小应力接近或达到材料的许用应力, 同时降低结构中的最大应力, 从而使得结构材料得到充分的运用^[13]。其优化思路被广泛运用在桥梁、水坝、建筑等领域。因此, 在不影响轮胎寿命的前提下, 应用满应力设计方法进行轮胎外轮廓设计, 降低轮胎质量, 同时实现轮胎滚动阻力的优化是可行的。

荣见华等^[14]提出了渐进结构优化方法(Evolutionary structural optimization, ESO)。ESO的基本思想为:基于一定的删除准则, 通过数值分析结果, 逐步将无用或者低效单元删除, 以达到结构的最优化。该方法具有良好的通用性与工程实用性, 优化结果能够直接运用于工程实际。

研究表明^[15], 轮胎滚动阻力与其质量密切相关。根据轮胎生产企业的要求, 本研究以轮胎疲劳寿命为约束条件, 应用满应力理论, 找到轮胎外轮廓设计区域中应力较小的部分。在此基础上, 利用渐进结构优化方法, 以轮胎质量为结构优化参数, 对轮胎轮廓进行优化设计。轮胎外轮廓优化方程可写成如下形式:

X=x1, x2, …, xi（6）

minW=∑i=1NWiβi（7）

式中:X为优化设计区间, 本文选取轮胎外轮廓向内3 mm为优化设计区间; x_i为优化区间内的橡胶单元; W为橡胶单元的质量; 设计变量β _i为离散值, 取0或1, 当删除单元时取0, 当保留单元时取1; N为优化单元总数。

本文采用无量纲参数应变能密度梯度(Strain energy density gradient, SEDG)来评价轮胎的使用寿命, 该方法已在研究水坝强度、地震预测方面得到广泛应用^[16], 在轮胎疲劳中也得到应用。本文以轮胎易破坏区域的SEDG以及轮胎易破坏点处的应变能密度(Strain energy density, SED)作为约束条件:

SEDGK≤SEDGK-1（8）

SEDK≤SEDK-1（9）

式中:K为迭代步编号; SEDG_K、SEDG_K-1分别为第K、K-1步胎肩处SEDG最大值; SED_K、SED_K-1分别为第K、K-1步轮胎二号带束层端部处的SED。

对于每一个设计区域内的橡胶单元, 判断是否满足:

σiK/σMAXK≤RRK（10）

如满足, 则认为单元i在整个机构中处于低应力状态, 对于机构整体的贡献度较小, 可从机构中删除。如不满足, 则不对其进行修改。其中, σiK为第K步轮胎接地区域每一个橡胶单元的Von Mises应力, σMAXK为第K步结构的最大Von Mises应力; RR_K为第K次迭代时的单元删除率:

RRK+1=RRK+ER（11）

式中:RR_K+1为第K+1次迭代时的单元删除率; ER为迭代进化率, 其取值大小根据试算决定。本文中初始单元删除率RR₀与ER分别取1%和0.5%。

为了降低迭代过程中出现奇异解的可能性, 同时减少优化迭代次数, 当第K次迭代不满足约束条件时, 丢弃第K次迭代的计算结果, 基于第K-1次迭代结果重新进行优化计算, 此时的单元删除率为:

RRK+1=RRK/2（12）

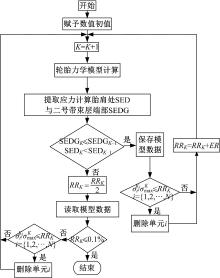
当RR_K+1≤ 0.1%时, 或优化删除的橡胶单元超出设计区间, 则认为计算收敛, 此时结束优化计算。为了保证轮胎外轮廓的平滑性, 基于优化完成的网格结构, 使用样条曲线进行轮胎轮廓的重建。本文提出的应用满应力理论的轮胎轮廓设计方法流程图如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 应用满应力理论的轮胎轮廓优化流程图Fig.7 Flow chart of optimization based on full stress design

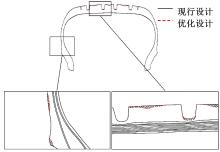
经过13次迭代, 模型计算收敛, 轮胎现行设计与优化设计轮廓对比如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 现行设计与优化设计轮廓对比Fig.8 Comparison between current and modified contour of radial tire

由图8可知, 与现行轮廓设计相比, 应用满应力设计的轮胎外轮廓曲线修改了胎面胶以及胎侧胶两处胶料的结构:胎面呈现两段弧分布; 胎冠最高点略微下降; 纵沟深度有所增加; 轮胎最宽点处以及胎侧与胎圈交界处的胶料有所减少。

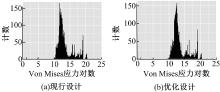
现行设计与优化设计接地断面处橡胶单元Von Mises应力分布对比如图9所示。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 轮胎接地处橡胶单元现行与优化设计受力对比Fig.9 Comparison of Von Mises between current and modified designs

由图9可知, 与现行设计相比, 应用满应力设计的轮胎橡胶单元受到的Von Mises应力均有所上升。优化设计减少了低应力单元数量, 同时也减少了高应力单元的Von Mises应力:接地面处的最小Von Mises应力由现行设计的106 Pa上升为优化设计的1.66× 10⁴ Pa; 接地面处的最大Von Mises应力由现行设计的4.98× 10⁹ Pa下降为优化设计的4.87× 10⁹ Pa。因此, 应用满应力理论设计的轮胎轮廓能够优化轮胎整体受力。

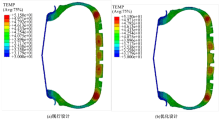
轮胎轮廓改进设计后轮胎整体温度场分布有所改变, 如图10所示。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 现行设计与优化设计轮胎温度场计算结果对比Fig.10 Comparison of temperature field between current and modified designs

与现行设计相比, 应用满应力设计的轮胎胎面整体温度显著下降, 轮胎胎面以及胎肩处的高温区域缩小明显, 胎肩处的最高温度由51.5 ° C下降至49 ° C, 相对降低4.9%。由图10可知, 应用满应力理论设计的轮胎轮廓能够降低轮胎整体温度, 减少轮胎由于热量积蓄引起的爆胎现象。

温度耦合的轮胎各部件能量损失计算结果如表3所示。由表3可知, 满应力设计轮胎结构提升了胎面胶料的利用率, 因此胎面胶能量损失有所上升; 新的轮胎轮廓优化了轮胎整体的应力分布, 降低了整胎温度, 使得其他部件的能量损失均有所降低。

表3

Table 3

表3(Table 3)

表3 现行设计与优化设计轮胎各橡胶部件能量损失对比 Table 3 Comparison of energy loss between current and modified designs 轮胎部件 能量损失/J 现行设计 优化设计 内衬层 1.05 1.01 胎体层 6.22 5.56 带束层 8.29 7.84 冠带层 5.42 4.76 三角胶 5.01 4.35 耐磨胶 4.58 3.95 胎侧胶 1.58 1.54 胎面胶 41.76 41.92

表3 现行设计与优化设计轮胎各橡胶部件能量损失对比 Table 3 Comparison of energy loss between current and modified designs

现行设计与优化设计的滚动阻力及滚阻系数对比如表4所示。由表4可知, 应用满应力设计的轮胎滚动阻力有明显下降, 较现行设计降低了4%。因此, 应用满应力设计的轮胎轮廓能够调节轮胎的滚动阻力性能。

表4

Table 4

表4(Table 4)

表4 现行设计与优化设计滚动阻力对比 Table 4 Comparison of rolling resistance between current and modified designs 方案 滚动阻力/N 滚动阻力系数 现行设计 41.71 9.32 优化设计 40.04 8.95

表4 现行设计与优化设计滚动阻力对比 Table 4 Comparison of rolling resistance between current and modified designs

轮胎在使用过程中, 胎肩处由于应力集中、热量容易积蓄以及带束层端部与胶料之间相互磨损等因素, 极易产生破坏^[15]。大部分轮胎破坏由胎肩破坏引起, 因此轮胎胎肩处的寿命能够反映轮胎整体寿命的大小。

本文利用Matlab软件编写了针对轮胎胎肩处SEDG的计算程序, 现行设计与优化设计的轮胎胎肩处SEDG对比如图11所示。

图11

Fig.11

	Figure Option ViewDownloadNew Window
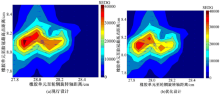	图11 现行设计与优化设计胎肩处SEDG值对比Fig.11 Comparison of the strain energy density gradient between current and modified designs

由图11可知, 与现行设计相比, 应用满应力设计的轮胎结构能够显著缓解胎肩处的应变能集中现象, 优化了胎肩处应力分布。如表5所示, 相较于现行设计, 应用满应力设计的轮胎降低了4.23%的胎肩处SEDG值, 同时降低了5.11%的二号带束层端部应变能。因此, 应用满应力理论设计轮廓的轮胎能够提升轮胎疲劳寿命。

表5

Table 5

表5(Table 5)

表5 现行方案与优化方案轮胎寿命评价指标对比 Table 5 Comparison of service life between current and modified designs 方案 二号带束层端部SED值 胎肩处最高SEDG值 现行设计 212209 41644 优化设计 201367 39882

表5 现行方案与优化方案轮胎寿命评价指标对比 Table 5 Comparison of service life between current and modified designs

轮胎轻量化设计不仅能够降低轮胎的滚动阻力, 同时能够减少橡胶材料的使用, 对于企业成本控制以及减少环境污染都有着重要意义。经过优化, 轮胎胎面胶以及胎侧胶所用胶料如表6所示。

表6

Table 6

表6(Table 6)

表6 现行设计与优化设计轮胎部件质量对比 Table 6 Comparison of mass between current and modified designs 方案 质量/kg 胎面胶 胎侧胶 现行设计 3.49 0.81 优化设计 3.32 0.77

表6 现行设计与优化设计轮胎部件质量对比 Table 6 Comparison of mass between current and modified designs

由表6可知, 与现行设计相比, 应用满应力设计的轮胎胎面胶以及胎侧胶使用量显著减少:胎面胶胶料减少了4.87%, 胎侧胶胶料减少了4.94%。轮胎橡胶使用量总体减少了210 g, 以205/55R16轮胎质量9.5 kg计算, 总质量减轻了2.2%。