丰田PRIUS混合动力汽车能量优化管理策略仿真分析

引用本文

夏超英, 杜智明. 丰田PRIUS混合动力汽车能量优化管理策略仿真分析. 2017, 47(2): 373-383
XIA Chao-ying, DU Zhi-ming. Simulation analysis on energy optimization strategy for Toyota PRIUD hybrid electric vehicle. Journal of Jilin University Engineering and Technology Edition, 2017, 47(2): 373-383 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201702005
Permissions

丰田PRIUS混合动力汽车能量优化管理策略仿真分析

夏超英, 杜智明

天津大学电气与自动化工程学院,天津 300072

作者简介:夏超英(1958-),男,教授,博士生导师.研究方向:节能与新能源汽车.E-mail:xiachaoying@126.com

基金项目:“863”国家高技术研究发展计划项目(2012AA111203).

摘要

针对丰田PRIUS混合动力汽车,提出一种基于二次型最优控制理论的新能量优化管理策略,该策略结合规则构造二次型性能指标,通过限制发动机功率的大幅频繁波动,在保证车辆动力性能的同时,达到间接降低整车油耗的控制目标。对ADVISOR软件进行了二次开发,建立了车辆仿真模型,并在不同工况下验证了策略的有效性。仿真结果表明:在不同的道路工况下,该能量优化管理策略比基于规则的能量管理策略具有更好的燃油经济性。

关键词: 车辆工程; 混合动力汽车; 能量管理策略; 二次型最优控制

中图分类号:U469 文献标志码:A 文章编号:1671-5497(2017)02-0373-11

Simulation analysis on energy optimization strategy for Toyota PRIUD hybrid electric vehicle

XIA Chao-ying, DU Zhi-ming

School of Electrical Engineering and Automation,Tianjin University,Tianjin 300072,China

Abstract

A new energy optimization strategy for Toyota PRIUS hybrid electric vehicle is proposed based on the linear optimal control theory. In this strategy a quadratic performance index is built combined with several rules to restrict frequent and large-scale fluctuation on engine output power, thus, realizing direct reduction of fuel consumption while still maintaining the vehicle good driving performance. Based on the second development of ADVISOR software, the vehicle simulation model is established to verify the effectiveness of the proposed strategy. Simulation results show that the energy optimization strategy has better oil-saving effect than the rule-based energy management strategy over different driving cycles.

Key words: vehicle engineering; hybrid electric vehicle(HEV); energy management strategy; quadratic optimal control

Show Figures

0 引言

混合动力汽车作为最具产业化前景的新能源汽车, 兼具传统内燃机汽车和纯电动汽车的优势, 能够有效缓解汽车产业发展带来的能源和环境压力。PRIUS(普锐斯)是丰田汽车公司最早商业化生产的混合动力汽车, 它采用行星排式混联拓扑结构, 成功实现了发动机和车轮之间转速和转矩的双解耦^[1]。PRIUS在量产车中采用基于规则的控制策略解决车辆能量协调控制的问题, 根据节气门开度和电池荷电状态(State of charge, SOC)将系统运行模式分为3种, 即发动机独立工作模式、电动机独立工作模式和混合工作模式, 通过动力分配机构调节和控制能量流动途径, 使发动机和电机在高效率区内工作^[2]。该策略实现简单, 但其模式切换规则的设计和控制参数的设置主要依靠设计人员的经验, 无法从理论上保证燃油经济性达到最优。

近年来, 各国研究者针对PRIUS的混联拓扑结构提出多种新的能量管理策略, 如Kim等^[3]提出的策略是利用发动机实际转速和目标转速之差对发电机转速进行PI控制, 而电动机则根据整车需求提供转矩补偿。Chen等^[4]提出基于模糊逻辑的在线自适应控制策略, 该策略首先通过动态规划(Dynamic programming, DP)算法得到指定工况下的最优解, 然后根据发动机与车辆需求功率的比值和电池SOC等变量建立隶属度函数及模糊规则, 结果表明, 即使对于选定工况, 该算法与DP算法得到的最佳油耗相比仍有差距。Danil^[5]提出基于神经网络的控制策略, 通过扩展卡尔曼滤波器和同步扰动随机逼近方法实现神经网络离线和在线训练方法的有效结合, 但该方法计算复杂, 不同工况的节油效果差异较大。王庆年等^[6]提出的瞬时最优控制算法需要根据不同工况离线计算分离因子, 但却可以获得比基于发动机最优曲线控制更好的燃油经济性。

Vinot等^[7]将基于Bellman最优化原理的动态规划算法用于PRIUS的节油效果分析和评价, 在已知道路工况的条件下, 通过计算每个时间和状态网格下的代价函数可以得到能量分配的全局最优解。Paganelli等^[8]将发动机实际燃油消耗和电池等效燃油消耗之和定义为目标代价函数, 提出等效燃油消耗最小策略(Equivalent consumption minimization strategy, ECMS)。Skugor等^[9]将基于规则的控制算法和等效燃油消耗目标函数相结合, 通过在发动机高效运行区内搜索最优工作点, 提高了算法的控制性能。但从优化理论可知, ECMS只能实现瞬时燃油消耗最小, 并不能获得全局最优的控制效果。

针对现有能量管理策略不能同时兼顾实时性和最优性的问题, 本文提出一种基于二次型最优控制理论的能量优化管理策略。该策略通过建立以电池组剩余能量为状态变量, 以电池组有效输出功率为控制变量的线性数学模型, 将PRIUS动力系统的能量管理问题处理为二次型最优跟踪问题, 最终得到由增益为常数矩阵的状态反馈控制和指令前馈控制构成的控制律。利用ADVISOR软件二次开发的仿真模型, 在不同道路工况条件下进行仿真实验, 结果表明, 能量优化管理策略不仅计算量小, 而且能在保证车辆驾驶性能的同时通过优化功率分配达到降低整车油耗的控制效果。

1 车辆模型

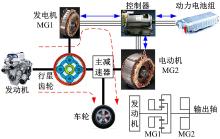
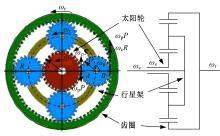
PRIUS混合动力汽车搭载的THS(Toyota hybrid system)动力系统采用行星齿轮构成混联式拓扑结构, 该系统结构紧凑、体积小, 具有较高的传动效率。如图1所示, THS动力系统由电池组、发动机、发电机MG1、电动机MG2、控制器和行星齿轮等组成。其中, 行星齿轮与动力源相连构成功率耦合驱动, 并将发动机的动力输出分成两部分, 一部分直接传递到输出轴, 另一部分则通过发电机转化为电能, 根据控制策略的需求, 这部分电能用于给电池组充电, 或驱动电机以满足整车动力需求。显然, 从瞬时优化角度看, 动力输出通过机械路径传递效率要更高, 但将电池组存储的电能在未来合适工况条件下使用, 则更有利于提高整体节油效果。

	Figure Option View Download New Window
	图1 THS动力系统结构示意图Fig.1 Powertrain configuration of THS

1.1 非线性数学模型

根据汽车动力学原理, 车辆在行驶过程中必须克服来自路面的滚动阻力、空气阻力和上坡行驶的坡度阻力, 其动力学方程可表示为:

$\begin{matrix} F (t) \cdot η_{t} = δm \frac{dv (t)}{dt} + mg f_{r} cosθ + mgsinθ + \frac{1}{2} ρ C_{D} A v^{2} (t) \end{matrix}$ （1）

式中:η _t为动力系统效率; δ 为汽车旋转质量换算系数, δ > 1; m为汽车总质量; v(t)为实际车速; f_r为滚动阻力系数; θ 为道路坡度角; ρ 为空气密度; C_D为空气阻力系数; A为迎风面积。

在式(1)两侧同时乘以车速v(t), 得到车辆的功率平衡方程为:

$P_{req} (t) \cdot η_{t} = \frac{1}{2} δm \frac{d v^{2} (t)}{dt} + mg f_{r} v (t) cosθ + mgv (t) sinθ + \frac{1}{2} ρ C_{D} A v^{3} (t)$ （2）

式中:P_req(t)为车辆需求功率。

在不超过电池组最大充放电功率的限制条件下, P_req(t)由发动机的有效输出功率P_ice(t)和电池组有效输出功率P_bat(t)共同提供, 满足:

$\begin{matrix} P_{req} (t) = P_{ice} (t) + P_{bat} (t) \end{matrix}$ （3）

PRIUS的电池组采用镍氢蓄电池, 其充放电过程是复杂的电化学反应过程, 很难建立精确的数学模型, 本文利用等效电压源与电池内阻构成的内阻模型模拟其工作特性。

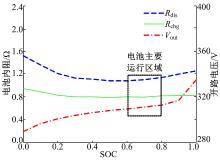	Figure Option View Download New Window
	图2 电池组开路电压和内阻特性图Fig.2 Characteristics of open-circuit-voltage and internal resistance for battery package

如图2所示, 电池开路电压V_out和内阻R_int均是与SOC有关的函数, 且在同一荷电状态下, 充电电阻R_chg和放电电阻R_dis的数值不同。当SOC在0.6~0.8之间变化时, 电池组充放电效率较高, 开路电压和内阻值的变化很小, 可近似认为是常值^[10]。此时电池组的动态特性可描述为:

$\begin{matrix} \frac{dSOC (t)}{dt} \cdot E = - \frac{V_{out} (V_{out} - \sqrt[]{V_{out}^{2} - 4 R_{int} P_{bat} (t)})}{2 R_{int}} \end{matrix}$ （4）

式中:E为电池组的总能量, E· SOC(t)为电池组的剩余能量。

1.2 线性数学模型

THS动力系统选用的发电机MG1和电动机MG2均为永磁无刷直流电机, 具有宽广的弱磁调速范围和高效工作区, 且电机效率对发动机工作点不敏感。取 $\begin{matrix} {\bar{η}}_{MG 1} \end{matrix}$ 和 $\begin{matrix} {\bar{η}}_{MG 2} \end{matrix}$ 分别为MGs对应的电机系统平均效率, 则电池组有效输出功率P_bat(t)可表示为:

$\begin{matrix} P_{bat} (t) = P_{MG 1} (t) {\bar{η}}_{MG 1}^{k_{1}} + P_{MG 2} (t) {\bar{η}}_{MG 2}^{k_{2}} \end{matrix}$ （5）

式中:P_MGs(t)< 0表示电机MGs处于发电状态, 反之处于电动状态; 参数k_s取1代表电机工作于发电模式, k_s取-1代表电机工作于电动模式。

$\begin{matrix} η_{bat} = \frac{P_{bat} (t)}{(\frac{V_{out} (V_{out} - \sqrt[]{V_{out}^{2} - 4 R_{int} P_{bat} (t)})}{2 R_{int}})} \end{matrix}$ （6）

根据式(6)计算电池组功率和电池SOC分别在[-15 kW, 15 kW]和[0.6, 0.8]范围内变化时的效率, 再取其平均值作为电池组充放电平均效率, 可得:

$\begin{matrix} {\bar{η}}_{bat} \end{matrix}$ = $\begin{matrix} \{\begin{matrix} 0.8976, P_{bat} > 0 \\ 0.9459, P_{bat} \leq 0 \end{matrix} \end{matrix}$

对于具有明确物理意义的二次型性能指标, 线性二次型最优控制理论能通过对被控对象的线性模型进行求解, 得到具有统一解析形式的状态线性反馈控制律, 为此需对式(4)所示的模型进行线性化处理, 得:

$\begin{matrix} \frac{dSOC (t)}{dt} \cdot E = - \frac{P_{bat} (t)}{{\bar{η}}_{bat}^{n}} = - \frac{P_{MG 1} (t) {\bar{η}}_{MG 1}^{k_{1}} + P_{MG 2} (t) {\bar{η}}_{MG 2}^{k_{2}}}{{\bar{η}}_{bat}^{n}} \end{matrix}$ （7）

式中:参数n取1代表电池处于放电状态, n取-1代表电池处于充电状态。

车辆行驶过程中, 通过车速传感器即可测得当前时刻的车速v(t), 转矩需求根据驾驶员的踏板指令计算得到, 此时需求功率P_req(t)可视作已知量。由式(3)可知, 当P_req(t)已知时, P_ice(t)可由P_bat(t)唯一确定。考虑式(7)所示的线性模型, 将其表示为线性状态空间方程为:

$\begin{matrix} \{\begin{matrix} \overset{\cdot}{x} (t) = Ax (t) + Bu (t) \\ y (t) = Cx (t) \end{matrix} \end{matrix}$ （8）

式中:x(t)=E· SOC(t)为状态变量; u(t)=P_bat(t)为控制变量; A=0; B=-1/ $\begin{matrix} {\bar{η}}_{bat}^{n} \end{matrix}$ ; C=1。1.3 约束条件

在给定的时间区间[t₀, t_f]中, 发动机有效输出功率P_ice(t)和电池组有效输出功率P_bat(t)应满足以下约束条件:

$0 \leq P_{ice} (t) \leq P_{ice_max}$ （9）

$P_{bat_min} \leq P_{bat} (t) \leq P_{bat_max}$ （10）

式中:P_{ice_max}为发动机的最大输出功率; P_{bat_min}和P_{bat_max}分别为动力电池组的最大充电功率和最大放电功率。

为保证电池组具有足够的充放电容量和较高的效率, 电池荷电状态SOC(t)应满足:

$l o_{soc} \leq SOC (t) \leq h i_{soc}$ （11）

$\frac{|SOC (t_{f}) - SO C_{req}|}{SO C_{req}} < 3 %$ （12）

式中:lo_soc为电池SOC的最低限值; hi_soc为电池SOC的最高限值; SOC_req为电池SOC的期望值。

本文使用线性数学模型只为得到用于能量优化的反馈控制律, 仿真时使用的被控对象仍是如式(2)和式(4)所示的实际非线性对象。

2 能量优化管理策略

经过对THS系统模型的线性化处理, 其能量优化管理问题可简化为只和电池SOC相关的单自由度优化控制问题, 即寻找最优控制量u^*(t), 使系统能够从初始状态x(t₀)转移到终端状态x(t_f), 并使系统的性能成本函数J最小。二次型最优控制理论通过构造具有鲜明物理意义的性能指标, 得到具有简单且统一解析表达形式的最优解, 并可通过状态反馈(和指令前馈)实现闭环最优控制, 是一种有效解决混合动力汽车能量优化管理问题的方法。

本文将THS系统能量优化管理的控制目标设计为:在满足车辆驾驶动力性和平稳性的前提下, 保证发动机、电池组有效输出功率和电池SOC的波动维持在一定的范围内, 从而间接降低整车燃油消耗值。为此构造如下二次型性能指标:

$J_{2} = \frac{1}{2} \int_{t_{0}}^{t_{f}} [γ_{1} {(x (t) - x^{*})}^{2} + γ_{2} P_{ice}^{2} (t) + γ_{3} P_{bat}^{2} (t)] dt$ （13）

式中:x^*=E· SOC_req为电池组的能量期望值; 第一项γ ₁ $\begin{matrix} {(x (t) - x^{*})}^{2} \end{matrix}$ 用于限制电池组剩余能量相对于期望值的波动范围, 以保证其始终能够辅助发动机进行驱动或回收车辆的制动能量; 第二项γ ₂ $\begin{matrix} P_{ice}^{2} \end{matrix}$ (t)和第三项γ ₃ $\begin{matrix} P_{bat}^{2} \end{matrix}$ (t)用于抑制发动机有效输出功率和电池组有效输出功率的波动范围。

将式(3)代入式(13), 则二次型性能指标可重新表示为:

$J_{2} = \frac{1}{2} \int_{t_{0}}^{t_{f}} [γ_{1} {(x (t) - x^{*})}^{2} + γ_{2} {(P_{req} (t) - P_{bat} (t))}^{2} + γ_{3} P_{bat}^{2} (t)] dt$

$\begin{matrix} = \frac{1}{2} \int_{t_{0}}^{t_{f}} [\frac{}{} γ_{1} {(x (t) - x^{*})}^{2} + (γ_{2} + γ_{3}) \cdot {(P_{bat} (t) - \frac{γ_{2}}{γ_{2} + γ_{3}} P_{req} (t))}^{2} + \frac{γ_{2} γ_{3}}{γ_{2} + γ_{3}} P_{req}^{2} (t)] dt \end{matrix}$ （14）

由于车辆需求功率P_req(t)是已知量, 因此只需对式(14)中的前两项进行优化即可, 性能指标化简为:

$J_{2} = \frac{1}{2} \int_{t_{0}}^{t_{f}} [\frac{}{} γ_{1} {(x (t) - x^{*})}^{2} + (γ_{2} + γ_{3}) \cdot {(P_{bat} (t) - \frac{γ_{2}}{γ_{2} + γ_{3}} P_{req} (t))}^{2}] dt$ （15）

对于如式(15)所示的二次型性能指标, 取系统控制误差变量e $\begin{matrix} (t) \end{matrix}$ =x $\begin{matrix} (t) \end{matrix}$ -x^*, 若令

$u^{' (t)} = P_{bat} (t) - \frac{γ_{2}}{γ_{2} + γ_{3}} P_{req} (t)$ （16）

则有

$J_{2} = \frac{1}{2} \int_{t_{0}}^{t_{f}} [Q e^{2} (t) + Ru'^{2} (t)] dt$ （17）

式中:Q=γ ₁; R=γ ₂+γ ₃为可调权重系数。

显然, 由式(8)和式(17)构成一个二次型最优跟踪问题, 当性能指标中的终端时间t_f固定时, 系统的最优控制律应为:

$\begin{matrix} u' (t) = - R^{- 1} B^{T} [K (t) x (t) - g (t)] \end{matrix}$ (18)

式中:K(t)为下述黎卡提矩阵微分方程的唯一解; g(t)为伴随向量。

$\{\begin{matrix} \overset{\cdot}{K} (t) = - K (t) A - A^{T} K (t) + \\ K (t) B R^{- 1} B^{T} K (t) - C^{T} QC \\ K (t_{f}) = 0 \end{matrix}$ （19）

$\{\begin{matrix} \overset{\cdot}{g} (t) = - [A - B R^{- 1} B^{T} K {(t)]}^{T} g (t) - C^{T} Qz (t) \\ g (t_{f}) = 0 \end{matrix}$ （20）

通常而言, K(t)和g(t)应在预先已知指令信号z(t)在[t₀, t_f]内的信息后通过离线计算得到, 但在笔者之前的研究中^[11]已通过仿真试验证明:当终端时间t_f足够大(但有限)时, K(t)在区间[t₀, t_f]中除去在t_f附近的一小段时间外, 均为常值K, 且满足代数黎卡提方程:

$\begin{matrix} KA + A^{T} K - KB R^{- 1} B^{T} K + Q = 0 \end{matrix}$ （21）

对于常值给定z(t)=x^*, g(t)在区间[t₀, t_f]中除去在t_f附近一小段时间外均为常值g, 且满足:

$\begin{matrix} {[A - B R^{- 1} B^{T} K]}^{T} g + C^{T} Q x^{*} = 0 \end{matrix}$ （22）

由于A-BR^-¹B^TK为稳定矩阵, 因此有

$\begin{matrix} g = - {[(A - B R^{- 1} B^{T} {K)}^{T}]}^{- 1} C^{T} Q x^{*} \end{matrix}$ （23）

将式(21)(23)求解得到的K和g代入式(18), 得到常值指令x^*下的最优控制律为:

$u^{' (t)} = - R^{- 1} B^{T} Kx (t) - R^{- 1} B^{T} {[(A - B R^{- 1} B^{T} {K)}^{T}]}^{- 1} C^{T} Q x^{*}$ (24)

为了避免发动机在低效率区工作, 能量优化管理策略还在电机驱动/回收制动模式和混合驱动模式间设置控制律切换点P₀, 当需求功率P_req(t)≤ P₀且SOC(t)满足式(11)要求时, 系统运行在电机驱动/回收制动模式, 由电池组提供车辆的驱动功率(0≤ P_req(t)≤ P₀), 或对制动能量进行回收(P_req(t)< 0)。当P_req(t)> P₀时, 系统运行在混合驱动模式, 此时发动机启动运行, 电池组作为能量缓冲器, 避免因工况变化导致发动机的输出功率大幅波动。

在计及模式切换的条件下, 能量优化管理策略可表示为:

$\begin{matrix} \{\begin{matrix} P_{bat} (t) = \{\begin{matrix} P_{req} (t), \\ P_{req} (t) \leq P_{0} \\ - R^{- 1} B^{T} Kx (t) - R^{- 1} B^{T} [(A - \\ B R^{- 1} B^{T} {K)}^{T}]^{- 1} C^{T} Q x^{*} + \\ \frac{γ_{2}}{γ_{2} + γ_{3}} P_{req} (t), \\ P_{req} (t) > P_{0} \end{matrix} \\ P_{ice} (t) = P_{req} (t) - P_{bat} (t) \end{matrix} \end{matrix}$ （25）

由式(25)可以看出, 本文提出的能量优化管理策略选定合适的控制参数后, 无需再根据道路工况进行动态调整, 且最终得到的控制律只与当前时刻的车辆需求功率P_req(t)、电池组剩余能量x(t)和能量期望值x^*有关, 是一种可在工况未知条件下应用的控制策略, 极具工程应用价值。

3 仿真模型

美国国家再生能源实验室(NREL)开发的ADVISOR软件具有仿真模型模块化、源代码开放化、仿真环境可视化以及建模方式多样化的特点, 能实现对能量管理策略的验证、评估与优化, 因此在诸多国内外的研发机构中得到广泛应用。

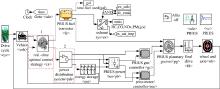
本文提出的能量优化管理策略, 其核心思想是根据当前时刻的系统状态和给定的期望值直接计算最优控制律, 无需通过后向路径逐级计算动力源的功率需求值, 因此ADVISOR软件原有的混合仿真方法已不满足该策略的仿真要求。本文以软件内PRIUS混合动力汽车仿真模型为参考, 按照新的仿真要求在Matlab/Simulink语言环境下进行系统的二次开发, 重新搭建车辆的正向仿真模型, 如图3所示。

在车辆行驶过程中, 驾驶员的踏板指令被解释为转矩指令, 通过不断调整踏板给定, 使其能够沿给定的道路工况行驶。为模拟该驾驶过程, 在整车仿真模型中, 由道路工况模块(Drive cycle)根据选定的工况给出期望车速r(t), 结合反馈的实际车速v(t), 由式(2)所示的功率平衡方程得到车辆需求功率P_req(t)。控制策略单元通过内置的优化控制算法模块, 根据电池组剩余能量x(t)、能量期望值x^*以及车辆需求功率P_req(t), 由式(25)所示的优化控制律得到发动机有效输出功率P_ice(t)和电池组有效输出功率P_bat(t)。

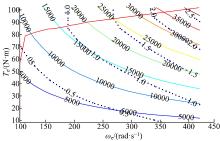
由于电动机MG2与主减速器直接相连, 其转速由当前车速直接决定, 此时为使发动机能沿如图4所示的最优工作曲线运行, 仿真模型一方面根据发动机有效输出功率P_ice(t)对发动机节气门和发电机MG1的转速进行联调; 另一方面调节电动机MG2的转矩, 使发电机MG1和电动机MG2的输出功率之和等于电池组有效输出功率P_bat(t)。该控制过程首先由控制策略单元利用线性查表插值方法, 在最优工作曲线上确定P_ice(t)对应的最优工作点[ $\begin{matrix} T_{ice}^{opt} \end{matrix}$ (t), $\begin{matrix} ω_{ice}^{opt} \end{matrix}$ (t)], 再由功率分配单元根据电池组有效输出功率P_bat(t)和发动机最优工作点分别确定发电机MG1的转速指令值 $\begin{matrix} ω_{MG 1}^{opt} \end{matrix}$ (t)和电动机MG2的转矩指令值 $\begin{matrix} T_{MG 2}^{opt} \end{matrix}$ (t)。

	Figure Option View Download New Window
	图3 采用能量优化管理策略的ADVISOR仿真模型Fig.3 ADVISOR simulation model using energy optimization strategy

	Figure Option View Download New Window
	图4 PRIUS混合动力汽车发动机最优工作曲线Fig.4 Optimal operating line(OOL)of PRIUS HEV engine

发动机、发电机MG1和电动机MG2在不超过各单元自身功率限制的前提下, 分别给出实际能够提供的转速和转矩值, 并通过行星齿轮单元(planetary gearset)的动力分配和主减速器单元(final drive)的速比变换, 最终由车轮/驱动轴单元(wheel and axle)求得当前时刻的实际车速。将其作为仿真输入回传到整车模块, 此时正向通道的仿真计算完成, 仿真模型开始下一时刻的仿真计算。

下面将重点对重新设计开发的控制策略单元(图3虚线框1所示)和功率分配单元(图3虚线框2所示)的内部结构予以说明。

3.1 控制策略单元

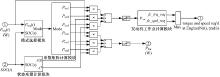
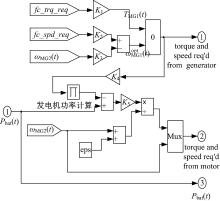
从上述分析可知, 控制策略单元是仿真模型的核心, 其输入分别为整车单元计算得到的需求功率P_req(t)和电池组单元提供的SOC实测值SOC(t), 内部结构如图5所示。根据P_req(t)和电池SOC的不同, 首先由模式选择模块确定THS系统的运行模式mode(t), 如前所述, 可分为以下两种。

(1)电机驱动/回收制动模式

当P_req(t)≤ P₀且SOC(t)满足式(11)要求时, 发动机不参与工作, 由电池组提供车辆的驱动功率或对制动能量进行回收。为使发动机的有效输出功率P_ice(t)→ 0, 需调节式(13)所示性能指标中的权重系数γ ₂→ ¥ , 则此时有P_bat(t)→ P_req(t)。

(2)混合驱动模式

发动机启动运行, 电池组作为能量缓冲器, 可以避免发动机输出功率随道路工况变化而大幅频繁变化, 使其保持在高效区域内运行。

在状态变量计算模块内设定电池组能量期望值x^*=0.7× 6(A)× 308(V)× 3600(s), 并将电池组SOC实测值SOC(t)转化为表1控制量矩阵计算中所需的状态变量x(t)。然后, 控制策略单元根据系统选定的运行模式, 利用系数矩阵计算模块提供的权系数和黎卡提方程的解(如表1所示), 分别计算当前时刻的发动机有效输出功率P_ice(t)和电池组有效输出功率P_bat(t)。P_bat(t)经过限幅后直接作为电池组和功率分配单元的输入, 而P_ice(t)则需通过发动机工作点计算模块确定其最优工作点。图4所示的最优工作曲线预先以数据表形式存储于模块内, 当THS系统工作在混合驱动模式时, 通过线性查表插值的方法可得到P_ice(t)对应的最优工作点[ $\begin{matrix} T_{ice}^{opt} \end{matrix}$ (t), $\begin{matrix} ω_{ice}^{opt} \end{matrix}$ (t)]。

	Figure Option View Download New Window
	图5 控制策略单元仿真框图Fig.5 Block simulation diagram of control strategy

表1 不同运行模式下的权系数和黎卡提方程的解 Table 1 Weight coefficient and solutions of Riccati algebraic equation in different operation modes

运行模式	权系数	控制量矩阵	黎卡提方程的解
电机驱动/回收制动模式	γ ₂→ ¥	$\begin{matrix} [\begin{matrix} P_{ice} (t) \\ P_{bat} (t) \end{matrix}] \end{matrix}$ = $\begin{matrix} [\begin{matrix} 0 \\ P_{req} (t) \end{matrix}] \end{matrix}$	—
混合驱动模式	γ ₁=0.01, γ ₂=2, γ ₃=2	$\begin{matrix} [\begin{matrix} P_{ice} (t) \\ P_{bat} (t) \end{matrix}] \end{matrix}$ = $\begin{matrix} [\begin{matrix} \frac{γ_{3}}{γ_{2} + γ_{3}} P_{req} (t) + \frac{bK}{γ_{2} + γ_{3}} x (t) - \frac{γ_{1}}{bK} x^{} \\ \frac{γ_{2}}{γ_{2} + γ_{3}} P_{req} (t) - \frac{bK}{γ_{2} + γ_{3}} x (t) + \frac{γ_{1}}{bK} x^{} \end{matrix}] \end{matrix}$	K=0.162 g=-0.05x^*

表1 不同运行模式下的权系数和黎卡提方程的解 Table 1 Weight coefficient and solutions of Riccati algebraic equation in different operation modes

为模拟发动机实际工作状态, 模块内还引入怠速限制, 即

(1)当 $\begin{matrix} ω_{ice}^{opt} \end{matrix}$ (t)≥ fc_spd_idle(怠速值)时, 有

$\begin{matrix} \{\begin{matrix} fc_trq_req (t) = T_{ice}^{opt} (t) \\ fc_spd_req (t) = ω_{ice}^{opt} (t) \end{matrix} \end{matrix}$ （26）

(2)当 $\begin{matrix} ω_{ice}^{opt} \end{matrix}$ (t)< fc_spd_idle时, 有

$\begin{matrix} \{\begin{matrix} fc_trq_req (t) = \frac{P_{ice} (t)}{fc_spd_idle} \\ fc_spd_req (t) = fc_spd_idle \end{matrix} \end{matrix}$ （27）

3.2 功率分配单元

THS系统的行星齿轮机构由太阳轮、行星架和齿圈三部分组成, 如图6所示^[12]。发电机MG1与太阳轮相连, 发动机与行星架相连, 电动机MG2及输出传动轴与齿圈相连。设太阳轮啮合半径为S, 齿圈啮合半径为R, λ =R/S为齿圈与太阳轮的半径比或齿数比, 则行星齿轮各元件间的关系可表示为:

$\begin{matrix} \{\begin{matrix} ω_{MG 1} (t) = (1 + λ) ω_{ice} (t) - λ ω_{MG 2} (t) \\ T_{MG 1} (t) = - \frac{1}{1 + λ} T_{ice} (t) \\ ω_{r} (t) = ω_{MG 2} (t) \\ T_{r} (t) = T_{MG 2} (t) + \frac{λ}{1 + λ} T_{ice} (t) \end{matrix} \end{matrix}$ （28）

式中:ω _ice、ω _MG1、ω _MG2、ω _r分别为发动机、发电机MG1、电动机MG2和齿圈的转速输出值; T_ice、T_MG1、T_MG2、T_r分别为发动机、发电机MG1、电动机MG2和齿圈的转矩输出值。

	Figure Option View Download New Window
	图6 行星齿轮结构示意图Fig.6 Structure diagram of planetary gear mechanism

为充分利用THS系统的无级调速功能, 如图7所示, 功率分配单元通过对发动机节气门、发电机MG1的转速和电动机MG2的转矩进行联调, 实现发动机在最优工作曲线上平滑运行的控制要求。

	Figure Option View Download New Window
	图7 功率分配单元仿真框图Fig.7 Block diagram of power distribution simulation

当已知实际车速v(t)时, 考虑主减速器的影响, 行星齿轮齿圈转速ω _r(t)满足:

$\begin{matrix} ω_{r} (t) = \frac{G_{r}}{r_{w}} v (t) \end{matrix}$ （29）

式中:G_r为主减速器速比; r_w为车轮半径。

由于电动机MG2与齿圈直接相连, 其实际转速ω _MG2(t)与齿圈转速ω _r(t)相等, 此时根据确定的发动机最优工作点[ $\begin{matrix} T_{ice}^{opt} \end{matrix}$ (t), $\begin{matrix} ω_{ice}^{opt} \end{matrix}$ (t)], 利用式(28)可得发电机MG1的转速指令值 $\begin{matrix} ω_{MG 1}^{opt} \end{matrix}$ (t)。

为使发电机MG1和电动机MG2的输出功率之和等于电池组有效输出功率P_bat(t), 需要同步调节电动机MG2的转矩, 使其满足:

$\begin{matrix} T_{MG 2}^{opt} (t) = \frac{P_{bat} (t) - T_{MG 1} (t) \cdot ω_{MG 1}^{opt} (t) \cdot η_{MG 1}^{k_{1}}}{ω_{MG 2} (t) \cdot η_{MG 2}^{k_{2}}} \end{matrix}$ （30）

4 仿真结果分析

PRIUS混合动力汽车的基本参数如下:发动机(FC_PRIUS_JPN)排量为1.5 L, 最大功率为43 kW@4000 r/min, 最大转矩为102 N· m@4000 r/min; 电池(ESS_NIMH6)额定容量/电压为6 A· h/308 V; 发电机MG1(GC_PRIUS_JPN)最大功率为15 kW; 电机MG2(MC_PRIUS_JPN)最大功率为31 kW; 迎风面积为1.746 m²; 空气阻力系数为0.3; 滚动阻力系数为0.009; 汽车总质量为1368 kg。本文选择NEDC工况作为标准测试工况, 该工况分为市区工况和市郊工况。其中, 市区工况由4个市区运转循环单元组成, 最高车速50 km/h, 平均车速19 km/h, 行驶里程4.052 km; 市郊工况最高车速120 km/h, 平均车速62.6 km/h, 行驶里程6.955 km。

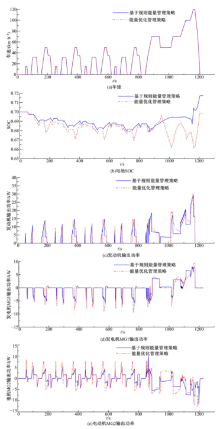
本文将能量优化管理策略的仿真结果与PRIUS量产车中使用的基于规则的能量管理策略^[2]进行对比, 设电池组SOC初始值SOC_init=0.7, 控制律切换点P₀=5 kW, 得到仿真结果如图8所示。

	Figure Option View Download New Window
	图8 NEDC工况下的仿真结果Fig.8 Simulation results under NEDC driving cycle

如图8所示, 能量优化管理策略可以满足车辆动力性能要求, 与道路工况给定的期望车速相比, 其平均追踪误差仅为0.064 m/s, 且电池组SOC在末端时刻与给定期望值的偏差仅为0.17%, 完全满足式(12)所示约束条件的要求。缩短发动机运行时间和减少启停次数是有效降低车辆油耗的重要手段, NEDC工况的仿真结果表明, 在能量优化管理策略的控制下, 发动机的实际运行时间仅为370 s, 与基于规则的能量管理策略相比, 减少运行时间126 s, 并减少2次发动机启停过程。

本文选择的发动机在输出功率9 kW≤ P_ice≤ 20 kW时, 具有较高的燃油经济性。数据分析表明, 在NEDC的市区和市郊两种工况条件下, 能量优化管理策略控制的发动机平均输出功率分别为10.35 kW和12.85 kW, 比基于规则能量管理策略分别提高44.35%和29.67%。此外, 以标准差作为发动机输出功率波动情况的衡量指标, 在NEDC的市区和市郊两种工况条件下, 能量优化管理策略的发动机输出功率标准差分别为2.92 kW和5.61 kW, 比基于规则能量管理策略分别减少10.7%和12.6%。综上所述, 与量产PRIUS中使用的基于规则能量管理策略相比, 本文提出的策略能够随着道路工况的变化主动调节发电机MG1和电动机MG2的输出功率, 避免发动机输出功率大幅波动, 从而达到节能降耗的目标。

研究表明, 当电池荷电状态小范围变化时, 基于PMP控制策略中的协态变量λ 近似为常值, 使用该方法与动态规划得到的燃油消耗基本一致^[11], 即油耗最小值。以基于PMP的全局最优控制策略为基准, 在不同道路工况条件下, 对基于规则能量管理策略和能量优化管理策略的油耗及末端时刻t_f的电池SOC值进行对比, 结果见表2。

仿真数据表明, 尽管道路工况差异较大, 但能量优化管理策略仍能获得与基于PMP的全局最优控制策略相接近的节油效果, 其中, 在INDIA_HWY工况下, 二者的油耗之差仅为3.4%; 油耗之差最大的情况发生在UDDS工况, 为8.97%。同样, 与基于PMP的全局最优控制策略相比, PRIUS量产车中使用基于规则能量管理策略的节油效果最佳的情况发生在NEDC工况下, 油耗之差为8.95%; 而在INDIA_URBAN工况下, 二者之间的油耗之差则高达19.7%。对比结果显示, 本文提出的能量优化管理策略在不同道路工况条件下都能获得更优的节油效果, 且该过程仅依靠优化发动机和动力电池组的输出功率即可实现。

表2 不同道路工况油耗及SOC(t_f)结果 Table 2 Fuel consumption results and SOC(t_f) of different driving cycle

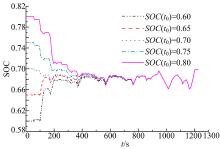
同样选择NEDC工况作为标准测试工况, 当电池组SOC的初值不同时, 取SOC(t₀)={0.6, 0.65, 0.7, 0.75, 0.8}, 如图9所示, 在末端时刻t_f, 电池SOC仍能保证回到期望值附近, 这说明本文提出的能量优化管理策略对于不同的电池初始荷电状态同样具有很强的适应性。

	Figure Option View Download New Window
	图9 不同SOC(t₀)在NEDC工况下的SOC变化曲线Fig.9 SOC trajectories with various SOC(t₀) under NEDC driving cycle

5 结束语

基于二次型最优控制理论提出了一种新的能量优化管理策略, 该策略得到的控制律是关于PRIUS混合动力汽车动力系统当前状态和指令信号的函数, 并能够根据车辆实际运行状态和道路工况实时调整以适应行驶环境的变化, 是一种易于工程应用的能量管理策略。为了对策略的有效性进行验证, 文中选择目前广泛使用的ADVISOR车辆仿真软件, 利用二次开发技术重新搭建满足能量优化管理策略仿真要求的模型, 并在不同道路工况下进行仿真对比实验。结果表明:与PRIUS中使用的基于规则能量管理策略相比, 本文所提策略具有更好的节油效果, 且该策略对于不同的道路工况和电池初始荷电状态均有较好的适应性。在不需要提前预知工况的前提下, 该策略不仅可以保证驾驶的动力性, 而且可以获得与基于PMP的全局最优控制策略相近的节油效果, 因此可以作为一种近似替代全局最优控制策略的方法指导未来的实际工程开发。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	项昌乐, 韩立金, 刘辉, 等. 混联混合动力车辆功率分流耦合机构特性分析[J]. 汽车工程, 2010, 32(3): 183-187. Xiang Chang-le, Han Li-jin, Liu Hui, et al. An analysis on the characteristics of power-split and coupling mechanism in series/parallel HEV[J]. Automotive Engineering, 2010, 32(3): 183-187. [本文引用:1]
[2]	Liu J M, Peng H, Filipi Z. Modeling and analysis of the toyota hybrid system[C]//Proc of the 2005 IEEE/ASME International Conf on Adv Intelligent Mechatronics, Monterey, CA, 2005: 134-139. [本文引用:2]
[3]	Kim J, Kang J, Choi W, et al. Control algorithm for a power split type hybrid electric vehicle[C]//2010 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Piscataway, NJ, 2010: 1575-1580. [本文引用:1]
[4]	Chen Z, Mi C C. An adaptive online energy management controller for power-split HEV based on dynamic programming and fuzzy logic[C]//Vehicle Power and Propulsion Conference, Dearborn, MI, 2009: 335-339. [本文引用:1]
[5]	Danil V P. Toyota PRIUS HEV neurocontrol[C]//Proc of International Joint Conf on Neural Networks, Orland o, FL, 2007: 2129-2134. [本文引用:1]
[6]	王庆年, 王文, 王鹏宇, 等. 基于瞬时效率的功率分流式混合动力汽车最佳分离因子的确定[J]. 吉林大学学报: 工学版, 2013, 43(5): 1160-1164. Wang Qing-nian, Wang Wen, Wang Peng-yu, et al. Determination of the best separation factor for power-split hybrid electric vehicle based on instantaneous efficiency[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1160-1164. [本文引用:1]
[7]	Vinot E, Trigui R, Yuan C, et al. Improvement of an EVT-based HEV using dynamic programming[J]. IEEE Transactions on Vehicular Technology, 2014, 63(1): 40-50. [本文引用:1]
[8]	Paganelli G, Delprat S, Guerra T M, et al. Equivalent consumption minimization strategy for parallel hybrid powertrains[C]//IEEE Vehicular Technology Conference, Birmingham, AL, 2002: 2076-2081. [本文引用:1]
[9]	Skugor B, Deur J, Cipek M, et al. Design of a power-split hybrid electric vehicle control system utilizing a rule-based controller and an equivalent consumption minimization strategy[J]. Proc of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2014, 228(6): 631-648. [本文引用:1]
[10]	Kim N, Cha S, Peng H. Optimal control of hybrid electric vehicles based on Pontryagin's Minimum Principle[J]. IEEE Transactions on Vehicular Technology, 2011, 19(5): 1279-1287. [本文引用:1]
[11]	夏超英, 张聪. 混合动力系统能量管理策略的实时优化控制算法[J]. 自动化学报, 2015, 41(3): 508-517. Xia Chao-ying, Zhang Cong. Real-time optimization control algorithm of energy management strategy for hybrid electric vehicles[J]. Acta Automatica Sinica, 2015, 41(3): 508-517. [本文引用:2]
[12]	赵晓静, 武一民, 王海霞. 丰田PRIUS混合动力传动系统分析与建模[J]. 机械传动, 2010, 34(6): 31-35. Zhao Xiao-jing, Wu Yi-min, Wang Hai-xia. Analysis and modeling on Toyota hybrid powertrain system[J]. Journal of Mechanical Transmission, 2010, 34(6): 31-35. [本文引用:1]

2010

0.0

. 2010, 32(3):183-187

An analysis on the characteristics of power-split and coupling mechanism in series/parallel HEV

混联混合动力车辆功率分流耦合机构特性分析

Xiang Chang-le , Han Li-jin , Liu Hui

项昌乐, 韩立金, 刘辉

分析了功率分流耦合机构的转速与转矩关系,在此基础上推导了功率分流比例与传动比和行星排特性参数的关系,研究了不同功率电机所能实现的传动比变化范围,和耦合装置效率随传动比变化的规律.最后分析了带功率分流耦合机构的车辆在起步、匀速行驶和加速等工况下的驱动特性,为功率分流混合动力车辆关键部件的参数匹配和整车控制策略的制定提供了参考. Abstract： The relationship between speed and torque of power split and coupling mechanism is analyzed. Based on this, the relation between power split ratio, drive ratio and the characteristic parameters of planetary gear set is derived, and the variation range of drive ratio the electric motor with different power can attain as well as the changing law of coupling device efficiency with drive ratio are studied. Finally the driving characteristics of vehicle with power split and coupling mechanism at starting, cruising and acceleration conditions are analyzed, providing references for working out the parameters matching of key components and vehicle control strategy.

... PRIUS(普锐斯)是丰田汽车公司最早商业化生产的混合动力汽车,它采用行星排式混联拓扑结构,成功实现了发动机和车轮之间转速和转矩的双解耦^[1] ...

2005

0.0

... PRIUS在量产车中采用基于规则的控制策略解决车辆能量协调控制的问题,根据节气门开度和电池荷电状态(State of charge,SOC)将系统运行模式分为3种,即发动机独立工作模式、电动机独立工作模式和混合工作模式,通过动力分配机构调节和控制能量流动途径,使发动机和电机在高效率区内工作^[2] ...

... 本文将能量优化管理策略的仿真结果与PRIUS量产车中使用的基于规则的能量管理策略^[2]进行对比,设电池组SOC初始值SOC_init=0 ...

2010

0.0

... 近年来,各国研究者针对PRIUS的混联拓扑结构提出多种新的能量管理策略,如Kim等^[3]提出的策略是利用发动机实际转速和目标转速之差对发电机转速进行PI控制,而电动机则根据整车需求提供转矩补偿 ...

2009

0.0

... Chen等^[4]提出基于模糊逻辑的在线自适应控制策略,该策略首先通过动态规划(Dynamic programming,DP)算法得到指定工况下的最优解,然后根据发动机与车辆需求功率的比值和电池SOC等变量建立隶属度函数及模糊规则,结果表明,即使对于选定工况,该算法与DP算法得到的最佳油耗相比仍有差距 ...

2007

0.0

... Danil^[5]提出基于神经网络的控制策略,通过扩展卡尔曼滤波器和同步扰动随机逼近方法实现神经网络离线和在线训练方法的有效结合,但该方法计算复杂,不同工况的节油效果差异较大 ...

2013

0.0

. 2013, 43(5):1160-1164 DOI:doi:10.7964/jdxbgxb201305002

Determination of the best separation factor for power-split hybrid electric vehicle based on instantaneous efficiency

基于瞬时效率的功率分流式混合动力汽车最佳分离因子的确定

Wang Qing-nian , Wang Wen , Wang Peng-yu

王庆年, 王文, 王鹏宇

This paper describes a three-step iteration method for determining the best separation factor of power-split hybrid electric vehicle based on system instantaneous efficiency. The function of the relationship between the best separation factor and the vehicle speed and power demand is obtained. Then the instantaneous optimal control algorithm of power-split hybrid electric vehicles is developed based on the best separation factor. As compared to the control algorithm based on the engine optimal curve, economical efficiency of the instantaneous optimal control algorithm based on optimal separation factor of system is improved significantly.

介绍一种基于系统瞬时效率优化的功率分流式混合动力汽车最佳分离因子的三重迭代确定方法。得到最佳分离因子与车速和需求功率的函数关系,并基于最佳分离因子开发出功率分流式混合动力汽车的瞬时最优控制算法。与基于发动机最优曲线控制算法相比,基于最佳分离因子的系统瞬时最优控制算法经济性有明显的提高。

... 王庆年等^[6]提出的瞬时最优控制算法需要根据不同工况离线计算分离因子,但却可以获得比基于发动机最优曲线控制更好的燃油经济性 ...

2014

0.0

... Vinot等^[7]将基于Bellman最优化原理的动态规划算法用于PRIUS的节油效果分析和评价,在已知道路工况的条件下,通过计算每个时间和状态网格下的代价函数可以得到能量分配的全局最优解 ...

2002

0.0

... Paganelli等^[8]将发动机实际燃油消耗和电池等效燃油消耗之和定义为目标代价函数,提出等效燃油消耗最小策略(Equivalent consumption minimization strategy,ECMS) ...

2014

0.0

... Skugor等^[9]将基于规则的控制算法和等效燃油消耗目标函数相结合,通过在发动机高效运行区内搜索最优工作点,提高了算法的控制性能 ...

2011

0.0

... 8之间变化时,电池组充放电效率较高,开路电压和内阻值的变化很小,可近似认为是常值^[10] ...

2015

0.0

. 2015, 41(3):508-517 DOI:doi:10.16383/j.aas.2015.c140119

Real-time optimization control algorithm of energy management strategy for hybrid electric vehicles

混合动力系统能量管理策略的实时优化控制算法

Xia Chao-ying , Zhang Cong.

夏超英, 张聪

Energy management strategies of hybrid electric vehicles (HEVs) based on the optimal control theory are strongly related to future driving conditions and can not solve the real-time problems of algorithms. This paper finds a new way to construct a quadratic performance index combined with rules to restrict frequent large fluctuations of the engine power, so as to indirectly reduce the fuel consumption. On the basis of the approximate linearization of HEV systems, the quadratic optimal tracking theory is utilized to derive a constant feedback control law. The control power of the engine and the motor are expressed as linear functions of current system states and commands, and then applied to the nonlinear HEV. Simulation results show that this real-time control algorithm can achieve a good oil-saving effect,and can adapt to various typical driving cycles and initial battery state of charge values.

依据最优控制理论得到的混合动力汽车能量管理策略与未来的驾驶需求相关联,无法解决算法的实时性问题.本文另辟蹊径,结合规则构造二次型性能指标来限制发动机功率的大幅度频繁波动,间接地降低油耗.为此,在对混合动力系统近似线性处理的基础上,利用二次型最优跟踪理论推导出定常的反馈控制律,将发动机和电机功率表示成系统当前状态和车速指令的线性函数并应用于非线性实车系统.仿真结果表明,本文提出的能量管理实时控制算法可以达到良好的节油效果, 对不同的道路工况和电池初始荷电状态有良好的适应性.

... 通常而言,K(t)和g(t)应在预先已知指令信号z(t)在[t₀,t_f]内的信息后通过离线计算得到,但在笔者之前的研究中^[11]已通过仿真试验证明:当终端时间t_f足够大(但有限)时,K(t)在区间[t₀,t_f]中除去在t_f附近的一小段时间外,均为常值K,且满足代数黎卡提方程: ...

... 近似为常值,使用该方法与动态规划得到的燃油消耗基本一致^[11],即油耗最小值 ...

2010

0.0

. 2010, 34(6):31-35 DOI:doi:10.3969/j.issn.1004-2539.2010.06.009

Analysis and modeling on Toyota hybrid powertrain system

丰田PRIUS混合动力传动系统分析与建模

Zhao Xiao-jing , Wu Yi-min , Wang Hai-xia.

赵晓静, 武一民, 王海霞

混合动力汽车传动系统的建模是混合动力汽车传动系统能量控制策略开发、仿真和优化的基础.对比分析了三代丰田PRIUS混合动力传动系统的结构和基本工作原理,建立了传动系统发动机、动力分离装置、电动/发电机和动力用蓄电池等各子系统模型,基于统一的动力传动系统结构建立了丰田PRKIS混合动力传动系统的运动学、动力学和能量守恒模型.

... 2 功率分配单元THS系统的行星齿轮机构由太阳轮、行星架和齿圈三部分组成,如图6所示^[12] ...