混合动力汽车凸极式永磁同步电机电流解耦控制

引用本文

王伟华, 穆嘉毅, 符容, 范永凯, 王文楷. 混合动力汽车凸极式永磁同步电机电流解耦控制. 吉林大学学报(工学版), 2017, 47(3): 693-700
WANG Wei-hua, MU Jia-yi, FU Rong, FAN Yong-kai, WANG Wen-kai. Current decouple control of salient-pole permanent magnet synchronous motor for hybrid electric vehicle. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 693-700 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703001
Permissions

混合动力汽车凸极式永磁同步电机电流解耦控制

王伟华, 穆嘉毅, 符容, 范永凯, 王文楷

吉林大学汽车仿真与控制国家重点实验室,长春 130022

作者简介:王伟华(1971-),男,教授,博士.研究方向:节能与新能源汽车.E-mail:wwh_jlu@126.com

基金项目:“863”国家高技术研究发展计划项目(2011AA11A224)

摘要

针对电机旋转坐标系下直轴与交轴电流耦合的问题,采用对角矩阵解耦控制方法,通过在电机的电流环中增加一个解耦器矩阵,将励磁电流 i_d与转矩电流 i_q解耦成互不干扰的量,保证电机输出转矩的精准性。仿真试验结果表明:与前馈解耦控制方法、反馈解耦控制方法相比,该方法在电机转速较高或电机参数发生变化时,鲁棒性更好,解耦效果显著。

关键词: 车辆工程; 混合动力汽车; 凸极式永磁同步电机; 电流解耦; 对角矩阵解耦控制

中图分类号:U469 文献标志码:A 文章编号:1671-5497(2017)03-0693-08

Current decouple control of salient-pole permanent magnet synchronous motor for hybrid electric vehicle

WANG Wei-hua, MU Jia-yi, FU Rong, FAN Yong-kai, WANG Wen-kai

State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

Abstract

For the coupling problems of d-axis and q-axis currents in the synchronous rotating frame, the diagonal matrix decoupling control method is proposed. The field current i_d and torque current i_q are decoupled into no-interfering variables by increasing a decoupling compensator in the motor current loop, so as to ensure the accuracy of PMSM's output torque. Furthermore, this method is compared with the feedforward decoupling control method and the feedback decoupling method. It is shown that the proposed method has better robustness and decoupling effect when the motor speed is high or the motor parameters change.

Key words: vehicle engineering; hybrid electric vehicle; salient-pole permanent magnet synchronous motor(SPMSM); current decoupling; diagonal matrix decoupling control

Show Figures

0 引言

在混合动力汽车动态协调控制中, 电机除输出自身期望转矩外, 还会对发动机转矩不足进行补偿, 保证整车总转矩不发生大的波动^{[1, 2]}。

对于凸极式永磁同步电机(Salient-pole permanent magnet synchronous motor, SPMSM)系统, 电流环作为内环, 其优劣关系到整个电机驱动系统的准确性和快速性, 特别是在转矩控制方面, 转矩精确性控制的关键在于电流的控制。通常, 传统意义上的PID控制器优势在于简单、易实现, 但在电机数学模型中其只对同步旋转d、q坐标系中两轴各自的电流环进行控制, 而忽略了两者的交叉耦合项。交叉耦合项会对转矩产生干扰, 无法保证电机的动态性能, 所以很难使永磁同步电机实现高精准控制^[3]。故需要对电机电流进一步解耦, 而解耦控制的研究重点集中于控制器的研究。传统解耦控制方法, 如前馈解耦控制^[4]、反馈解耦控制^[5], 通过在控制器输入端施加负耦合电压消除电流间的耦合问题, 严重依赖于电机参数且不能完全解耦, 双PI解耦控制方法^[6]、交叉耦合控制方法^{[7, 8]}利用增加两个额外的PI控制实现解耦控制; 自适应解耦控制方法^{[9, 10]}将耦合项作为可测扰动, 采用自动校正的控制方法对耦合进行动、静态补偿, 并对补偿器参数进行优化, 实质上要求在线辨识对象模型, 适应能力差且鲁棒性不强; 智能解耦控制方法可以实现线性和非线性系统的在线精确解耦, 包括神经网络解耦控制^{[11, 12, 13]}、滑模解耦控制^{[14, 15, 16]}等, 但此解耦方法稳定性和收敛性的证明还待进一步研究。总之, 在实际工程中, 上述方法算法太复杂且难以实现较好的解耦。此外, 外界因素(如电机参数的变化、外部扰动、搭建模型的局限性等)的干扰也会使电机的动态性能受到很大影响^[17], 故找寻简单、易行且有效的解耦控制方法势在必行^[9]。

基于此, 本文提出了一种简单、易行的解耦控制方法— — 对角矩阵解耦控制方法, 并将该方法用于凸极式永磁同步电机。该方法考虑了反电动势, 建立了更精确的电机控制模型, 消除了d、q轴的耦合问题, 能够在动、静态过程中均获得准确的、完全的解耦, 且不增加硬件设备。

1 电机电流耦合现象

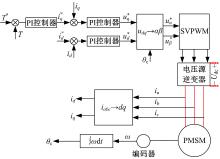
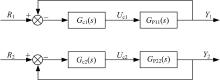
如图1所示, 电机采用矢量控制方法, 经过Park变化后, 虽将电流i_d与i_q完全解耦, 但在实际电流环控制中, 控制量u_d与u_q并没有完全解耦, 两者依然存在着交叉耦合部分。此外, 耦合项(ω _sL_qi_q)和(ω _sL_di_d+ω _sψ _f)均与转子角频率ω _s以及电感参数L_q有关, 若转速或电感参数发生变化, 耦合电压也会随之发生变化, 故此, 励磁电流i_d与转矩电流i_q的耦合影响更严重。关于电机电流耦合问题, 可从凸极式永磁同步电机的电压方程(1)中看出:

$\{\begin{array}{l} u_{d} = R_{s} i_{d} + L_{d} \frac{d i_{d}}{d t} - ω_{s} L_{q} i_{q} \\ u_{q} = R_{s} i_{q} + L_{q} \frac{d i_{q}}{d t} + ω_{s} L_{d} i_{d} + ω_{s} ψ_{f} \end{array}$ (1)

式中:ψ _f为电机永磁体磁链。

	Figure Option View Download New Window
	图1 永磁同步电机的矢量控制系统Fig.1 Vector control system of PMSM

2 电机电流解耦控制方法

常用的解决凸极式永磁同步电机控制系统中交叉耦合项问题的方法有前馈解耦控制和反馈解耦控制, 这两种方法在电机参数发生变化时解耦效果较差, 故本文采用对角矩阵解耦控制方法^[18]。

2.1 前馈解耦控制方法

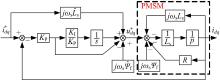
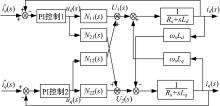
依据电压方程式(1), 在输入电压u_d、u_q上分别加入耦合电压项(-ω _sL_q $i_{q}^{*}$ )和(ω _sL_d $i_{d}^{*}$ +ω _sψ _f), 那么耦合电压就会消除, 电机解耦即可实现。前馈解耦框图如图2所示。

	Figure Option View Download New Window
	图2 永磁同步电机前馈解耦控制图Fig.2 Feedforward decoupling control chart of PMSM

2.2 反馈解耦控制方法

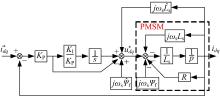
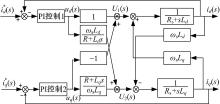
反馈解耦控制方法利用电机输出的实际电流i_dq作为控制变量, 产生耦合电压矢量进行解耦控制。由于i_dq是永磁同步电机的实际电流, 用于反馈补偿的电压项要更贴近于实际值, 这对定子电流的解耦很有利, 如图3所示。

	Figure Option View Download New Window
	图3 永磁同步电机反馈解耦控制图Fig.3 Feedback decoupling control chart of PMSM

2.3 对角矩阵解耦控制方法

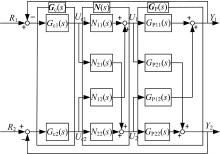
对角矩阵解耦法要求被控对象(电机)的特性矩阵与解耦矩阵相乘得到一个对角矩阵。图4为双变量解耦控制系统的框图。

	Figure Option View Download New Window
	图4 双变量解耦控制系统的控制框图Fig.4 Decoupling control block diagram of double variables system

在图4中, Y(s)=G_P(s)U(s), U(s)=N(s)U_c(s), 联合两式有:

$Y (s) = G_{P} (s) N (s) U_{c} (s)$ (2)

若式(2)为对角矩阵, 则可以实现双变量的完全解耦, 其中G(s)=G_P(s)N(s)称为解耦器矩阵, 这是对角矩阵解耦控制方法的关键。依据对角矩阵解耦设计要求, 即:

$[\begin{array}{l} G_{P 11} (s) & G_{P 12} (s) \\ G_{P 21} (s) & G_{P 22} (s) \end{array}] [\begin{array}{l} N_{11} (s) & N_{12} (s) \\ N_{21} (s) & N_{22} (s) \end{array}] = [\begin{array}{l} G_{P 11} (s) & 0 \\ 0 & G_{P 22} (s) \end{array}]$ （3）

被控对象的输出与输入变量之间应满足如下矩阵方程:

$[\begin{array}{l} Y_{1} (s) \\ Y_{2} (s) \end{array}]$ = $[\begin{array}{l} G_{P 11} (s) & 0 \\ 0 & G_{P 22} (s) \end{array}] [\begin{array}{l} U_{c 1} (s) \\ U_{c 2} (s) \end{array}]$ (4)

进而实现了解耦控制, 且解耦后的等效系统如图5所示。

	Figure Option View Download New Window
	图5 对角矩阵解耦后的系统控制框图Fig.5 Control block diagram after diagonal matrix decoupling system

由式(1)可得到对应的传递函数方程为:

$\{\begin{array}{l} U_{d} (s) = (R + L_{d} s) I_{d} (s) - ω_{s} L_{q} I_{q} (s) \\ U_{q} (s) = (R + L_{q} s) I_{q} (s) + ω_{s} L_{d} I_{d} (s) + ω_{s} ψ_{f} \end{array}$ （5）

为了解决电机电流耦合问题, 采用对角矩阵解耦控制法, 引入解耦器矩阵, 得到永磁同步电机双变量解耦控制示意图如图6所示。

	Figure Option View Download New Window
	图6 凸极式永磁同步电机双变量解耦控制示意图Fig.6 Decoupling control schematic diagram of double variables SPMSM

解耦器矩阵的求解过程如下。令u'_q=u_q-ω _sψ _f, 取如下矩阵:

$G (s) = [\begin{array}{l} G_{11} (s) & G_{12} (s) \\ G_{21} (s) & G_{22} (s) \end{array}] = [\begin{array}{l} R + L_{d} s & ω_{s} L_{q} \\ ω_{s} L_{d} & R + L_{q} s \end{array}]$ (6)

$Y (s) = [\begin{array}{l} Y_{1} (s) \\ Y_{2} (s) \end{array}] = [\begin{array}{l} I_{d} (s) \\ I_{q} (s) \end{array}]$ （7）

$U (s) = [\begin{array}{l} U_{1} (s) \\ U_{2} (s) \end{array}]$ （8）

$U_{c} (s) = [\begin{array}{l} U_{d} (s) \\ U'_{q} (s) \end{array}]$ （9）

整理式(6)~(8)可得:

$Y (s) = \frac{1}{G_{22} (s) G_{11} (s) + G_{12} (s) G_{21} (s)} \times (\begin{array}{l} G_{22} (s) & G_{12} (s) \\ - G_{21} (s) & G_{11} (s) \end{array}) U (s)$ (10)

由图6可知:

$U (s) = N (s) U_{c} (s)$ （11）

整理式(10)(11)可得:

$Y (s) = \frac{1}{G_{22} (s) G_{11} (s) + G_{12} (s) G_{21} (s)} \times (\begin{array}{l} G_{22} (s) & G_{12} (s) \\ - G_{21} (s) & G_{11} (s) \end{array}) \times (\begin{array}{l} N_{11} (s) & N_{12} (s) \\ N_{21} (s) & N_{22} (s) \end{array}) U_{c} (s)$ （12）

对角矩阵解耦控制法的设计目标为:

$Y (s) = (\begin{array}{l} \frac{1}{G_{11} (s)} & 0 \\ 0 & \frac{1}{G_{22} (s)} \end{array}) U_{c} (s)$ （13）

求解式(12)(13)可得:

$\{\begin{array}{l} N_{21} (s) = \frac{G_{21} (s)}{G_{11} (s)} \\ N_{11} (s) = \frac{G_{11} (s)}{G_{21} (s)} N_{21} (s) = 1 \\ N_{22} (s) = 1 \\ N_{12} (s) = - \frac{G_{12} (s)}{G_{22} (s)} N_{22} (s) = - \frac{G_{12} (s)}{G_{22} (s)} \end{array}$ （14）

将式(6)代入式(14)得到解耦器矩阵N(s)为:

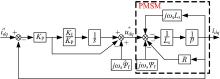
$N (s) = (\begin{array}{l} 1 & - \frac{ω_{s} L_{q}}{R + L_{q} s} \\ \frac{ω_{s} L_{d}}{R + L_{d} s} & 1 \end{array})$ （15）

综上, 三相凸极式永磁同步电机的双变量解耦控制框图如图7所示。

	Figure Option View Download New Window
	图7 凸极式永磁同步电机的双变量解耦控制框图Fig.7 Double variables decoupling control diagram of SPMSM

	Figure Option View Download New Window
	图8 凸极式永磁同步电机对角矩阵解耦控制框图Fig.8 Diagonal matrix decoupling control diagram of SPMSM

永磁同步电机对角矩阵解耦控制框图如图8所示, 对应闭环传递函数为:

$G (s) = \frac{K_{P} s + K_{I}}{s^{2} L_{s} + (R + K_{P}) s + K_{I}}$ （16）

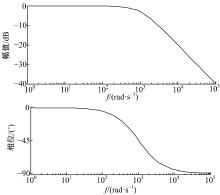
依据传递函数和伯德图(见图9)可知, 电机控制系统不再受角速度ω 的影响, 采用对角矩阵解耦控制后解耦效果良好。

	Figure Option View Download New Window
	图9 凸极式永磁同步电机伯德图Fig.9 Bode plots of SPMSM

3 仿真验证及分析

凸极式永磁同步电机采用i_d=0控制, 随着转矩电流i_q的变化, 观察分析磁链电流i_d的波动变化。运行条件:转速由0 r/min线性增加到1000 r/min, 0.08 s后达到匀速运行; 转矩在0.15 s时由0 N· m突增至0.5 N· m。此外, 由于在实际工作过程中, 永磁同步电机的参数受运行环境和工况变化的影响较频繁, 电机控制会受到一定影响, 故本文还比较了电机电感参数为原来参数的50%和150%时交、直轴电流波形的变化。

	Figure Option View Download New Window
	图10 采用前馈解耦控制时的交、直轴电流波形Fig.10 Waveform of d-axis and q-axis currents with using feedforward decoupling control

	Figure Option View Download New Window
	图11 采用反馈解耦控制时的交、直轴电流波形Fig.11 Waveform of d-axis and q-axis currents with using feedback decoupling control

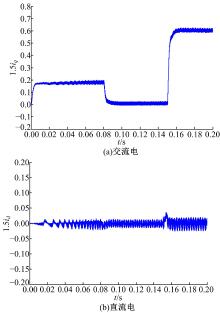
	Figure Option View Download New Window
	图12 采用对角矩阵解耦控制时的交、直轴电流波形Fig.12 Waveform of d-axis and q-axis currents with using diagonal matrix decoupling control

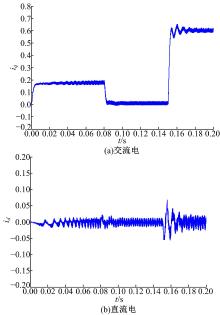
	Figure Option View Download New Window
	图13 采用前馈解耦控制且电感Ls’=50%× Ls时的交、直轴电流波形Fig.13 Waveform of d-axis and q-axis currents with using feedforward decoupling control and Ls’=50%× Ls

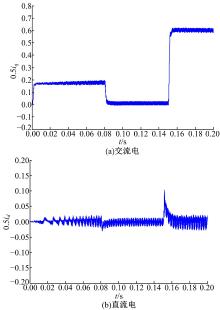
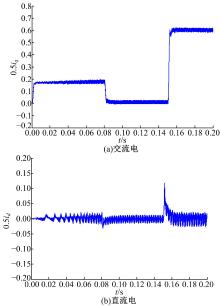	Figure Option View Download New Window
	图14 采用反馈解耦控制且电感Ls’=50%× Ls时的交、直轴电流波形Fig.14 Waveform of d-axis and q-axis currents with using feedback decoupling control and Ls’=50%× Ls

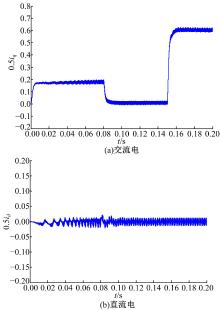	Figure Option View Download New Window
	图15 采用对角矩阵解耦控制且电感Ls’=50%× Ls 时的交、直轴电流波形Fig.15 Waveform of d-axis and q-axis currents with using diagonal matrix decoupling control and Ls’= 50%× Ls

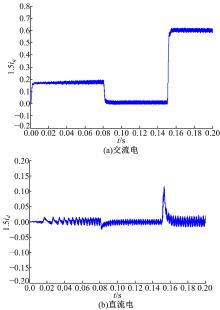	Figure Option View Download New Window
	图16 采用前馈解耦控制且电感Ls’=150%× Ls 时的交、直轴电流波形Fig.16 Waveform of d-axis and q-axis currents with using feedforward decoupling control and Ls’=150%× Ls

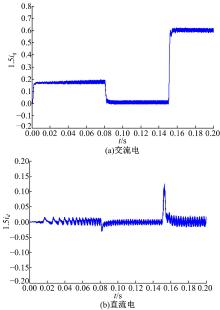	Figure Option View Download New Window
	图17 采用反馈解耦控制且电感Ls’=150%× Ls时的交、直轴电流波形Fig.17 Waveform of d-axis and q-axis currents with using feedback decoupling control and Ls’=150%× Ls

由图10~图12可知, 转矩电流i_q在0.08 s时由0.18 A突降至0.01 A, 在0.15 s时由0.01 A突增至0.6 A, 此过程中, 采用前馈解耦控制(见图10)时, 磁链电流i_d在0.08 s时瞬间下降, 0.15 s时电流突增至0.08 A; 采用反馈解耦控制(见图11)时, 磁链电流i_d在0.08 s时瞬间下降, 0.15 s时电流突增至0.1 A; 采用对角矩阵解耦控制(见图12)时, 磁链电流i_d在0.08 s时波动较小, 在0.15 s时电流波动可以忽略。由此可以看出, 采用对角矩阵解耦控制可以较好地实现磁链电流和转矩电流的解耦, 磁链电流均不会随着转速或转矩电流i_q的变化而产生波动。

图13~图15为驱动电机受到外界环境变化导致电机参数(电感)变化时, 各种解耦方法下交、直轴电流波形的变化。当电感参数变化到原来的50%时, 耦合项电压变化为原来的一半, 前馈(见图13)和反馈(见图14)解耦控制方法中解耦补偿电压与电机电感参数有关, 电流i_q变化时, i_d的波动较大。对角矩阵解耦控制方法(见图15)中由于解耦器矩阵耦合项成分减少, 导致电流波动比较小。

当电感参数变化到原来的150%时, 使得耦合项电压变化为原来的150%, 前馈(见图16)和反馈(见图17)解耦控制方法中, 解耦补偿电压与电机参数相关, 所以在转速达到稳定时, 转矩电流i_q发生突变导致磁链电流也发生了变化; 在转矩发生突变时, 转矩电流发生较大的跳动, 致使磁链电流也发生较大的波动, 即解耦受到了影响, 解耦不完全。但是, 对于对角矩阵解耦控制方法(见图18), 不论转速达到稳定还是转矩发生突变, 磁链电流均不会随着转矩电流i_q变化而产生较大波动, 可见对角矩阵解耦在电机参数变化时仍具有良好的解耦效果。

	Figure Option View Download New Window
	图18 采用对角矩阵解耦控制且电感Ls’=150%× Ls时的交、直轴电流波形Fig.18 Waveform of d-axis and q-axis currents with using diagonal matrix decoupling control and Ls’=150%× Ls

4 结束语

混合动力汽车在模式切换时电机需要对发动机转矩不足进行补偿, 基于此, 本文采用一种简单、易行的对角矩阵解耦控制方法来提高电机转矩输出精准性, 建立了凸极式永磁同步电机模型, 分析了电流耦合问题并设计了解耦器矩阵。将该方法与前馈解耦、反馈解耦效果进行对比, 结果表明, 对角矩阵解耦控制方法具有更好的鲁棒性, 系统的控制精度更高, 可以提高凸极式永磁同步电机转矩输出的精准性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Cheng Y, Trigui R, Espanet C, et al. Specifications and design of a PM electric variable transmission for Toyota Prius II[J]. IEEE Transactions on Vehicular Technology, 2011, 60(9): 4106-4114. [本文引用:1]
[2]	Chen Li, Xi Gang, Sun Jing. Torque coordination control during mode transition for a series-parallel hybrid electric vehicle[J]. IEEE Transactions on Vehicular Technology, 2012, 61(7): 2936-2949. [本文引用:1]
[3]	Luo H R, Cheng H, Wang J. A cascade linear active disturbance rejection controller for vector control system of PMSM[C]//3rd International Conference on Mechatronics, Robotics and Automation, Shenzhen, China, 2015: 1076-1082. [本文引用:1]
[4]	Fetz J, Horstmann D. Comparison of different field-orientation control methods for an induction machine fed by a PWM-modulator control for a high power three-level-inverter drive system[C]//EPE Aaschen, Orland o, Florida, 1989: 1079-1085. [本文引用:1]
[5]	Lorenz R D, Lawson D B. Performance of feedforward current regulators for field oriented induction machine controllers[J]. IEEE Transactions on Industry Applications, 1987, 23(4): 597-602. [本文引用:1]
[6]	林科振, 林飞, 杨中平. 永磁同步电机解耦控制方法研究[C]∥第七届中国高校电力电子与电力传动学术年会论文集, 北京, 中国, 2013: 287-293. Lin Ke-zhen, Lin Fei, Yang Zhong-ping. Research on decoupling control method of permanent magnet synchronous motor[C]//The 7th Symposium on Power Electronics & Electrical Drives, Beijin, China, 2013: 287-293. [本文引用:1]
[7]	周渊深. 异步电动机解耦控制策略综述[J]. 中小型电机, 2005, 32(6): 56-60, 64. Zhou Yuan-shen. Survey on decoupling control strategy for induction motor[J]. S&M Electric Machines, 2005, 32(6): 56-60, 64. [本文引用:1]
[8]	杨南方, 骆光照, 刘卫国. 误差补偿的永磁同步电机电流环解耦控制[J]. 电机与控制学报, 2011, 15(10): 50-62. Yang Nan-fang, Luo Guang-zhao, Liu Wei-guo. Decoupling control of current loop for permanent magnet synchronous motor drives using error compensation[J]. Electric Machines and Control, 2011, 15(10): 50-62. [本文引用:1]
[9]	桑保华, 薛晓中. 多变量解耦控制方法[J]. 火力与指挥控制, 2008, 32(11): 13-16. Sang Bao-hua, Xue Xiao-zhong. A summary of multivariable decoupling control methods[J]. Fire Control and Command Control, 2008, 32(11): 13-16. [本文引用:2]
[10]	王晰, 李少远. 多模型分层递阶自适应前馈解耦控制器[J]. 控制与决策, 2005, 20(1): 17-22. Wang Xi, Li Shao-yuan. Hierarchical multiple model adaptive feedforward decoupling controller[J]. Control and Decision, 2005, 20(1): 17-22. [本文引用:1]
[11]	周涌, 陈庆伟, 吴晓蓓, 等. 基于动态神经网络解耦线性化的内模控制[J]. 南京理工大学学报, 2004, 28(6): 566-570. Zhou Yong, Chen Qing-wei, Wu Xiao-bei, et al. Internal model control using dynamical neural network model and decoupling linearization[J]. Journal of Nanjing University of Science and Technology, 2004, 28(6): 566-570. [本文引用:1]
[12]	王晓哲, 顾树生. 基于遗传算法的PID神经网络解耦控制[J]. 控制与决策, 1999, 14(增刊1): 617-619. Wang Xiao-zhe, Gu Shu-sheng. A PID neural network decoupling control based on genetic algorithm[J]. Control and Decision, 1999, 14(Sup. l): 617-619. [本文引用:1]
[13]	孙晓东, 朱熀秋, 张涛, 等. 一种永磁同步电机解耦控制的新方法[J]. 微电机, 2010, 43(1): 61-65. Sun Xiao-dong, Zhu Huang-qiu, Zhang Tao, et al. A new method of decoupling control of permanent magnet-type synchronous motor[J]. Micromotors, 2010, 43(1): 61-65. [本文引用:1]
[14]	Comanescu M, Xu L Y, Batzel T D. Decoupled current control of sensorless induction-motor drives by integral sliding mode[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 3836-3845. [本文引用:1]
[15]	Zaky M S. Robust sliding mode speed controller-based model reference adaptive system (MRAS) and load torque estimator for interior permanent magnet synchronous motor (IPMSM) drives[J]. Electric Power Components and Systems, 2015, 43(13): 1523-1533. [本文引用:1]
[16]	Kommuri S K, Rath J J, Veluvolu K C, et al. Decoupled current control and sensor fault detection with second-order sliding mode for induction motor[J]. IET Control Theory & Applications, 2015, 9(4): 608-617. [本文引用:1]
[17]	祝晓辉, 李颖晖, 付明明. 永磁同步电机电流调节器动态特性分析及改进设计[J]. 电工电能新技术, 2007, 26(4): 26-30. Zhu Xiao-hui, Li Ying-hui, Fu Ming-ming. Dynamic analysis and improved design of current regulators for permanent magnet synchronous motors[J]. Advanced Technology of Electrical Engineering and Energy, 2007, 26(4): 26-30. [本文引用:1]
[18]	尤裕祥, 方昌始. 用对角矩阵法实现解耦的异步机解耦控制系统[J]. 电气自动化, 1993, 15(1): 4-7. You Yu-xiang, Fang Chang-shi. The asynchronous machine decoupling control system with using the diagonal matrix method[J]. Electrical Automation, 1993, 15(1): 4-7. [本文引用:1]

2011

0.0

... 0 引言在混合动力汽车动态协调控制中,电机除输出自身期望转矩外,还会对发动机转矩不足进行补偿,保证整车总转矩不发生大的波动^[1,2] ...

2012

0.0

... 0 引言在混合动力汽车动态协调控制中,电机除输出自身期望转矩外,还会对发动机转矩不足进行补偿,保证整车总转矩不发生大的波动^[1,2] ...

2015

0.0

... 交叉耦合项会对转矩产生干扰,无法保证电机的动态性能,所以很难使永磁同步电机实现高精准控制^[3] ...

1989

0.0

... 传统解耦控制方法,如前馈解耦控制^[4]、反馈解耦控制^[5],通过在控制器输入端施加负耦合电压消除电流间的耦合问题,严重依赖于电机参数且不能完全解耦,双PI解耦控制方法^[6]、交叉耦合控制方法^[7,8]利用增加两个额外的PI控制实现解耦控制 ...

1987

0.0

2013

0.0

. 2013, :287-293

Research on decoupling control method of permanent magnet synchronous motor

永磁同步电机解耦控制方法研究

Lin Ke-zhen , Lin Fei , Yang Zhong-ping.

林科振, 林飞, 杨中平

永磁同步电机矢量控制时,交直轴存在交叉耦合分量,会影响电机的动态性能。本文介绍了前馈解耦、反馈解耦、双PI解耦和内模解耦等四种方法的控制原理,绘制了控制框图,利用传递函数画出了系统零极点分布图和波特图,对几种方法进行了分析讨论。相比前馈解耦和反馈解耦,双PI解耦和内模解耦对电机参数变化有更好的鲁棒性。并通过matlab对几种方法进行了仿真验证。

2005

0.0

. 2005, 32(6):56-60,64

Survey on decoupling control strategy for induction motor

异步电动机解耦控制策略综述

Zhou Yuan-shen.

周渊深

2011

0.0

. 2011, 15(10):50-62 DOI:doi:10.3969/j.issn.1007-449X.2011.10.008

Decoupling control of current loop for permanent magnet synchronous motor drives using error compensation

误差补偿的永磁同步电机电流环解耦控制

Yang Nan-fang , Luo Guang-zhao , Liu Wei-guo.

杨南方, 骆光照, 刘卫国

摘　要：针对矢量控制永磁同步电机电流环在动态调节过程中的相互耦合问题，提出一种基于电流误差的多项式交叉耦合补偿方案。以一阶延迟的电流环为目标，在经典的d轴和q轴电流反馈控制结构的基础上，设计基于电流误差的交叉耦合补偿控制器，采用误差零点的Taylor展开式进行纯积分补偿结构的逼近，减小电压饱和效应，得到多项式结构的补偿控制器，并据此进行了误差讨论。相对于基本的电流反馈控制，该方案能够更有效地实现d轴和q轴电流在动态调节过程中的控制，尤其是提高加速过程中电流的跟踪性能。仿真和实验结果验证了该方案的可行性。

2008

0.0

... 自适应解耦控制方法^[9,10]将耦合项作为可测扰动,采用自动校正的控制方法对耦合进行动、静态补偿,并对补偿器参数进行优化,实质上要求在线辨识对象模型,适应能力差且鲁棒性不强 ...

... 此外,外界因素(如电机参数的变化、外部扰动、搭建模型的局限性等)的干扰也会使电机的动态性能受到很大影响^[17],故找寻简单、易行且有效的解耦控制方法势在必行^[9] ...

2005

0.0

. 2005, 20(1):17-22

Hierarchical multiple model adaptive feedforward decoupling controller

多模型分层递阶自适应前馈解耦控制器

Wang Xi , Li Shao-yuan.

王晰, 李少远

2004

0.0

. 2004, 28(6):566-570 DOI:doi:10.3969/j.issn.1005-9830.2004.06.002

Internal model control using dynamical neural network model and decoupling linearization

基于动态神经网络解耦线性化的内模控制

Zhou Yong , Chen Qing-wei , Wu Xiao-bei

周涌, 陈庆伟, 吴晓蓓

采用动态神经网络对一类多变量仿射非线性系统进行建模,利用解析求得的模型动态逆,将非线性对象近似输入输出解耦线性化.针对复合后的伪线性系统采用内模控制,分析了存在建模误差的情况下闭环系统的鲁棒稳定性.仿真表明了所提方法的有效性.

... 智能解耦控制方法可以实现线性和非线性系统的在线精确解耦,包括神经网络解耦控制^[11,12,13]、滑模解耦控制^[14,15,16]等,但此解耦方法稳定性和收敛性的证明还待进一步研究 ...

1999

0.0

. 1999, 14(增刊1):617-619

A PID neural network decoupling control based on genetic algorithm

基于遗传算法的PID神经网络解耦控制

Wang Xiao-zhe , Gu Shu-sheng.

王晓哲, 顾树生

摘　要：提出一种基于遗传算法的ＰＩＤ神经网络解耦控制算法。该算法将遗传算法用于多层前向神经网络的连接权系数的学习。克服了ＢＰ算法易陷入局部极值的缺点，并具备ＰＩＤ神经网络控制器结构简单规范、动态和静态性能良好等优点，适用于对非线性多变量系统的解耦控制。

2010

0.0

. 2010, 43(1):61-65 DOI:doi:10.3969/j.issn.1001-6848.2010.01.016

A new method of decoupling control of permanent magnet-type synchronous motor

一种永磁同步电机解耦控制的新方法

Sun Xiao-dong , Zhu Huang-qiu , Zhang Tao

孙晓东, 朱熀秋, 张涛

针对永磁同步电机这一多变量、非线性、强耦合的控制对象,提出了一种基于神经网络在线辨识的永磁同步电机逆系统解耦控制新方法.通过静态神经网络加积分器来构造永磁同步电机的逆系统,并在实际运行中不断地修正神经网络权值,使其更精确地逼近逆系统.将逆系统与永磁同步电机原系统复合成两个伪线性子系统,使永磁同步电机解耦成二阶线性转速子系统和一阶线性磁链子系统,在此基础上,运用线性系统理论进行综合.仿真试验表明这种控制策略能够实现永磁同步电机转速和定子磁链之间的动态解耦控制,并且系统具有良好的动静态性能.

2008

0.0

2015

0.0

2015

0.0

2007

0.0

. 2007, 26(4):26-30 DOI:doi:10.3969/j.issn.1003-3076.2007.04.007

Dynamic analysis and improved design of current regulators for permanent magnet synchronous motors

永磁同步电机电流调节器动态特性分析及改进设计

Zhu Xiao-hui , Li Ying-hui , Fu Ming-ming.

祝晓辉, 李颖晖, 付明明

建立了永磁同步电机复矢量模型,应用复矢量根轨迹法和复矢量频域分析法对复平面等价形式的永磁同步电机电流调节器性能进行了研究.使用以基频为中心一定带宽内频率响应状况及抗扰强度函数的方法对电流调节器性能进行了分析,结果表明建立在同步坐标系内一般形式的比例-积分电流调节器性能随着外部干扰及基波频率升高而恶化.采用基于小波多尺度解析的PI调节器技术对其进行改进设计,理论分析及仿真结果表明,改进后的电流调节器较之传统的调节器具有较好的抑制噪声及抗干扰的能力.

1993

0.0

. 1993, 15(1):4-7

The asynchronous machine decoupling control system with using the diagonal matrix method

用对角矩阵法实现解耦的异步机解耦控制系统

You Yu-xiang , Fang Chang-shi.

尤裕祥, 方昌始

摘　要：

... 2 电机电流解耦控制方法常用的解决凸极式永磁同步电机控制系统中交叉耦合项问题的方法有前馈解耦控制和反馈解耦控制,这两种方法在电机参数发生变化时解耦效果较差,故本文采用对角矩阵解耦控制方法^[18] ...