可变刚度和阻尼的半主动馈能悬架隔振性能

引用本文

王军年, 叶涛, 孙文, 王庆年. 可变刚度和阻尼的半主动馈能悬架隔振性能. 吉林大学学报(工学版), 2017, 47(3): 701-708
WANG Jun-nian, YE Tao, SUN Wen, WANG Qing-nian. Vibration isolation performance of energy-regenerative semi-active suspension with variable stiffness and damping. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 701-708 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703002
Permissions

可变刚度和阻尼的半主动馈能悬架隔振性能

王军年¹, 叶涛², 孙文¹, 王庆年¹

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.新加坡国立大学机械工程系,新加坡 117575

作者简介:王军年(1981-),男,副教授,博士.研究方向:汽车系统动力学,电动汽车驱动理论及关键技术.E-mail:wjn@jlu.edu.cn

基金项目:国家自然科学基金项目(51205153); 吉林省自然科学基金项目(20140101072JC)

摘要

首先,以单自由度1/4车辆模型为研究对象,对其地面激励和外力激励幅频特性进行分析。然后,基于天棚控制方法设计了开关阻尼控制算法,定义了9种控制模式。最后,以正弦激励和随机激励作为输入,采用Matlab/Simulink进行性能仿真对比分析,结果表明:两个阻尼器都是on-off状态对应的工作模式,可以使悬架系统表现出良好的隔振性能。

关键词: 车辆工程; 可变刚度和阻尼; 半主动悬架; 开关阻尼控制

中图分类号:U469.7 文献标志码:A 文章编号:1671-5497(2017)03-0701-08

Vibration isolation performance of energy-regenerative semi-active suspension with variable stiffness and damping

WANG Jun-nian¹, YE Tao², SUN Wen¹, WANG Qing-nian¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.Department of Mechanical Engineering, National University of Singapore, Singapore 117575,Singapore

Abstract

The vibration isolation performance of energy-regenerative semi-active suspension with variable stiffness and damping is investigated. A quarter car model with one degree of freedom with semi-active suspension model is used as the research subject. First, the magnitude frequency response characteristics of the model to road bumpiness excitation and external force excitation are analyzed. Then, a simple switch on-off damping control algorithm is designed based on the skyhook control method. Nine different on/off control modes are defined subsequently. Finally, with the input of sinusoidal function and random vibration, the control performances are simulated and compared using Matlab/Simulink. The results show that the control modes, which have on-off status for both variable dampers, lead the suspension to have excellent performance of vibration isolation.

Key words: automotive engineering; variable stiffness anddamping; semi-active suspension; on/off damping control

Show Figures

0 引言

悬架系统对整车行驶平顺性、操纵稳定性等具有重大影响。悬架系统可以分为被动悬架、半主动悬架以及主动悬架。被动悬架是传统的全机械结构, 具有结构简单、性能可靠、成本低、无需额外能量注入等优点, 因而应用最为广泛, 但因悬架特性参数无法改变, 故无法兼顾各种路面乘坐舒适性和操纵稳定性要求。主动悬架包含一系列复杂的机械和电气化结构, 通过额外注入作动力可以主动改变悬架的刚度和阻尼, 自适应各种行驶路面, 最大限度地改善整车行驶平顺性和操纵稳定性, 但其能量消耗大、成本极高且结构复杂, 同时主动悬架还使整车质量增加, 因此现阶段主动悬架在汽车工业的运用还比较少^[1]。半主动悬架一般用无源但参数有级或无级可调的被动元件(弹性元件或阻尼元件)替代执行机构的主动元件, 能够改善乘坐舒适性和操纵稳定性^[2], 其性能好于被动悬架, 在控制品质上接近于主动悬架, 且结构简单、无需作动源、能量损耗小, 成本远低于主动悬架, 因而是今后悬架系统的主要发展方向和值得推广的新兴技术。一些学者研究了一些基本的主动和半主动阻尼调节结构及其对应的控制算法^{[3, 4, 5]}, 例如用磁流变液减振器实现车身振动抑制^[6], 此外, 还研究了一些基本结构的刚度调节结构及其对应的控制策略^[7], 但研究性能可靠、调节方便、既能实时变刚度又能变阻尼的半主动系统及与其对应的简单、有效的控制算法仍然很有必要^{[8, 9]}。Liu等^[8]采用两组磁流变阻尼器与弹簧并联再串联的方式组成一种变刚度和阻尼的悬架模型, 并以单自由度半主动系统为研究对象, 建立了3种不同的开关阻尼控制策略, 实现了刚度和阻尼的实时调节。国内学者也提出了一种可变刚度和阻尼的半主动悬架模型, 并探讨了相应的模糊控制策略^[9]或PID控制策略^[10]的控制效果。

本文提出了一种新型的具备馈能功能的可变刚度和阻尼的半主动悬架结构, 在简化数学模型分析的基础上, 提出了9种开关阻尼控制模式, 采用Matlab/Simulink仿真计算得出悬架的动挠度以及轮胎的动载荷数值, 并对比了典型道路条件输入下各控制模式对车辆驾驶平顺性及操纵稳定性的影响。

1 悬架结构

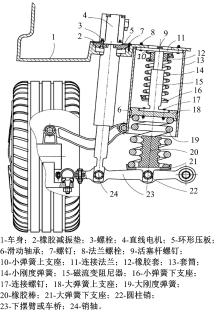
本文提出的新型可变刚度和阻尼的半主动悬架结构如图1所示。

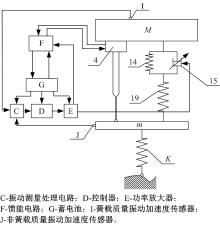
	Figure Option View Download New Window
	图1 半主动悬架结构图Fig.1 Configuration of semi-active suspension

如图1所示, 该半主动悬架主要由悬架变刚度机构和变阻尼机构组成。悬架变刚度机构包括并联在一起的小刚度弹簧14、磁流变阻尼器15以及通过下支座18将其串联在一起的大刚度弹簧19; 变阻尼机构为直线电机4。悬架变刚度机构和变阻尼机构并联布置在簧载质量(车身)和非簧载质量(车轮与下摆臂)之间。图2为其带有控制系统的简化物理模型, 其中M为簧载质量; m为非簧载质量; K为轮胎刚度。

	Figure Option View Download New Window
	图2 半主动悬架简化物理模型Fig.2 Simplified physical model of semi-active suspension

如图2所示, 直线电机4通过馈能电路F连接蓄电池G, 馈能电路主要包括整流滤波电路和双向DC/DC变换器等原件, 用于将由直线电机充当馈能减振器吸收的振动能量转化而成的电能进行整形变压后存储起来, 再次循环利用, 给磁流变阻尼器15提供电能^[11]。悬架控制器D通过振动测量处理电路C采集车身、车轮的振动加速度传感器I和J的信号, 通过天棚控制方法将控制信号通过功率放大器E驱动后有级控制直线电机4的再生制动力以及磁流变阻尼器15的阻尼力, 从而实现可变刚度和阻尼的功能。为了降低控制的复杂度和实时性要求, 直线电机和磁流变减振器采用多种工作模式分级控制, 以适应各种行驶路况。为便于分析, 利用单自由度振动(即忽略轮胎刚度K, 只考虑悬架部分)1/4车辆模型对其进行进一步动力学分析。

2 悬架系统数学模型

本文以单自由度1/4车辆半主动悬架系统为研究对象, 建立简化后的模型如图3(a)所示。该模型由两个可变阻尼器(阻尼器1和阻尼器2, 其对应的阻尼系数分别为c₁和c₂)和两个刚度不变弹簧(弹簧1和弹簧2, 对应的刚度系数分别为k₁和k₂)组成。阻尼器2和弹簧2并联后再与弹簧1串联。两个弹簧的刚度系数k₁和k₂是不可变的, 但是通过改变阻尼器2的阻尼值c₂, 就可以改变该悬架的系统刚度。如果阻尼器2的阻尼系数足够小, 整个系统的刚度近似等于弹簧1和弹簧2的串联刚度k₁k₂/(k₁+k₂); 如果阻尼器2的阻尼系数足够大, 整个系统刚度近似等于弹簧1的刚度k₁。

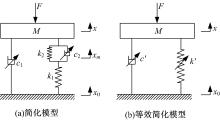	Figure Option View Download New Window
	图3 可变刚度和阻尼的半主动悬架1/4车辆模型Fig.3 1/4 vehicle model using semi-active suspension with variable stiffness and damping

图3(a)中, x、x_m、x₀分别为簧载质量M的位移、弹簧阻尼元件串联点位移以及地面位移; F为由发动机振动等外部振动产生的激励力。

根据牛顿第二定律和相关的振动理论可对图3(a)所示模型建立如下动力学方程式:

$\overset{\cdot \cdot}{Mx}$ +c₁ $(\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0})$ +k₁ $(x_{m} - x_{0})$ =-F (1)

k₂ $(x - x_{m})$ +c₂ $(\overset{\cdot}{x} - {\overset{\cdot}{x}}_{m})$ =k₁ $(x_{m} - x_{0})$ (2)

式中: $\overset{\cdot}{x}$ 、 ${\overset{\cdot}{x}}_{m}$ 、 ${\overset{\cdot}{x}}_{0}$ 分别为簧载质量M的速度、弹簧阻尼元件串联点速度和地面速度; $\overset{\cdot \cdot}{x}$ 为簧载质量M的加速度。

当只考虑地面激励, 即F=0时, 对式(1)(2)进行拉普拉斯变换(初始条件都设为0), 可得:

X(s)/X₀(s)=[c₁c₂s²+(k₁c₁+k₂c₁+k₁c₂)s+k₁k₂]/[Mc₂s³+(Mk₁+Mk₂+c₁c₂)s²+(k₁c₁+k₂c₁+k₁c₂)s+k₁k₂] (3)

令s=jω , 可得:

X(ω )/X₀(ω )=[k₁k₂-c₁c₂ω ²+j(k₁c₁+k₂c₁+k₁c₂)ω ]/[k₁k₂-(Mk₁+Mk₂+c₁c₂)ω ²+j(k₁c₁+k₂c₁+k₁c₂-Mc₂ω ²)ω ] (4)

同理, 只考虑力激励, 即x₀=0时, 有:

X(s)/F(s)=-(k₁+k₂+c₂s)/[Mc₂s³+(Mk₁+Mk₂+c₁c₂)s²+(k₁c₁+k₂c₁+k₁c₂)s+k₁k₂] (5)

令s=jω , 可得:

X(ω )/F(ω )=[-(k₁+k₂)-jc₂ω ]/[k₁k₂-(Mk₁+Mk₂+c₁c₂)ω ²+j(k₁c₁+k₂c₁+k₁c₂-Mc₂ω ²)ω ] (6)

图3(b)为3(a)所示模型对应的等效简化模型。图中, k'、c'分别为悬架系统的等效刚度系数和等效阻尼系数。如果对图3(b)所示模型运用牛顿第二定律和相关的振动理论, 其动力学方程式为:

$M \overset{\cdot \cdot}{x} + c' (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0}) + k' (x - x_{0}) = - F (7)$

当只考虑地面激励, 即F=0时, 对式(5)进行拉普拉斯变换, 可得:

$\frac{X (s)}{X_{0} (s)} = \frac{c' s + k'}{M s^{2} + c' s + k'}$

令s=jω , 可得:

$\frac{X (ω)}{X_{0} (ω)} = \frac{k' + j c' ω}{(k' - M ω^{2}) + j c' ω}$ （8）

同理, 只考虑力激励, 即x₀=0时, 对式(7)进行拉普拉斯变换, 可得:

$\frac{X (s)}{F (s)}$ = $\frac{- 1}{M s^{2} + c' s + k'}$

令s=jω , 可得:

$\frac{X (ω)}{F (s)} = \frac{- 1}{(k' - M ω^{2}) + j c' ω}$ （9）

将式(8)(9)分别与式(4)(6)进行比较, 可得:

$k' = \frac{k_{1}^{2} k_{2} + k_{2}^{2} k_{1} + k_{1} c_{2}^{2} ω^{2}}{{(k_{1} + k_{2})}^{2} + c_{2}^{2} ω^{2}}$ （10）

$c' = \frac{k_{1}^{2} c_{1} + k_{2}^{2} c_{1} + 2 c_{1} k_{1} k_{2} + c_{1} c_{2}^{2} ω^{2} + k_{1}^{2} c_{2}}{{(k_{1} + k_{2})}^{2} + c_{2}^{2} ω^{2}}$ （11）

由式(10)(11)可以看出:k'与c₁无关, 与c₂有关; c'与c₁、c₂都有关。①当c₂=¥ 时, k'=k₁(即弹簧1的刚度), c'=c₁; ②当c₂=0时, k'=k₁k₂/(k₁+k₂)(即弹簧1与弹簧2的串联刚度), c'=c₁。

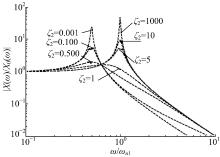
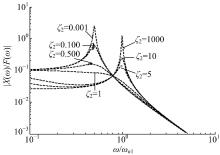
令弹簧1的固有频率ω _n₁= $\sqrt[]{k_{1} / M}$ ; 阻尼器1的阻尼比ζ ₁=c₁/(2 $\sqrt[]{M k_{1}}$ ); 阻尼器2的阻尼比ζ ₂=c₂/(2 $\sqrt[]{M k_{2}}$ )。并设M=1 kg; k₁=4π ² N/m; k₂/k₁=1/3; ζ ₁=0.01。用Matlab分别计算式(4)(6)表述的幅频特性, 结果如图4和图5所示。图4为地面位移输入下的簧载质量位移幅频特性。图5为力输入下的簧载质量位移幅频特性。

	Figure Option View Download New Window
	图4 地面激励的幅频响应Fig.4 Magnitude response of road bumpiness excitation in frequent domain

	Figure Option View Download New Window
	图5 力激励的幅频响应Fig.5 Magnitude response of engine force excitation in frequent domain

由图4和图5可以看出, 当ζ ₂较小(即ζ ₂< 1)时, 在频率较小时系统发生共振; 当ζ ₂较大(ζ ₂> 1)时, 在频率较大时发生共振。可见共振频率与ζ ₂的选择息息相关。

3 控制方法

本文控制方法采用简便、可靠的天棚控制方法。通过天棚控制方法实现调控阻尼较为简单, 即合理选择参数就能够很好地抑制车身的垂直振动、俯仰和侧倾运动, 提高车辆操纵稳定性和平顺性^[1]。基于天棚控制方法设计了开关阻尼控制算法, 可变阻尼器的开关阻尼控制算法用到了绝对速度和相对速度, 阻尼器1和阻尼器2产生的阻尼力分别为:

$f_{d 1} = \{\begin{array}{l} - c_{1_on} (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0}), if (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0}) \overset{\cdot}{x} \geq 0 \\ - c_{1_off} (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0}), if (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0}) \overset{\cdot}{x} < 0 \end{array}$ （12）

$f_{d 2} = \{\begin{array}{l} - c_{2_on} (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{m}), if (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0}) \overset{\cdot}{x} \geq 0 \\ - c_{2_off} (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{m}), if (\overset{\cdot}{x} - {\overset{\cdot}{x}}_{0}) \overset{\cdot}{x} < 0 \end{array}$ （13）

式中:c₁_{_}_on为对应可变阻尼器1为on状态时的大阻尼系数; c₁_{_}_off为对应可变阻尼器1为off状态时的小阻尼系数; c₂_{_}_on为对应可变阻尼器2的on状态时的大阻尼系数; c₂_{_}_off为对应可变阻尼器2的off状态时的小阻尼系数。

需要注意的是, 由于可变阻尼器1采用的是直线电机, 这种馈能减振器是通过滚珠丝杠将悬架的直线运动转化为电机的旋转运动, 系统中旋转部件在悬架加、减速直线运动过程中, 会由于惯量产生惯性力叠加到阻尼力f_d₁上^[12]。而本文为分析简便, 此处忽略惯性力对悬架阻尼力的影响。

由于工程上普遍采用简便高效的“ 0-1” 开关控制实现分级可调阻尼, 为此本文根据阻尼器1和阻尼器2的开关状态组合, 制定了9种控制模式。表1列出了9种阻尼开关控制模式。

表1 9种控制模式 Table 1 Nine kinds of control mode

表1中:“ off” 代表阻尼器关闭, 此时阻尼器阻尼系数为小阻尼系数c_{i_}_off, “ on” 代表阻尼器开启, 此时阻尼器阻尼系数为大阻尼系数c_{i_}_on, 其中i=1, 2代表可调阻尼器1和可调阻尼器2; “ on-off” 为阻尼器开启和关闭连续交替切换状态。具体9种类型控制模式的指示名称和含义如下所示。

类型1:阻尼器1和阻尼器2均为off状态, 系统阻尼小、刚度小, 称这种情况为软悬架系统(soft)。

类型2:阻尼器1为off状态, 阻尼器2为on状态, 系统阻尼小、刚度大, 称其为硬悬架系统(stiff)。

类型3:阻尼器1为on状态, 阻尼器2为off状态, 称之为小阻尼系统(low)。

类型4:阻尼器1和阻尼器2均为on状态, 对应大阻尼系统(high)。

类型5:阻尼器1为on-off状态, 阻尼器2为off状态, 称之为D on-off(soft)系统。

类型6:阻尼器1为on-off状态, 阻尼器2为on状态, 称之为D on-off(stiff)系统。

类型7:阻尼器1为off状态, 阻尼器2为on-off状态, 称之为S on-off(low)系统。

类型8:阻尼器1为on状态, 阻尼器2为on-off状态, 称之为S on-off(high)系统。

类型9:阻尼器1和阻尼器2均为on-off状态, 称之为D+S on-off系统。

类型1、2、3、4相当于一种定刚度和定阻尼的被动悬架系统; 类型5、6为变阻尼、定刚度的半主动悬架系统; 类型7、8为定阻尼、变刚度的半主动悬架系统; 类型9为变阻尼、变刚度的半主动悬架系统。

4 Matlab/Simulink仿真分析

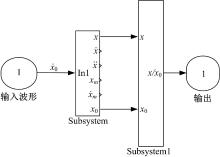
本文搭建的包含9种控制模式的Simulink模型如图6所示。其中Subsystem为采用开关阻尼控制算法的控制器模型。输出为簧载质量位移x、速度 $\overset{\cdot}{x}$ 和加速度 $\overset{\cdot \cdot}{x}$ 的时间历程, 以及弹簧阻尼元件串联点位移x_m、速度 ${\overset{\cdot}{x}}_{m}$ 以及地面位移x₀。由于分析悬架平顺性一般选取正弦路面激励和随机路面激励作为输入, 故本文也采用上述两种工况分析开关阻尼控制对该新型悬架平顺性的控制效果。

	Figure Option View Download New Window
	图6 Simulink仿真模型Fig.6 Simulink model

4.1 正弦路面激励下简化模型的响应

在正弦信号x₀=X₀sin(ω t)(其中, X₀=0.01 m)激励作用下, 各控制模式的簧载质量位移响应如图7所示。

由图7可见:①在相同的正弦激励下, 不同控制策略对应的系统簧载质量位移响应不同, 但它们都符合经典机械振动的一般规律, 振动幅值逐步衰减; ②除类型2(stiff)和类型1(soft)以外, 其他控制模式都使悬架系统具有比较好的减振性能。由此可见, 使用天棚控制方法可以达到需要的悬架减振性能, 有必要进行研究和推广。此外, 类型2(stiff)隔振效果最差, 振幅较高、振荡剧烈、衰减缓慢; 类型7(S on-off(low))隔振效果最好、平均振幅最小、振动微小。说明对于固定频率正弦激励输入, 通过实时调整悬架刚度值可以避免共振点, 在阻尼较小时可以明显减低振动幅值。对比还可发现, 正弦激励下类型4(high)与类型6(D on-off(stiff))具有非常接近的隔振效果, 都呈现较小阻尼隔振特征, 稍有超调, 但衰减很快; 类型3(low)与类型5(D on-off(soft))也具有非常接近的隔振效果, 都呈现较大阻尼隔振特征, 超调小, 衰减适中; 类型8(S on-off(high))与类型9(D+S on-off)也具有较为接近的隔振效果, 都呈现大阻尼隔振特征, 振动响应缓慢。

4.2 随机路面激励下简化模型的响应

以随机路面激励作为输入进行仿真评价。利用滤波白噪声生成法可以求得路面随机高程位移时域模型符合如下关系式^[13]:

$\overset{\cdot}{q} (t) + 2 π n_{0} Uq (t) = 2 π n_{0} \sqrt[]{G_{q} (n_{0}) U} W (t)$ （14）

式中:q $(t)$ 为路面随机高程位移函数; n₀=0.1 m^-1为参考空间频率; U=80 km/h为汽车行驶速度; W $(t)$ 为白噪声; G_q $(n_{0})$ 为参考空间频率n₀下的路面功率谱密度值, 称为路面不平度系数。

	Figure Option View Download New Window
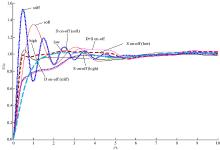	图7 正弦激励下簧载质量的位移响应Fig.7 Displacement response of suspended mass under sinusoidal input in time domain

运用3种典型路面进行仿真分析:①A级路面, S_q $(n_{0})$ =16× 10^-6 m³; ②B级路面, S_q $(n_{0})$ =64× 10^-6 m³; ③C级路面, S_q $(n_{0})$ =256× 10^-6 m³。

采用文献[14]方法, 经Matlab/Simulink计算仿真后得到的位移x和加速度 $\overset{\cdot \cdot}{x}$ 的均方根值如表2所示。悬架动挠度x-x₀、轮胎动载荷 $\overset{\cdot \cdot}{Mx}$ 的

均方根值仿真结果如表3所示。

由表2可见, 刚度和阻尼均为定值的被动控制模式的簧载质量位移明显大于变刚度或者变阻尼的半主动控制模式。在相同激励条件下, 9种控制模式中的D+S on-off控制模式对应的簧载质量位移是相对较小的, 其在C(rough)工况下的减振作用尤为明显; 对比可见, D+S on-off控制模式对应的簧载质量加速度比soft、S on-off(low)和stiff控制模式对应的簧载质量加速度大, 与D on-off(stiff)、D on-off(soft)控制模式对应的簧载质量加速度接近。

表2 随机激励下簧载质量位移和加速度均方根值 Table 2 Displacement RMS and acceleration RMS of suspended mass under random input

指代名称	阻尼器1	阻尼器2	A(smooth)		B(average)			C(rough)
指代名称	阻尼器1	阻尼器2		x/mm	$\overset{\cdot \cdot}{x}$ /(m· s^-2)	x/mm	$\overset{\cdot \cdot}{x}$ (m· s^-2)	x/mm	$\overset{\cdot \cdot}{x}$ /(m· s^-2)
Soft	off	off	2.1566	0.0517	4.3131	0.1033		8.6263	0.2066
Stiff	off	on	2.5243	0.0930	5.0485	0.1861		10.0971	0.3721
Low	on	off	1.8038	0.2421	3.6076	0.4843		7.2152	0.9686
High	on	on	1.9801	0.2425	3.9603	0.4851		7.9206	0.9701
D On-off (soft)	on-off	off	0.7178	0.1744	1.4355	0.3487		2.8710	0.6975
D On-off (stiff)	on-off	on	1.6092	0.1733	3.2183	0.3466		6.4367	0.6932
S On-off (low)	off	on-off	1.7396	0.0533	3.4793	0.1066		6.9585	0.2132
S On-off (high)	on	on-off	1.8168	0.2423	3.6336	0.4846		7.2672	0.9692
D+S On-off	on-off	on-off	0.6549	0.1768	1.3097	0.3535		2.6194	0.7071

表2 随机激励下簧载质量位移和加速度均方根值 Table 2 Displacement RMS and acceleration RMS of suspended mass under random input

表3 悬架动挠度、轮胎动载荷的均方根值 Table 3 Dynamic deflection RMS of suspension and dynamic load RMS of tire under random input

由表3可见, 9种控制模式在相同C(rough)工况激励条件下D+S on-off控制模式对应的悬架动挠度是最大的, 其轮胎动载荷也是处在最有利于整车操纵稳定性的范围内。同时刚度和阻尼均为定值的被动控制模式的减振表现、操纵稳定性明显劣于变刚度或者变阻尼的半主动控制模式, 并且D+S on-off控制系统在较差路面输入时减振表现、操纵稳定性比soft、S on-off(low)、stiff和D on-off(stiff)控制模式好, 且与D on-off(soft)控制模式对应的悬架动挠度和轮胎动载荷接近, 即它们在减振性及操纵稳定性方面表现近似。

5 结束语

研究了一种新型可变刚度和阻尼的半主动悬架系统, 主要针对具有9种刚度和阻尼开关控制模式的单自由度1/4整车模型进行了研究, 针对该悬架模型分别以正弦激励和随机白噪声激励作为模型输入, 通过仿真分析选取了部分悬架评价指标对9种控制模式仿真结果进行了对比分析。从结果可以看出, 可以同时改变刚度和阻尼的控制方法在较差路面输入条件下相对于其他的控制模式具有最优的输出, 表现出较好的性能, 具有理论研究价值; 参考汽车行驶的工况, 如能经过一定的信号处理电路的作用, 可以提出一种适用于全工况的控制系统, 其能在一定的路面输入条件下通过选择合适的控制策略实现整车良好的操纵稳定性和驾驶平顺性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	姚嘉伶, 蔡伟义, 陈宁. 汽车半主动悬架系统发展状况[J]. 汽车工程, 2006, 28(3): 276-280. Yao Jia-ling, Cai Wei-yi, Chen Ning. A review on the development status of automotive semi-active suspension systems[J]. Automotive Engineering, 2006, 28(3): 276-280. [本文引用:2]
[2]	王其东, 梅雪晴. 汽车半主动悬架的研究现状和发展趋势[J]. 合肥工业大学学报: 自然科学版, 2013, 36(11): 1289-1294. Wang Qi-dong, Mei Xue-qing. Research status and development tendency of vehicle semi-active suspension[J]. Journal of Hefei University of Technology(Natural Science), 2013, 36(11): 1289-1294. [本文引用:1]
[3]	Karnopp D, Crosby M J, Harwood R A. Vibration control using semi-active force generators[J]. Journal of Engineering for Industry, 1974, 96(2): 619-626. [本文引用:1]
[4]	Krasnicki E J. The experimental performance of an “on-off” active damper[J]. Shock and Vibration Bulletin, 1981, 51: 125-131. [本文引用:1]
[5]	Youn I, Semi-active suspension with adaptive capability[J]. Journal of Sound and Vibration, 1995, 180(3): 475-492. [本文引用:1]
[6]	Liu Y, Matsuhisa H, Utsuno H, et al. Controllable vibration of the car-body using magnetorheological fluid damper[J]. Vehicle System Dynamics Supplement, 2004, 41(4): 627-636. [本文引用:1]
[7]	Spelta C, Previdi F. Performance analysis of semi-active suspensions with control of variable damping and stiffness[J]. Vehicle System Dynamics, 2011, 49(1/2): 237-256. [本文引用:1]
[8]	Liu Y, MatsuhisaH, Utsuno H, et al. Vibration isolation by a variable stiffness and damping system[J]. International Journal of Japan Society of Mechanical Engineering, 2005, 48(2): 305-310. [本文引用:2]
[9]	范方强, 潘公宇. 变刚度和阻尼的半主动悬架的模糊控制研究[J]. 重庆交通大学学报: 自然科学版, 2012, 31(3): 482-485. Fan Fang-qiang, Pan Gong-yu. Fuzzy control of semi-active suspension with variable stiffness and damping[J]. Journal of Chongqing Jiaotong University(Natural Science), 2012, 31(3): 482-485. [本文引用:2]
[10]	靳立强, 刘阅. 基于汽车平顺性的新型半主动悬架研究[J]. 科学技术与工程, 2014, 14(29): 295-299. Jin Li-qiang, Liu Yue. Research on a new semi-active suspension for improving ride performance[J]. Science Technology and Engineering, 2014, 14(29): 295-299. [本文引用:1]
[11]	王军年, 叶涛, 孙文, 等. 一种可变刚度与阻尼的汽车馈能主动悬架系统[P]. 中国: CN104015582A, 2014 -09-03. [本文引用:1]
[12]	刘松山, 王庆年, 王伟华, 等. 惯性质量对馈能悬架阻尼特性和幅频特性的影响[J]. 吉林大学学报: 工学版, 2013, 43(3): 557-563. Liu Song-shan, Wang Qing-nian, Wang Wei-hua, et al. Influence of inertial mass on damping and amplitude-frequency characteristic of regenerative suspension[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 557-563. [本文引用:1]
[13]	陈杰平. 基于磁流变减振器的汽车半主动悬架设计与控制研究[D]. 合肥: 合肥工业大学汽车与交通工程学院, 2010. Chen Jie-ping. Research on design and control of automotive semi-active suspension based on magneto-rheological damper[D]. Hefei: School of Automotive and Transportation Engineering, Hefei University of Technology, 2010. [本文引用:1]
[14]	喻凡, 林逸. 汽车系统动力学[M]. 北京: 机械工业出版社, 2005. [本文引用:1]

2006

0.0

. 2006, 28(3):276-280

A review on the development status of automotive semi-active suspension systems

汽车半主动悬架系统发展状况

Yao Jia-ling , Cai Wei-yi , Chen Ning.

姚嘉伶, 蔡伟义, 陈宁

... 主动悬架包含一系列复杂的机械和电气化结构,通过额外注入作动力可以主动改变悬架的刚度和阻尼,自适应各种行驶路面,最大限度地改善整车行驶平顺性和操纵稳定性,但其能量消耗大、成本极高且结构复杂,同时主动悬架还使整车质量增加,因此现阶段主动悬架在汽车工业的运用还比较少^[1] ...

... 通过天棚控制方法实现调控阻尼较为简单,即合理选择参数就能够很好地抑制车身的垂直振动、俯仰和侧倾运动,提高车辆操纵稳定性和平顺性^[1] ...

2013

0.0

. 2013, 36(11):1289-1294 DOI:doi:10.3969/j.issn.1003-5060.2013.11.003

Research status and development tendency of vehicle semi-active suspension

汽车半主动悬架的研究现状和发展趋势

Wang Qi-dong , Mei Xue-qing.

王其东, 梅雪晴

文章简要介绍了汽车半主动悬架技术产生的背景,分析了半主动悬架的研究现状和最新研究成果,指出了半主动悬架研究的2个关键技术和影响半主动悬架快速发展的原因,阐述了不同类型的阻尼可调减振器的结构特点和工作原理,并将其结构和性能进行了对比;分析了应用于汽车半主动悬架系统的各种控制方法的优缺点及复合控制方法的优越性,最后探讨了半主动悬架研究的发展趋势。

... 半主动悬架一般用无源但参数有级或无级可调的被动元件(弹性元件或阻尼元件)替代执行机构的主动元件,能够改善乘坐舒适性和操纵稳定性^[2],其性能好于被动悬架,在控制品质上接近于主动悬架,且结构简单、无需作动源、能量损耗小,成本远低于主动悬架,因而是今后悬架系统的主要发展方向和值得推广的新兴技术 ...

1974

0.0

... 一些学者研究了一些基本的主动和半主动阻尼调节结构及其对应的控制算法^[3,4,5],例如用磁流变液减振器实现车身振动抑制^[6],此外,还研究了一些基本结构的刚度调节结构及其对应的控制策略^[7],但研究性能可靠、调节方便、既能实时变刚度又能变阻尼的半主动系统及与其对应的简单、有效的控制算法仍然很有必要^[8,9] ...

1981

0.0

1995

0.0

2004

0.0

2011

0.0

2005

0.0

... Liu等^[8]采用两组磁流变阻尼器与弹簧并联再串联的方式组成一种变刚度和阻尼的悬架模型,并以单自由度半主动系统为研究对象,建立了3种不同的开关阻尼控制策略,实现了刚度和阻尼的实时调节 ...

2012

0.0

. 2012, 31(3):482-485 DOI:doi:10.3969/j.issn.1674-0696.2012.03.29

Fuzzy control of semi-active suspension with variable stiffness and damping

变刚度和阻尼的半主动悬架的模糊控制研究

Fan Fang-qiang , Pan Gong-yu.

范方强, 潘公宇

为提高车辆的乘坐舒适性,建立了一种新型的四自由度的变刚度和阻尼半主动悬架模型.根据模糊控制理论,设计了两种适用于此模型的模糊控制器:常规模糊控制器和变论域模糊控制器.在MATLAB/SIMULINK仿真软件中建模,以积分白噪声随机路面输入作为激励,对被动悬架模型、常规模糊控制和变论域模糊控制的半主动悬架模型进行了仿真.仿真结果表明,与被动悬架相比,变刚度和阻尼半主动悬架能够有效降低车身垂直加速度和车身俯仰角加速度,有效地提高了车辆的乘坐舒适性.同时还表明,悬架的变论域模糊控制的减振效果优于常规模糊控制的.

... 国内学者也提出了一种可变刚度和阻尼的半主动悬架模型,并探讨了相应的模糊控制策略^[9]或PID控制策略^[10]的控制效果 ...

2014

0.0

. 2014, 14(29):295-299 DOI:doi:10.3969/j.issn.1671-1815.2014.29.057

Research on a new semi-active suspension for improving ride performance

基于汽车平顺性的新型半主动悬架研究

Jin Li-qiang , Liu Yue.

靳立强, 刘阅

摘　要：通过对车身加速度的频域分析,对车身加速度均方值相应进行了公式推导,提出了一种新型刚度和阻尼皆可变的半主动悬架;并且设计了其阻尼的控制算法.基于线性滤波法通过Simulink建立了路面输入模型,以四分之一车辆模型为基础通过AMESim和Simulink联合仿真平台在不同的路面上选取典型的速度区间对被动悬架、主动悬架以及提出的新式半主动悬架进行了模拟仿真比较.结果表明相比于主动悬架,在不良路面下,这种新型半主动悬架不仅减少了汽车的能量损耗;而且能够得到和主动悬架相近的性能.高速良好路面的时候,又能兼顾安全性,从整体上改善了汽车的平顺性.

... 国内学者也提出了一种可变刚度和阻尼的半主动悬架模型,并探讨了相应的模糊控制策略^[9]或PID控制策略^[10]的控制效果 ...

2014

0.0

... 如图2所示,直线电机4通过馈能电路F连接蓄电池G,馈能电路主要包括整流滤波电路和双向DC/DC变换器等原件,用于将由直线电机充当馈能减振器吸收的振动能量转化而成的电能进行整形变压后存储起来,再次循环利用,给磁流变阻尼器15提供电能^[11] ...

2013

0.0

. 2013, 43(3):557-563 DOI:doi:10.7964/jdxbgxb201303001

Influence of inertial mass on damping and amplitude-frequency characteristic of regenerative suspension

惯性质量对馈能悬架阻尼特性和幅频特性的影响

Liu Song-shan , Wang Qing-nian , Wang Wei-hua

刘松山, 王庆年, 王伟华

A complicated regenerative damper model containing regenerative motor and its control model was established to investigate the influence of inertial mass on damping characteristic. Analyzed by structural vibration method, the suspension natural frequency equation and the transfer characteristics of sprung/unsprung mass to road excitation were obtained. Alter the ratio of inertial mass to unsprung mass and analyze its influence on amplitude-frequency characteristic of body acceleration、suspension deflection and wheel dynamic load. The results show that the resonance frequency of regenerative suspension is prior to conventional suspension and the main weakness of inertial mass influence is that it increases the transfer characteristic of higher resonance frequency, although has little improvement for lower resonance frequency. With higher excitation frequency, it affects the ride comfort while has little influence on safety.

建立了包括馈能电机及其控制模型在内的馈能减振器Matlab/simulink仿真模型,分析了惯性力对馈能悬架阻尼特性的影响.利用结构振动分析方法,推导出馈能悬架固有频率的计算公式及对路面激励的传递特性.通过改变惯量比,分析了惯性质量对车身加速度、悬架动挠度和车轮相对动载荷的幅频特性的影响.结果表明:惯性质量使馈能悬架的共振频率较传统悬架提前;性能方面,低频共振区特性有一定的改善,而对高频共振区传递特性产生不利影响;更高激励频率对平顺性不利,而对安全性影响不大.

... 需要注意的是,由于可变阻尼器1采用的是直线电机,这种馈能减振器是通过滚珠丝杠将悬架的直线运动转化为电机的旋转运动,系统中旋转部件在悬架加、减速直线运动过程中,会由于惯量产生惯性力叠加到阻尼力f_d₁上^[12] ...

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1701030

Research on design and control of automotive semi-active suspension based on magneto-rheological damper[D]. Hefei: School of Automotive and Transportation Engineering,

基于磁流变减振器的汽车半主动悬架设计与控制研究[D]

Chen Jie-ping.

陈杰平

高速公路网的建设和延伸、点对点运输的实现、出行和运输效率要求的提高，促进了汽车工业的飞速发展。由于汽车行驶速度的提高，人们对汽车的行驶安全性、乘坐舒适性、操纵稳定性、道路友好性等提出了更高的要求。现代电子技术、信息技术、计算机技术和自动化技术的发展和在汽车上的应用，为改善汽车性能和满足人们对汽车性能的要求提供了手段，各类先进的技术在汽车上得到了应用，汽车正成为现代技术的试验场，集中体现着一个国家技术发展的水平。　　主动/半主动悬架是实现汽车底盘控制的重要部件之一，对改善汽车的行驶、操纵性能至关重要。以智能材料磁流...

... 利用滤波白噪声生成法可以求得路面随机高程位移时域模型符合如下关系式^[13]: ...

2005

0.0