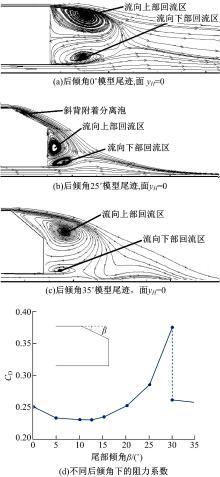
文献[2]根据实际车辆外形对气动性能的影响, 通过试验总结了不同尾部后倾角β 对应的三维定常流动及气动力系数, 如图1所示, 划分了3个阻力区域。由此提出的Ahmed body模型成为了整车气动设计和流动控制的标准模型。Ahmed body模型尾部各面间的棱边决定了气流皆从斜背和后垂直背的固定位置分离。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 不同后倾角下的尾迹和阻力系数CDFig.1 Wake and drag coefficient CDversus slant angle

(1)当0≤ β ≤ 12.5° , 如图1(a)(d)所示, 车顶气流在斜背完全附着, 在车顶和后垂直背交界处分离, 形成流向上部回流区。车底气流于后垂直背下端分离, 形成流向下部回流区。随着β 增大, 阻力系数C_D减小。

(2)当12.5≤ β ≤ 30° , 如图1(b)(d)所示, 车顶气流从斜背上端分离, 附着于斜背, 形成分离泡, 回流区外的气流继续向下游运动, 经后垂直背上端再次分离, 形成流向上部回流区。车底气流于后垂直背下端分离, 形成流向下部回流区。随着β 增大, C_D增大。

(3)当β ≥ 30° , 如图1(c)(d)所示, 车顶气流从斜背上端分离, 没有附着于斜背上, 直接形成流向上部回流区, 车底气流于后垂直背下端分离, 形成流向下部回流区。随着β 增大, C_D减小。

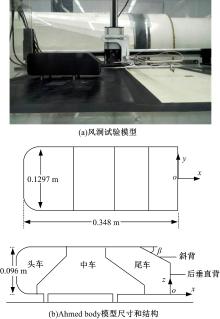
本文从以上3个区域中分别选取其中的模型作为研究对象, 即β =0° 、25° 和35° 模型, 分析其尾迹非定常流动的分布规律及其差异。采用1/3缩比的Ahmed body模型作为风洞试验模型, 如图2(a)所示, 模型长L=0.348 m, 宽W=0.1297 m, 高H=0.096 m; 简化轮胎为圆柱杆, 其直径为0.01 m, 离地间隙为0.0167 m。将Ahmed body模型设计为尾部可拆解结构, 如图2(b)所示, 尾车与中车通过螺栓连接, 更换不同后倾角的尾车即可进行试验。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 Ahmed body模型的试验布置Fig.2 Experimental arrangement of Ahmed body model

试验在上海地面交通工具风洞中心1/15整车缩比模型风洞进行。模型风洞为3/4开口式风洞, 最大风速为48 m/s, 喷口面积为0.123 m²; 试验段的湍流强度为0.38%^[3]。本次试验中的阻塞比为10%; 来流风速为30 m/s; 试验雷诺数Re为7× 10⁵。文献[10]认为, 不超过13%的阻塞比与不同雷诺数下的主频数、频率表征的非定常流动结构和空间分布规律等主要特征类似, 而频率值产生差异。

使用丹迪公司的Sreamlines热线风速仪对Ahmed body周围流场的瞬态速度进行测量。选取一维探头, 型号为55P01, 最多可提供4只探头同时测量。采样频率为10 000 Hz, 采样时间为40 s, 能反映足够高频率的连续瞬变信号。通过对移测架、支架和支杆及滑轨系统的控制, 实现对探头空间位置的精确控制。

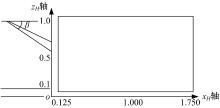
气流方向为x轴; 垂直地面方向为z轴; 车体展向为y轴。为了与以往风洞测量数据进行对比, 利用模型高度H分别对原三维坐标进行无量纲化, 得到新的坐标系:x_H=x/h, y_H=y/h, z_H=z/h, 坐标原点定义为后垂直背下端棱线的中轴位置在地面上的投影点o。在尾迹y_H分别为0、± 0.2、± 0.5、± 0.6、± 0.7等面内选择监测点, 进行速度测量。在y_H=0面上的测量范围如图3所示。测量点划分方法如下:从x_H=0.125起, 到x_H=1.75止, 每隔0.125进行测量; 从z_H=0.1起, 到z_H=1.0止, 每隔0.1进行测量; 面y_H=0上共测量154个点, 三维尾迹中监测点总数为1386。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 尾迹区测量范围, 面yH=0Fig.3 Measuring range in wake, in plane yH=0

非定常流动中的速度变量呈现为随机信号, 却又包含周期信号的特征。因此, 分别从频域和时域角度出发, 引入频谱和相关分析等方法, 加深对非定常流场的认识。

自功率谱密度(SPSD)描述了信号的能量分布, 信号的能量值为E_u, 利用频率f得到斯特劳哈尔数St_H=Hf U0-1。对于频率相等的空间两点, 将其信号进行互功率谱密度分析(CPSD)^[8], 得到两点间的相位差。其中, 相位差接近于π , 意味着两点相位反向。

相关分析是研究现象间是否存在某种依存关系并探讨其相关程度的时域方法^[11]。如表1所示, 利用互相关系数ρ _xy值的大小表征不同信号间的相关程度, ρ _xy定义如下:

ρxy=limT→∞1T∫0Tx(t)y(t+τ)dt/(σxσy)（1）

式中:σ _x、σ _y分别为信号x(t)和y(t+τ )的标准差。

表1

Table 1

表1(Table 1)

表1 相关程度 Table 1 Relationship correlation |ρ xy|=1.0 线性相关 0.95≤ |ρ xy|< 1.0 显著相关 0.8≤ |ρ xy|< 0.95 高度相关 0.5≤ |ρ xy|< 0.8 中度相关 0.3≤ |ρ xy|< 0.5 低度相关 0≤ |ρ xy|< 0.3 不相关

表1 相关程度 Table 1 Relationship correlation

如图4所示, 在面y_H=0内, 除了点G₁、H₁、I₁和I₂无峰值频率外, 其他各点皆含有峰值频率St_w=0.18。其中, 在点D₁、D₃、D₄、D₅、E₁、E₂和F₁的频谱中, 皆出现双频率峰值共存现象, 频率分别为St_s=0.13和St_w。文献[8]通过粒子图像测速法和模态分析(见图5)认为St_s和St_w分别对应了侧向回流区、流向上部及下部回流区的涡脱落作用。频谱中仅有单峰频率St_w的点, 沿着流向, 峰值先增大后减小, 说明该涡脱落作用的影响从增强到逐渐减弱。

图4

Fig.4

	Figure Option ViewDownloadNew Window
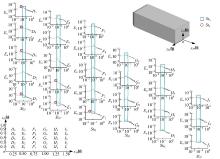	图4 后倾角0° 尾迹涡脱落频率分布, 面yH=0Fig.4 Vortex shedding frequency distribution in wake of rear slant angle 0° , in plane yH=0

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 后倾角0° 尾迹Fig.5 Wake of rear slant angle 0°

由于点F₂和F₄的频率相等, 给出两点相位差为0.8π , 说明两个流动结构相位接近反向, 呈现交替脱落模式。而点H₂与H₄的相位差为0, 说明在下游交替脱落消失。

图6

Fig.6

	Figure Option ViewDownloadNew Window
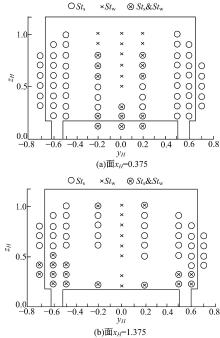	图6 后倾角0° 尾迹涡脱落频率分布, 面xH=0.375和xH=1.375Fig.6 Vortex shedding frequency distribution in wake of rear slant angle 0° , in plane xH=0.375 and xH=1.375

如图6(a)所示, 在面x_H=0.375内, 有2个频率, 分别为St_s和St_w。从y_H=± 0.7到y_H=0, 侧向回流区的涡脱落作用逐渐减弱, 而流向上部和下部回流区的涡脱落作用在中心区域较强。在两侧区域-0.7≤ y_H≤ -0.5和0.5≤ y_H≤ 0.7内, 含有峰值的监测点频率皆为St_s, 对于中心区域-0.2≤ y_H≤ 0.2, 含有峰值的监测点频率分别为St_s和St_w, 也出现了两个频率同时存在的现象。

面x_H=1.375在尾迹远场, 如图6(b)所示, 在其中心区域的监测点频率分布仍以St_w为主, 在两侧区域以St_s为主, 频率未关于y_H=0呈现完全对称分布。与面x_H=0.375的频率分布不同, 面x_H=1.375的两侧下部区域出现两个频率峰值同时存在的现象, 说明侧向回流区和流向上部及下部回流区的涡脱落作用对两侧下部区域皆有影响。

如图7所示, 在y_H=0面内, 除了z_H=0.9对应区域和点I₄无明显峰值外, 各点皆含有峰值频率St_w=0.38, 沿着流向, 峰值先升高再降低。文献[9]通过粒子图像测速法测量了不同时刻的流场, 认为St_w对应了流向上部和下部回流区涡脱落作用。点E₂、F₂和G₂同时出现了双峰值频率, 分别为St_d=0.76和St_w, 前者为后者的两倍, 这可能是由于流向上部和下部回流区中分别仅有较少一部分气流同时达到了相同水平的涡脱落作用, 在z_H=0.3处, 两股气流共同振荡, 导致了出现了St_d。由于点F₂和F₄的高峰值频率皆为St_w, 通过互功率谱密度分析给出相位差为0.9π , 说明两个非定常流动结构相位接近反向, 呈现交替涡脱落模式。而在更远的下游, 点H₂和H₄相位差为0, 交替涡脱落消失。

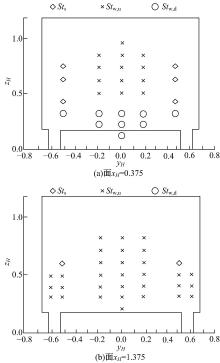
如图8(a)所示, 在面x_H=0.375内, 有3个频率, 分别为St_s、St_w和St_r。对于上部中心区域(0.5≤ z_H≤ 0.8, -0.2≤ y_H≤ 0.2)和下部区域(z_H< 0.5)内, 含有峰值的监测点频率皆包含St_w。说明流向上部及下部两个回流区的涡脱落作用影响中心区域流动, 也对两侧下部区域流动有影响。

在区域y_H=± 0.2且0.5≤ z_H≤ 0.8内的监测点, 出现频率St_r=0.17以及St_r和St_w共存的现象。如图7所示, 在斜背中心区域监测点S₁测得了St_r, 文献[6]通过粒子图像测速法试验的分析, 认为此频率对应了分离流在斜背的动态附着现象。通过互相关分析, 证明点S₁和尾迹中频率为St_r的点之间存在高度相关性, 说明斜背的动态附着作用对尾迹有影响。

图7

Fig.7

	Figure Option ViewDownloadNew Window
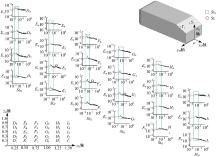	图7 后倾角25° 尾迹涡脱落频率分布, 面yH=0Fig.7 Vortex shedding frequency distribution in wake of rear slant angle 25° , in plane yH=0

图8

Fig.8

	Figure Option ViewDownloadNew Window
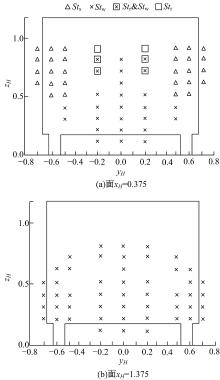	图8 后倾角25° 的尾迹涡脱落频率分布, 面xH=0.375 and xH=1.375Fig.8 Vortex shedding frequency distribution in wake of rear slant angle 25° , in plane xH=0.375 and xH=1.375

在两侧上部区域0.6≤ z_H≤ 0.9且-0.7≤ y_H≤ -0.5和0.5≤ y_H≤ 0.7, 各点峰值频率为St_s=0.23。如图7所示, 斜背侧边的监测点T₁处的频率也为St_s。通过互相关分析, 证明点T₁和尾迹中频率为St_s的点间均存在显著的相关性, 与尾迹中其他点不相关。如图7和图9所示, 点T₁处于C柱涡上游的形成区, 两侧上部区域处于C柱涡向下游延伸的尾迹内, 因此, St_s与C柱涡的流动有关。

对于两侧下部区域z_H< 0.5且y_H=± 0.6和± 0.7内的监测点, 均未测得峰值频率, 但在文献[9]中的对应位置监测到了两个峰值频率, 分别与车轮、底侧分离流的涡脱落作用有关。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 后倾角25° 涡量等值面Fig.9 Vortices isosuface contour of rear slant angle 25°

如图8(b)所示, 在面x_H=1.375内仅有St_w, 说明在远场的流动仅与流向上部和下部回流区的涡脱落作用有关。在面x_H=0.375和x_H=1.375, 频率皆关于y_H=0呈现对称分布。

如图10所示, 在y_H=0面上, 区域0.25≤ x_H≤ 0.75内的点D₁、D₂、E₁、E₂、F₁和F₂峰值频率均为St_{w, d}=0.1, 而E₃、E₄、E₅、F₃、F₄和F₅峰值频率均为St_{w, u}=0.21, 沿着流向峰值升高。文献[7]通过瞬态PIV试验, 认为St_{w, d}和St_{w, u}分别对应了流向上部和下部回流区的涡脱落作用。对于下游区域1.0≤ x_H≤ 1.5的监测点, 部分点已无峰值, 含有峰值的频率均为St_{w, u}, 沿着流向峰值降低, 说明此区域仅受流向上部回流区的涡脱落作用, 且影响逐渐减弱。

如图11(a)所示, 在x_H=0.375面内有3个频率St_s=0.16, St_{w, u}和St_{w, d}。在上部中心区域z_H≥ 0.5且-0.2≤ y_H≤ 0.2内, 含有峰值的监测点频率均为St_{w, u}, 说明上部中心区域的流动主要受流向上部回流区的涡脱落作用影响。而在下部区域z_H≤ 0.3内, 含有峰值的监测点频率均为St_{w, d}, 说明下部区域的流动主要受流向下部回流区的涡脱落作用影响。对于区域y_H=0.6和y_H=0.7上的监测点, 没有捕捉到峰值频率。

对于两侧上部区域y_H=0.5且0.4≤ z_H≤ 0.7的监测点, 含有峰值的频率均为St_s。斜背侧边的点T₂处频率为St_s。通过互相关分析证明点T₂与尾迹中频率为St_s的点之间存在显著相关性。如图10和图12所示, 点T₂处于C柱涡形成的区域, 两侧上部区域处于C柱涡延伸至下游的尾迹内, 因此, St_s与C柱涡的流动有关。

如图11(b)所示, 在x_H=1.375面内, 坐标为y_H=± 0.5且z_H=0.6的点对应频率为St_s, 说明此处仍受C柱涡影响。而此面内其余各点仅存在频率St_{w, u}。说明远场主要受上部回流区的流向涡脱落作用影响。对于面x_H=0.375和x_H=1.375, 所测量结果呈对称分布。

图10

Fig.10

	Figure Option ViewDownloadNew Window
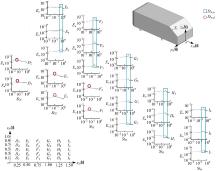	图10 后倾角35° 尾迹涡脱落频率分布, 面yH=0Fig.10 Vortex shedding frequency distribution in wake of rear slant angle 35° , in plane yH=0

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 后倾角35° 的尾迹涡脱落频率分布Fig.11 Vortex shedding frequency distribution in wake of rear slant angle 35°

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 后倾角35° 涡量等值面Fig.12 Vortices isosuface contour of rear slant angle 35°

模型尾部后倾角的不同使得尾迹结构和涡脱落模式存在差异, 进而导致频率分布的不同。其中, 0° , 25° 和35° 后倾角模型的尾迹内, 分别含有2个、4个和3个主要的涡脱落频率。在不同的展向截面上, 25° 和35° 后倾角模型的尾迹涡脱落频率皆关于中心对称面呈对称分布, 0° 后倾角模型的涡脱落频率在大多数位置关于中心对称面呈对称分布。

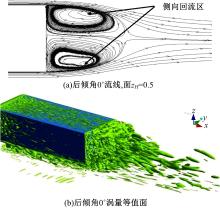
后倾角0° 模型没有斜背(或可认为流动完全附着于斜背), 未产生C柱涡, 尾迹中仅测量到2个涡脱落频率St_w和St_s, 分别对应流向回流区、以及侧向回流区的涡脱落作用, 且在一些位置上出现了双频率峰值共存的现象。

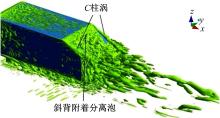
气流从后倾角25° 模型的车顶与斜背交界处分离, 一部分气流在斜背两侧区域, 与侧向气流掺混, 形成C柱涡, St_r对应了C柱涡的作用。同时, 另一部分在中心对称面区域的气流附着于斜背, 如图9所示, 形成斜背附着分离泡, 其不断的拍打着斜背, 附着点沿壁面移动的动态附着作用影响了尾迹流动, 因此, St_s对应了分离流在斜背的动态附着作用。回流区外的附着流继续向下游运动, 在后垂直背分离形成上部回流区, 与车底气流分离形成的下部回流区共同构成了尾迹区。在近场尾迹, 上下回流区内的两股非定常流动结构间存在交替脱落, 且两股流动结构间产生共振作用, 出现频率St_b=2St_w, 在远场共振现象消失, 仅存在频率St_w, 交替涡脱落消失。

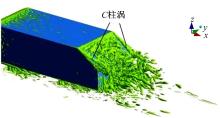
随着后倾角的增大, 35° 后倾角模型的C柱涡破裂^[5], St_s对应C柱涡的作用。同时, 中心区域的气流从车顶后缘直接分离, 形成流向上部回流区, 如图9所示, 未在斜背附着, 与车底气流分离形成的流向下部回流区共同构成了尾迹区。流向上部和下部回流区的涡脱落作用分别对应频率St_{w, d}和St_{w, u}。

对于0° 和25° 后倾角模型, 分离位置皆位于后垂直背上下两端, 但0° 后倾角模型的后垂直背高于25° 后倾角模型的, 因此上端分离位置产生差异, 导致了流向的尾迹和涡脱落模式的不同。而35° 后倾角上端分离位置位于斜背上端, 使得尾迹中上部回流区的形成位置在x_H轴的坐标与0° 和25° 模型不同, 导致35° 模型的流向上部和下部回流区的对应了两个不同的频率。