作者简介:李明达(1982-),男,讲师,博士研究生.研究方向:车路协同节能技术.E-mail:limingda_123@qq.com
针对具有复杂底部结构的五轴重型载货汽车气动阻力进行研究,建立了与实车外形结构一致的车辆模型,利用基于格子玻尔兹曼方法的计算流体动力学软件XFlow,模拟了模型外流场流体的宏观行为。进行了模型的格子尺度优化试验,得到整车模型的空气阻力系数以及底部结构对整车气动阻力的影响。对模型底部压力分布、旋转车轮的表面速度分布、模型底部外流场速度分布、湍流强度分布以及车辆模型底部粒子轨迹线进行了分析,根据分析结果对车辆模型底部进行结构优化。仿真结果表明:车辆模型的空气阻力系数误差在6%以内,对模型底部结构进行优化可以降低整车空气阻力系数23%。
The aerodynamic drag of five axes heavy duty vehicle with complex underbody structure was studied. The model with the real vehicle structure shape was established. Then, the macroscopic behavior of fluids in external flow field was simulated using the computational fluid dynamics software XFlow, which is based on Lattice Boltzmann Method. The air resistance coefficient of the whole vehicle model was obtained by lattice scale optimization test, and the influence of the underbody structure on the aerodynamic drag was investigated. The vehicle surface pressure distribution, the surface velocity field of the rotating wheels, the velocity distribution in the external flow field of the model, the turbulence intensity distribution, and the particle trajectories under the vehicle were analyzed. Results show that the drag coefficient error of the truck model is within 6%. Through the underbody structure optimization, the aerodynamic drag coefficient of the whole vehicle model can be reduced by 23%.
空气动力学分析是汽车节能研究的重要手段。目前, 国内外针对车辆底部的空气动力学的研究多针对轿车, 例如:谷正气[1]、王靖宇[2]、杨志刚[3]等分别研究了车轮辐板形状、轿车底部外形以及车轮宽度对汽车气动阻力的影响; Mcmanus[4]、傅立敏[5, 6]、胡兴军[7]等将车轮独立出来进行气动阻力分析; Angelo[8]、Regert[9]等进行了1/2或1/4汽车模型的空气动力学研究。而针对重型卡车的空气动力学研究中, 由于受到车辆三维模型复杂程度的限制, 其底部结构多做简化处理, 例如:Nakashima等[10]研究的三轴重型载货汽车模型底部仅有车轮, 无车轮罩; EI-Alti等[11]使用的1∶ 10比例的Volvo卡车模型具有详细的驾驶室结构但简化了底部结构和车轮罩; Mattana等[12]研究的五轴重型载货汽车模型也无车轮罩, 导流板为简化结构, 将挂车简化为长方体等。以上研究对车辆底部结构的复杂性和非对称性考虑不足, 与实际工况下的车辆外流场有一定差异。
针对以上问题, 本文建立了外形结构与实车一致的五轴重型载货汽车模型。通过基于格子玻尔兹曼方法的流体动力学软件进行了复杂底部结构下的空气动力学分析, 研究了底部结构对整车模型的空气动力学影响。
传统的计算流体动力学(Computational fluid dynamics, CFD)方法是基于有限差分或有限体积法进行空间离散的近似。在进行汽车空气动力学分析时, 需进行大量的网格划分工作, 并在模型局部进行网格细化以达到仿真实验的精度, 因此开发周期较长, 且汽车模型多为简化模型。而XFlow与传统的流体动力学软件相比具有以下优势:
(1)采用基于粒子的动力学求解器求解格子玻尔兹曼方程, 通过介观模型的动力学方法来模拟流体的宏观行为, 因此兼顾了宏观流体动力学的高效和微观分子动力学的精度。
(2)在模拟仿真中, 自动地对计算空间进行格子形式离散化, 因此在前处理阶段模拟空间不需要划分网格, 极大地提高了仿真效率。
(3)在湍流模型上, 将精确的大涡模拟与格子玻尔兹曼方法结合, 增强了对复杂几何模型和移动边界问题的处理能力, 模型无需简化, 可实现实车模型的空气动力学分析。
(4)具有粒子自适应性, 仿真过程中可以动态地跟踪汽车尾部流场粒子的运动轨迹, 进行粒子的局部细化, 提高了近场壁面和尾流处的仿真精度。
表1为车辆的基本参数, 从表中可以看出整车尺寸较大, 受格子尺度的影响, 如果直接对该车辆进行仿真, 其计算量将非常巨大, 因此考虑将车辆模型进行适当缩放。
| 表1 五轴重型载货汽车模型参数 Table 1 Five axis heavy duty vehicle model parameters |
表1中:Hvel为整车高度; Wvel为整车宽度; Lvel为整车长度; Aref为该模型的迎风面积; δ t_t为牵引车与挂车之间间距; rw为车轮半径; Ltra为牵引车长度; Re为有效车轮半径; δ w_t为轮距。
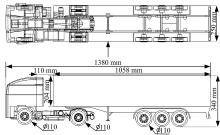
模型采用缩放比为1∶ 10。图1为缩放模型的基本尺寸示意图, 可以看出, 模型完整地反映了整车底部结构的复杂性和非对称性。
(1)虚拟风洞
虚拟风洞的基本参数如表2所示。表2中, Hvwt、Wvwt和Lvwt分别为虚拟风洞的高度、宽度和长度; vin为来流速度, 即虚拟风洞入口处流体速度; ρ 为空气密度; T为风洞内温度; xL为车辆模型与虚拟风洞入口的距离; μ 为流体的动力黏度; vg为地面移动速度。
| 表2 虚拟风洞基本参数 Table 2 Basic parameters of virtual wind tunnel |
(2)壁面模型函数
由于车辆模型较为复杂, 需要考虑多种干扰和相互影响, 因此使用模拟壁面梯度变化的非平衡壁面函数代替实际边界的流动, 该函数考虑了壁面的压力梯度, 因此适合用于流体分离比较严重的区域。
(3)尾流控制距离
由于XFlow软件带有粒子自适应技术, 该技术会导致尾流处格子数越来越多, 增加不必要的计算量, 因此需设置尾流控制距离, 该参数可以保证格子加密控制在一定的距离范围内, 其值设置为缩放模型车身长度的3.5倍。
车辆外流场边界层的格子尺度直接影响车辆空气阻力系数的计算精度与准确性, 然而格子尺度并不是越小越好, 过小的格子不仅会消耗大量的计算资源, 而且由于几何模型复杂程度的差异, 计算精度也不一定准确, 因此需通过试验寻找最优的格子尺度。
(1)确定模型加密区域
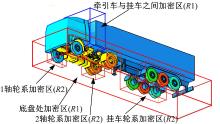
重型载货汽车与乘用车相比具有相对复杂的几何结构, 而在模拟仿真中, 微小的几何变化也会对结果产生很大的影响, 因此需要将车辆结构复杂区域进行局部格子加密, 模型中牵引车与挂车之间间隙、车辆模型底部、车轮与车轮罩之间以及车轮附近的流场运动相对复杂, 因此在模型中添加加密区如图2所示。
从图2中可以看出, 各轮系加密区是在底盘处加密区内的, 因此将图中牵引车与挂车之间加密区、底盘处加密区定义为R1; 各轮系加密区命名为R2。
(2)格子尺度优化
按照表3设置仿真参数进行格子尺度优化试验, 表中初场粒子数按照序号顺序呈递增趋势。
| 表3 格子尺度的仿真参数 Table 3 Simulation set of lattice scale |
表3中, xfar为远场壁面粒子之间间距; Knr、KR1、KR2以及Kw分别为近场壁面、加密区R1、加密区R2以及尾流格子尺度与xfar的比值; ni为初场粒子数量。
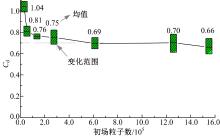
根据表3参数进行仿真得到的车辆的空气阻力系数Cd值变化情况如图3所示。图3中横坐标为初场粒子数, 粒子数越多则计算量越大; 纵坐标Cd为仿真0.1 s后的均值, 柱状体为Cd值在收敛过程中的变化范围。
从图3中可以看出:粒子数超过6.0× 105时, Cd值趋于稳定, 最后3次试验的阻力系数均值分别为0.69、0.70、0.66, 最小格子尺度已达到2.9 mm, 足够模拟底部流场流动情况, 因此整车模型的空气阻力系数取3次模拟仿真的均值0.683, 该值与美国能源部进行的1∶ 1整车风洞实验结果相差5.2%[13]。因此确定第7次仿真试验参数为最优格子尺度, 后文均为此尺度下的仿真实验结果。
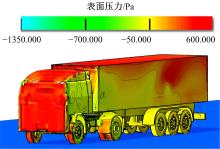
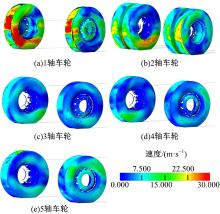
图4为车辆表面压力分布情况, 可以看出, 在车辆底部结构中1轴车轮和2轴车轮表面压力较大, 而挂车车轮的表面压力很小。
图5为车轮旋转时各轴车轮的外表面速度场分布情况, 可以看出:1轴2车轮上半部与内侧表面速度较大; 2轴4车轮表面速度相对减小; 3、4、5轴各车轮表面速度场速度较低, 与压力分布情况相符, 因此挂车车轮对气动阻力影响较小。
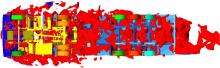
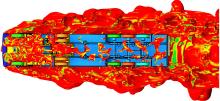
图6为车辆底部外流场速度分布情况。红色部分为车辆外流场流体速度为10 m/s的区域, 可以看出, 红色区域遍布于车辆底部, 说明模型底部流体速度较低。图7为模型底部的湍流强度分布情况, 可以看出:由于车辆模型底部结构较为复杂, 造成了气流的阻塞, 但是湍流损失较大, 因此挂车底部对于整车的空气阻力影响不应忽视。
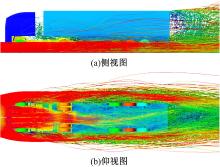
图8为车轮旋转状态下, 模型前方车高1/4处1.0× 103个粒子经过车辆底部的运动轨迹, 从图8(a)可以看出, 粒子受模型底部影响已在牵引车与挂车之间、尾流处形成大量涡流; 从图8(b)可以看出模型底部的不对称性导致的粒子流向变化。因此, 底部结构对于牵引车与挂车之间和尾流处的流场影响较大。
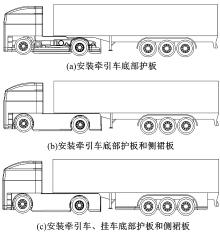
根据车辆模型底部流场的分析结果对模型进行结构优化(见图9), 分别在模型底部安装底部护板和侧裙板。
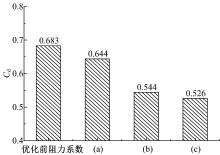
优化结果如图10所示, 横坐标中(a)、(b)、(c)分别代表图9中的3种底部结构优化方式, 可以看出, 牵引车底部对整车空气阻力的影响较大, 将牵引车底部封闭后, 整车阻力系数降低了20.4%; 将牵引车和挂车底部进行封闭后, 整车阻力系数降低了23%。
(1)建立与实车外形结构一致的重型载货汽车模型, 在基于格子玻尔兹曼方法的流体动力学软件中进行了空气动力学分析。
(2)通过格子尺度优化试验确定了车辆模型的空气阻力系数, 与美国能源部的实车风洞实验结果比, 误差不超过6%, 具有一定的精度。
(3)对车辆模型底部的流场进行了分析, 并对底部结构进行了优化, 使整车空气阻力系数降低了23%。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|