作者简介:李显生(1965-),男,教授,博士生导师.研究方向:车辆行驶可靠性与安全技术.E-mail:lixs@jlu.edu.cn
为了解汽车罐车的行驶稳定性、探索有效的行驶稳定性控制策略,对圆形和椭圆形横截面罐体内的液体冲击进行了仿真模拟,并借助时域和频域分析了非满载罐体内液体冲击的动力学特性。结果表明:液体冲击在时域内呈周期性;其奇数阶振荡模态是非对称波,会使液体质心发生位移,而偶数阶振荡模态是对称波,不会使液体质心发生位移。而且,一阶共振频率是液体冲击的主导频率。充液比和外界激励是影响液体冲击动力学特性的主要因素。当充液比一定时,外界激励的增加使液体冲击的非线性增强、冲击力增大;当外界激励一定时,充液比的增大也会使液体冲击的非线性增强。
In order to understand the handling stability of tanker and explore effective stability control strategy, the liquid sloshing in partially-filled tanks with circular or elliptical cross-section is simulated using FLUENT, and the corresponding parameters are recorded. Then, the recorded data are processed in time and frequency domains. It is discovered that liquid sloshing presents periodic characteristics. The odd oscillation modes have asymmetrical waves, which contribute to the moving of the gravity center of liquid. Besides, the first oscillation mode contributes most to the moving of the gravity center. At the same time, the even oscillation modes have symmetrical waves, which do not contribute to the moving of the gravity center of liquid. It is also found that the filling percentage of liquid and external excitation are the main factors. The growth of the external excitation increases the nonlinear feature of liquid sloshing. Also, the growth of the liquid filling level also increases the nonlinear characteristics of liquid sloshing.
侧翻是罐车主要的事故类型[1]。进一步的研究发现, 非满载罐体内的液体冲击是造成罐车侧翻的主要原因之一。为了解汽车罐车的行驶稳定性并探索有效的行驶稳定性控制策略, 首先需要探究罐体内液体冲击的动力学特性。
罐体内液体冲击的研究方法主要有准静态方法(Qusia-static, QS)[2, 3]、流体动力学法[4]、等效机械模型法[5, 6, 7]、试验和仿真方法[8]。准静态法利用流体静力学理论描述液体冲击作用。该方法假定侧向激励下液体自由表面是倾斜平面, 并推导了平面倾斜率关于侧向激励的函数。据此, 求解每一时刻的液体质心位置并估计液体冲击力。流体动力学法利用流体动力学理论描述非满载罐体内的液体冲击, 通过建立动量、质量及能量守恒方程等求解液体冲击力和力矩, 是研究罐体内液体冲击动力学特性的最基本方法。等效机械模型法将液体冲击流体动力学问题转换成机械运动问题, 利用机械模型近似描述非满载罐体内的液体冲击, 大大简化了流固耦合问题的求解。试验法通过实际罐体或者比例缩小罐体内的冲击试验对液体冲击特性进行研究, 它作为其他方法的一种验证手段, 贯穿了整个研究历程。仿真法是利用流体运动分析软件模拟流体的流动和发展过程, 并通过后处理器对所得结果进行显示, 目前已广泛应用于罐体内液体冲击动力学特性的研究。
本文研究了汽车罐车非满载罐体内的液体冲击特性及其影响因素, 并进一步探究了液体冲击的作用机理。通过建立汽车罐车罐内液体冲击仿真模型, 利用FLUENT和ANSYS对汽车罐车罐内液体的冲击行为进行仿真分析, 通过对仿真数据的分析和处理获得液体冲击动力学特征, 揭示了液体冲击的实质。
汽车罐车罐内液体的冲击受多种因素的影响, 主要影响因素包括罐体的形状和尺寸、罐体充装率、作用在罐体上的侧向激励等。
(1)罐体形状和尺寸
罐体横截面形状多分为圆形和椭圆形, 如图1所示。罐体的横截面面积多为2.5 m2左右。
在实际生产中, 椭圆形横截面的长短轴之比大多小于2。因此, 令椭圆形横截面的长短轴之比为1.0~2.0, 变化步长为0.2。当椭圆形横截面的长短轴之比为1时, 此时椭圆即为圆。将不同尺寸的罐体编号为C0~C5。由此, 得到罐体的横截面尺寸, 如表1所示。表1中, a为罐体横截面宽度的1/2; b为罐体横截面高度的1/2。
| 表1 罐体的横截面尺寸 Table 1 Cross-sectional dimensions of the tank |
(2)罐体充装率
为了保障货物运输安全, 罐体充装率一般不超过90%。充装率定义为罐内液体体积与罐体体积之比, 即:
式中:δ 为罐内液体的充装率; S1为液体横截面面积; S2为罐体横截面面积。
为了探究不同充装率条件下的液体冲击特性, 令充装率由0.4变化至0.9, 变化步长为0.1。为描述简单起见, 进一步将充装率转化为液面高度, 并利用充液比描述液面高度与罐体高度的比值, 即:
式中:Δ 为充液比; h为自由液面距离罐体底部的距离; 2b为罐体高度。
对于圆形和椭圆形横截面罐体而言, 其充装率与充液比的关系可表示为:
经计算可知, 当圆形和椭圆形横截面罐体内的液体充装率为0.4~0.9时, 其充液比也近似为0.4~0.9。
(3)作用于罐体上的侧向激励
罐车在行驶过程中, 车身上常作用有侧向力, 为保持车辆运行稳态, 作用于车身上的侧向加速度一般小于0.4g。因此, 本文设定作用于罐体上的侧向加速度为0.1g~0.4g。
利用FLUENT软件对非满载罐体内的液体冲击进行仿真模拟。首先在二维平面坐标系中构建有限元模型, 坐标系原点位于罐体中心处。边界条件为罐体壁面, 罐体内部全部为流体域, 并采用四面体单元对流体域进行网格划分, 单元尺寸选择0.01 m。进行液体冲击仿真时, 选择空气和水作为罐体内的气相和液相。液体冲击的有限元模型如图2所示。
罐体上未作用有纵向力时, 不同横截面上的侧向液体冲击近似相同。据此, 将实际的三维液体冲击简化为二维冲击, 用任意横截面上的侧向冲击表示非满载罐体内的侧向液体冲击情况, 并据此建立非满载罐体内的液体冲击二维仿真模型, 如图3所示。
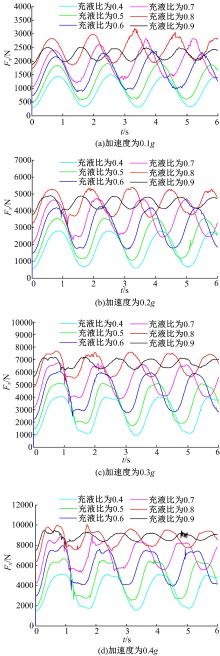
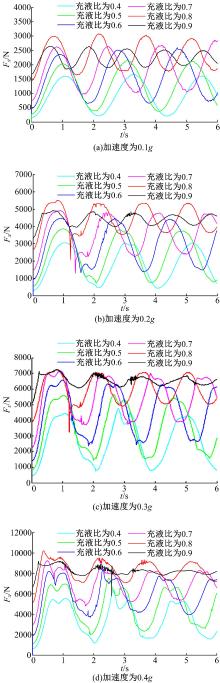
受篇幅的限制, 本文只给出C0和C3罐体的仿真结果, 分别如图4和图5所示。令充液比由0.4变化至0.9, 变化步长为0.1; 施加在罐体上的侧向加速度由0.1g变化至0.4g, 变化步长为0.1g。
由图4可知, 罐内液体的冲击力呈现周期性变化, 充液比为0.8左右时, 罐内液体的侧向冲击力最大。侧向激励一定时, 随着充液比的增大, 侧向冲击力呈增大趋势, 非线性增强; 当充液比一定时, 随着侧向激励的增大, 罐内液体冲击的非线性增强, 周期性下降。
由图5可知, C3和C0罐体内液体的冲击力具有近似相同的特性。
对全部罐体内液体冲击的时变曲线进行分析, 可得到如下结论:罐内液体的冲击力具有周期性。当充液比一定时, 随着侧向激励的增大, 罐内液体的冲击力增大, 液体冲击的非线性增强, 周期性下降。当侧向激励一定, 充液比为0.7~0.8时, 罐内液体的侧向冲击力最大。
液体冲击力的时域信号不能反映出信号的频域结构, 比如主导信号的频率、幅值等。时域的信号可以通过傅里叶变换转换成频域的信号, 并利用模态分析方法获得各个频率的模态振型。
罐体内液体冲击的频域参数仿真结果如表2~表9所示。受篇幅的限制, 本文仅给出C0罐体和C3罐体的仿真结果。
| 表2 C0罐体侧向加速度为0.1g Table 2 Lateral acceleration is 0.1g in C0 |
| 表3 C0罐体侧向加速度为0.2g Table 3 Lateral acceleration is 0.2g in C0 |
| 表4 C0罐体侧向加速度为0.3g Table 4 Lateral acceleration is 0.3g in C0 |
| 表5 C0罐体侧向加速度为0.4g Table 5 Lateral acceleration is 0.4g in C0 |
| 表6 C3罐体侧向加速度为0.1g Table 6 Lateral acceleration is 0.1g in C3 |
| 表7 C3罐体侧向加速度为0.2g Table 7 Lateral acceleration is 0.2g in C3 |
(1)C0罐体内液体冲击的频域参数
侧向激励分别为0.1g、0.2g、0.3g、0.4g时, 液体冲击的频域参数分别如表2~表5所示。
由表2~表5可知, 任意充液比条件下, 罐内液体冲击都存在二阶及以上冲击频率, 且一阶冲击频率的幅值远大于二阶冲击频率的幅值。当罐体受到外界冲击频率与罐内液体冲击的一阶冲击频率相近时, 会与罐体内液体晃动发生共振, 使液体对罐壁的冲击强度达到最大。
(2)C3罐体内液体冲击的频域参数
侧向激励分别为0.1g、0.2g、0.3g、0.4g时, 冲击频域参数分别如表6~表9所示。
| 表8 C3罐体侧向加速度为0.3g Table 8 Lateral acceleration is 0.3g in C3 |
| 表9 C3罐体侧向加速度为0.4g Table 9 Lateral acceleration is 0.4g in C3 |
由表6~表9可知, C3和C0罐体内的液体冲击具有相同的频率特性。
对全部罐体内的液体冲击频域参数进行分析, 可以得到如下结论:罐内液体的一阶冲击频率是液体晃动的主导频率, 并且罐内液体不论是线性冲击还是非线性冲击, 都可以通过一阶冲击频率及其对应的幅值来反映液体的晃动特征。
模态分析具有确定物质结构振动特性的能力, 通过模态分析可以获取一个结构的固有频率、模态振型等。
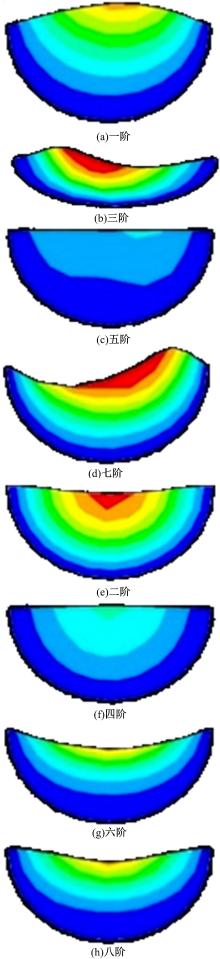
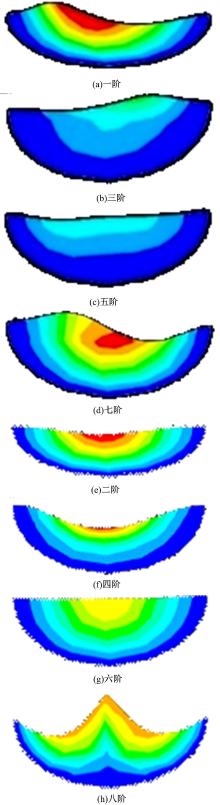
液体冲击的模态振型如图6和图7所示。受篇幅的限制, 本文仅给出了C0罐体和C3罐体内液体冲击的模态振型仿真结果。
由图6可知, C0罐体内液体冲击的奇数阶模态振型是非对称波, 偶数阶模态振型是对称波。
由图7可知, C3和C0罐体内液体冲击的奇数阶模态振型具有相同的振动特性, 偶数阶模态振型也具有相同的振动特性。
对全部罐体内的液体冲击进行模态分析, 可以得到如下结论:罐内液体冲击的奇数阶模态振型是非对称波, 会引起液体质心的移动, 偶数阶模态振型是对称波, 不会引起液体质心的移动。
(1)充液比和外界激励是影响液体冲击特性的关键因素。当充液比一定时, 随着外界激励的增大, 液体冲击的非线性增强, 冲击力增大; 而当外界激励一定时, 随着充液比的增大, 液体冲击的非线性也会增强。为了有效抑制液体冲击, 可在罐体内安装角度合适的防波板, 以此提高罐车行驶稳定性。
(2)液体冲击呈现周期性变化。其奇数阶模态振型是非对称波, 会使液体质心产生位移; 其偶数阶模态振型是对称波, 不会使液体质心产生位移。不仅如此, 一阶振动频率是液体晃动的主导频率, 最能代表液体冲击的动态特性。
(3)为保障车辆运输安全, 应使车辆固有振动频率远离一阶液体冲击频率。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|