引用本文
曲昭伟, 曹宁博, 陈永恒, 白乔文, 赵利英, 罗瑞琪. 考虑违章行人的行人过街位置分布模型. 吉林大学学报(工学版), 2017, 47(3): 744-750
QU Zhao-wei, CAO Ning-bo, CHEN Yong-heng, BAI Qiao-wen, ZHAO Li-ying, LUO Rui-qi. Modeling of pedestrians' crossing position distribution considering violating pedestrians. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 744-750  
Doi:10.13229/j.cnki.jdxbgxb201703008
Permissions
Copyright©2017, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
考虑违章行人的行人过街位置分布模型
曲昭伟, 曹宁博, 陈永恒, 白乔文, 赵利英, 罗瑞琪
吉林大学 交通学院,长春 130022
陈永恒(1978-),男,副教授,博士.研究方向:交通控制与交通组织.E-mail:cyh@jlu.edu.cn

作者简介:曲昭伟(1962-),男,教授,博士生导师.研究方向:交通流理论,交通视频处理,交通控制.E-mail:quzw@jlu.edu.cn

基金项目:国家自然科学基金项目(51278220; 51278520)
摘要

利用视频处理技术对过街行人的全时空信息进行采集,分析了违章行人与转弯车辆冲突的内在规律,并提出了行人过街位置分布的建模方法。首先,利用调查数据定性分析了行人过街位置对人车冲突的影响。其次,通过对多交叉口不同时刻行人(包括违章行人)行走位置的统计分析,得到绿灯消散时间和人行横道长度对行人过街位置的影响。结合调查数据,利用Gauss函数对不同时刻的行人过街位置分布进行建模,建立绿灯消散时间和人行横道长度与Gauss函数模型参数的关系等式,拟合模型的 R2分别达到0.9、0.93、0.97,表明模型能够很好地反映行人过街位置分布规律。最后,对模型进行了验证,在所建立模型的基础上,分析了行人过街位置分布规律对行人与转弯车辆冲突区域判别的作用,并提出减小冲突区域的优化方法。

关键词: 交通运输系统工程; 信号交叉口; 违章行人; 转弯车辆; 冲突区域
中图分类号:U491 文献标志码:A 文章编号:1671-5497(2017)03-0744-07
Modeling of pedestrians' crossing position distribution considering violating pedestrians
QU Zhao-wei, CAO Ning-bo, CHEN Yong-heng, BAI Qiao-wen, ZHAO Li-ying, LUO Rui-qi
College of Transportation, Jilin University, Changchun 130022, China
Abstract

Video-processing technology was used to acquire detailed spatio-temporal data of pedestrians, and the underlying law of the conflict between violating pedestrians and turning vehicles was analyzed, then a model of pedestrians' crossing position distribution was proposed. First, on the basis of the survey data, the relationship between conflict and pedestrian crossing distribution was qualitatively analyzed. Then, based on the analysis of pedestrians' crossing positions at seven surveyed crosswalks, the impacts of crosswalk length and elapsed time on pedestrians' crossing position distribution were investigated. Further, a Gauss function was applied to model the pedestrians' crossing position distribution at different times. Finally, the formulas about elapsed time, crosswalk length and three model parameters were established. The adjusted R2 of the fitting models were 0.9, 0.93 and 0.97 respectively, which indicates that the proposed models can well represent the law of pedestrians' crossing position distribution. The proposed model was verified and the role of the model on determining the conflict zone was illustrated. An optimization method to reduce the conflict zone was put forward.

Key words: engineering of communications and transportation system; signalized intersection; violation pedestrians; turning vehicles; conflict zone
0 引言

人行横道设计的目的是保证行人过街安全并减少行人和机动车之间的冲突。然而, 无论是在时间上(信号灯)还是空间上(人行横道线), 行人并不总是遵守过街规则。目前, 提高行人在信号交叉口的过街安全依旧是一个严峻的问题。因为在很多信号交叉口, 转弯车辆通常和行人同时释放, 虽然理论上转弯车辆需要避让行人, 但是因为交通环境、行人运动方向和交叉口的几何布局等因素的影响, 转弯车辆通常会冒险选择较小的行人间隙通过而不是让行, 这直接威胁到行人安全。定量分析绿灯消散时间和人行横道长度对行人和转弯车辆冲突区域的影响能够为行人过街安全评估和完善现有行人过街安全措施提供依据。

目前关于该方面的研究集中在行人与转弯车辆的冲突判别和冲突严重性的判断。Chen等[1]指出较高的转弯速度和高频率的后侵占时间(PET)容易导致较高的冲突率。Perkins等[2]首先提出了交通冲突技术, 通过冲突频率和严重程度来评估行人安全性, 冲突频率和冲突严重性可以通过PET和冲突时间[3, 4]来反映。Tang等[5]也利用PET来表示冲突的严重性, 指出PET值越小表示冲突越严重。然而其他研究却并不支持这个结论, 他们认为PET无法将车辆行驶速度考虑在内[6, 7]。事实上, PET能够反映冲突的严重性, 但是无法直接建立它与冲突严重性的关系。利用微观仿真可以在规划阶段对交叉口的设计进行安全评估。陈永恒等[8]分析了行人过街过程中受到左转机动车干扰后的轨迹和速度等参数的变化规律。郭宏伟等[9]利用非参数形式和参数形式的基准危险函数框架分析了违章行人过街行为, 指出非参数形式模型对行人过街等待行为描述更为精确。随后, 一些研究建立了车辆让行行为的经验模型[10], 利用Logit和Probit模型建立了人行横道处机动车的让行决策模型。Logit间隙接受理论和Probit模型能够将周围车辆和交通条件考虑在内, 从概念上来说, 这些模型可以利用随机分布表示驾驶员的个体差异行为, 但是, 这些模型也未考虑车辆速度的影响, 而速度是评价行人安全的关键因素。

Wang等[11]发现当车辆速度提高时, 事故更加容易发生, 因此, 使用车辆在人行横道处的速度来判断冲突严重性是合理的。Alhajyaseen等[12]分析了左转车辆与行人的相互作用机理, 建立了考虑行人行走方向的左转车辆的间隙接受模型。在上述研究基础上, 文献[13, 14]又建立了转弯车辆的轨迹和速度模型, 模型包含交叉口的几何条件等因素。然而, 转弯车辆的轨迹和速度模型都只适用于自由流交通条件, 并且没有考虑行人的影响。随后, Alhajyaseen等[15]整合了这些模型, 重现了左转车辆和行人之间的冲突机制, 并给出了更为可靠的行人安全评估方法。进而, 他们指出行人行为也是导致行人安全问题的关键因素。道路使用者通常能够通过预测其他道路使用者的行为来避免冲突, 行人行为受交叉口几何条件、信号灯以及周围环境影响。行人的行为由位置和运动速度共同决定, Zhang等[16]分析了行人过街速度, 指出行人速度随着信号的释放而增大。目前, 关于行人与转弯车辆冲突的研究集中在冲突概率、冲突严重性以及冲突的影响因素(例如行人速度、车辆速度等)等方面, 而对行人位置的研究较少。因为广泛分布的行人尤其是违章过街行人会导致行人与转弯车辆冲突点的广泛分布, 而且行人的出现时间和位置都显著影响冲突的概率和严重性, 因此需要进一步研究行人(包括违章行人)过街穿越位置的时空分布。

基于此, 本文利用视频处理技术, 获取过街行人的全时空信息, 提取行人(包括违章行人)的过街轨迹, 总结了行人位置随时空的变化规律, 并利用实际调查数据, 定量分析了人行横道长度和绿灯消散时间对行人过街位置的影响。基于行人时空位置分布规律, 分析了行人与转弯车辆的冲突点分布区域。

1 数据采集和分析

每个时刻行人在人行横道上的位置分布决定着行人与转弯车辆冲突区域的大小, 因此, 本文尝试对每个时刻行人在人行横道上的位置分布进行建模。信号交叉口人行横道的长度和绿灯消散时间是影响行人行走位置的关键因素。为了分析这些因素对行人过街位置的影响, 本文利用视频跟踪技术, 获取了4个信号交叉口共7条人行横道上不同行人(包括违章行人)整个过街过程中每个时刻的位置坐标, 分析了行人过街位置随时间的变化规律。

1.1 调查地点

所有调查信号交叉口均位于商业中心, 并且周围存在着公交站点、小商店和大型商场, 保证足够的行人样本量。调查时间选择为下午13:00~15:30(连续2天), 因为这段时间内商业中心的人流量最大。利用视频跟踪技术对行人过街每个时刻的位置信息进行采集, 获取行人的全时空交通数据, 进而对行人过街位置进行建模。7个调查地点的几何条件如表1所示。

表1 调查地点的几何条件 Table 1 Geometric characteristic of study sites
1.2 分析方法和定义

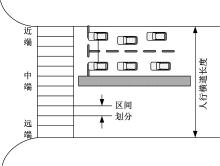
人行横道长度l的定义如图1所示。行人过街时, 随绿灯时间的消散, 行人速度越来越大, 行人在人行横道上也越来越分散。远端表示行人和转弯车辆存在冲突的一端。当近端行人到达人行横道中部以后, 如果在远端并没有机动车停放, 行人会选择最短路径过街, 因此发生违章过街。根据行人过街过程中的移动位置数据, 分析每个时刻人行横道上每个定义区间内所有行人的平均穿越位置, 以此对行人过街的穿越位置进行建模。将行人绿灯开始释放时刻记为绿灯消散时间0点, 随着绿灯的释放, 绿灯消散时间t增大。

图1 人行横道长度定义Fig.1 Definition of crosswalk length

2 模型建立
2.1 行人与转弯车辆冲突区域分析

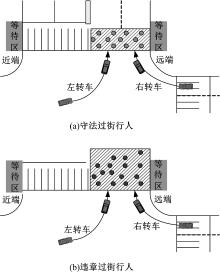
在行人的安全问题中, 行人与转弯车辆的冲突尤为突出, 尤其是行人违章过街导致行人与转弯车辆冲突区域扩大, 广泛的冲突区域导致广泛分布的冲突点, 如图2所示。

图2 行人与转弯车辆的冲突示意图Fig.2 Schematic of conflict between turning vehicles and pedestrians

在行人绿灯期间, 行人每个时刻的过街位置都会受到多种因素(例如绿灯消散时间t、人行横道几何条件、其他过街行人以及转弯车辆等)的影响。因为行人的穿越位置受行走方向的影响, 所以需要把两个方向的行人分开进行研究, 本文只集中于研究从近端到远端行走的行人, 这是因为, 这部分行人在穿越过中央分隔带后, 一部分行人开始采取最短路径过街, 导致行人与转弯车辆的冲突区域扩大。

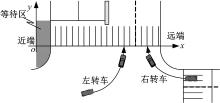
在分析行人位置分布之前, 首先需要建立坐标系, 以此表示行人位置的变化, 如图3所示。为观察行人在行人红灯期间的等待位置, 将坐标系的原点定义在距离人行横道近端5 m处的o点。绿灯消散时间也是影响行人行走位置的重要因素, 随着绿灯时间的消散, 行人速度逐渐增大, 行人也逐渐变得分散。

图3 坐标系示意图Fig.3 Schematic of coordinate

行人可以分为守法行人和违章行人。在过街末期, 无论是守法过街行人还是违章行人, 都会与转弯车辆形成冲突。违章过街行人与转弯车辆的冲突发生在人行横道外, 扩大了它们之间的冲突范围, 增加了行人和转弯车辆的干扰时间, 对行人安全造成了威胁。如图4所示, 违章过街行人在过街末期, 为选择最短路径过街, 通常会在人行横道外部行走, 这直接导致行人和转弯车辆冲突区域的扩大, 冲突点也随之分散, 人车冲突时间变长。

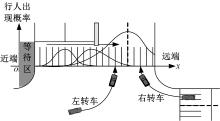
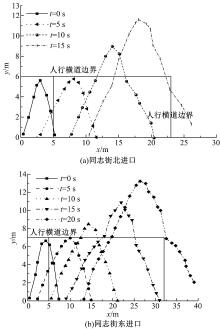
图4 不同时刻行人过街位置分布图Fig.4 Pedestrians crossing positions distribution diagram at different moments

2.2 行人位置分析

为分析行人不同时刻行走位置的分布规律, 将人行横道(包括等待区)划分为N个相同区间。国标[17]规定人行横道线的线宽为40或45 cm, 线间隔一般为60 cm, 为便于统计, 本文利用人行横道标线, 将横道分为多个宽度相似的区间, 如图2所示, 分别统计同一区间所有行人位置坐标x、y的平均值, 进而得到行人在人行横道上的行走位置分布, 如图5所示。

图5 人行横道不同时刻行人过街位置分布Fig.5 Pedestrians crossing positions distribution at different moments

从图5(a)(b)可知, 在观测时间内, 随消散时间的增加, 行人位置分布向行人行走方向移动, 且绿灯消散时间越大, 行人位置越分散, 行人过街位置分布形状变得更宽。此外, 因为部分行人违章过街, 行人行走位置的峰值也逐渐增加。对比图5(a)和图5(b), 在同一绿灯消散时刻, 人行横道越短, 行人位置分布越集中, 这是因为当人行横道较短时, 行人行为的波动性较小, 行人行走更为稳定。当t=0时, 行人处于等待区, 少数行人进入人行横道。

2.3 行人与转弯车辆冲突区域分布模型

分析行人位置分布图形, 需要选择一个峰值函数进行建模, 并且, 函数峰值和范围能够通过调整模型参数实现, Gauss函数能够满足上述条件。Gauss函数模型中, 包含w、xc和A三个基本参数, 通过调整3个参数的值可以表示不同形状的峰值函数图形, 如图6所示。根据观测行人的位置分布规律,

选择Gauss函数来建立行人位置的分布模型。本文希望建立参数w、xc和A与消散时间t和人行横道长度l的函数关系, 进而对行人位置分布进行建模。Gauss函数的函数表达式如式(1)所示:

y=Aw2πexp-2x-xcw2（1）

式中:y、x为行人位置的y和x坐标值; A、w、xc均为Gauss参数。

图6 不同参数下的Gauss函数Fig.6 Gauss function with different parameters

建立参数A、w和xc与消散时间和人行横道长度的函数关系, 如式(2)(3)(4)所示:

A=a1t+b1l+c1(2)w=a2t+b2l+c2(3)xc=a3t+b3l+c3(4)

式中:t为绿灯消散时间, s; l为人行横道长度, m; a1、b1、c1、a2、b2、c2、a3、b3、c3为模型相关系数。

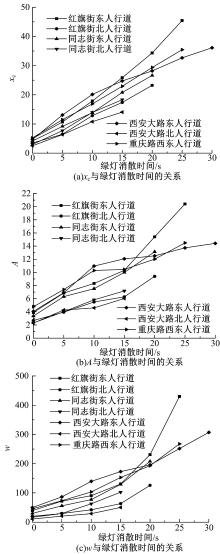
为了分析函数参数w、xc和A的变化趋势, 调查了不同人行横道长度条件下, 绿灯消散时间与3个参数的关系, 结果如图7所示。从图7可以看出, 3个参数均随着绿灯消散时间的增加而增大。同理, 图8表明:3个参数均随着人行横道长度的增加而增大。这就解释了随着绿灯消散时间和人行横道长度的增加, 行人行走位置分布越来越分散, 行人位置分布峰值越来越大。需要注意的是, 本文也对行人需求和等待行人数量做了与图7相同的分析, 结果显示, 参数随行人需求和等待行人数量的变化呈现无规律的波动, 反映在模型中即为R2均小于0.2, 因此行人需求和等待行人数量在模型建立过程中并未被当作模型参数。

图7 绿灯消散时间t与3个参数的关系Fig.7 Relation between three parameters and elapsed time t

图8 人行横道长度与3个参数的关系Fig.8 Relation between three parameters and crosswalk length

经过多元回归分析, 可以确定式(2)(3)(4)中的系数, 因此式(2)(3)(4)可以表示为(5)(6)(7):

A=6.9t+2.64l-58.6(5)w=0.4t+0.15l-1(6)xc=1.14t+0.24l-3.37(7)

其中式(5)(6)(7)的R2分别为0.9、0.93和0.97, 表明模型能够很好地表示参数w、xc和A随绿灯消散时间和人行横道长度的变化规律。实际应用中, 根据绿灯消散时间以及人行横道长度即可确定在某一时刻行人在人行横道上的位置分布规律, 这有利于判断行人和转弯车辆的冲突区。

3 模型验证及应用
3.1 实际观测与理论结果对比

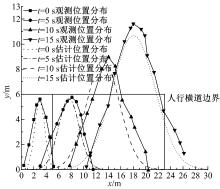
为了验证模型的准确性, 需要将理论计算的行人穿越位置分布与实际行人穿越位置分布进行对比。经过分析, 验证地点选择在同志街与自由大路交叉口北进口处人行横道, 对比实际观测的不同绿灯消散时刻行人到达位置分布图形和模型计算的不同绿灯消散时刻行人到达位置分布图形, 如图9所示。在置信水平为95%条件下, 模型通过了T检验, 结果表明:估计的行人位置分布与实际观测位置分布并无显著差异。本文所建立的模型可以用来描述行人过街时在人行横道上的位置分布规律。

图9 观测行人位置分布与估计行人位置分布对比Fig.9 Observed pedestrians crossing positions distribution versus estimated pedestrians crossing positions distribution

3.2 模型应用

本文建立行人穿越位置分布模型的目的是为了判断有违章行人存在条件下行人与转弯车辆的冲突区域, 进而根据冲突范围确定合理的优化方法限制行人违章并减少行人与转弯车辆的冲突。如图1(b)所示, 违章行人导致了行人与转弯车辆冲突区域增大, 进而导致广泛分布的人车冲突点, 严重威胁了行人的安全。本文建立的行人位置分布模型能够指导行人安全设施(例如行人安全护栏)的设置, 如图10所示, 通过设置护栏降低违章发生的概率, 减小冲突区域, 以此保证行人过街的安全和提高信号交叉口的运行秩序。

图10 行人安全护栏设置Fig.10 Pedestrian safety barrier setting

4 结束语

利用视频处理技术对信号交叉口过街行人的全时空数据进行采集, 考虑了违章行人对行人位置分布的影响, 分析了存在违章行人条件下, 行人与转弯车辆冲突区域的变化机理, 研究了行人位置分布的内在规律。主要研究结论有:违章行人导致行人与转弯车辆冲突区域扩大, 冲突点分散; 行人过街位置随绿灯消散时间和人行横道长度的增加逐渐分散, 同时, 冲突范围扩大; 考虑绿灯消散时间和人行横道长度对行人位置分布的影响, 建立了行人位置分布模型; 在行人位置分布模型的基础上对模型的潜在应用进行了分析。因此, 针对行人违章发生频率较高的交叉口, 除了加大安全教育管理外, 可以考虑设置封闭护栏等手段优化人行横道设计以限制违章发生, 利用所建立模型判定行人与转弯车辆的冲突范围, 根据冲突范围确定合理的封闭护栏设置方法, 同时对于交叉口冲突特别严重的交叉口, 也可以考虑分离行人和转弯车辆的相位, 以此避免行人与转弯车辆冲突的发生。

The authors have declared that no competing interests exist.

参考文献
[1] Chen P, Nakamura H, Asano M. Application of surrogate safety measures for assessment of pedestrian versus left-turning vehicle conflict at signalized crosswalks[J]. Advances in Transportation Studies, 2014, 1(Special): 37-50. [本文引用:1]
[2] Perkins S R, Harris J L. Traffic conflict characteristics-accident potential at intersections[J]. Highway Research Record, 1968(225): 35-43. [本文引用:1]
[3] Allen B L, Shin B T, Cooper P J. Analysis of traffic conflicts and collisions[J]. Transportation Research Record, 1978(677): 67-74. [本文引用:1]
[4] Gettman D, Head L. Surrogate safety measures from traffic simulation models[J]. Transportation Research Record, 2003(1840): 104-115. [本文引用:1]
[5] Tang K, Nakamura H. Safety evaluation for intergreen intervals at signalized intersections based on probabilistic method[J]. Transportation Research Record, 2009(2128): 226-235. [本文引用:1]
[6] Kruysse H W. The subjective evaluation of traffic conflicts based on an internal concept of dangerousness[J]. Accident Analysis & Prevention, 1991, 23(1): 53-65. [本文引用:1]
[7] Tiwari G, Mohan D, Fazio J. Conflict analysis for prediction of fatal crash locations in mixed traffic streams[J]. Accident Analysis & Prevention, 1998, 30(2): 207-215. [本文引用:1]
[8] 陈永恒, 尉明丽, 曲昭伟, 等. 信号交叉口左转车干扰下的行人过街特性[J]. 吉林大学学报: 工学版, 2015, 45(1): 62-67.
Chen Yong-heng, Wei Ming-li, Qu Zhao-wei, et al. Pedestrian crossing characteristics under influence of left-turn vehicle[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(1): 62-67. [本文引用:1]
[9] 郭宏伟, 高自友, 赵小梅. 基于持续模型的行人过街行为[J]. 吉林大学学报: 工学版, 2009, 39(增刊2): 35-40.
Guo Hong-wei, Gao Zi-you, Zhao Xiao-mei. Pedestrian crossing behaviours based on duration model[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(Sup. 2): 35-40. [本文引用:1]
[10] Sun D Z, Ukkusuri S V, Benekohal R F, et al. Modeling of motorist-pedestrian interaction at uncontrolled mid-block crosswalks[J]. Urbana, 2002, 51: 61801. [本文引用:1]
[11] Wang X, Abdel-Aty M. Analysis of left-turn crash injury severity by conflicting pattern using partial proportional odds models[J]. Accident Analysis & Prevention, 2008, 40(5): 1674-1682. [本文引用:1]
[12] Alhajyaseen W K M, Asano M, Nakamura H, et al. Gap acceptance models for left-turning vehicles facing pedestrians at signalized crosswalks[C]//Proceedings of the 3rd International Conference on Road Safety and Simulation, Indiana, 2011: 01506156. [本文引用:1]
[13] Asano M, Alhajyaseen W K M, Suzuki K, et al. Modeling variation in the trajectory of left-turning vehicles considering intersection geometry[C]//90th Transportation Research Board Annual Meeting, Washington, DC, 2011: 01336739. [本文引用:1]
[14] Wolfermann A, Alhajyaseen W K M, Nakamura H. Modeling speed profiles of turning vehicles at signalized intersections[C]//3rd International Conference on Road Safety and Simulation, Indianapolis, 2011: 01506194. [本文引用:1]
[15] Alhajyaseen W K M, Asano M, Nakamura H. Estimation of left-turning vehicle maneuvers for the assessment of pedestrian safety at intersections[J]. IATSS Research, 2012, 36(1): 66-74. [本文引用:1]
[16] Zhang X, Nakamura H, Iryo-Asano M, et al. Modeling pedestrian speed at signalized crosswalks considering crosswalk length and pedestrian signal timing[J]. Infrastructure Planning Review, 2014, 70(5): 1031-1040. [本文引用:1]
[17] GB5768. 3-2009. 道路交通标志和标线[S]. [本文引用:1]