随着危险品运输量的逐年增长, 对危险品运输的研究逐渐成为一个热点。Erkut等^[1]在2007年详细剖析了危险品运输这个概念, 阐述了危险品的主要分类、发生事故的主要地点, 同时描述了危险品运输带来的各种影响以及各种影响的计算模型等。近年来, 较为成熟的研究主要集中于路径问题(LP), 车辆规划问题(VSP)和路径车辆规划问题(LSP)三个方面。LP可描述为选择一系列的点, 从这些点中构造一系列的路径, 以最少的成本服务于一系列的危险品需求点^[2]。典型的VSP问题可描述为一辆车如何在规定的时间内分配给多条路径^{[3, 4, 5]}, Clautiaux等^[6]首次引用了多辆车如何在规定的时间内分配给多条路径, 完成运输任务。王云鹏等^[7]使用Arc GIS对整个长春市的危险品运输进行了路径优化。LSP是LP与VSP的结合, 前者主要决定危险品的仓库地址, 后者决定车辆的规划问题。在危险品领域, 鉴于危险品概率低、风险大的特点, 一般将LP与VSP结合在一起, 同时考虑。

遗传算法是一种通过模拟自然进化过程搜索最优解的方法, 应用领域广泛, 不仅适用于危险品运输, 在交通运输的各种领域中均有涉猎。Yang等^[8]利用遗传算法对地铁系统的时刻表进行优化。Nayeem等^[9]介绍了遗传算法的各种版本, 并主要针对交通网络, 利用遗传算法求解交通运输时间最小优化模型。Bielli等^[10]利用遗传算法优化了公交车网络。

从现有研究成果来看, 针对车辆调度方面的研究较少。基于此, 本文提出了一种危险品运输车辆调度模型, 在运输路径已规划完全的前提下, 考虑如何合理安排车辆顺序, 有一定的创新性和实用性。根据所建模型中每个货物需求点派送次数不固定的特点, 在设计染色体编码时, 使用多层编码对实例问题进行求解验证, 结果表明该算法具有良好的性能。

运输危险品货物的车辆均为危险品专用车辆, 其线路均是符合车辆运输通行的公路或者城市道路。危险品需求点的货物需求量有一定的规律, 历年来相同时间、相同周期(如一个星期或者一个月)内, 危险品货物的需求量基本保持平衡。

车辆调度问题从数学上可以描述为有n个需要危险品货物的地点要使用v辆车进行派送, 而在周期性派送货物过程中, 每一个周期需要往危险品需求点派送m次, 车辆调度的数学模型描述如下:

(1)车辆集V={v₁, v₂, …, v_m}, v_j为第j台车辆, j=1, 2, …, m。

(2)危险品需求地点集S={s₁, s₂, …, s_n}, s_i为第i个危险品需求地点, i=1, 2, …, n。

(3)调度车辆序列集OV={ov₁, ov₂, …, ov_n}, ov_i={ov_i1, ov_i2, …, ov_ik}为派送至需求地点s_i的车辆在总的车辆调度序列中的序列。

(4)可选车辆集OPV={ov_i1, ov_i2, …, ov_ik}, ov_ij={ov_ij1, ov_ij2, …, ov_ijk}为需求点s_i第j次运送危险品可选的车辆。

(5)使用车辆派送至危险品需求点的时间矩阵T, t_ij∈ T, t_ij为第i个危险品需求地点s_i使用第j辆车的时间。

(6)仓库到各个危险品需求点的距离矩阵D, d_i∈ D, d_i为仓库到第i个危险品需求点的距离。

(7)使用车辆派送至危险品需求点的速度矩阵V', v_ij∈ V', v_ij为第i个危险品需求地点s_i使用第j辆车的速度。

本模型以周期性派送危险品货物的总在途时间为目标函数, 长期观察和统计每次派送至危险品需求点所使用的车辆和时间, 得到对应的车辆矩阵和时间矩阵如下所示:

minTsum=∑i=1n∑j=1mtij(1)tij=divij(2)s.t.tij∈T, i=1, 2, …, n ; j=1, 2, …, m(3)ovij∈OPV(4) i=1, 2, …, n; j=1, 2, …, mvij≤80kmh(5)OPV⊂V(6)l≥2(7)

式中:T_sum为所有派送时间的总和; t_ij为第i个危险品需求地点s_i使用第j辆车的时间。

式(2)为时间的计算公式; 式(3)表示t_ij来源于时间矩阵T; 式(4)为每次派送货物可使用的车辆集; 式(5)为车辆速度需满足的条件; 式(6)表示可用车辆集是所有车辆的子集; 式(7)表示每个需求点需要的派送次数不止一次。

采用多层编码遗传算法求解周期性危险品运输车辆调度问题, 假设共有6个危险品运输需求点, 分别是需求点1~需求点6, 通过10辆车进行危险品派送, 通过长期的统计发现, 在一个周期内分别需要往6个需求点运送5次, 由于每次危险品的容量不同, 可供选择派送的车辆也不固定, 每次派送可供选择的车辆如表1所示。

如表1所示, 第1行第1列的内容是3, 表示需求点1的第1次派送可使用的车辆是车辆3。第2行第4列的内容是[6, 7], 表示需求点4的第2次派送可使用的车辆是车辆6或者车辆7。对应的每次派送危险品所使用的派送车辆的派送时间如表2所示。

表1

Table 1

表1(Table 1)

表1 派送车辆 Table 1 Delivery vehicles 派送次数 需求点 1 2 3 4 5 6 第1次 3 6 4 [2, 9] [3, 7] 5 第2次 4 [3, 8] 5 [6, 7] 5 [1, 10] 第3次 2 [6, 4] 7 [2, 1] [4, 10] 5 第4次 5 6 [4, 7] 10 [2, 5] [3, 6] 第5次 [4, 5] 3 [9, 10] 6 2 [3, 8]

表1 派送车辆 Table 1 Delivery vehicles

表2

Table 2

表2(Table 2)

表2 派送时间 Table 2 Delivery time h 派送次数 需求点 1 2 3 4 5 6 第1次 4 6 7 [7, 3] [3, 4] 9 第2次 5 [2, 6] 3 [1, 4] 2 [3, 3] 第3次 3 [5, 3] 6 [2, 6] [7, 8] 1 第4次 2 3 [4, 6] 2 [1, 4] [3, 5] 第5次 [5, 4] 8 [7, 9] 6 5 [3, 4]

表2 派送时间 Table 2 Delivery time h

如表2所示, 第1行第1列的内容是4, 表示需求点1的第1次派送使用车辆3的派送时间是4 h。第2行第2列的内容是[2, 6], 表示需求点2的第2次派送可使用的车辆是车辆3和车辆8, 使用车辆3的派送时间是2 h, 使用车辆8的派送时间是6 h。

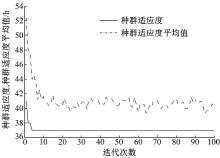
多层编码遗传算法的基本参数设置如下:种群数目为40; 最大迭代次数为100; 交叉概率为0.8; 变异概率为0.2。种群适应度值变化如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 种群适应度值变化Fig.1 Population fitness value variation

从图1中可以看出:随着迭代次数的增加, 种群的适应度值包络趋于稳定。经过100次迭代后, 种群的适应度值趋于40 h; 种群适应度平均值也趋于稳定, 表明多层编码遗传算法能有效地解决危险品运输车辆的调度问题。

图2为危险品运输车辆调度的甘特图。图中的3位数表示车辆调度情况, 例如501表示需求点5的第1次派送危险品。图中的0~5 h内可分别实现需求点3的第1次派送, 需求点1的第1次派送, 需求点2的第1次派送, 需求点5的第1次派送等, 以此类推。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 车辆调度的甘特图Fig.2 Gantt chart of vehicle scheduling

针对危险品实际运输时不同容量需要使用不同车辆, 在周期性时间段内需要的次数不固定, 以及不同车辆的运输时间不同等特性, 对车辆调度进行建模, 并利用多层编码遗传算法进行求解, 力求达到运输调度总时间最少的目标。最后, 通过Matlab仿真验证了该算法的可行性。