城市轨道交通与地面公交竞合关系演化机制

引用本文

赵学彧, 杨家其, 彭亚美. 城市轨道交通与地面公交竞合关系演化机制. 吉林大学学报(工学版), 2017, 47(3): 756-764
ZHAO Xue-yu, YANG Jia-qi, PENG Ya-mei. Competitive and cooperative relationship evolution mechanism between urban rail transit and traditional bus. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 756-764 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703010
Permissions

城市轨道交通与地面公交竞合关系演化机制

赵学彧, 杨家其, 彭亚美

武汉理工大学交通学院,武汉430063

作者简介:赵学彧(1986-),男,博士研究生.研究方向:城市轨道交通.E-mail:591949181@qq.com

基金项目:国家自然科学基金项目(51279153)

摘要

为了揭示城市轨道交通与地面公交之间的竞争合作的演化特点,构建了城市交通客流自组织系统的演化模型。在此基础上,构建了城市轨道交通与地面公交之间的竞合机制模型,分析了两种方式共存时产生的竞合效应,以及在各竞合时期的关系演化机制。最后,以武汉市为例,分析了两种方式在不同时期的竞合关系演化态势,得到各时期下城市公共交通竞合效应发展特征和相应策略。本文研究成果对城市轨道网络与地面公交的规划和发展有显著的实践意义。

关键词: 交通运输系统工程; 城市轨道交通; 自组织演化; 竞合效应; 竞合关系; 演化机制

中图分类号:U121 文献标志码:A 文章编号:1671-5497(2017)03-0756-09

Competitive and cooperative relationship evolution mechanism between urban rail transit and traditional bus

ZHAO Xue-yu, YANG Jia-qi, PENG Ya-mei

School of Transportation, Wuhan University of Technology, Wuhan 430063, China

Abstract

To reveal the competition and cooperation evolution mechanism between urban rail transit and traditional bus, the evolution model of the self-organization systems in urban passenger transport flow is constructed. On this basis, the competition model consisting of urban rail and traditional bus is established with the coexistence of both competitive effect and cooperative effect. Finally, as a case study, the evolution mechanism in different stages in Wuhan city is analyzed. The development feature of the competitive and cooperative effects of urban public transit at each stage is obtained and corresponding strategy is illustrated. This study provides a reference for the planning and development of urban rail transit and public bus networks.

Key words: engineering of communication and transportation system; urban rail transit; self-organization evolution; competitive and cooperative effect; competitive and cooperative relationship; evolution mechanism

Show Figures

0 引言

城市轨道交通在城市客运系统中具有支柱地位, 但在其发展过程中, 由于其实际运送的客流量与预测客流量差距较大, 无法完全发挥城市客运的主干作用。因此, 城市客运主要由轨道和常规地面公交共同完成。但作为两种功能各异的城市公交模式, 如何处理二者关系, 使其协同运营, 共同提高效率, 合理分配客源份额, 从而提高运输效率成为国内外学者的研究热点, 而二者竞合机制更是其中最重要的研究对象。

Tabuchi^[1]分析了各种付费方式下交通方式间的竞争机制。Hollander等^[2]发现促使交通方式间争夺客源的原因是各经营者追求自身收益最大化。刘华胜^[3]研究了轨道交通建成或运营时与地面公交之间相关的站点、网络优化, 运营协调与突发事件应急联动等关键问题。李橘云^[4]从时间、费用和需求等角度分析了轨道交通主干线上两类公共交通方式的主要客流竞争范围, 提出接驳线路优化调整对策。唐文彬等^[5]提出了方式间竞合理论框架, 以出行时间和综合成本为目标, 分析了公共交通与非机动车及私家车间的竞争关系。黄建中等^[6]分析了上海轨道交通6号线对出行时间和费用的影响, 构建了城市公交系统效用函数, 分析了两种公交方式之间的竞合关系, 构建了客流选择模型。孙杨等^[7]以复杂网络为手段, 研究了市内公交与其他客运方式, 特别是轨道交通的竞合模式。马天山等^[8]分析了轨道交通与地面公交之间的换乘优化模型。张杰林等^[9]研究了在共线的前提下, 轨道交通与地面公交在经营模式和客源分配上的竞争。Mohaymany等^[10]采用蚁群算法分析并优化了多方式的城市接运网络, 强调了多方式的协同。

回顾国内外相关研究, 诸多学者针对城市轨道交通与地面公交的竞争机制研究更加侧重于某一个特定的策略或服务。但在现实情形下, 城市轨道交通与地面公交的竞争更多集中在客源的争取上, 而这涉及到轨道交通自身增长能力及城市内其他客运方式对其的影响作用。并且在路网尚未完全形成之前, 轨道交通不可能完全取代地面公交成为主干方式, 而只可在主干道发挥优势, 这主要表现在各自发展过程中, 轨道交通与地面公交二者竞合关系的演化。此外, 与其他双方式竞合模型所探讨的前提不同, 在轨道交通作为新兴的公交出行方式进入市民日常生活之前, 市民早已习惯于以地面公交为主导的公共交通出行方式, 因此地面公交具备稳定而垄断的客源。轨道交通以其大运量、高速度的优势形成强势竞争力, 与地面公交争夺客源。此后两种方式不断在票价、运量、站间距和路线等相关方面调整策略, 争取更多的客源份额, 因此展开竞争; 随着双方服务水平的上升, 客流需求也会不断增加, 双方会展开换乘衔接方面的合作。基于以上考虑, 双方存在着竞合关系的特殊演化过程, 这也是国内外研究少有涉及的方面。

本文引入城市公交系统的自组织演化理论, 建立了由轨道交通和地面公交组成的两种方式竞合演化模型。分析了自轨道交通进入城市公交体系之后, 两种方式在竞争以及合作两种效应下的系统稳定性和竞合关系演化过程。最后, 以武汉市公交客运系统整体客流发展为实例背景, 发掘客流量增长规律, 并分析了双方竞合关系在不同时期的演化机制。

1 基于自组织演化的轨道交通与地面公交的竞合模型

1.1 城市公共客运系统自组织演化的假设

总体而言, 一般类型城市公共客运交通系统的自组织演化来自于其系统内、外竞争和自身协调等诸多方面的共同作用^[11]。考虑到现实情况下已然无法全部满足客流系统的演化对空间和资源的需求, 本文对系统做出如下假设:

(1)系统的自组织演化过程会受到系统所处区域和时间的相关条件约束, 包括但不限于当地经济发展水平、集疏运条件、人口和土地资源等因素。

(2)设定系统自身生长率为常数。

(3)系统自组织演化过程的影响因素除自身生长率外, 还有来自外部环境的竞争因素。

(4)由于影响因素对系统自组织演化的阻滞作用, 系统自组织演化过程可采用Logistic方程^[11]来描述。

1.2 轨道交通和地面公交的自组织演化模型

作为城市公共客运交通的一部分, 轨道交通系统的客流自组织演化机制也继承其系统演化的主要特征。同时, 考虑到轨道交通系统的客流自组织系统存在随时间变化的动态特性, 故本文采用自组织演化模型, 分析城市轨道客流量的变化规律, 如式(1)所示:

$\frac{d Q}{d t} = G (Q) + θ (t)$ （1）

式中:Q为城市轨道交通的客流量随时间变化函数; G(Q)为城市轨道交通系统随客流量变化函数; θ (t)为随机函数, 体现了城市轨道交通客流量变化的随机性。因为城市客运交通系统除轨道交通系统以外, 还存在其他交通方式的作用。

基于以上假设和动态方程参数定义, 结合市内交通出行需求和市区人口的增长规律, 可依照Logistic模型改进城市轨道交通系统自组织演化模型, 如式(2)所示:

$\frac{d Q_{t}}{d t} = r_{t} Q_{t} (t) [1 - η_{ti} Q_{i} (t)]$ （2）

式中:Q_t、Q_i分别为城市轨道交通和地面公交系统客流量随时间的变化函数; r_t为城市轨道交通客流量年平均增长率; η _ti为影响因子, 体现了地面公交系统对城市轨道客运量的影响程度, 主要表现在地面公交系统客运量增长对轨道交通的抑制作用。

同理, 对于地面公交的自组织演化机制, 调整参数r_t为r_i, η _ti为η _it, 可推理相应的自组织演化模型, 如式(3)所示:

$\frac{d Q_{i}}{d t} = r_{i} Q_{i} (t) [1 - η_{it} Q_{t} (t)]$ （3）

1.3 轨道交通和地面公交的竞合微分方程模型

联立式(2)(3), 可组成两种方式客流竞合微分方程模型, 如方程(4)所示, 该模型表征了两种方式竞合关系及其演化机制。

$\{\begin{array}{l} \frac{d Q_{i}}{d t} = r_{i} Q_{i} (t) [1 - η_{it} Q_{t} (t)] \\ \frac{d Q_{t}}{d t} = r_{t} Q_{t} (t) [1 - η_{ti} Q_{i} (t)] \end{array}$ （4）

当t® ¥ 时, 竞合系统趋于稳定, 此时可得系统定态竞合模型, 即:

$\{\begin{array}{l} f (Q_{t}, Q_{i}) = d Q_{t} / d t = r_{t} Q_{t} (t) [1 - \\ η_{tt} Q_{t} (t) - η_{ti} Q_{i} (t)] \\ g (Q_{t}, Q_{i}) = d Q_{i} / d t = r_{i} Q_{i} (t) [1 - \\ η_{ii} Q_{i} (t) - η_{it} Q_{t} (t)] \end{array}$ （5）

为了对轨道交通和地面公交的竞合演化趋势进行分析, 可对式(5)参数做出改进。

对于城市客运系统而言, 影响因子η _it的大小所涉及的因素包括该方式的规模、服务水平与运输能力。从自组织理论角度分析认为, 在一定时间内, 客运方式系统发展趋势的决定性因素是其能容纳的最大客流量N_t, 且该因素的增长会对系统发展产生抑制作用。

同时, 地面公交系统的客流对城市轨道交通系统客流的影响力因子体现出来的竞合效应也与轨道交通系统最大客流量有关。因此将系统容纳的最大客流量导入式(5), 则可得到式(6):

$\{\begin{array}{l} f (Q_{t}, Q_{i}) = \frac{d Q_{t}}{d t} = \\ r_{t} Q_{t} (t) (1 - \frac{Q_{t} (t)}{N_{t}} - \frac{α_{ti} Q_{i} (t)}{N_{i}}) = 0 \\ g (Q_{t}, Q_{i}) = \frac{d Q_{i}}{d t} = \\ r_{i} Q_{i} (t) (1 - \frac{α_{it} Q_{t} (t)}{N_{t}} - \frac{Q_{i} (t)}{N_{i}}) = 0 \end{array}$ （6）

式中:N_t、N_i分别为轨道交通和地面公交发展的最大客流容量; α _ti为地面公交对轨道交通客流量的影响; α _it为轨道交通对地面公交客流量的影响。当参数α _ti和α _it大于0时, 二者存在竞争关系; 否则为合作关系。事实上, 参数α _ti和α _it也可体现为两种方式各自的竞争力度, 主要反映在双方自身的竞争力(主要为营运能力)、竞争意愿和竞争策略等方面。如果α _ti或α _it在0到1之间, 则竞争力度处于弱水平; 如果α _ti或α _it大于1, 则竞争力度处于强水平。

2 竞合效应及关系演化机制

2.1 竞争效应

方程(6)表征了轨道交通和地面公交的竞合演化关系。当t® ¥ 时, 两种方式的竞合演化达到稳定状态。然而竞合演化系统稳定趋势是如何演化的, 其演化结构是如何变化的, 对这些问题的研究可为客流管理策略提供理论依据。

在方程(6)中, 当α _it> 0且α _ti> 0时, 该模型表现为竞争效应, 当t® ¥ 时, 竞争系统达到均衡状态, 则可计算得到竞合演化的4个均衡点为:

$[\begin{array}{l} P_{1} \\ P_{2} \\ P_{3} \\ P_{4} \end{array}] = [\begin{array}{l} 0 & 0 \\ N_{t} & 0 \\ 0 & N_{i} \\ N_{t} \frac{1 - α_{ti}}{1 - α_{it} α_{ti}} & N_{i} \frac{1 - α_{it}}{1 - α_{it} α_{ti}} \end{array}]$ （7）

相应的雅可比矩阵表现形式为:

$\begin{array}{l} A = [\begin{array}{l} f_{Q_{t}} & f_{Q_{i}} \\ g_{Q_{t}} & g_{Q_{i}} \end{array}] = \\ [\begin{array}{l} r_{t} (1 - \frac{2 Q_{t} (t)}{N_{t}} - \frac{α_{ti} Q_{i} (t)}{N_{i}}) & \frac{- r_{t} α_{ti} Q_{i} (t)}{N_{i}} \\ \frac{- r_{i} α_{it} Q_{t} (t)}{N_{t}} & r_{t} (1 - \frac{α_{it} Q_{t} (t)}{N_{t}} - \frac{2 Q_{i} (t)}{N_{i}}) \end{array}] \end{array}$ （8）

特征方程系数为:

$p = - (f_{Q_{t}}, g_{Q_{i}}) |p_{i}; q = \det A |p_{i}; i = 1, 2, 3, 4$

式中:detA表示A的行列式。

依照微分方程稳定性理论^[12]对均衡点^[13]进行比较分析, 可得两种方式竞争形态模型的均衡点和稳定性, 如表1所示。

表1 竞争形态模型的均衡点和稳定性 Table 1 Equilibrium point and stability of competition morphological model

情况	α _it, α _ti	P₁	P₂	P₃	P₄	t® ¥
(a)	0< α _ti< 1, α _it> 1	不定	稳定	鞍点	-	P₂
(b)	0< α _it< 1, α _ti> 1	不定	鞍点	稳定	-	P₃
(c)	0< α _it< 1, 0< α _ti< 1	不定	鞍点	鞍点	稳定	P₄
(d)	α _it> 1, α _ti> 1	不定	稳定	稳定	鞍点	P₂或P₃
(e)	α _it=α _ti=1	不定	-	-	-	$\frac{Q_{1}}{N_{1}}$ + $\frac{Q_{2}}{N_{2}}$ =-1

表1 竞争形态模型的均衡点和稳定性 Table 1 Equilibrium point and stability of competition morphological model

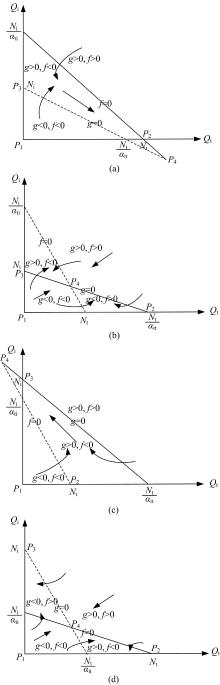
针对(a)~(d)四种竞争情况, 对均衡点进行相平面分析, 如图1所示。

	Figure Option View Download New Window
	图1 不同竞争情况的相平面图Fig.1 Phase plane diagram of different competition scenarios

由图1可见:在情况(a)中, P₂是全局的稳定点, 在t® ¥ 时, 相轨线趋向于P₂点; 在情况(b)中, P₃是全局的稳定点, 在t® ¥ 时, 相轨线均趋向于P₃点。在以上两种情况下, 轨道交通与地面公交之间竞争力相差悬殊, 即强势方会吸引大量客流, 而弱势方被客运市场淘汰; 在情况(c)中, P₄是全局的稳定点, 在t® ¥ 时, 相轨线均趋向于P₄点, 这说明轨道交通与地面公交系统势均力敌, 且竞争力度均不强, 因此双方并无过大冲突, 而竞争较为缓和, 由于双方决策会影响到对方, 因此最终会达到全局稳定的均衡点; 在情况d中, P₂和P₃是局部均衡点, P₄是鞍点, 在该情况中没有全局均衡点。这表明, 两种方式均具有强烈的竞争力度, 且会在客运市场上的客流配额方面形成较为激烈的竞争关系, 两种方式的发展互相产生遏制效应, 因此其竞争的结果具有较大的动态性和不确定性。

综上可见, 轨道交通在单方面有强烈的竞争力度时, 会大量夺取原本属于地面公交的客源; 而地面公交恢复竞争战略, 重新表现出强烈竞争力度时, 双方竞争激烈, 互相遏制对方的发展; 经过一段时间磨合, 双方在势均力敌的情况下均降低竞争力度至弱水平, 因此会达到相对均衡的局面。

根据表1和图1的结果可见, α _it和α _ti的取值可以表现出轨道交通和公交系统相互竞争的激烈程度, 因此需要对两个参数取不同的实际值, 观察双方之间的竞争情况。

2.2 合作效应

当参数α _ti和α _it均小于0时, 该模型表现为合作效应, 此时, 可令β _it=-α _it且β _ti=-α _ti, 当t® ¥ 时, 竞合系统达到稳定状态。此时, β _ti表示地面公交对轨道交通客流量的影响, β _it表示轨道交通对地面公交客流量的影响。同时, 参数β _ti与β _it也可体现为两种方式各自的合作力度, 主要反映在双方自身的合作能力、合作意愿及合作策略等方面。如果β _ti或β _it在0到1之间, 则该方合作力度处于弱水平; 如果α _ti或α _it大于1, 则该方合作力度处于强水平。则可将式(6)转换成式(9), 即:

$\{\begin{array}{l} f (Q_{t}, Q_{i}) = \frac{d Q_{t}}{d t} = \\ r_{t} Q_{t} (t) (1 - \frac{Q_{t} (t)}{N_{t}} + \frac{β_{ti} Q_{i} (t)}{N_{i}}) \\ g (Q_{t}, Q_{i}) = \frac{d Q_{i}}{d t} = \\ r_{i} Q_{i} (t) (1 + \frac{β_{it} Q_{t} (t)}{N_{t}} - \frac{Q_{i} (t)}{N_{i}}) \end{array}$ （9）

由式(9)可得到4个均衡点为:

$[\begin{array}{l} P_{5} \\ P_{6} \\ P_{7} \\ P_{8} \end{array}] = [\begin{array}{l} 0 & 0 \\ N_{t} & 0 \\ 0 & N_{i} \\ N_{t} \frac{1 + β_{ti}}{1 - β_{it} β_{ti}} & N_{i} \frac{1 + β_{it}}{1 - β_{it} β_{ti}} \end{array}]$ （10）

相应的雅可比矩阵的表现形式为:

$\begin{array}{l} B = [\begin{array}{l} f_{Q_{i}} & f_{Q_{i}} \\ g_{Q_{t}} & g_{Q_{i}} \end{array}] = \\ [\begin{array}{l} r_{t} [1 - \frac{2 Q_{t} (t)}{N_{t}} + \frac{β_{ti} Q_{i} (t)}{N_{i}}] & \frac{r_{t} β_{ti} Q_{i} (t)}{N_{i}} \\ \frac{r_{i} β_{it} Q_{t} (t)}{N_{t}} & r_{t} [1 + \frac{β_{it} Q_{t} (t)}{N_{t}} - \frac{2 Q_{i} (t)}{N_{i}}] \end{array}] \end{array}$ （11）

类似于竞争效应的探讨, 两种方式合作形态模型的均衡点和稳定性如表2所示。

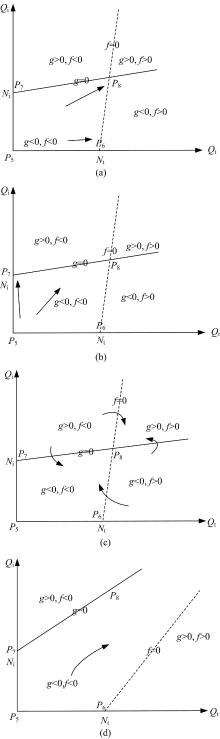
同时针对(a)~(d)四种合作情况, 分别对均衡点进行相平面分析, 其结果如图2所示。

由图2可见:在情况(a)中, P₆是鞍点, 若β _itβ _ti< 1, 则P₈是全局的稳定点。在t® ¥ 时, 相轨线均趋向于P₆或P₈点; 在情况(b)中, P₇是鞍点, 若β _itβ _ti< 1, 则P₈是全局的稳定点。在t® ¥ 时, 相轨线均趋向于P₇或P₈点。在以上两种情况下, 轨道交通和地面公交之间某一方合作积极, 另一方较平缓, 积极的一方通过合作来充分发展, 并可能大幅度超越其自然发展规模极限, 平缓的一方在自身演化过程中无太大影响, 但在演化速度和成长极限方面有所提高; 在情况(c)下, P₈是全局的稳定点, 在t® ¥ 时, 相轨线均趋向于P₈点。这表明轨道交通与地面公交双方营运水平接近, 可通过平等互助形成一个全局稳定的稳定点, 并且该稳定点会超过两种方式自身的发展极限, 因此相互合作是双赢的选择; 而情况(d)没有全局均衡点, 说明两种方式能力都很强, 若达成合作, 双方均会从合作中受到可促使自身和对方发展的影响和作用, 可以得到较高的收益, 但很难形成一个全局稳定的均衡点, 合作竞争演化的结果具有较强的不确定性。

表2 合作形态模型的均衡点和稳定性 Table 2 Equilibrium point and stability of cooperation morphological model

情况	β _it, β _ti	P₅	P₆	P₇	P₈	t® ¥
(a)	0< β _ti< 1, β _it> 1	不定	鞍点	不定	稳定	P₆或P₈
(b)	0< β _it< 1, β _ti> 1	不定	不定	鞍点	稳定	P₇或P₈
(c)	0< β _it< 1, 0< β _ti< 1	不定	不定	不定	稳定	P₈
(d)	β _it> 1, β _ti> 1	不定	不定	不定	不定	-
(e)	β _it=β _ti=1	不定	-	-	-	$\frac{Q_{1}}{N_{1}}$ + $\frac{Q_{2}}{N_{2}}$ =-1

表2 合作形态模型的均衡点和稳定性 Table 2 Equilibrium point and stability of cooperation morphological model

	Figure Option View Download New Window
	图2 不同合作情形的相平面图Fig.2 Phase plane diagram of different cooperation scenarios

综上可见, 当双方在单方面具有强烈的合作力度时, 会积极发展自身客运量, 但并不会影响对方的发展势头; 而当双方均表现出强烈的合作意愿时, 均会从合作中受到可促使自身和对方发展的影响和作用, 造成双赢的局面; 经过一段时间合作发展, 双方发展水平相近且同步, 通过平等互助形成稳定的发展空间。事实上, 双方合作的时候很难出现单方强烈的情形, 由于合作是互利互惠的, 因此更多情形是双方均具有强烈的合作意图而进行协作。

由图2和表2可见, 不同参数取值可以表现出轨道交通和地面公交系统合作的不同程度, 因此可进一步分析参数取不同值时双方合作情况。

2.3 竞合关系演化机制

通过以上对轨道交通与地面公交之间竞争和合作两种不同效应的分析可知, 随着两种方式的共存和互相影响, 两种方式的互动一般会出现4种不同的情景。

结合轨道交通与公交方式自组织演化的特点, 可以发现, 两种方式在自身演化初期时期, 由于自身的成长需求, 至少会有一方会表现出强烈的竞争性, 并由单方竞争性转向双方竞争性, 因此处于热竞争时期(包括局部热竞争时期和全面热竞争时期); 经过一段时间后, 两种方式各自进入发展期, 此时双方竞争矛盾趋于缓和, 竞争则在运输市场与法规允许的前提下以比较温和的方式进行, 该时期可以成为冷竞争时期。经过一定时间的发展, 两种方式会逐渐意识到可通过合作达成自身的目标, 实现双赢的局面。因此两种方式由竞争关系转变成合作关系, 且两种方式的合作会随着运输市场与规则的不断完善, 以及利益的逐步稳定, 合作程度也会由热合作时期逐步转化成冷合作时期。

综上所述, 各时期及其参数设置如表3所示。

表3 各时期及其参数设置 Table 3 Each stage and its parameter settings

3 实例分析

本文以武汉市的城市公交系统为实例, 分析两种方式竞合关系的演化过程, 并通过不同的参数取值, 分析各演化时期内双方客流量的发展, 探讨双方竞合演化关系机制。

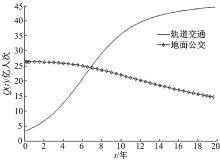
依照2015年统计数据, 武汉市轨道交通共运送乘客3.2亿人次, 而地面公交运送乘客26.3亿人次。依照武汉市轨道交通规划和公交系统客流量历史数据, 以及轨道交通在未来市内客运交通中的主干作用, 可设定轨道交通自身增长率为0.5, 而地面公交自身增长率为0.05。由此定义城市轨道交通发展稳定规模N_t=50亿人次, 地面公交发展规模N_i=30亿人次, 以2015年客运量为初始值, 对各竞合时期的演化机制和客流量增长特点进行分析。

3.1 热竞争时期

在轨道交通刚融入整个城市交通网络时, 其大运量、速度快、延误时间少、服务质量高的特点对整个公交系统带来了冲击, 因此会呈现轨道交通竞争力度大而公交反应较为缓和的局面, 此时为局部热竞争时期。随着时间的推移, 公交系统为应对轨道交通引入带来的客源流失和市场份额降低问题, 开始积极提高自身竞争力, 双方进入全面热竞争时期。

(1)局部热竞争时期

城市轨道交通发展初期, 双方进入局部热竞争时期。由于0< α _ti< 1, α _it> 1, 令α _it=1.2, α _ti=0.2, 则演化趋势如图3所示。由图3可见, 轨道交通的客运量迅速增长, 并接近自身的稳定客运量; 而受其影响和冲击, 地面公交的客运量迅速下降, 直到趋近于某一固定值。这是由于轨道交通在刚进入城市客运系统时充分发挥出大运量、高速度的特点, 并且不受常规地面交通堵塞的影响, 给市民出行带来便利, 因此表现出极强的竞争力, 在初期吸引大量客源, 从而在城市公共交通的环境下生存下来, 并作为一种新兴出行方式, 在客流市场占据一定优势, 不断发展壮大。而地面公交受其冲击, 由于服务的同质性和运营能力的差距, 在短时间内客运量迅速下降, 但地面公交在长期运营中积累了稳定的人气和固定的客源, 因此它并不会迅速衰败, 其最终客运量会下降到一定水平。此时地面公交系统应该做出适当的战略调整, 如改善票价、提高发车频率、调整线路等, 提高自身竞争力, 以吸引客流。

	Figure Option View Download New Window
	图3 局部热竞争时期演化趋势Fig.3 Evolution during stage of local hot competition

(2)全面热竞争时期

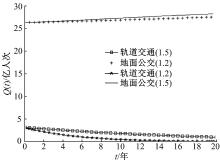
当局部热竞争持续一段时间以后, 地面公交对强势的轨道交通系统采取竞争反制策略, 双方进入全面热竞争时期。此时α _it> 1, α _ti> 1, 考虑到两种方式影响强弱程度不同, 令α _it=1.2, α _ti=1.5(即图4中地面公交(1.5)与轨道交通(1.2)的比较, 此时轨道交通竞争力度弱于地面公交); 或令α _it=1.5, α _ti=1.2(即图4中地面公交(1.2)与轨道交通(1.5)的比较, 此时轨道交通竞争力强于地面公交), 分别就两种情况进行演化趋势分析, 如图4所示。

	Figure Option View Download New Window
	图4 全面热竞争时期演化趋势Fig.4 Evolution during stage of total hot competition

从仿真结果可见:在全面热竞争时期的激烈状态下, 初始规模较大的地面公交由于长期运营积累的影响力和稳定客源在竞争中能够生存下来并且发展壮大, 而初始规模较小的轨道交通则因根基不稳, 其发展受到抑制。由于地面公交的策略调整, 竞争势头较强, 新进入城市客运市场的轨道交通企业若不调整战略, 局面会极其不利, 因此轨道交通企业在改善自身竞争力同时, 必须在竞争或合作方面调整策略来吸引客流。

3.2 冷竞争时期

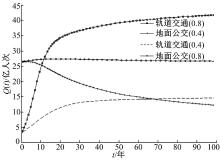
当进入冷竞争时期时, 0< α _it< 1, 0< α _ti< 1, 考虑到两种方式影响强弱程度不同, 可赋值为α _it=0.6, α _ti=0.4(即图5中地面公交(0.4)与轨道交通(0.6)的比较, 此时轨道交通竞争力度强于地面公交); 或令α _it=0.4, α _ti=0.6(即图5中地面公交(0.6)与轨道交通(0.4)的比较, 此时轨道交通竞争力度弱于地面公交), 分别就两种情况进行演化趋势分析, 如图5所示。

	Figure Option View Download New Window
	图5 冷竞争时期演化趋势分析Fig.5 Evolution during stage of cold competition

从仿真结果可见:冷竞争时期给两种方式提供了一个缓和竞争的环境, 两种方式都能够在相互磨合中生存下来, 并且能快速发展到自身最大的客流容量。在进入发展期之后, 轨道交通会逐步发展自身的路网结构, 改善运营模式, 经过一段时间, 会逐渐形成较为完善的经营策略, 提升服务质量。其扩展线路和换乘路网的形成也进一步提高了系统的可达性和便利性, 因此对客流的吸引能力会逐渐加强; 而地面公交也由于线路调整和服务能力提升, 可以为市民出行提供更加便捷的服务, 从而即使面对日益壮大的轨道交通, 也仍能在市场占据一定的稳定地位, 双方在未展开合作的前提下仍能保持共存的局面。但从长期发展的角度来看, 由于经济社会稳定发展, 人们出行需求也不断增大, 这也敦促轨道交通和地面公交提高服务水平和运营能力, 以满足人们日益增长的出行需求, 从而在城市客运市场上生存。在交通设施等资源一定的情况下, 两种方式必须进一步完成战略调整, 依照竞争演化理论, 两种城市客流系统只有相互协作, 才能满足出行需求。

3.3 热合作时期

当进入热合作时期时, 0< β _it< 1, 0< β _ti< 1, 考虑到两种方式影响强弱程度不同, 可令β _it=1.2, β _ti=1.5(即图6中地面公交(1.5)与轨道交通(1.2)的比较, 此时轨道交通合作力度弱于地面公交); 或令β _it=1.5, β _ti=1.2(即图6中地面公交(1.2)与轨道交通(1.5)的比较, 此时轨道交通合作力度强于地面公交), 在两种不同情形下分析二者的演化趋势, 如图6所示。

	Figure Option View Download New Window
	图6 热合作时期演化趋势Fig.6 Evolution during stage of hot cooperation

从仿真结果可见:双方在实施热合作策略前提下均可以顺利发展, 并日趋完善, 直到可达到各自的预期规模。这是由于随着轨道交通和地面公交在相互竞争过程中不断发展自身运营结构与服务水平, 刺激城市居民的出行的不断发展, 但双方各自的资源虽然依然在增长, 但其发展速度远远不及城市社会的发展, 在基础设施与车辆资源有限的前提下, 两种方式均无法通过单独运营满足市民日益增长的出行需求。在此情况下双方会展开合作, 通过线路的对接, 服务的衔接, 逐渐形成以轨道交通为骨干, 地面公交为支撑的公共交通出行结构, 互相补充, 相辅相成, 进而实现互利共生, 最终均可稳定发展。

3.4 冷合作时期

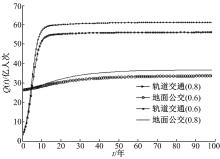
当进入冷合作时期时, 0< β _it< 1, 0< β _ti< 1, 考虑到两种方式影响强弱程度不同, 可令β _it=0.6, β _ti=0.8(即图7中地面公交(0.8)与轨道交通(0.6)的比较, 此时地面公交合作力度强于轨道交通); 或令β _it=0.8, β _ti=0.6(即图7中地面公交(0.6)与轨道交通(0.8)的比较, 此时地面公交合作力度弱于轨道交通), 分别就两种情况进行演化趋势分析, 如图7所示。

	Figure Option View Download New Window
	图7 冷合作时期演化趋势Fig.7 Evolution during stage of cold cooperation

从仿真结果可见:两种方式合作趋于平稳时, 均可顺利发展且能达到甚至超过预期规模, 进而稳定在一个更高的数值。而社会经济发展与公交条件完善会刺激居民交通出行需求增长, 若两种方式运输规模不能进一步提升, 就无法满足居民出行需求。

当交通基础设施无法进一步发展时, 两种方式必须改变自身战略, 提高自身服务能力和运营效率。由于当前竞争演化理论下冷竞争合作为最终阶段, 双方的客运市场份额已经达到均衡状态, 无法通过改变既有的合作策略取得更多客运优势。为此, 需要政府提供新的运营激励机制, 并发布新的市民出行指向政策, 优化运营结构, 运营公司协作提出新的换乘衔接模式, 并为市民出行提供信息引导等服务提高运营效率, 实现供需均衡。

上述分析表明:轨道交通和地面公交在竞争演化中互相作用及制约, 并且不断在竞争及合作中发展成熟, 提升营运能力, 采用合适营运策略, 从而在城市客运市场上生存壮大。由此可见, 竞合关系及其演化方向取决于竞争或合作力度。

4 结论

(1)轨道交通和地面公交的竞合关系演化方向的系统动力在于双方竞争或合作力度。

(2)轨道交通进入城市公交体系的初期, 双方竞合关系演化进入局部热竞争时期。面对轨道交通的强势竞争, 地面公交系统需要及时引进适当的战略调整, 提高自身竞争力, 逐步夺回客源份额。

(3)在调整营运策略后, 竞合关系演化进入全面热竞争时期。轨道交通在改善自身竞争力的同时, 必须调整竞争策略以吸引客流。

(4)在经过双方激烈竞争和相互磨合后, 竞合关系演化进入冷竞争时期。双方均能在现有的交通需求前提下快速发展到自身最大客流容量, 并在未展开合作的前提下仍能保持共存局面。

(5)经过一段时间的竞争和相互磨合, 双方营运服务能力日趋完善, 竞合关系演化进入热合作时期。双方实现互利共生及稳定发展, 客流量均可达到双方各自的预期规模。

(6)双方合作趋于平稳, 竞合关系演化进入冷合作时期时, 需政府提供新的激励机制, 整合资源, 提升城市公交整体运营效率, 实现供需均衡。

本文的研究结论在一定程度上可为城市公交系统整体规划和运营政策导向提供理论依据。但由于本文中未对自组织演化, 当地经济发展及集疏运条件、人口、土地资源等影响因素之间的关系展开深入分析, 因此受城市发展约束的增长演化及其对竞合关系的影响机制仍需要进一步研究。此外, 城市公交系统与其他城市客运营运方式的竞合关系也会是下一步研究的重点。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Tabuchi T. Bottleneck congestion and modal split[J]. Journal of Urban Economics, 1993, 34(8): 414-431. [本文引用:1]
[2]	Holland er Y, Prashker J N. The applicability of non-cooperative game theory in transport analysis[J]. Transportation, 2006, 33(5): 481-496. [本文引用:1]
[3]	刘华胜. 城市轨道交通与地面公交协调优化关键方法研究[D]. 长春: 吉林大学交通学院, 2015. Liu Hua-sheng. Study on key methods of coordinate optimization between rail and bus[D]. Changchun: College of Transportation, Jilin University, 2015. [本文引用:1]
[4]	李橘云. 基于轨道交通的常规公交线路优化对策研究[J]. 都市快轨交通, 2009(3): 10-13. Li Ju-yun. Research on the measures for optimizing bus lines based on rail transit[J]. Urban Rapid Rail Transit, 2009(3): 10-13. [本文引用:1]
[5]	唐文彬, 张飞涟, 李晶晶, 等. 城市轨道交通与常规公交的合作博弈定价模型[J]. 科技进步与对策, 2012, 29(18): 69-71. Tang Wen-bin, Zhang Fei-lian, Li Jing-jing, et al. The cooperation game pricing model for urban rail and bus[J]. Science and Technology Progress and Policy, 2012, 29(18): 69-71. [本文引用:1]
[6]	黄建中, 余波. 接驳城市轨道交通的社区公交研究——以上海市为例[J]. 城市规划学刊, 2014(3): 77-84. Huang Jian-zhong, Yu Bo. A research on integrating community bus with urban railway system: the case study of shanghai[J]. Urban Planning Forum, 2014(3): 77-84. [本文引用:1]
[7]	孙杨, 孙小年, 孔庆峰, 等. 轨道交通新线投入运营下常规公交网络优化调整方法研究[J]. 铁道学报, 2014, 36(3): 1-8. Sun Yang, Sun Xiao-nian, Kong Qing-feng, et al. Methodology of bus network optimization and adjustment under operation of new urban rail transit line[J]. Journal of the China Railway Society, 2014, 36(3): 1-8. [本文引用:1]
[8]	马天山, 曹玮, 乔新宇. 城市轨道交通与接运公交换乘优化模型[J]. 长安大学学报: 自然科学版, 2013, 33(4): 80-85. Ma Tian-shan, Cao Wei, Qiao Xin-yu. Optimization model of shuttle between urban-rail and feeder-bus[J]. Journal of Chang'an University (Natural Science Edition), 2013, 33(4): 80-85. [本文引用:1]
[9]	张杰林, 李铁柱. 基于竞争模型的轨道交通与地面公交共线分析[J]. 交通信息与安全, 2014, 32(4): 108-112. Zhang Jie-lin, Li Tie-zhu. Urban rail transit and bus collinear analysis based on competition model[J]. Journal of Transport Information and Safety, 2014, 32(4): 108-112. [本文引用:1]
[10]	Mohaymany A S, Gholami A. Multimodal feeder network design problem: ant colony optimization approach[J]. Journal of Transportation Engineering, 2010, 136(4): 323-331. [本文引用:1]
[11]	Song Li-jing, Chen Feng, Xian Kai, et al. Research on a scientific approach for bus and metro networks integration[C]//8th International Conference on Traffic and Transportation Studies, Changsha, China, 2012: 740-747. [本文引用:2]
[12]	Nand uri V, Kazemzadeh N. Economic impact assessment and operational decision making in emission and transmission constrained electricity markets[J]. Applied Energy, 2011, 96: 212-221. [本文引用:1]
[13]	Sivakumaran K, Li Y W, Cassidy M J, et al. Cost-saving properties of schedule coordination in a simple trunk-and -feeder transit system[J]. Transportation Research Part A, 2011, 46(1): 131-139. [本文引用:1]

1993

0.0

... Tabuchi^[1]分析了各种付费方式下交通方式间的竞争机制 ...

2006

0.0

... Hollander等^[2]发现促使交通方式间争夺客源的原因是各经营者追求自身收益最大化 ...

2015

0.0

... 刘华胜^[3]研究了轨道交通建成或运营时与地面公交之间相关的站点、网络优化,运营协调与突发事件应急联动等关键问题 ...

0.0

. , 2009(3):10-13 DOI:doi:10.3969/j.issn.1672-6073.2009.03.003

Research on the measures for optimizing bus lines based on rail transit

基于轨道交通的常规公交线路优化对策研究

Li Ju-yun.

李橘云

作为城市公共交通体系的两大主要方式,轨道交通与常规公交的协调发展关系到城市公共交通系统的核心竞争力。从出行时耗、出行费用、出行OD分布3个方面分析轨道交通走廊内常规公交与轨道交通的主要竞争客流范围,提出基于轨道交通的常规公交线路优化调整的6项对策,包括另行安置、走向调整、站点调整、长线截短、保留竞争、新增加密等。

... 李橘云^[4]从时间、费用和需求等角度分析了轨道交通主干线上两类公共交通方式的主要客流竞争范围,提出接驳线路优化调整对策 ...

2012

0.0

. 2012, 29(18):69-71

The cooperation game pricing model for urban rail and bus

城市轨道交通与常规公交的合作博弈定价模型

Tang Wen-bin , Zhang Fei-lian , Li Jing-jing

唐文彬, 张飞涟, 李晶晶

... 唐文彬等^[5]提出了方式间竞合理论框架,以出行时间和综合成本为目标,分析了公共交通与非机动车及私家车间的竞争关系 ...

0.0

... 黄建中等^[6]分析了上海轨道交通6号线对出行时间和费用的影响,构建了城市公交系统效用函数,分析了两种公交方式之间的竞合关系,构建了客流选择模型 ...

2014

0.0

. 2014, 36(3):1-8

Methodology of bus network optimization and adjustment under operation of new urban rail transit line

轨道交通新线投入运营下常规公交网络优化调整方法研究

Sun Yang , Sun Xiao-nian , Kong Qing-feng

孙杨, 孙小年, 孔庆峰

... 孙杨等^[7]以复杂网络为手段,研究了市内公交与其他客运方式,特别是轨道交通的竞合模式 ...

2013

0.0

. 2013, 33(4):80-85

Optimization model of shuttle between urban-rail and feeder-bus

城市轨道交通与接运公交换乘优化模型

Ma Tian-shan , Cao Wei , Qiao Xin-yu.

马天山, 曹玮, 乔新宇

不同运输方式之间是否有效接驳对城市公共交通影响甚大.针对中国城市常规公交与轨道交通之间的换乘效率的现状,进行了城市常规公交的特例——接运公交与轨道交通在城市出行平峰时段内的换乘优化研究,首先通过对换乘乘客行走时间分布的研究,建立了换乘乘客走行时间模型,进而建立乘客换乘总时间模型,模型采用接运公交在研究时段内采用不等间隔发车的方式,以接驳轨道交通列车,从而达到乘客换乘总时间最短的目的,采用了遗传算法对模型进行优化计算.计算结果表明:平峰期间接运公交不等间隔发车可以减少人均换乘时间约109.5 s,降幅为19.8％,对于2种交通方式之间有效接驳的促进作用是明显的,具有一定的实用价值；发车间隔的优化,对于乘客换乘时间的降低作用非常明显,不仅在运力资源一定的情况下改善了公共交通的服务水平,更使得2种交通方式之间的接驳得到了进一步优化,该方法具有一定的理论指导意义和实用价值.

... 马天山等^[8]分析了轨道交通与地面公交之间的换乘优化模型 ...

2014

0.0

. 2014, 32(4):108-112

Urban rail transit and bus collinear analysis based on competition model

基于竞争模型的轨道交通与地面公交共线分析

Zhang Jie-lin , Li Tie-zhu.

张杰林, 李铁柱

... 张杰林等^[9]研究了在共线的前提下,轨道交通与地面公交在经营模式和客源分配上的竞争 ...

2010

0.0

... Mohaymany等^[10]采用蚁群算法分析并优化了多方式的城市接运网络,强调了多方式的协同 ...

2012

0.0

... 1 城市公共客运系统自组织演化的假设总体而言,一般类型城市公共客运交通系统的自组织演化来自于其系统内、外竞争和自身协调等诸多方面的共同作用^[11] ...

... (4)由于影响因素对系统自组织演化的阻滞作用,系统自组织演化过程可采用Logistic方程^[11]来描述 ...

2011

0.0

... 依照微分方程稳定性理论^[12]对均衡点^[13]进行比较分析,可得两种方式竞争形态模型的均衡点和稳定性,如表1所示 ...

2011

0.0

... 依照微分方程稳定性理论^[12]对均衡点^[13]进行比较分析,可得两种方式竞争形态模型的均衡点和稳定性,如表1所示 ...