混凝土真三轴试验采用100 mm的立方体试件, 采用同一厂家生产的型号相同的新塑料磨具成型, 试块的浇筑面采用SHM-200双端面磨石机机械磨平。浇筑面与其平行面之间的平行度误差小于0.003 rad, 不同试块在浇筑面法线方向上的长度误差为± 0.6 mm。

混凝土由水泥、粗骨料、细骨料、水和消泡剂组成。其中, 水泥为中国建筑材料科学研究院监制北京兴发水泥有限公司生产的型号分别为PⅡ 42.5和PO42.5的普通硅酸盐水泥, 每种水泥各占总量的一半; 粗骨料是用北京门头沟地区出产的用反击式破碎机加工的石灰岩碎石, 最大粒径为10 mm, 颗粒呈立方体; 机制砂是以石灰岩为原材料加工而成, 最大颗粒粒径为4 mm; 细黄砂产于北京昌平地区; 细骨料用砂采用机制砂和细黄砂的混合物, 两者质量之比为1∶ 2。消泡剂是北京建筑工程研究院生产的ANX-Ⅲ 型固体消泡剂。1 m³混凝土中所含PⅡ 42.5水泥、PO42.5水泥、粗骨料、机制砂、细黄砂、水和消泡剂的质量分别为182、182、1123、229、459、225、2.4 kg。

新拌混凝土的坍落度为8 mm。在加载前, 混凝土试块的6个表面都分别涂黄甘油、贴塑料各3层, 以便消除试块与压头之间的摩擦力, 认为试块表面只受正应力作用, 不受剪应力作用。混凝土的龄期大于300 d, 选取5块试块, 测得混凝土的单轴抗压强度为38.1 MPa, 劈裂抗拉强度为5.5 MPa。

加载设备采用大连理工大学海岸和近海工程国家重点实验室的电液伺服系统试验机, 3个方向均可采用位移反馈控制和荷载反馈控制^[16]。

为了测量试块的受力和变形, 在设备的每个轴向安装一个荷载传感器和一对型号相同的LVDT位移传感器。荷载传感器出厂设计量程为2500 kN, 整个测力系统在250 kN时重复性误差小于4 kN; 每个轴向测得的荷载除以垂直于该轴向的试块截面面积就是相应轴向的正应力。位移传感器量程为20 mm, 出厂非线性度为千分之一。测量同一轴向位移的两个传感器固定在压头侧面, 关于轴线对称。二者测得量的平均值就是两个压头在该轴向的相对位移, 近似认为是试块长度的变化值。

对混凝土试块进行应力-应变混合路径下的真三轴试验。首先三个轴向等比例加载到设定值p; 然后保持Z轴向应力恒定, X轴与Y轴应变速率比α = ε·X/ ε·Y也恒定, 进行单调加载。试验中p的取值有3档(10、15和20 MPa)。α 的取值有3~4档, 分别在0.25、0.5、0.75、1.0中选取。

利用p与α 的组合来定义加载路径的代号, 例如, 应力路径的符号P10-0.5, 表示第2阶段的起点应力为10 MPa, 加载应变速率比为0.5。特别强调的是在数据分析过程中, 引入ε ’_i=ε _i-ε _{i, E}, i=X, Y, Z, ε _{i, E}为初始3个轴向等比例加载到设定值p时各轴向对应的应变。使用ε ’_i可以消除之前各轴向应变误差的影响^[10]。

按照前述的试验方法, 测得混凝土在应力-应变混合路径加载下混凝土强度的平均值如表1所示, 其中σ ₁、σ ₂、σ ₃分别为最大主应力、中主应力和最小主应力; σ _X、σ _Y、σ _Z分别为3个轴向的正应力, 约定压应力为正; f_c为混凝土的单轴抗压强度。

表2

Table 2

表2(Table 2)

表2 不同加载路径下混凝土平均强度值 Table 2 Average compressive strength of concrete under different load paths MPa 加载路程 试块数量 σ 3=σ Z σ 2=σ X σ 1=σ Y σ 1/fc σ 2/σ 1 P10-0.25 2 10.1 50.1 100.9 2.65 0.50 P10-0.5 3 9.9 68.1 98.4 2.58 0.69 P10-0.75 2 10.1 77.7 94.1 2.47 0.83 P10-1.0 2 10.1 87.3 91.2 2.39 0.96 P15-0.25 2 15.0 63.5 115.6 3.03 0.55 P15-0.5 2 15.2 82.9 113.1 2.97 0.73 P15-0.75 2 14.9 95.9 110.9 2.91 0.87 P20-0.25 2 20.2 74.7 128.1 3.36 0.58 P20-0.5 2 20.2 98.0 129.3 3.39 0.76 P20-0.75 2 20.0 112.1 126.1 3.31 0.89 P20-1.0 2 20.1 119.1 121.3 3.18 0.98

表2 不同加载路径下混凝土平均强度值 Table 2 Average compressive strength of concrete under different load paths MPa

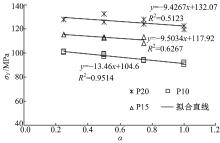
由表2和图1可知:真三轴压缩试验下混凝土强度比单轴提高很多, 并且σ ₁/f_c随着最小主应力的增大而增大; Y轴峰值强度随最小主应力的增大而增大, 这是由σ _X和σ _Z的侧向约束所致。当加载应变速率比α 为0.25时, 随着最小主应力σ _Z依次取10、15和20 MPa, 混凝土强度分别为单轴抗压强度的2.65、3.03和3.36倍; 当最小主应力σ _Z相同时, 混凝土的强度随着加载应变速率比α 和σ ₂/σ ₁的增大而递减; 当最小主应力σ _Z为20 MPa时, 随着加载应变速率比α 依次取0.25、0.5、0.75和1.0, 混凝土强度分别为单轴抗压强度的2.65、2.58, 2.47和2.39倍。特别强调的是, 试验中所有σ ₂/σ ₁≥ 0.5。姚家伟等^[17]对普通混凝土进行了应力比分别为0.1∶ 0.25∶ 1、0.1∶ 0.5∶ 1、0.1∶ 0.75∶ 1和0.1∶ 1∶ 1的常规三轴和真三轴试验, 设定受压为负。从文献[17]中的图2中可以清楚地看出:在三轴受压条件下, 当中间主应力和最大主应力比值也大于0.5时, 随着比值的增大, 混凝土的强度也是线性递减的。本文试验结果与文献[17]是一致的, 这说明加载方式不是影响混凝土强度变化的主要因素, 混凝土强度的变化与各轴向应力之间的相互作用有关。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 不同加载路径下Y轴峰值强度图Fig.1 Peak strength of Y-aixs under different load paths

应力-应变曲线是描述混凝土力学行为的重要形式, 研究目的不同, 绘制的曲线形式也不同。本试验中混凝土材料处在类似于平面应力的受力状态, 破坏机理为压应力作用下的剪切破坏, 因此分析剪应力τ ₁₃和剪应变r’₁₃之间的关系尤为重要。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 τ 13-r’13曲线图Fig.2 Curves of τ 13-r’13

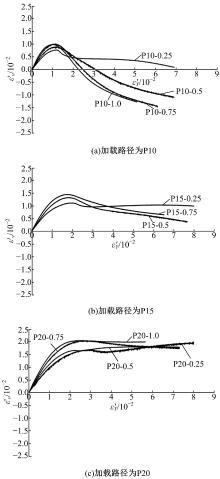
根据图2中τ ₁₃-r’₁₃曲线下降段的平缓程度, 可以将曲线分为两类:①α =0.25和α =0.5的归为Ⅰ 类, Ⅰ 类τ ₁₃-r’₁₃曲线临近加载结束时, 都逐渐变成水平直线, τ ₁₃几乎不再随r’₁₃的增加而发生变化。该阶段最终破坏面附近的混凝土已经形成了剪切带, 并且包含一定厚度的粉末, 两个破坏面已经分别贯通, 相邻楔形体块之间的内聚力损失殆尽, 几乎只剩下正压力和摩擦力。因此推断, 剪切带的摩擦因数基本不随剪切位移的增加而变化, 可以视为常数; ②α =0.75和α =1.0的归为Ⅱ 类, Ⅱ 类τ ₁₃-r’₁₃曲线在加载结束点还有下降的趋势。τ ₁₃随r’₁₃的增加而降低, 破坏面两侧的楔形体试块发生相对滑动时, 剪切带内部颗粒发生滚动和挤压, 剪切带还未完全形成。

对于所有的τ ₁₃-r’₁₃曲线, 无论最小主应力σ _Z和加载应变速率比α 取值是否分别相同, 在上升段中都有一段彼此重合的, 初始的剪切刚度相同。本试验加载的第一阶段是按各轴向应力1∶ 1∶ 1进行加载的, 这说明单调地增加静水压力不会影响混凝土的初始剪切模量。此外, 在相同加载应变速率比α 下, 最小主应力σ _Z越大, 最大剪应力和剪应变也越大。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同加载路径下的ε ’v-ε ’Y曲线Fig.3 Relationship between ε ’v and ε ’Y under different load paths

2.4.1 ε ’_v-ε ’_Y关系分析

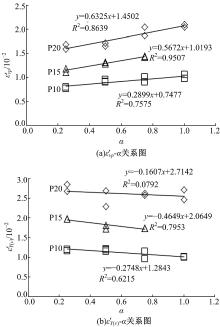
在应力-应变混合路径的加载条件下, 混凝土试块ε ’_v-ε ’_Y关系如图3所示, 其中ε ’_v=ε ’_X+ε ’_Y+ε ’_Z。加载结束时, 除了α =0.25之外, 最小主应力σ _Z=10 MPa对应的残余体积应变值都为负, 混凝土试块最终呈现体积膨胀的特性, 见图3(a); 而当最小主应力σ _Z=15 MPa和20 MPa时, 残余体积应变为正, 最终试块被压缩。此外最小主应力较小时, ε ’_v-ε ’_Y曲线在加载结束时都有继续下降的趋势, 而当最小主应力较大时, 曲线最终趋于平缓或者有上升的趋势。这主要是因为在剪切带形成的过程中和形成之后, 剪切带两侧试块发生滑动, 内部的颗粒发生偏转甚至滚动。如果正压应力较小, 剪切带发生体积膨胀; 如果正压力较大, 剪切带中颗粒被进一步碾碎, 剪切带发生压缩; 如果剪切破坏面上的正压力适中, 剪切带两侧颗粒碾碎产生的压缩与颗粒滚动引起的膨胀效应达到平衡, 剪切带的整体厚度不发生改变, 试块整体的体积近似保持恒定, 如图3(c)中曲线P20-1.0所示。

普通混凝土材料呈应变硬化软化和剪切膨胀的特性。由图3可知, 所有的ε ’_v-ε ’_Y曲线都有上升段和下降段。上升段对应加载起点到压缩体积应变的峰值点, 在该阶段混凝土中原有微裂隙在压应力作用下逐渐闭合, 试件被压密, 随着剪应力的逐渐增大, 压缩体应变逐渐增加, 当应力差到达一定阶段, 微裂缝开始扩展, 体应变的增加速率逐渐降低, 直到体积压应变到达峰值点, 该点也是扩容起点。下降段是过了峰值点之后, 微裂缝加速扩展并贯通, 试块的体积变化由压缩变为膨胀。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 峰值体积应变ε ’vp以及对应的ε ’Y(v) 随应变加载速率比α 的变化曲线Fig.4 Curves of ε ’vp-α and ε ’Y(v)-α

图4(a)给出了峰值体积应变和加载应变速率比α 的关系图。试验结果表明, 峰值体积应变ε ’_vp随着最小主应力σ _Z和应变速率比α 的增大而增大, 这是由于较大的围压限制了裂缝的产生和体积的膨胀。此外, 在相同Y轴压应变ε ’_Y下, 加载应变速率比α = ε·X/ ε·Y越大, X轴压应变ε ’_X越大。虽然ε ’_X的增加会导致混凝土试块在Z方向发生膨胀, 但是由于泊松比较小, X轴压应变的增大远大于Z轴拉应变的增大, 而ε ’_vp=ε ’_X+ε ’_Y+ε ’_Z, 最终导致峰值体积应变的增加。图4(b)则给出体积应变峰值点对应Y轴应变ε ’_Y(v)与α 之间的相互关系。试验结果表明, 当最小主应力相同时, 扩容起点随加载应变速率比的增加而减小; 当加载应变速率比相同时, 扩容起点随着最小主应力的增加而增大。由于扩容起点被认为是试块开始膨胀开裂点, 由此可见, 最小主应力的增加延迟了破坏开始的进程, 而加载应变速率比的增加则加速了破坏的进程。

2.4.2 最大主应变Y轴应力峰值点和体积应变峰值点相互关系分析

最小主应力σ _Z的取值对Y轴峰值点的位置、ε ’_v-ε ’_Y曲线峰值点的位置、以及它们峰值点的相对位置都有影响, 这里的位置是指所述点对应的ε ’_Y。将Y轴峰值点对应的ε ’_Y(即ε ’_Y(p))和ε ’_v-ε ’_Y的峰值点的对应的ε ’_Y(即ε ’_Y(v))进行对比分析, 画出ε ’_Y(p)-α 和ε ’_Y(v)-α 相互关系图, 如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
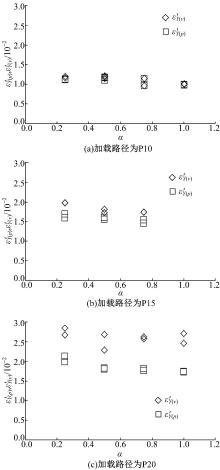	图5 Y轴应力峰值点对应的ε ’Y(p)和体积 应变峰值点对应的ε ’Y(v)对比图Fig.5 Comparison of ε ’Y(p) corresponding to peak point of Y-axis with ε ’Y(v) corresponding to peak point of ε ’v-ε ’Y

由图5可知, 加载应变速率比α 相等时, 当最小主应力σ _Z依次取为10、15、20 MPa时, 虽然Y轴应力峰值点对应的应变ε ’_Y(即ε ’_Y(p))也在依次增大, 但是ε ’_v-ε ’_Y的体积应变峰值点的对应的ε ’_Y(ε ’_Y(v))依次增加的幅度更大。从图5(a)可以看出, 当σ _Z=10 MPa时, 对于α 分别取0.25、0.5、0.75和1.0这4种情况, ε ’_Y(p)和ε ’_Y(v)相差不大, 说明Y轴应力峰值点和压缩体积应变的峰值点几乎同时出现, 该体积应变峰值点同时也是扩容起点; 当σ _Z=15 MPa或者σ _Z=20 MPa, α 依次取0.25、0.5、0.75时, 都存在ε ’_Y(p)< ε ’_Y(v)。但是σ _Z=15 MPa时, ε ’_Y(p)和ε ’_Y(v)之间相距较近, 如图5(b)所示; σ _Z=20 MPa时, ε ’_Y(p)和ε ’_Y(v)之间相距较远, 如图5(c)所示。这说明混凝土试块的扩容起点的出现滞后于Y轴应力峰值点, 并且最小主应力越大, 滞后性越明显。