竹板增强胶合木梁受弯性能

引用本文

郭楠, 张平阳, 左煜, 左宏亮. 竹板增强胶合木梁受弯性能. 吉林大学学报(工学版), 2017, 47(3): 778-788
GUO Nan, ZHANG Ping-yang, ZUO Yu, ZUO Hong-liang. Bending performance of glue-lumber beam reinforced by bamboo plyboard. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 778-788 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703013
Permissions

竹板增强胶合木梁受弯性能

郭楠¹, 张平阳¹, 左煜², 左宏亮¹

1.东北林业大学土木工程学院,哈尔滨 150040

2.哈尔滨工业大学建筑学院,哈尔滨 150006

作者简介:郭楠(1978-),男,副教授,博士.研究方向:现代木结构.E-mail:snowguonan@163.com

基金项目:中央高校基本科研业务费专项资金项目(2572015CB29); 国家留学基金委项目(201606605044)

摘要

对21根竹板增强胶合木梁的抗弯性能进行了研究,对比分析了竹板层数和厚度影响下木梁破坏形态、极限荷载和跨中挠度等参数。试验结果表明,与纯胶合木梁相比,底部粘贴1~3层胶合竹板梁的破坏荷载提高了16.8%~45.9%,随着竹板层数的增加,梁变形能力增强,但层间错动明显,致使梁的承载力不升反降;竹板总厚度不变,每层竹板厚度的减小对竹板增强胶合木梁的破坏形态无明显影响,整体变形明显,延性提高;竹板增强胶合木梁跨中截面应变符合平截面假定,破坏时梁顶达到抗压强度且有一定塑性高度,梁底达到极限拉应变。提出了竹板增强胶合木梁抗弯承载力计算公式,验证了公式的合理性,并给出了竹板最佳厚度比。

关键词: 土木工程; 竹板增强胶合木梁; 抗弯性能; 破坏形态; 承载力计算

中图分类号:TU366.3 文献标志码:A 文章编号:1671-5497(2017)03-0778-11

Bending performance of glue-lumber beam reinforced by bamboo plyboard

GUO Nan¹, ZHANG Ping-yang¹, ZUO Yu², ZUO Hong-liang¹

1.College of Civil Engineering, Northeast Forestry University, Harbin 150040, China

2.College of Architecture, Harbin Institute of Technology, Harbin 150006, China

Abstract

The bending performances of 21 bamboo plyboard enhanced glue-lumber beams were studied. Under the effects of bamboo plyboard layer number and thickness, the timber beam failure modes, ultimate load and mid-span deflection parameters were analyzed. Experimental results show that, compared to pure glue-lumber beams, the failure load of beams, with 1-3 layers of scuffing bamboo plyboard on the bottom, is increased by 16.8% ~ 45.9%. With the increase in the number of bamboo plyboard layers, the deformation capacity of the beams becomes stronger. However, the intercalated sliding becomes more obvious, which makes the bearing capacity of the beams decreases instead of increases. When the total thickness of the bamboo plyboard remains the same, the decrease in the thickness of each layer bamboo plyboard has no obvious influence on the failure modes of glue-lumber beam reinforced by bamboo plyboard. The total deformation is obvious and the ductility increases. The span-section strain of reinforced glue-lumber boards accords with the plane section assumption. The glue-lumber on the top of the beams reaches the compressive strength and has a certain plastic height when failure occurs. The scuffing-bamboo on the bottom of the beams reaches to the ultimate tensile strain. A formula to calculate the flexural capacity of the bamboo plyboard enhanced glue-lumber beams was put forward, which was verified. The optimum ratio of the thickness of the bamboo plyboard was given.

Key words: civil engineering; bamboo plyboard enhanced glue-lumber beam; bending performance; failure mode; bearing capacity calculation

Show Figures

0 引言

木结构房屋由于具有低碳环保、生态宜居和抗震性能优越等一系列优点, 是一种广受欢迎并具发展潜力的建筑形式。胶合木材料具有截面尺寸不受限制, 缺陷分散, 可用强度高, 便于利用小径材和劣质材等优点, 是现代木结构中的常用材料。作为结构中的主要水平受力构件, 普通胶合木梁受弯时, 大多发生由于梁底木材拉断而导致的脆性破坏, 木材的抗压强度没有得到充分利用。另一方面, 竹材加工技术的逐渐成熟, 尤其是胶合竹、重组竹技术的完善, 使竹材成为越来越受欢迎的建筑材料。因此, 本文提出了一种将胶合竹板置于胶合木底部的新型组合构件— — 竹板增强胶合木梁, 使胶合木受压, 胶合竹受拉, 充分利用两种材料的强度, 进而提高梁的承载力, 减小梁的截面尺寸, 实现更大的经济价值, 为木结构的推广做出贡献。

目前, 国内外学者针对胶合木梁的研究主要体现在通过各种材料对胶合木梁进行增强方面。文献[1]进行了18根FRP增强胶合木梁的受弯性能研究, 并与未增强梁作了对比分析, 其受弯极限承载力提高了18%~63%, 并基于力学模型分析, 提出受拉面层破坏和极限荷载等计算公式; 文献[2-8]分别研究了嵌入式碳纤维板、碳纤维布、玻璃纤维、玄武岩纤维及内嵌CFRP筋等材料加固木梁的受弯性能; 文献[9]通过BFRP材料增强胶合木梁的受弯试验, 检测不同层数的玄武岩纤维布和玄武岩纤维板对胶合木梁在极限承载力、抗弯刚度、延性系数提高中所产生的影响; 文献[10]用纤维材料和木材层板形成组合夹层, 制成胶合夹心梁, 对比了组合夹层数量, 放置方式对强度、抗弯刚度和破坏形态的影响; 文献[11]对配置非线性弯曲钢绞线胶合竹梁的受力进行了研究; 文献[12]研究了层板形状和尺寸对胶合竹梁的受弯和受剪性能的影响; 文献[13]进行了钢板加固、碳纤维加固及未加固的胶合木梁的对比试验。文献[14]提出了一种用短纤维增强的超高强混凝土层贴在胶合木的顶面和底面形成的组合梁, 对此梁进行了抗弯试验。综上可知, 虽然对竹板增强胶合木梁受弯性能的研究较少, 但用其他材料增强胶合木梁的研究已较为成熟, 一方面这些研究可以为本文的研究提供参考, 另一方面也可以作为本文的横向对比材料。

本文对7组, 共计21根竹板增强胶合木梁进行试验, 通过对比梁的破坏形态、极限荷载和跨中变形等参数, 研究了竹板层数和厚度对胶合木梁受弯性能的影响, 给出了最优竹板数量和厚度的建议, 并在此基础上建立竹板增强胶合木梁的受弯承载力计算公式, 便于此类构件的推广。

1 试验概况

1.1 材料性能

试验胶合木选用东北落叶松, 胶合竹选用楠竹。根据现行规定的试验方法, 对胶合木试件分别进行顺纹抗拉和抗压试验, 对有竹节和无竹节的胶合竹试件进行顺纹抗拉试验, 获得木材和竹材物理力学性能如表1所示, 表中所有数据均为平均值。

表1 木材和竹材主要性能指标 Table 1 The main performance of timber and bamboo

1.2 试件设计与分组

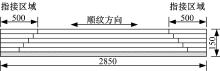
本次试验参照《木结构试验方法标准》(GB/T 50329— 2002), 《Standard Test Methods for Small Clear Specimens of Timber》(ASTM D 143)和《Standard Test Methods of Static Tests of Lumber in Structural Sizes》(ASTM D 198)进行设计, 共计21根竹板增强胶合木梁, 尺寸为2850 mm× 50 mm× 150 mm。考虑到指接对梁的强度影响较大, 应使指接位置避开纯弯段, 因此, 在加工试件时规定对于东北落叶松只允许在靠近支座两端500 mm范围内进行指接; 由于重组竹位于梁底受拉区, 指接影响更大, 因此直接选购长度超过2850 mm的胶合竹板, 来避免指接的影响, 梁的指接位置分布如图1所示。

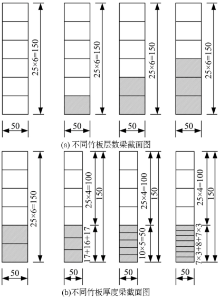
	Figure Option View Download New Window
	图1 梁的指接位置分布图(单位:mm)Fig.1 The distribution map of finger-connect position of beam

为了研究竹板层数和总数量相同时竹板厚度对胶合木梁破坏形态、极限荷载、荷载-变形等特性的影响, 按照竹板层数和厚度不同, 梁分为两组, 具体试件编号及截面组合形式如表2和图2所示。

表2 编号方案 Table 2 The numbering scheme

1.3 加载情况及测点布置

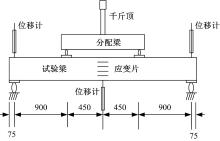
本试验采用三分点对称加载, 由16 t机械千斤顶逐级施加荷载, 并通过分配梁来进行传递。本试验所采用的梁, 高宽比较大, 为防止梁发生侧向失稳, 设计并加工了防失稳装置, 如图3所示。

加载初期, 取破坏荷载的10%~20%进行弹性加载, 先以匀速加至下限荷载, 经15~20 s匀速加至上限荷载, 随即卸载, 如此反复5次; 在破坏阶段, 以加荷速度为5~10 mm/min加载, 直至破坏, 每级加载结束稳定30 s, 进行数据采集。

在梁跨中根据层板的数量粘贴应变片, 在支座和跨中位置设位移计, 测点布置及加载示意如图4所示。试验测量内容为跨中梁表面的木纤维应变及胶合竹纤维应变、支座沉降和跨中位移, 试验数据由DH3816静态电阻应变测试仪采集。

	Figure Option View Download New Window
	图2 不同梁截面组合形式Fig.2 Section combination form of different beams

	Figure Option View Download New Window
	图3 防侧向失稳装置Fig.3 Device to prevent lateral instability

	Figure Option View Download New Window
	图4 梁加载装置及测点布置图Fig.4 Loading device and measuring points layout chart of beam

2 试验结果与分析

2.1 主要试验现象

在胶合木梁底部粘贴不同层数的胶合竹板, 进行抗弯试验, 选取每组有典型性的梁, 其破坏形态如图5所示。“ 典型” 试验梁, 即为在相同工况下最能体现胶合木梁受力情况与破坏状态的试验梁。其选定标准为:①试验梁本身无较大缺陷, 不会因木节等问题对试验结果造成较大影响; ②在同种工况下的3根试验梁中, 其极限荷载最为接近均值、挠度变化合理、试验现象明显。

本次试验共由21根试验梁组成, 限于篇幅, 无法针对每个试验梁的情况做出分析, 且非典型梁的破坏形式主要是由于胶合木梁有较大髓心木节造成的脆性破坏, 属于加工质量问题, 故不针对此种情况加以分析。

	Figure Option View Download New Window
	图5 不同竹板层数下梁破坏形态Fig.5 Failure modes of beam with different bamboo plyboard layer number

由图5可知, 纯胶合木梁发生脆性受拉破坏, 底部木板断开, 相邻层板劈裂, 且三分点处受压区出现褶皱; 底部粘贴一层竹板的胶合木梁首先在受拉边缘竹节或受压边缘木节处出现裂缝, 且在受压区顶层木板处产生褶皱, 受拉区胶合竹裂缝逐渐开展, 最终导致梁底胶合竹被拉断; 随竹板层数增加, 梁顶木材褶皱现象越发明显, 梁的变形能力加强, 最终由胶合木层板开胶和指接开裂导致破坏, 此时胶合竹板未被拉断, 其强度没有得到充分利用。

取竹板总厚度不变, 改变每层竹板的厚度, 进行抗弯试验, 选取每组有代表性的梁, 其破坏形态如图6所示。

由图6可知, 竹板总厚度相同的前提下, 每层竹板厚度的不同对胶合木梁破坏形态无明显影响, 除个别梁因缺陷问题梁底竹板被拉断外, 大多数梁均因层板开胶或在胶合木缺陷处形成水平通缝而导致破坏, 破坏时, 梁的整体变形明显, 且在梁顶三分点或跨中位置出现明显褶皱。

	Figure Option View Download New Window
	图6 不同竹板厚度下梁破坏形态Fig.6 Failure modes of beam with different bamboo plyboard thickness

2.2 极限荷载、挠度及破坏形态总结

由上述试验现象可知, 梁的破坏形态可分为梁底受拉破坏、层板开胶破坏、水平通缝破坏3种形式。梁底受拉破坏表现为梁底木板或竹板被拉断; 层板开胶破坏表现为受拉区竹板无明显破坏现象, 木板和木板之间或木板和竹板出现开胶, 最终导致破坏; 水平通缝破坏表现为在木节处形成水平通缝, 随后不断发展导致胶合木部分被完全撕裂。将表2各试验分组梁的极限荷载与破坏形态进行总结, 如表3所示。其中, 标准值为具有95%保证率的代表值, 其公式如下:

$\begin{matrix} f_{k} = μ_{f} - 1.645 σ \end{matrix}$ （1）

式中:μ _f为试件试验平均值; σ 为标准差。

表3 各试验组梁极限荷载与破坏形态 Table 3 Ultimate load and failure mode of each test group beam

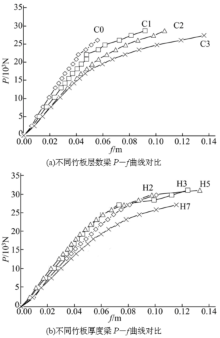
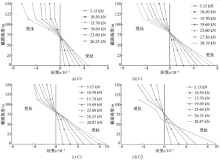
在表2所示的各试验分组中选取有代表性的一根梁, 得到其荷载-挠度(P-f)关系曲线, 如图7所示。

由表3和图7(a)可知, 纯胶合木梁的承载力最低而且变形能力最差。与纯胶合木梁相比, 粘贴一层、两层和三层胶合竹板的梁极限荷载标准值分别提高了45.9%、19.9%、16.8%, 随着粘贴层板数量的增加, 梁的变形能力越来越好, 但其极限荷载不升反降。这是因为竹板数量越多, 梁底越不容易被拉坏, 梁顶受压区塑性发展也越充分, 梁变形性能就越强, 而层板间相对错动的力也相应变大, 致使梁发生层板开胶或水平通缝破坏, 未充分利用竹材和木材的强度, 承载力降低。

	Figure Option View Download New Window
	图7 荷载-挠度曲线Fig.7 Load-deflection curves

由表3和图7(b)可知, 与普通胶合木梁相比, 竹板总厚度不变, 每层竹板厚度不同的情况下, 梁的极限荷载标准值提高了19.9%~58.7%, 随每层竹板厚度的减小, 梁的极限荷载及最终变形值均有增大的趋势, 这是因为竹板越薄, 缺陷越少; 但粘贴7层胶合竹板的H7组梁, 因胶合木部分的缺陷较大, 极限荷载较小, 破坏时跨中挠度相应减小, 不具备可比性。

2.3 荷载-应变曲线

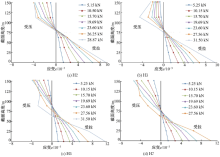
在表2所示的各试验分组中选取有代表性的一根梁, 得到其跨中荷载-应变关系曲线, 如图8、图9所示, 图中坐标轴左半部分是受压区, 应变为负, 右半部分是受拉区, 应变为正。应变片的数量和位置是根据层板的分布情况而设定, 胶合木层板中每层板的中间贴一片应变片, 胶合竹板平均每层板的中间贴一片应变片, 具体的应变片布置见图8、图9所示。

由图8可知, 在约达到极限荷载的75%以前, 各测点的应变值随荷载的增加而线性增长。

	Figure Option View Download New Window
	图8 C组典型试件荷载-应变曲线Fig.8 Load-strain curve of C group typical specimens

纯胶合木梁应变分布比较对称, 且应变值最小; 竹板增强胶合木梁的拉应变发展更为明显, 而且, 随竹板层数增加, 梁底拉应变越大; 梁顶压应变在接近极限荷载时, 随荷载增长速度放慢甚至出现了负增长, 这是由于梁顶木板受压出现褶皱所导致, 而且竹板层数越多, 这种现象越明显, 这和试验现象是吻合的。

	Figure Option View Download New Window
	图9 H组典型试件荷载-应变曲线Fig.9 Load-strain curve of H group typical specimens

由图9可知, 层板总厚度不变时, 改变层板数量, 对荷载-应变关系曲线影响不大。各梁均呈现了拉应变发展较压应变明显的特点; 随层板厚度变薄, 在加载后期, 梁顶受压区应变的突变现象略显明显, 这是因为层板厚度越小, 缺陷越少, 作为受拉部分效果也越好, 因此也越容易使梁顶木材发生受压破坏。

3 理论分析

3.1 平截面假定

在表2所示的各试验分组中选取有代表性的一根梁, 得到其跨中截面-应变关系曲线, 如图10、图11所示。

由图10、图11可知, 每级荷载下, 跨中应变沿截面高度基本呈线性分布, 接近极限时, 有个别曲线不符合此变化规律, 是因为木梁发生破坏时, 应变片被拉坏或被褶坏, 但不影响曲线整体的线性走势, 说明受弯竹板增强木梁截面应变分布符合平截面假定。

	Figure Option View Download New Window
	图10 C组典型试件截面-应变曲线Fig.10 Section-strain curve of C group typical specimens

	Figure Option View Download New Window
	图11 H组典型试件截面-应变曲线Fig.11 Section-strain curve of H group typical specimens

3.2 抗弯承载力计算公式

承载力计算推导过程中采用以下基本假定:①竹板增强木梁受弯后, 截面应变分布符合平截面假定; ②不考虑胶合面胶层厚度, 认为各层板间是一个整体; ③破坏时, 受拉区底层胶合竹板达到极限拉应变, 受压区顶部胶合木达到抗压强度, 有一定的塑性高度^[15]。

根据以上基本假定, 其等效计算简图如图12所示。

	Figure Option View Download New Window
	图12 等效计算简图Fig.12 Equivalent calculation diagram

在胶合木和胶合竹板交界处, 二者拉应变相同, 即:

$\begin{matrix} ξ_{t} = ξ_{b} (2) \end{matrix}$

由应力应变关系可知:

$ξ_{t} = \frac{f_{tu 1}}{E_{t}}$ （3）

$\begin{matrix} ξ_{b} = \frac{f_{tu 2}}{E_{b}} \end{matrix}$ （4）

由式(2)(3)(4)可得:

$\begin{matrix} f_{tu 2} = f_{tu 1} E_{b} / E_{t} \end{matrix}$ （5）

由力学平衡方程可得:

$\begin{matrix} \frac{(f_{tu} + f_{tu 2})}{2} \cdot t + f_{tu 1} \frac{h_{t} - t}{2} - f_{cu} \cdot c - f_{cu} \frac{h - h_{t} - c}{2} = 0 \end{matrix}$ (6)

由平截面假定及相似三角形关系可得:

$\begin{matrix} \frac{h_{t} - t}{h - h_{t} - c} = \frac{f_{tu 1}}{f_{cu}} \end{matrix}$ (7)

由式(6)(7)可解得:

$h_{t} = \frac{t f_{cu}^{2} + 2 h f_{cu} \cdot f_{tu 1} - t (f_{tu} + f_{tu 2}) \cdot f_{tu 1} + t f_{tu 1}^{2}}{f_{tu 1}^{2} + 2 f_{cu} \cdot f_{tu 1} + f_{cu}^{2}}$ (8)

$\begin{matrix} c = h + t \frac{f_{cu}}{f_{tu 1}} - (1 + \frac{f_{cu}}{f_{tu 1}}) \cdot \frac{t f_{cu}^{2} + 2 h f_{cu} \cdot f_{tu 1} - t (f_{tu} + f_{tu 2}) \cdot f_{tu 1} + t f_{tu 1}^{2}}{f_{tu 1}^{2} + 2 f_{cu} \cdot f_{tu 1} + f_{cu}^{2}} \end{matrix}$ (9)

根据截面静力平衡关系, 可求出梁的受弯承载力公式:

$M = b [f_{cu} \times c (h - h_{t} - \frac{c}{2}) + f_{cu} \frac{{(h - h_{t} - c)}^{2}}{3} + \frac{(f_{tu} + f_{tu 2})}{2} \times t (h_{t} - \frac{t}{2})]$ （10）

式中:ξ _t为临近胶合竹板的胶合木拉应变; ξ _b为临近胶合木板的胶合竹拉应变; E_t为胶合木抗拉弹性模量; E_b为胶合竹抗拉弹性模量; f_tu1为临近胶合竹板的胶合木拉应力, MPa; f_tu2为临近胶合木板的胶合竹拉应力, MPa; f_cu为梁顶胶合木受压时的屈服强度, 梁底边缘的极限压拉应力, MPa; f_tu为梁底边缘的极限拉应力, MPa; c为受压区塑性高度, mm; h_t为受拉区高度, mm; t为胶合竹层板厚度, mm; h为梁截面高度, mm; b为梁截面的宽度, mm。

因胶合竹层板受力不能忽略木节影响, 故在对E_b取值时, 应采用表1中竹材有木节所对应的弹性模量值。根据上述公式得到的理论值与试验值进行比较, 得到二者的误差值, 如表4所示。

由图10、图11可得, 各个工况下的构件截面-应变图均相似于图12, 即依据该等效计算简图所得出的梁受弯承载力公式, 是最具有代表性的理论公式, 且由表4可知, 梁受弯承载力计算值与试验值差值比率((计算值试验值)/试验值)大都在15%以内, 此比率在土木工程领域中属于可接受误差, 因此, 认为此梁的受弯承载力的计算公式是合理的。

通过公式可得, 在竹材厚度∶ 梁高比重=28%时, 所得跨中弯矩计算值最大, 0.28即为竹板最佳厚度比。

表4 受弯承载力理论值与试验值比较 Table 4 Comparison of theory value and test value of bending capacity

4 对比分析

本试验中采用的梁尺寸与文献[9]一致, 采用的胶合木材料分别为杨木和楠木。但通过表5、表6中L1与C1的极限承载力, 可得到两种木材的抗弯强度相似, 因此, 可对两组试验结果做对比分析。

表5 玄武岩纤维复合材料极限荷载 Table 5 Ultimate load of glue-lumber beam reinforced by basalt fiber composite material

表6 胶合竹板极限荷载 Table 6 Ultimate load of glue-lumber beam reinforced by bamboo plyboard

通过表5、表6对比可知, 玄武岩纤维材料在提高胶合木极限承载力方面的性能优于竹板增强胶合木, 且随着粘贴层数的增加, 其极限承载力提高较大。

表7给出了两组试验增强材料的基本性能, 可以得到, 玄武岩纤维复合材料的抗拉强度及受拉弹性模量远远大于竹材, 但是试验梁的极限荷载值却提高不大。说明试验中纤维材料的高强性能未充分利用, 造成材料浪费。相比之下, 竹材与木材的弹性模量相近, 在承受较大外力的情况下不易发生剥落现象, 且竹材优良的受拉性能可以得到充分利用。

表7 增强材料性能指标 Table 7 Main performance of glue-lumber beam reinforced material

5 结论

(1)底部粘贴1~3层胶合竹板的梁破坏荷载标准值比纯胶合木梁提高了16.8~45.9%。随着粘贴层板数量的增加, 梁底越不容易被拉坏, 梁的变形能力增强, 层板间相对错动也越明显, 致使梁发生层间开胶或水平通缝破坏, 梁承载力不升反降, 未充分利用竹材和木材的强度。

(2)竹板总厚度不变, 改变每层竹板厚度对胶合木梁破坏形态无明显影响, 均发生层板开胶或水平通缝破坏, 破坏时梁的整体变形明显, 随着每层竹板厚度的减小, 梁的延性越好。

(3)竹板增强胶合木梁跨中截面应变基本符合平截面假定, 受压区顶部胶合木会达到抗压强度, 并沿着截面高度有一定的塑性区域。

(4)结合平截面假定以及材料本构关系模型与力平衡条件, 推出了梁受弯承载力计算公式, 并与试验结果进行对比, 结果表明梁受弯承载理论值与试验值差值比率在15%以内, 并给出竹板最佳厚度比为0.28。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	杨会峰, 刘伟庆. FRP增强胶合木梁的受弯性能研究[J]. 建筑结构学报, 2007, 28(1): 64-71. Yang Hui-feng, Liu Wei-qing. Study on flexural behavior of FRP reinforced glulam beams[J]. Journal of Building Structures, 2007, 28(1): 64-71. [本文引用:1]
[2]	淳庆, 潘建伍, 包兆鼎. 碳-芳混杂纤维布加固木梁抗弯性能试验研究[J]. 东南大学学报: 自然科学版, 2011, 41(1): 168-173. Chun Qing, Pan Jian-wu, Bao Zhao-ding. Experiments study on bending behavior of timber beams strengthened with CFRP/AFRP hybrid FRP sheet[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(1): 168-173. [本文引用:1]
[3]	王全凤, 李飞, 陈浩军, 等. 玄武岩纤维布加固木梁抗弯性能的试验研究与有限元分析[J]. 工业建筑, 2010, 40(4): 126-130. Wang Quan-feng, Li Fei, Chen Hao-jun, et al. Experimental study on flexural behavior of timber beams reinforced with BFRP sheets[J]. Industrial Construction, 2010, 40(4): 126-130. [本文引用:1]
[4]	谢启芳, 赵鸿铁, 薛建阳, 等. 碳纤维布加固木梁抗弯性能的试验研究[J]. 工业建筑, 2007, 37(7): 104-107. Xie Qi-fang, Zhao Hong-tie, Xue Jian-yang, et al. Experimental study on behavior of timber beams strengthened with CFRP sheets[J]. Industrial Construction, 2007, 37(7): 104-107. [本文引用:1]
[5]	杨昕卉, 薛伟, 郭楠. 钢板增强胶合木梁的抗弯性能[J]. 吉林大学学报: 工学版, 2017, 47(2): 468-477. Yang Xin-hui, Xue Wei, Guo Nan. Bending performance of glued-lumber beam reinforced with steel plate[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(2): 468-477. [本文引用:1]
[6]	许清风, 朱雷, 陈建飞, 等. 粘贴钢板加固木梁试验研究[J]. 中南大学学报: 自然科学版, 2012, 43(3): 1153-1159. Xu Qing-feng, Zhu Lei, Chen Jian-fei, et al. Experiments study on behavior of timber beams strengthened with steel plates[J]. Journal of Central South University(Science and Technology), 2012, 43(3): 1153-1159. [本文引用:1]
[7]	许清风, 朱雷, 陈建飞, 等. 内嵌CFRP筋/片加固木梁受弯性能试验研究[J]. 建筑结构学报, 2012, 33(8): 149-156. Xu Qing-feng, Zhu Lei, Chen Jian-fei, et al. Experiments study on flexural behavior of strengthening timber beams with near surface mounted CFRP bars and strips[J]. Journal of Building Structures, 2012, 33(8): 149-156. [本文引用:1]
[8]	Ribeiro Alfredo S, de Jesus Abílio M P, Lima António M, et al. Study of strengthening solutions for glued-laminated wood beams of maritime pine wood[J]. Construction and Building Materials, 2009, 23(8): 2738-2745. [本文引用:1]
[9]	左宏亮, 卜大伟, 郭楠, 等. 玄武岩纤维复合材料对胶合木梁受弯性能的影响[J]. 东北林业大学学报, 2015, 43(4): 91-95. Zuo Hong-liang, Bu Da-wei, Guo Nan, et al. Effect of basalt fiber composite on flexural behavior of glulam beams[J]. Journal of Northeast Forestry University, 2015, 43(4): 91-95. [本文引用:1]
[10]	Manalo A C, Aravinthan T, Karunasena W. Flexural behaviour of glue-laminated fibre composite sand wich beams[J]. Composite Structures, 2010, 92(11): 2703-2711. [本文引用:1]
[11]	Huang Dong-sheng, Zhou Ai-ping, Bian Yu-ling. Experimental and analytical study on the nonlinear bending of parallel strand bamboo beams[J]. Construction and Building Materials, 2013, 44: 585-592. [本文引用:1]
[12]	Mujiman, Henricus Priyosulistyo, Djoko Sulistyo, et al. Influence of shape and dimensions of lamina on shear and bending strength of vertically glue laminated bamboo beam[J]. Procedia Engineering, 2014, 95: 22-30. [本文引用:1]
[13]	Issa Camille A, Kmeid Ziad. Advanced wood engineering: glulam beams[J]. Original Research Article Construction and Building Materials, 2005, 19(2): 99-106. [本文引用:1]
[14]	Toratti Tomi, Schnabl Simon, Turk Goran. Reliability analysis of a glulam beam[J]. Original Research Article Structural Safety, 2007, 29(4): 279-293. [本文引用:1]
[15]	Joints with carbon fiber-reinforced polymer rods[J]. Journal of Composites for Construction, 2005, 9(4): 337-347. [本文引用:1]

2007

0.0

. 2007, 28(1):64-71 DOI:doi:10.3321/j.issn:1000-6869.2007.01.010

Study on flexural behavior of FRP reinforced glulam beams

FRP增强胶合木梁的受弯性能研究

Yang Hui-feng , Liu Wei-qing.

杨会峰, 刘伟庆

A detail study on flexural behavior of FRP(fiber reinforced plastics/polymer) reinforced glued laminated timber(glulam) beams is presented in this paper.Through the experimental work,the failure modes and failure mechanism were discussed,then the ultimate load and the flexural stiffness of FRP reinforced glulam beams were compared with those of unreinforced control beams.It is shown that reinforced poplar glulam beams with FRP increased the ultimate load by 18%～63%,and bending stiffness by 32%～88%.And when compared with the sawn pine beams,the ultimate load and the stiffness of the reinforced poplar glulam beams with reinforcement ratio of 1.0% were 1.82 and 1.35 times higher,respectively.Furthermore,the failure modes of the reinforced beams showed ductile compression failures.Based on the analysis of mechanic model,it developed the equations for computing the interfacial bonding shear stress,position of neutral axis,tensile force in FRP strips,the load at bumper-lam failure and the ultimate load.Compared with a large number of test data,the presented model shows a satisfied accuracy and it can be used to predict the flexural behavior of FRP reinforced glulam beams.And the whole work can be taken as a reference for manufacture,design and application of this kind of structural members.

对FRP(fiber reinforced plastics/polymer)增强胶合木梁的受弯性能做了详细研究。通过试验分析了构件的破坏形态与破坏机理,对比分析了FRP增强胶合木梁与未增强梁的极限荷载与抗弯刚度等受弯性能。试验结果表明FRP增强杨木胶合木梁相对于未增强梁,受弯极限承载力提高了18%~63%,刚度提高了32%~88%,当配筋率为1.0%左右时,FRP增强杨木胶合木梁的受弯承载力与刚度分别可达到常用松木实木构件的1.82倍和1.35倍,并且增强构件的破坏形式大多表现为塑性受压破坏。基于力学模型分析,提出了粘结界面粘结剪应力、截面中性轴位置、FRP板拉力、受拉面层破坏荷载和极限荷载等的计算公式;然后将理论分析结果与现有的大量试验结果进行了对比,结果表明,模型精度较高,能够较好地预测FRP增强胶合木梁的受弯性能,可为此类结构构件的加工设计与工程应用提供参考。

2011

0.0

. 2011, 41(1):168-173

Experiments study on bending behavior of timber beams strengthened with CFRP/AFRP hybrid FRP sheet

碳-芳混杂纤维布加固木梁抗弯性能试验研究

Chun Qing , Pan Jian-wu , Bao Zhao-ding.

淳庆, 潘建伍, 包兆鼎

2010

0.0

. 2010, 40(4):126-130 DOI:doi:10.13204/j.gyjz201004027

Experimental study on flexural behavior of timber beams reinforced with BFRP sheets

玄武岩纤维布加固木梁抗弯性能的试验研究与有限元分析

Wang Quan-feng , Li Fei , Chen Hao-jun

王全凤, 李飞, 陈浩军

玄武岩纤维布是一种性能优异的新型复合材料.通过对12根矩形截面木梁的静力试验,进行玄武岩纤维布(BFRP)加固木梁抗弯性能的试验研究,分析对比梁与加固梁的承载力、挠度等结构性能指标.试验结果表明:在木梁受拉区粘贴玄武岩纤维布是提高木梁抗弯性能的有效方法.并应用ANSYS软件对BFRP布加固木梁的抗弯性能试验的全过程进行了数值模拟,得到加固木梁在竖向荷载作用下的荷载-位移曲线,应力-应变云图等.通过数值计算结果与试验结果的对比,验证了应用ANSYS程序对FRP加固木梁进行数值模拟的可行性.

2007

0.0

2017

0.0

. 2017, 47(2):468-477

Bending performance of glued-lumber beam reinforced with steel plate

钢板增强胶合木梁的抗弯性能

Yang Xin-hui , Xue Wei , Guo Nan.

杨昕卉, 薛伟, 郭楠

为了改善普通胶合木梁的受力性能,提出了在其底部粘贴钢板或增设螺钉的增强方式,从而形成钢板增强胶合木梁。进行了21根梁的抗弯试验,分析了钢板厚度、是否设置螺钉对梁破坏形态、承载力和变形能力的影响,并与普通胶合木梁进行对比。结果表明:粘贴2、3和4 mm厚钢板增强后,梁承载力分别提高了73.3%、90.0%和71.0%,随着钢板厚度的增加,承载力先增大后减小;粘贴同厚度钢板并设置螺钉后,梁承载力分别提高了76.4%、96.9%和148.6%,随着钢板厚度的增加,承载力增大,螺钉的增强效果在钢板较厚时表现明显。钢板增强后,梁的极限变形比普通胶合木梁提高了6.2%~61.1%,钢板厚度和是否设置螺钉对梁变形能力的影响与其对承载力的影响类似。在验证了钢板增强胶合木梁基本符合平截面假定后,提出了此类构件的受弯承载力计算公式,并与试验结果进行对比,结果表明,理论值与试验值的平均误差不大于10%。

2012

0.0

. 2012, 43(3):1153-1159

Experiments study on behavior of timber beams strengthened with steel plates

粘贴钢板加固木梁试验研究

Xu Qing-feng , Zhu Lei , Chen Jian-fei

许清风, 朱雷, 陈建飞

2012

0.0

. 2012, 33(8):149-156

Experiments study on flexural behavior of strengthening timber beams with near surface mounted CFRP bars and strips

内嵌CFRP筋/片加固木梁受弯性能试验研究

Xu Qing-feng , Zhu Lei , Chen Jian-fei

许清风, 朱雷, 陈建飞

2009

0.0

2015

0.0

. 2015, 43(4):91-95

Effect of basalt fiber composite on flexural behavior of glulam beams

玄武岩纤维复合材料对胶合木梁受弯性能的影响

Zuo Hong-liang , Bu Da-wei , Guo Nan

左宏亮, 卜大伟, 郭楠

摘　要：在普通胶合木梁上粘贴玄武岩纤维复合材料,经抗弯试验,检测不同层数玄武岩纤维布和玄武岩纤维板对胶合木梁的增强效果。结果表明：玄武岩纤维复合材料对胶合木梁受弯性能有很好的增强效果;与未增强的胶合木梁相比,受弯极限承载力提高幅度为20.88%~111.25%,抗弯刚度提高幅度为18.7%~27.6%,延性系数提高幅度为23.0%~74.3%。对于玄武岩纤维复合材料配量适中的增强胶合木梁,在受拉区层板破坏的同时,受压区层板出现压屈褶皱,木材抗压强度得到比较充分的发挥,破坏时表现出明显的塑性破坏特征。玄武岩纤维复合材料的存在,能有效降低木材缺陷对胶合木梁受弯性能的不良影响。

2010

0.0

2013

0.0

2014

0.0

2005

0.0

2007

0.0

2005

0.0

... ③破坏时,受拉区底层胶合竹板达到极限拉应变,受压区顶部胶合木达到抗压强度,有一定的塑性高度^[15] ...