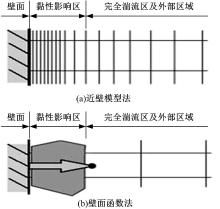
近壁模型法在黏性影响区用低雷诺数湍流模型求解; 在湍流核心区及外部区域用高雷诺数湍流模型求解; 两层之间用混合函数过渡^[17]。壁面函数法越过黏性影响区域, 通过壁面函数给布置在完全湍流区的壁面相邻单元中心点直接赋值, 壁面相邻单元之外的区域则应用高雷诺数湍流模型进行求解。

如图1所示, 处理方法的区别决定了它们对近壁网格的要求是不同的。近壁模型法要求在黏性影响区划分细密的网格以捕捉该区域的细节变化。而壁面函数法的近壁网格中心点原则上要布置在对数区内。在实际应用中, 使所有的近壁网格都布置在对数区是十分困难的。如果有近壁网格落入黏性影响区域, 势必使准确度受损。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 近壁模型法和壁面函数法Fig.1 Near-wall model approach and wall function approach

标准壁面函数^[18]基于局部平衡假设推导得到, 即假定在边界层内湍动能的生成和消散处于平衡, 并未将压力梯度对近壁流动的影响考虑在内, 因而对非平衡复杂流动中壁面摩擦和对流换热的预测会有偏差。

壁面函数通常用以下3种无量纲参数表示:

y+≡ρuτy/μ(1)

U+≡Uuτ(2)

T+≡(TW-T)ρcpuτ/q·(3)

式中:y⁺、U⁺和T⁺分别为一点到壁面的无量纲距离及该点的速度和温度无量纲参数; u_τ ≡ τw/ρ为壁面摩擦速度, τ _w为壁面切应力; ρ 为密度; y为该点到壁面的距离; μ 为动力黏度; U为该点的平均流速; T_w和T分别为壁面上的温度和该点的温度; c_p为比热容; q·为壁面热通量。

SWF由经典的层流线性律和湍流对数律简单连接而成, 壁面相邻单元中心点的速度和温度参数通过式(4)(5)计算得到:

U+=Ulam+=y+, y+< yV+Uturb+=1κlnEy+, y+≥yV+(4)

T+=Tlam+=Pry+, y+< yT+Tturb+=Prt1κlnEy++P, y+≥yT+(5)

式中:下标lam和turb分别表示层流和湍流; yV+和 yT+分别为y⁺遵循速度对数律和温度对数律的取值下限; κ 为Von Karman常数; E为常数, 取9.793; Pr和Pr_t分别为分子Prandtl数和湍流Prandtl数; P是有关Pr和Pr_t的函数。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 近壁区分层示意图Fig.2 Diagram of subdivisions of near-wall region

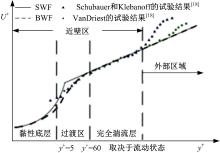
图2为近壁区分层示意图。大量试验^[19]表明, 近壁区域大体上可以分为3层。SWF也在图中标出, 在对数坐标系中, SWF的线性律部分用曲线表示, 对数律部分用直线表示。由于SWF对线性律和对数律并没有任何过渡处理, 因而图中SWF的曲线部分和直线部分存在折点。如果近壁网格中心点布置在折点所在的过渡区, SWF会给出偏高的U⁺值。根据式(2), 这将导致壁面切应力的预测偏低。而壁面切应力正是流动阻力的主要来源, 因而推测, SWF对散热器压降预测偏低的主要原因是由于近壁网格中心点落入过渡区。温差预测偏低的原因同理可推。下文将对该推测进行验证。

针对SWF对线性律和对数律的不良过渡, 采用Kader^[8]建议的方法将两种壁面律混合:

U+=eΓUlam++e1ΓUturb+(6)

T+=eΓTlam++e1ΓTturb+(7)

式中:Γ 为混合系数, 在速度壁面律中为关于y⁺的函数, 在温度壁面律中为关于Pr和y⁺的函数。

混合处理后的壁面函数(BWF)同样在图2中标出, 其在过渡区过渡平滑, 与试验数据更加吻合。

根据White和Cristoph的方法^[20], 在经典壁面律中引入压力梯度影响系数, 得到考虑压力梯度影响的壁面律。改进后的速度湍流壁面律有如下形式:

dUturb+dy+=S'κy+(8)

S'=1+αy+, y+< ys+1+αys+, y+≥ys+（9）

式中: ys+为对数斜率开始保持不变的位置; α 为压力梯度的影响系数, 定义为:

α≡μρ2uτ3dpdx(10)

改进后的速度层流壁面律写为:

dUlam+dy+=1+αy+(11)

当α 等于零时, 式(8)和式(11)代表经典的湍流壁面律和层流壁面律。改进的温度壁面律与速度壁面律的形式类似, 参见文献[20], 本文不再赘述。

用改进后的壁面律替换BWF中经典的壁面律, 可以得到改进的混合型壁面函数(IBWF)。IBWF考虑了压力梯度对近壁流动的影响, 同时在过渡区的性能也得到增强, 在理论上是适用于发动机散热器内的特定流动的。下文将分别应用SWF、BWF、IBWF与近壁模型法进行散热器数值模拟, 并通过试验对数值模拟结果进行验证, 以评估IBWF及其他近壁处理方法在散热器数值模拟中的适用性。

数值模拟在一款工程机械用波纹带散热器上进行。受限于发动机舱的布置条件, 工程机械用散热器普遍厚度较大, 空气流动通道更长, 因而其性能预测结果受近壁处理方法的影响也更为明显。

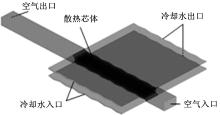
如图3所示, 简化后的计算区域分为固体区域、空气流域和冷却水流域。流域进出口均适当延长, 空气和冷却水分别以均匀分布的速度和温度从相应入口进入流域, 与固体区域交换热量。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 计算区域Fig.3 Calculation regions

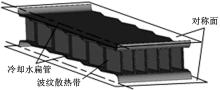
图4为波纹散热带和冷却水扁管组成的固体区域, 除了空气流动方向之外, 其他方向仅取实际散热芯体的部分周期。冷却水扁管中间面设为对称面, 从而使模型在高度上无限延伸。空气流域在宽度上包含3个散热带周期, 取中间周期作为空气侧输出结果区域。入口迎面风速在5~15 m/s内取9个风速点; 进风温度为290 K; 冷却水流速为0.18 m/s; 冷却水入口温度为345 K。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 固体区域Fig.4 Solid region

经过估算, 为了满足壁面函数法的需求, 近壁网格尺寸需要大于1.7 mm才能保证所有工况下的近壁网格均落入对数区内。然而这个值远大于满足网格无关性的网格尺寸, 如果勉强将近壁网格布置在1.7 mm以上会直接影响网格无关解的获得。因而本模型中大多数的近壁网格不得不分布在黏性影响区内。这种矛盾是由散热器内的低雷诺数流态所决定的, 是发动机散热器数值模拟中存在的典型问题。为壁面函数法模型所划分的较粗疏网格如图5(a)所示。

为了满足近壁模型法的需求划分了另一套较细密的网格, 如图5(b)所示。两套网格都采用六面体结构化网格划分。近壁模型法网格总数约为3023万; 与之相比, 壁面函数法网格总数仅为105万, 减少了96.5%, 这对计算时间和计算资源的节省是非常显著的。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 近壁区的网格划分Fig.5 Meshes of near-wall region

模拟计算在基于控制体积法的CFD软件Fluent中进行, 采用SIMPLE算法对稳态RANS方程进行求解计算。近壁区分别应用SWF、BWF、IBWF和近壁模型法进行处理, 外部区域采用可实现k-ε 湍流模型求解。

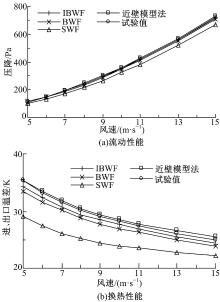
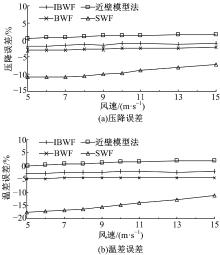
图6为散热器流动和换热性能曲线。图7为散热器性能模拟结果的压降和温差误差曲线。从图7可以看出, 近壁模型法获得的压降和温差的最大误差分别为1.6%和2.0%, 是这几种近壁处理方法中准确度最高的。而SWF误差最严重, 这两个值分别达到了-10.9%和-17.5%, 预测显著偏低。这种偏低预测在文献[7]、[22]和[23]中也有类似的报告。BWF获得的压降和温差的最大误差分别为-3.0%和-4.8%, 与SWF相比准确度有显著提高, 说明壁面函数过渡区性能的改善对散热器性能预测准确度提升具有显著效果。IBWF将最大误差进一步缩小为-1.8%和-3.0%, 显示出与试验数据非常好的一致性, 说明考虑压力梯度影响所做的改进确实使散热器性能预测准确度得到了提升。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 散热器性能的仿真和试验结果Fig.6 Simulation and test results of radiator performance

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 散热器性能的仿真结果误差Fig.7 Deviation of radiator performance simulation results

另外可以发现, SWF的准确性随风速增大有明显改善, 而BWF和IBWF并不具备这种特点。相反, 近壁模型法的误差随风速的增大反而有微小的增大。不同近壁处理方法对风速的敏感性不同可以通过考查模型的y⁺值给出解释。

SWF的准确性对y⁺是敏感的。如图2所示, 其在折点处偏差最大, 随着y⁺增大偏差逐渐缩小, 对压降和温差的偏低预测随之得到改善。而根据y⁺的定义^[11], y⁺又与流速成正相关。图8为壁面函数法近壁网格的y⁺频率分布直方图。在5 m/s时, 大部分近壁网格的y⁺值集中在10~20内, 该范围正是SWF偏差最明显的区域。随着风速的增加, y⁺值增大, 偏差逐渐缩小。因而可以说, SWF对风速敏感的根本原因是其对y⁺的敏感性。

图8

Fig.8

	Figure Option ViewDownloadNew Window
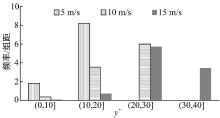	图8 不同风速下壁面函数法的近壁网格 y+频率分布Fig.8 y+ frequency distribution of near-wall meshes for different air velocity

由于BWF和IBWF在过渡区的性能得到了改善, 它们的准确度对y⁺值并不像SWF那么敏感。至于近壁模型法的误差随着风速的增大反而有微小的增大, 这是由于风速增大使网格相对于y⁺值而言变得稀疏, 但经过网格无关性验证后这一点对于结果的影响较小。

全面评估IBWF在散热器数值模拟中的适用性, 不仅需要考查其准确度, 还需要考查它所耗费的计算资源和求解时间是否经济。表1列出了文中模型采用不同近壁处理方法所需的计算资源和求解时间。

表1

Table 1

表1(Table 1)

表1 计算资源和求解时间 Table 1 Computing resources and solving time 近壁处理方法 内存/GB 处理器 求解时间/min IBWF 1.3 3.20 GHz× 1 20~30 BWF 1.1 3.20 GHz× 1 20~30 SWF 1.0 3.20 GHz× 1 60~80 近壁模型 29.0 3.20 GHz× 6 300~400

表1 计算资源和求解时间 Table 1 Computing resources and solving time

计算运行所需内存主要取决于网格的数量和计算的复杂程度。IBWF作为壁面函数法的一种, 不需要在近壁区划分细密的网格, 因而计算所需内存仅为近壁模型法的4.5%。

在求解过程中, 壁面函数法模型在个人计算机上采用单处理器串行计算; 而近壁模型法模型的求解无法在个人计算机上进行, 必须采用多处理器并行计算。尽管并行计算在计算效率上有明显优势, 然而壁面函数法所耗费的求解时间仍远远小于近壁模型法。此外, IBWF和BWF在SWF的基础上进一步节省了一半以上的求解时间。这是由于混合处理后的过渡区更加平滑, 因而计算的稳定性和收敛性都比SWF更好一些。