引用本文
刘宇, 李鹏飞, 张义民. 紫铜薄壁零件微铣加工变形分析及预测. 吉林大学学报(工学版), 2017, 47(3): 844-849
LIU Yu, LI Peng-fei, ZHANG Yi-min. Analysis and prediction of micro milling deformation of copper thin-wall parts. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 844-849  
Doi:10.13229/j.cnki.jdxbgxb201703021
Permissions
Copyright©2017, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
紫铜薄壁零件微铣加工变形分析及预测
刘宇, 李鹏飞, 张义民
东北大学 机械工程与自动化学院,沈阳 110819
张义民(1958-),男,教授,博士生导师.研究方向:机械可靠性设计,机械动态设计.E-mail:zhangymneu@sohu.com

作者简介:刘宇(1980-),男,副教授,博士.研究方向:机械结构与系统动力学.E-mail:yuliu@me.neu.edu.cn

基金项目:国家自然科学基金项目(51105067); 中央高校基本科研业务费专项资金项目(N120403011)
摘要

针对紫铜薄壁微铣削加工过程中的位移变形问题,建立了铣削力数学模型,采用四边形薄板单元有限元方法对薄壁铣削的位移变形进行分析预测。为了验证铣削力模型和薄壁变形预测的准确性,利用金刚石微铣刀对紫铜进行铣削试验。最后,通过光学显微镜和扫描电镜进行观测。结果表明:本文试验结果与仿真结果几乎吻合,证明本文建立的铣削力模型及采用的薄板变形分析方式可以有效地预测加工变形,且载荷位置与薄壁变形关系密切,切削变形随薄壁厚度的减小而快速增大。

关键词: 机械设计; 切削变形; 有限单元法; 薄壁; 微铣削
中图分类号:TH12 文献标志码:A 文章编号:1671-5497(2017)03-0844-06
Analysis and prediction of micro milling deformation of copper thin-wall parts
LIU Yu, LI Peng-fei, ZHANG Yi-min
School of Mechanical Engineering and Automation, Northeastern University, Shenyang 110819, China
Abstract

According to the deformation of copper thin-wall part in micro milling, a mathematical model of the milling force was established. The method of quadrilateral thin plate element FEM was used to predict the deformation caused by the cutting force. Experiments with diamond coated cutters were carried out to the validate the feasibility of the model and the precision of the deformation prediction. Optical Microscope (OM) and Scanning Electron Microscope (SEM) were used to observe the milled surface. Results show that the proposed mathematical model and analysis method can effectively predict the milling deformation of copper thin-wall parts. There is a close relationship between the load position and the thin-wall deformation. The cutting deformation increases quickly with the decrease in the thickness of the thin wall.

Key words: machanical design; cutting deformation; finite element method(FEM); thin-wall; micro milling
0 引言

微小薄壁指的是厚度在100 μ m以下, 高厚比大于10的悬臂结构或工字结构件。目前, 微小薄壁已经大量应用在微型燃料电池、芯片上的微通道总线、电火花加工电极等方面, 为满足这些微小零件的复杂结构特征, 需要进一步对微小薄壁结构的铣削加工技术进行研究[1]。针对传统薄壁零件的加工问题, 部分学者已进行了试验研究。Li等[2]采用有限元分析的方法对薄壁铣削过程进行研究, 分析了预测模型中参数和切削力之间的关系。Annoni等[3]研究了薄壁厚度对加工精度的影响, 并对0.4%碳钢材料进行了铣削方式和刀具轨迹的对比加工试验。戴美玲等[4]建立了非接触的光学测量试验系统, 研究了薄壁球壳受刚性平面压缩的连续变形及失稳行为。Budak等[5]建立了高性能的铣削模型, 分析了切削力、工件变形与公差的关系。Tang等[6]采用有限元仿真的方法对静态力所导致的变形进行了研究。Gang等[7]采用有限元仿真了螺旋立铣刀铣削悬臂钛合金板的过程, 获取了薄板的变形及表面误差, 并在相同条件下进行了试验验证。郭魂等[8]针对飞机型腔薄壁件刚性差的问题, 采用三维有限元法, 对航空框类零件的加工变形进行分析计算, 得到其加工变形规律。Loehe等[9]对加工过程的变形提出了较为精确的测量方法。

为了进一步对薄壁加工进行探究, Friedrich等[10, 11]通过铣削有机玻璃加工出厚8 μ m, 高62 μ m的薄壁。Bang等[12]成功铣削出了25 μ m× 650 μ m的黄铜薄壁结构。Chern等[13]也加工出了高60 μ m, 厚度分别为5、31、80 μ m的3种薄壁结构。

尽管针对传统薄壁加工已经有较多的研究, 但是针对微小薄壁加工的研究却很少。本文针对紫铜材料, 通过有限元的方法进行仿真分析, 对比了不同厚度及不同载荷位置的薄壁变形。最后通过加工试验对本文方法进行了验证。

1 薄壁加工变形机理
1.1 微铣薄壁切削力建模

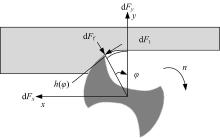
在微铣削薄壁件时, 产生的切削力会对工件造成一定的变形, 主要考虑y向的变形。采用的切削力预测模型如图1所示, 其中, n为刀具转速。

图1 铣削力模型Fig.1 Cutting force model

切削刃处的切向力dFt和径向力dFf与切削深度的关系可表示为:

dFt(φ)=Kth(φ)dzdFf(φ)=Kfh(φ)dz（1）

式中:φ ∈ (φ st, φ ex)为刀具的瞬时切削角度, φ st为切削进入角; φ ex为切削切出角, 当刀具切出时, 切削力为0; Kt为切向切削力系数; Kf为径向切削力系数; h(φ )为切削角为φ 时的切削厚度; dz为轴向切削深度, 离散后的轴向切削深度dz可表示为:

dz=d·dφ2tan(γ)（2）

式中:d为刀具的直径; γ 为刀具的螺旋角。

由文献[14]可得到铣削铜时切削力系数与刀刃半径和切削厚度的非线性关系, 具体试验中刀刃半径r为6 μ m。切向切削力系数及径向切削力系数可分别表示为:

Kt(h, r)=αthdt+βthptrqt（3）

Kf(h, r)=αfhdf+βfhpfrqf（4）

其中, 相关切削力系数的取值如表1所示。

表1 相关切削力系数取值 Table 1 Values of cutting force coefficient

切削厚度h(φ )可表示为:

h(φ)=ft·sin(φ)（5）

式中:ft为每刃每转的进给速度。

把切削力转换到x、y方向上可表示为:

Fx=Ftsin(φ)-Ffcos(φ)Fy=Ftcos(φ)+Ffsin(φ)（6）

1.2 薄壁结构切削变形分析

(1)薄板模型建立

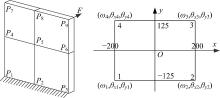
本模型将薄板划分为4个单元, 假定单元的形状及材料参数均相同, 各单元的刚度矩阵相同, 这里任取出一个400 μ m× 250 μ m的四边形单元进行分析。相应的坐标如图2所示。由图2可见, 每个节点有3个自由度, 因此4节点单元共有12个自由度。当铣削薄壁径向浸入比较小时, 任一时刻切削刃接触的长度极小, 在此模型中将切削过程中z向分力简化为点力。

图2 平板单元的局部坐标示意图Fig.2 Local coordinates sketch map of plate element

图2中, ω 为薄板在z方向上的位移; θ x为ω 对x轴的旋转角, 且有θ x=∂ω /∂y; θ y为ω 对y轴的旋转角, 且有θ x=-z∂ω /∂x。

(2)单元的刚度矩阵

4节点平板单元共有12个自由度, 刚度矩阵是一个12× 12的方阵。板单元的应变矩阵是一个3× 12的矩阵。

B=-z∂2∂x2∂2∂y22∂2∂x∂yN（7）

式中:B为单元的应变矩阵; N为单元的形函数; z为薄板的厚度。

单元刚度矩阵K的求解式为:

K=∫BTDBz2dV=∫∫-h/2h/2BTDBz2dzdA（8）

式中:D为材料的弹性矩阵。

(3)单元刚度矩阵的组集

矩形板整体共有9个节点, 可得出薄壁刚度矩阵维数为27× 27。采用矩阵转换法, 参考节点编号, 可得各单元转换矩阵G1, G2, G3, G4。其中, 各转换矩阵均为12× 27的矩阵。则薄板整体总刚度矩阵为:

K=∑i=14GTiKiGi, i=1, 2, 3, 4（9）

式中:Ki为单元刚度矩阵。

(4)静力学求解方程式

模型中各节点力的矩阵为F27× 1, 节点位移列阵为δ 27× 1, 因此, 总的静力学求解方程式是一个27维的线性方程组:

F27×1=K27×27δ27×1（10）

(5)引入边界条件并进行求解

如图2所示, 节点P1、P2、P3为固定约束, 即位移边界条件, 相应的位移及转角值为0, 由此修改总刚度矩阵, 取总刚度矩阵10~27行和10~27列组成新的总刚度矩阵为K'18× 18, 新的节点位移阵列为δ '18× 18。引入力边界条件, 在节点P9处沿z方向作用有Fz=0.235 N的集中力, 对应于节点力列阵的第25个元素, 即F(25)=0.235 N。按位移边界条件修改节点力列阵, 取节点力列阵的第10~27个元素, 形成新的节点力列阵F'18× 1。在F'18× 1列阵中, 只有第16个元素值为0.235 N, 其他元素值皆为0(因为节点P4~P9中, 只有P9处作用有外力)。

因此, 形成新的静力学平衡方程, 如下所示:

F'18×1=K'18×18δ'18×1（11）

具体求解式为:

δ'18×1=(K'18×18)-1F'18×1（12）

经Matlab计算得节点P4~P9的位移。

2 试验设备及材料
2.1 试验及检测设备

在实验室自行设计的MMT-50X微小铣床(见图3)上进行试验, 其中THK公司生产的AX1015P4AE运动平台, 配备东方电机基本步距角为0.72° 的PK566AW, 通过10细分实现x向和y向的运动, z轴配备雷尼绍RGH24Y光栅尺, 分辨率为0.1 μ m。经过激光传感器测试验证, x、y、z三个方向的运动精度、重复定位精度都在亚微米级别。主轴采用TDK65-1.2F-24K风冷电主轴。试验后通过配备的500万像素的SK2700U光学显微镜和扫描电镜进行三维轮廓的检测。扫描电镜的最大放大倍数可达100万倍以上。

图3 MMT-50X微铣床Fig.3 MMT-50X micro milling machine

2.2 试验用微铣刀具及材料选择

金刚石涂层刀具具有导热率高、摩擦因数小、热膨胀系数低、能够产生极薄的切屑、切屑容易排出、与其他物质的亲和力较小和加工中不容易产生积屑瘤等优点[15]。本试验采用瑞士MIKK金刚石涂层刀具, 刃径为0.5 mm; 刀刃半径为6 μ m; 刃数为2; 刃长为2 mm; 柄径为4 mm; 螺旋角为30° ; 颗粒度为0.02 μ m; 刀刃半径约为6 μ m。材料为紫铜, 试样尺寸为20 mm× 10 mm× 3 mm, 材料性质如表2所示。

表2 材料属性 Table 2 Properties of materials
3 结果及讨论

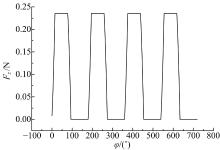
图4为主轴转速为15 000 r/min、进给速度为0.5 mm/s、径向切深为20 μ m时计算分析得到的铣削力。

图4 指定加工条件的切削力Fig.4 Cutting force of specified processing conditions

当把铣削过程中产生的切削力转化为薄板变形分析的载荷时, 主要分析垂直于加工面的载荷施加在薄壁中部和边缘时的状况。在这两种情况下, 薄壁最大的变形与载荷大小的关系如图5所示。从图5可以看出, 载荷施加在边缘时所产生的最大变形比载荷施加在中部时变形增大约90%, 这主要是因为试验所用的薄壁结构在边缘部分的刚性比中间部分差, 施加相同大小的载荷时, 变形过大, 不符合实际的加工需求。随着铣削力的增大, 薄壁的最大变形也增大, 且基本上呈线性增长的关系。这是因为施加的力较小, 会使薄壁产生弹性变形, 当载荷进一步增大时, 远超出薄壁弹性变形的范围, 造成不可恢复的效果, 严重影响加工后的质量和精度。因此, 在加工过程中应选择合适的切削参数, 以控制垂直于切削面的z向切削分力在一定范围内, 保证加工薄壁的精度和质量。

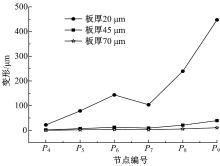
图5 切削载荷对薄壁变形的影响Fig.5 Effect of cutting force load on thin wall deformation

图6 不同板厚的位移量Fig.6 Displacement of different plate thickness

通过图6可以看出, 在节点P9上施加0.235 N的载荷时, 不同板厚的位移量相差十分大。20 μ m厚板的最大位移量约为447 μ m, 约为板厚的10倍, 45 μ m和70 μ m板的位移量均为1~40 μ m。因此, 当前的切削参数是不能够用于加工20 μ m厚的薄板的, 应当调整切削参数、降低切削用量、减小径向切削深度, 把切削力造成的位移变形减小至允许范围内。

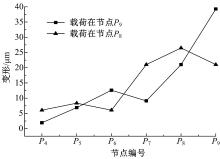
45 μ m厚板的位移量如图7所示, 当载荷施加在节点P8上时, 薄板中部(节点P5和P8)处的变形较大, 而节点P4和P6处的位移量相同, 节点P7和P9处的位移量也是相同的, 并且节点P7、P8、P9处的整体位移量要比P4、P5、P6处的大。这是由于在铣削薄壁时, 工件各部分抗弯刚度差距较大, 薄壁底部刚性大、位移量小; 顶部的刚性较弱、位移量大。当载荷施加在节点P9处时, 薄板各点位移相差较大, 节点P4处位移量接近0 μ m, 节点P9处位移量约为39.28 μ m。这是因为在铣削薄壁末端时, 结构刚性最差, 残余应力的存在会产生更大的影响, 容易引起变形波动, 导致更大的加工误差和位移量。

图7 45 μ m厚板位移量Fig.7 Deformations of 45 μ m plate

综合以上情况, 在薄壁的铣削过程中会出现切削力导致的薄壁结构位移变形, 且由于壁厚过小, 易出现弹塑性变形, 造成不可恢复的效果。因此需要对切削参数进行修正, 保证变形在弹性范围内, 提高加工精度。

4 试验验证

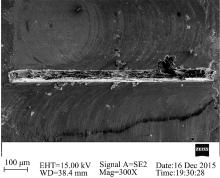
为了验证微小薄壁的加工变形, 进行了薄壁铣削试验。试验加工条件如下:主轴转速为15 000 r/min; 进给速度为0.5 mm/s; 径向切深为20 μ m; 轴向切深为600 μ m; 加工后薄壁为800 μ m× 45 μ m× 600 μ m。图8为薄壁加工后经过放大300倍的电镜扫描图。

图8 薄壁电镜扫描图(× 300)Fig.8 300 times scanning electron microscope of micro thin wall

由图7可知, 载荷施加在薄板中部节点P8处时, 最大位移变形量约为27 μ m; 载荷施加在薄板边缘节点P9处时, 最大位移变形约为39.28 μ m。由于微小薄壁在铣削后产生一定的变形恢复, 弹性恢复量约为10%。因此, 中部最大变形理论值为18.9。经过测量, 试验加工后中部的变形量约为16.7 μ m, 边缘部分的变形量约为22.3 μ m, 薄壁的边缘由于不会出现绝对的点载荷, 就不会出现巨大的变形。这样的误差可能是因为:①载荷施加时进行了一定的简化, 将较短的线力简化为点力; ②刀具的径向跳动对变形造成了一定的影响。

5 结论

(1)采用有限元方法对薄壁铣削力造成的位移变形进行了分析, 对比了载荷施加位置对位移变形造成的影响。

(2)微小紫铜薄壁切削常出现弹塑性变形, 且造成的位移变形难以恢复, 需要调整切削参数尽可能保证变形在弹性范围内, 以提高加工的精度。

(3)通过实际加工微小紫铜薄壁对铣削位移变形进行验证。试验结果表明, 有限元分析结果与试验结果有较好的一致性。

(4)加工后的紫铜薄壁会出现一些毛刺, 需采用一定的方式去除, 需要控制加工方式, 尽可能地减小薄壁铣削变形, 达到更高的精度要求。

The authors have declared that no competing interests exist.

参考文献
[1] Liu X, DeVor R E, Kapoor S G, et al. The mechanics of machining at the microscale: assessment of the current state of the science[J]. Journal of Manufacturing Science and Engineering, 2004, 126(4): 666-678. [本文引用:1]
[2] Li P, Zdebski D, Langen H H, et al. Micromilling of thin ribs with high aspect ratios[J]. Journal of Micromechanics and Microengineering, 2010, 20(11): 115013. [本文引用:1]
[3] Annoni M, Petrò S, Rebaioli L, et al. Process parameters effect on cutting forces and geometrical quality in thin wall micromilling[DB/OL]. [2016-01-09]. http://www.muprod.eu/fotos/noticias/NAMRC41-1549%20final.pdf. [本文引用:1]
[4] 戴美玲, 徐向阳, 杨福俊, 等. 薄壁球壳受刚性平面压缩的连续变形测量[J]. 光学精密工程, 2016, 24(5): 993-1000.
Dai Mei-ling, Xu Xiang-yang, Yang Fu-jun, et al. Measurement of continuous deformation of thin-walled spheres compressed by a rigid plate[J]. Optics and Precision Engineering, 2016, 24(5): 993-1000. [本文引用:1]
[5] Budak E. Analytical models for high performance milling, part I: cutting forces, structural deformations and tolerance integrity[J]. International Journal of Machine Tools and Manufacture, 2006, 46(12): 1478-1488. [本文引用:1]
[6] Tang Ai-jun, Liu Zhan-qiang. Deformations of thin-walled plate due to static end milling force[J]. Journal of Materials Processing Technology, 2008, 206(1): 345-351. [本文引用:1]
[7] Gang L. Study on deformation of titanium thin-walled part in milling process[J]. Journal of Materials Processing Technology, 2009, 209(6): 2788-2793. [本文引用:1]
[8] 郭魂, 左敦稳, 刘远伟, 等. 航空腔型薄壁件铣削变形的预测[J]. 吉林大学学报: 工学版, 2008, 38(1): 84-88.
Guo Hun, Zuo Dun-wen, Liu Yuan-wei, et al. Prediction of milling distortion for aero-thin-walled components[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(1): 84-88. [本文引用:1]
[9] Loehe J, Zaeh M F, Roesch O. In-process deformation measurement of thin-walledworkpieces[J]. Procedia CIRP, 2012, 1: 546-551. [本文引用:1]
[10] Friedrich C R, Vasile M J. Development of the micromilling process for high-aspect-ratio microstructures[J]. Journal of Microelectromechanical Systems, 1996, 5(1): 33-38. [本文引用:1]
[11] Friedrich C R. Micromechanical machining of high aspect ratio prototypes[J]. Microsystem Technologies, 2002, 8(4/5): 343-347. [本文引用:1]
[12] Bang Y, Lee K, Oh S. 5-axis micro milling machine for machining micro parts[J]. The International Journal of Advanced Manufacturing Technology, 2005, 25(9/10): 888-894. [本文引用:1]
[13] Chern G L, Wu Y J E, Cheng J C, et al. Study on burr formation in micro-machining using micro-tools fabricated by micro-EDM[J]. Precision Engineering, 2007, 31(2): 122-129. [本文引用:1]
[14] Jin X, Altintas Y. Prediction of micro-milling forces with finite element method[J]. Journal of Materials Processing Technology, 2012, 212(3): 542-552. [本文引用:1]
[15] 温学龙, 巩亚东, 程军, 等. 电镀金刚石微磨具磨损机理分析与试验研究[J]. 机械工程学报, 2015, 51(11): 177-185.
Wen Xue-long, Gong Ya-dong, Cheng Jun, et al. Mechanism analysis and experimental research on wear of electroplated diamond micro-grinding tool[J]. Journal of Mechanical Engineering, 2015, 51(11): 177-185. [本文引用:1]