高定位精度转台检测系统调整误差补偿

引用本文

鄢永耀, 刘伟, 付锦江. 高定位精度转台检测系统调整误差补偿. 吉林大学学报(工学版), 2017, 47(3): 855-860
YAN Yong-yao, LIU Wei, FU Jin-jiang. Compensation for adjustment error in high positioning accuracy turntable measuring system. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 855-860 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703023
Permissions

高定位精度转台检测系统调整误差补偿

鄢永耀^1,², 刘伟¹, 付锦江^1,²

1.中国科学院长春光学精密机械与物理研究所,长春130033

2.中国科学院大学,北京100039

作者简介:鄢永耀(1988-),男,博士研究生.研究方向:光学精密机械结构设计及优化分析.E-mail:512190699@qq.com

基金项目:“863”国家高技术研究发展计划项目(2011AA12A103); 中国地质调查局工作项目(1212011120227)

摘要

某用于实验室激光通信实验的转台要求具有±1.5″的定位精度,为了对该高定位精度转台实施检测,搭建了由24面棱体、定心装置、0.2″二维光电自准直仪和支架组成的高精度测角系统,对该测角系统进行了准直误差理论分析。结果表明:多面棱体偏心对定位精度的测量结果影响很小,一般可以忽略,但自准直仪的调整误差对高定位精度的测量影响很大。为了消除该系统误差,在理论分析的基础上,提出了一种基于角度标定的调整误差补偿的方法并进行了实验验证。通过精细调整减小调整误差方法测得转台定位精度 σ为0.936″,而采用新补偿调整误差方法测得定位精度 σ″为0 .922 ″, σ″相对 σ的相对误差为-1.496%,且满足转台定位精度要求。实验结果证明了本文方法的快速性和可靠性。

关键词: 工程测量技术; 定位精度; 误差补偿; 自准直仪; 准直误差

中图分类号:TH741 文献标志码:A 文章编号:1671-5497(2017)03-0855-06

Compensation for adjustment error in high positioning accuracy turntable measuring system

YAN Yong-yao^1,², LIU Wei¹, FU Jin-jiang^1,²

1.Changchun Institute of Optics, Fine Mechanics and Physics,Chinese Academy of Science, Changchun 130033, China

2. University of Chinese Academy of Science, Beijing 100039,China

Abstract

A turntable to be used in laser communication laboratory experiments needs positioning accuracy of ±1.5″. In order to check the technical requirements, a high accuracy angle measurement system, composed of regular polygon error, centering device, 0.2″ two-dimensional optoelectronic autocollimation and supporting, was set up. The collimation error of the system was theoretically analyzed, which shows that the off-center between the regular polygon mirror and the turntable contributes little impact on the positioning accuracy of the measurement results, which generally can be ignored. However, the adjustment error of the autocollimation has great influence on the measurement system. In order to eliminate the system error, on the basis of theoretical analysis, a new method based on data processing to compensate the adjustment error was proposed and verified by contrast experiments. Results show that a positioning accuracy σ=0.936″, was obtained by timing experiential fine adjustment, while the positioning accuracy σ″ = 0.922″ was obtained by the proposed new method. The relative error between σ″ and σ is -1.496%, which satisfies the technical requirement. Contrast experiments also demonstrate that the proposed method is convenient and reliable.

Key words: engineering survey technology; positioning accuracy; error compensation; autocollimator; collimation error

Show Figures

0 引言

捕获、瞄准及跟踪技术(Acquisition, pointing and tracking, APT)是卫星激光通信的核心技术之一^{[1, 2, 3]}, 主要用来建立卫星激光通信链路^{[4, 5]}, 并确保两通信终端能精确对准, 保障卫星通信的可靠性及稳定性^{[6, 7]}。但是在通信过程中, 卫星之间具有较大的相对运动。为了保障通信链路畅通, 要求APT系统的响应特性既快又准^[8], 所以激光通信系统对卫星平台的要求很高。本转台直径约为1.5 m, 作为实验室激光通信实验的卫星平台要求具有± 1.5″的定位精度, 对其定位精度的高精度检测是一项必不可少而又困难的工作。

为了对该高定位精度转台实施检测, 搭建了由24面棱体、定心装置、0.2″二维光电自准直仪和支架组成的高精度测角系统, 采用该检测方案时, 影响检测精度的因素很多, 主要包括安装调整误差、多面棱体的工作角偏差和光电自准直仪重复性误差等^{[9, 10]}。自准直仪重复性误差是随机误差, 可以通过多次测量减小其对测量结果的影响; 多面棱体的工作角偏差可以通过角度修正的办法来消除。而针对检测系统中调整误差对检测结果的影响, 以前的检测方案大多数是通过调整自准直仪可调底座的3个调整螺丝来仔细调整, 从而调平自准直仪^[11], 这种调整方法既费时又费力, 而且会有部分残余调整误差, 不能完全消除调整误差的影响。针对这个特点, 本文主要对检测系统中的调整误差进行理论分析, 在此基础上, 提出了一种基于角度标定的调整误差补偿新方法, 并且通过实验验证了该方法的快速性及可靠性。

1 定位精度测量原理及数据处理

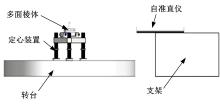
转台定位精度的测量原理如图1所示。用电子水平仪将转台调平后, 将定心装置放在转台的中心附近; 然后利用千分表对定心装置进行定心, 定心完成后, 将24面棱体固定在定心装置上, 保证转台、定心装置与多面棱体回转同步; 自准直仪安放在固定支架上^[12]。

	Figure Option View Download New Window
	图1 转台定位精度的测量原理图Fig.1 Principle diagram of turntable ’s positioning accuracy measurement

启动转台测角系统, 将转台复位到绝对零位, 利用激光笔快速将准直光管与多面棱体的零度面对准, 对准后读取准直光管的零位读数x₀。然后, 控制转台沿被测回转轴相对转动15° , 转台转动方向与多面棱体序号增大的方向一致, 记录每次转动停止稳定后二维自准直仪x方向的读数x_i(i=1, 2, …, 23)。多面棱体由于加工误差导致多面棱体各个面之间存在工作角偏差, 本检测中24面棱体的工作角偏差B_i如表1所示。

表1 多面棱体工作角偏差 Table 1 Working bias errors of polygon

不考虑准直误差时, 根据文献[13]可知, 转台各位置相对于零位的定位误差P_i、定位误差平均值 $\begin{matrix} {\bar{P}}_{i} \end{matrix}$ 和转台定位精度标准差σ 计算公式分别为:

$P_{i} = x_{i} - x_{0} - B_{i}$ （1）

${\bar{P}}_{i} = \frac{1}{24} \overset{23}{\sum_{i = 1}} (x_{i} - x_{0} - B_{i})$ （2）

$\begin{matrix} σ = \sqrt[]{\frac{1}{23} \overset{23}{\sum_{i = 1}} {(P_{i} - {\bar{P}}_{i})}^{2}} \end{matrix}$ （3）

2 调整误差分析

2.1 多面棱体安装偏心误差

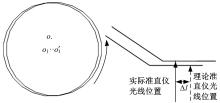
如图2所示, o为转台的回转中心; o₁为多面棱体中心; o'₁为多面棱体转动后的中心; oo₁为安装偏心e。准直光线照射在多面棱体零度角面的中心, 当多面棱体随转台逆时针转动15° 时, 由于偏心的存在, 转动后的多面棱体与转动前的多面棱体位置不重合。由几何关系可得:转动后多面棱体的各面与转动前棱体的各面互相平行, 即:安装偏心不会改变自准直仪光线和棱体照射面的倾斜角, 只会改变自准直仪光线照射在多面棱体各面上的位置。在检测时自准直仪保持不动, 光线方向不会发生改变, 由图2可知:转动后实际准直仪光线与理论准直仪光线位置不重合, 其横向距离为Δ l。

	Figure Option View Download New Window
	图2 多面棱体安装偏心Fig.2 Off-center between regular polygon mirror and turntable

由文献[2]可知:多面棱体安装偏心造成光线照射在反射面上的横向位置改变Δ l时, 由反射镜平面度引起的转台定位误差为:

$\begin{matrix} Δ_{1} = 8 h Δlρ / H^{2} \end{matrix}$ （4）

式中:H为反射面的宽度; Δ l为光线偏离理论位置的距离; h为各反射面平面度误差; ρ 为弧度与秒的转换尺度, ρ =206 265。

本实验用到的多面棱体单个反射镜的宽度H=30 mm, 平面度误差h小于60 nm。当Δ _l=0.5 mm时, 将相关参数代入式(4), 计算得到Δ ₁=0.055″, 远小于转台要求的定位精度(± 1.5″), 由此可知:本试验中多面棱体偏心对转角位置测量结果影响很小, 即在保证一定的棱体同心精度时, 安装偏心产生的误差可以忽略。

2.2 光电自准直仪调平误差

一般情况下, 在检测转台定位精度时, 自准直仪在使用前必须调平, 调平的要求为:自准直仪水平轴在± 800″范围内变化时, 竖直轴的变化量应小于10″。

利用自准直仪可调底座的3个调整螺丝及定心装置的3个可调螺母来调平, 既耗时又费力, 且无论如何都不能彻底消除调整误差, 从而导致自准直仪十字丝竖线与转台的轴线有一夹角γ ^[14]。

2.3 多面棱体相对于转台倾斜误差

转台的端面与其轴线不垂直以及多面棱体各面与转台轴线不平行导致各面与转台轴线倾斜, 用二维光电自准直仪进行转台定位精度测量时, y轴读数就是多面棱体各面与转台轴线的倾斜角β 。

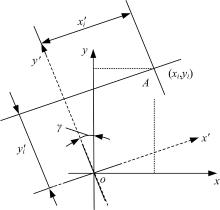
	Figure Option View Download New Window
	图3 自准直仪十字丝倾斜Fig.3 Tilt of auto-collimation crosshair

实际检测时, 光电自准直仪调平误差γ 与多面棱体各面相对于转台轴线的倾斜β 两种误差一定会共同存在, 这必然会导致检测结果产生系统误差。如图3所示, 其中y轴方向为转台轴线方向, y'轴方向为光电自准直仪十字丝竖线方向, 即:xoy为转台坐标系, x'oy'为自准直仪坐标系。

转台坐标系与自准直仪坐标系的交点为o, 是两坐标系的原点, 由于竖直方向各反射面的倾斜y_i和水平方向定位误差x_i的存在, 十字丝的交点由o点变为A点, 理论测量值为(x_i, y_i), 但由于轴线y轴与自准直仪十字丝竖线y'轴存在一夹角γ , 光电自准直仪的实际读数为(x'_i, y'_i)。

根据图3和坐标变换公式可推导出实际读数与理论测量值之间的函数关系式为:

$\begin{matrix} \{\begin{matrix} x'_{i} = (x_{i} + y'_{i} sinγ) / cosγ \\ y'_{i} = (y_{i} - x'_{i} sinγ) / cosγ \end{matrix} \end{matrix}$ （5）

实际检测时γ 值很小, 当γ < 8° 时, cosγ ≥ 0.99≈ 1, 则式(5)可简化为:

$x'_{i} = x_{i} + y'_{i} sinγ$ （6）

$\begin{matrix} y'_{i} = y_{i} - x'_{i} sinγ \end{matrix}$ （7）

式中:x_i为转台实际的零起定位误差; y_i为各面与转台轴线的倾斜值; x'_i和y'_i为自准直仪的实际读数值。

根据式(6)可求得检测系统误差Δ x_i:

$\begin{matrix} Δ x_{i} = y'_{i} sinγ \end{matrix}$ （8）

由式(8)可知:系统误差Δ x_i与y'_i和γ 值有关, 在实际检测过程中γ 值不变, sinγ 是一个常数。在检测过程中, 当y轴最大读数值为100″, γ =1° 时, Δ x_i=1.745″, 与转台要求的定位精度(± 1.5″)相当, 甚至超过要求的定位精度, 所以安装调整误差对于高精度定位精度检测的影响显著, 不能忽略。

3 准直误差补偿方法

由式(8)可知:系统误差Δ x_i主要取决于自准直仪y'轴读数和转台坐标系与自准直仪坐标系之间的旋转角γ 。在同一组测量时, 自准直仪一般保持不动, 即γ 不变, 而y'_i可以通过自准直仪的y'轴读取, 所以为了消除系统误差, 关键在于标定出γ 。基于此原理, 本文提出了一种新的系统误差补偿方法:转台复位, 将自准直仪与多面棱体零位对准, 记录二维光电自准直仪的两维初始读数, 启动测角系统, 转台转动一微小角度, 记录读数, 依次进行, 直至转角超出了自准直仪的量程, 将得到的二维值进行线性拟合得到一条直线。根据式(7)可知:拟合直线的斜率k即为-sinγ , x'_i、y'_i通过自准直仪读取, 将实验值代入式(6), 即可得到转台实际的零起定位误差式(9), 从而消除调整误差。

$\begin{matrix} x_{i} = x'_{i} + ky'_{i} \end{matrix}$ （9）

将式(9)代入式(1)即可得到采用补偿方法得到的转台各位置相对于零位的定位误差计算公式:

$\begin{matrix} P_{i} = x_{i} - x_{0} - B_{i} = x'_{i} + ky'_{i} - x_{0} - B_{i} \end{matrix}$ （10）

这种方法对检测前的调整要求不高, 只要保证在整个检测过程中竖直方向的偏角在准直仪量程内即可, 不需要精调, 调整难度大大减小, 而且消除了系统误差。

4 实验验证及数据处理

图4为实验台装置图。图5为利用千分表进行定心的实验装置。为了验证补偿方法的准确性, 本文做了一个对比实验:第1组实验利用传统方法, 即通过数小时精心调整检测系统, 使转台转动时准直光管y'轴读数的变化不超过10″, 将其理论计算结果作为转台的实际定位精度, 实验数据及其数据处理结果如表2所示; 第2组实验是在第1组实验装置的基础上, 旋转定心装置3个螺杆中的1个螺杆, 增大调整误差, 然后按第3节描述的方法进行偏角γ 的标定, 实验数据如表3所示, 大调整误差下定位精度检测的实验数据如表4所示。

	Figure Option View Download New Window
	图4 实验台装置图Fig.4 Diagram of experimental devices

	Figure Option View Download New Window
	图5 利用千分表进行定心实验装置图Fig.5 Diagram of experiment devices used to center with indicator

将表2中的角位移误差代入式(3), 可得σ =0.936″, 此为传统方法得到的结果, 包含一定的系统误差, 但该误差比较小, 因为当转台转动时, 自准直仪y'轴读数变化最大为11.8-(-0.7)=12.5"。针对表4中的数据, 如果不考虑调整误差的影响, 按照式(1)~(3)可以求得σ '=3.693″, 此为未进行补偿时粗略调整后的结果, 与表2计算结果得到的实际转台定位精度对比相差很大, 说明检测结果有误, 即调整误差不能忽略, 需要对误差进行补偿。

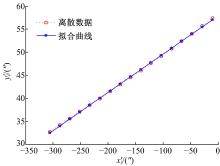
利用Matlab对表2中的数据进行拟合, 拟合结果如图6所示, 可知直线斜率k=-sinγ =0.083 20。利用式(9)可得转台实际的零起定位误差x_i, 计算结果列于表4中, 将计算结果代入式(3)即可得转台定位精度σ ″=0.922″。首先, 该值与σ '相比减小了69.92%, 即通过误差补偿大大提高了测量所得的定位精度; 其次, 该值与σ 的相对误差仅为-1.496%, 并且更小于此精确调整的结果, 即精度更高; 最后, 补偿结果σ ″与技术要求的± 1.5″相比精度提高了38.53%, 足够满足此高精度转台的理论定位精度要求。综上, 实验结果很好地验证了本文误差补偿方法快速、有效。

表2 第1组定位精度检测实验数据 Table 2 Positioning accuracy experimental data of first group

表3 偏角γ 标定的实验数据 Table 3 Experiment data of calibration about angle γ

表4 大调整误差下定位精度检测的实验数据 Table 4 Experimental positioning accuracy with large adjustment error

	Figure Option View Download New Window
	图6 标定数据拟合直线Fig.6 Curve fitting of calibration data

5 结束语

分析了调整误差对某用于激光通信实验的高精度转台定位精度检测结果的影响。结果表明:在满足测量条件下, 多面棱体的偏心对检测结果的影响比较小, 一般情况下可以忽略不计。光电自准直仪调平误差对高精度转台定位精度的检测结果影响很大, 一般都是通过反复长时间调节测角系统减小调整误差, 但这种方法费时费力, 又不能完全消除系统误差, 而利用本文方法, 借助Matlab软件进行角度标定, 可以准确、快速地完成高精度转台定位精度的检测, 在满足转台要求的基础上, 既缩短了检测前的准备时间又可以快速消除系统误差, 利于后续激光通信相关实验的开展。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	赵馨, 宋延嵩, 佟首峰, 等. 空间激光通信捕获、对准、跟踪系统动态演示实验[J]. 中国激光, 2014, 41(3): 0305005. Zhao Xin, Song Yan-song, Tong Shou-feng, et al. Dynamic demonstration experiment of acquisition, pointing and tracking system in space laser communications[J]. Chinese Journal of Lasers, 2014, 41(3): 0305005. [本文引用:1]
[2]	郑燕红. 卫星激光通信终端系统捕获瞄准跟踪技术研究[D]. 哈尔滨: 哈尔滨工业大学航天学院, 2012. Zheng Yan-hong. Research on acquisition pointing and tracking of satellite laser communication terminal[D]. Harbin: School of Astronautics, Harbin Institute of Technology, 2012. [本文引用:1]
[3]	Mohan S, Alvarez-Salazar O, Birnbaum K, et al. Pointing, acquisition, and tracking architecture tools for deep-space optical communications[C]//SPIE, San Francisco, California, USA, 2014: 89710H. [本文引用:1]
[4]	姜会林, 佟首峰. 空间激光通信技术与系统[M]. 北京: 国防工业出版社, 2010. [本文引用:1]
[5]	Toyoshima M. Optical space communication in Japan[J]. Function Materials, 2003, 10(3): 428-437. [本文引用:1]
[6]	Tolker-Nielsen T, Oppenhaeuser G. In-orbit test result of an operational optical intersatellite link between ARTEMIS and SPOT4, SILEX[C]//SPIE, San Francisco, California, USA, 2002: 1-15. [本文引用:1]
[7]	Lesh J R. Deep space optical communications development program[C]//Optical Technologies for Space Communication Systems, Los Angeles, CA, USA, 1987: 8-11. [本文引用:1]
[8]	王绍举, 金光, 徐开. 高精度激光通信小卫星星座仿真平台设计[J]. 光学精密工程, 2008, 16(8): 1554-1559. Wang Shao-ju, Jin Guang, Xu Kai. Design of simulation platform for high precision laser communication small satellite constellation[J]. Optics and Precision Engineer, 2008, 16(8): 1554-1559. [本文引用:1]
[9]	郭敬滨, 曹红艳, 王克新, 等. 转台分度误差检测及补偿技术的研究[J]. 中国机械工程, 2014, 25(7): 895-899. Guo Jing-bin, Cao Hong-yan, Wang Ke-xin, et al. Study on verification and compensation of indexing errors for turntable[J]. China Mechanical Engineering, 2014, 25(7): 895-899. [本文引用:1]
[10]	吴世臣. 卫星光通信终端二维转台轴系误差分析及补偿方法研究[D]. 哈尔滨: 哈尔滨工业大学航天学院, 2007. Wu Shi-chen. Analyse of axis-errors and compensating in terminal of intersatellite optical communication[D]. Harbin: School of Astronautics, Harbin Institute of Technology, 2007. [本文引用:1]
[11]	曹学东, 范天泉, 吴时彬, 等. 几何量测量技术进展[J]. 红外与激光工程, 2008, 37(5): 884-889. Cao Xue-dong, Fan Tian-quan, Wu Shi-bin, et al. Current developments of measurement techniques for geometry parameters[J]. Infrared and Laser Engineering, 2008, 37(5): 884-889. [本文引用:1]
[12]	苏燕芹, 张景旭, 陈宝刚, 等. 谐波分析方法在提高精密转台回转精度中的应用[J]. 红外与激光工程, 2014, 43(1): 274-278. Su Yan-qin, Zhang Jing-xu, Chen Bao-gang, et al. Harmonic analysis application in accuracy improvement of precise turntable[J]. Infrared and Laser Engineering, 2014, 43(1): 274-278. [本文引用:1]
[13]	张东纯, 蒋亚红. 多面棱体工作面偏差补偿的符号问题[J]. 测控技术, 2008, 27(3): 94-95. Zhang Dong-chun, Jiang Ya-hong. Error compensation of reflecting plane of polygons[J]. Measurement & Control Technology, 2008, 27(3): 94-95. [本文引用:1]
[14]	孙方金. 自准直仪与反光面准直时的注意事项[J]. 计量技术, 1999(10): 33-36. Sun Fang-jin. The collimation announcements between the reflective surface and the autocollimator[J]. Measurement Technique, 1999(10): 33-36. [本文引用:1]

2014

0.0

. 2014, 41(3):0305005-

Dynamic demonstration experiment of acquisition, pointing and tracking system in space laser communications

空间激光通信捕获、对准、跟踪系统动态演示实验

Zhao Xin , Song Yan-song , Tong Shou-feng

赵馨, 宋延嵩, 佟首峰

摘　要：捕获、对准、跟踪（APT）系统是空间激光通信重要组成部分，是通信正常进行的前提与保障。对APT系统组成原理、工作原理、关键技术、系统设计、工程实现等内容进行了详细的研究，在此基础上开展室内模拟实验及野外演示验证实验。室内模拟实验跟踪精度达到2～3μrad，表明本系统可应用在星间激光通信中。野外双端动态演示实验在飞艇一船舶间进行，结果表明系统捕获概率优于95％，捕获时间小于60s，系统跟踪精度由于受到大气湍流影响而降低，多次实验测试表明在湍流中跟踪精度达到5～25μrad。APT系统的成功研制为空间激光通信顺利进行奠定了基础。

... 0 引言捕获、瞄准及跟踪技术(Acquisition,pointing and tracking,APT)是卫星激光通信的核心技术之一^[1,2,3],主要用来建立卫星激光通信链路^[4,5],并确保两通信终端能精确对准,保障卫星通信的可靠性及稳定性^[6,7] ...

2012

0.0

. 2012, :-

Research on acquisition pointing and tracking of satellite laser communication terminal[D]. Harbin:School of Astronautics,

卫星激光通信终端系统捕获瞄准跟踪技术研究[D]

Zheng Yan-hong.

郑燕红

卫星激光通信是利用激光作为载波信号的一种重要的卫星通信方式,它是构成未来外层空间通信网络,星地通信网络的基础。本文结合卫星激光通信捕获、瞄准、跟踪过程,侧重研究了终端对对方终端位置的预测及搜索方案,针对对方光束位置提取过程中的图像处理问题,以及实现捕获瞄准跟踪过程的控制系统鲁棒稳定性、干扰抑制等问题进行了系统、深入地分析与设计: 首先,针对激光通信链路的建立和保持过程,介绍了终端系统的各个组成单元,通过对典型终端机械结构及组成的分析,讨论了卫星激光通信终端系统的捕获、瞄准、跟踪过程以及相应的任务,并对扫瞄捕获过程中的捕获概率的约束因素进行了分析,通过对开关键控编码、曼彻斯特编码以及脉冲位置调制编码下的误码率大小进行了分析。其次,考虑到卫星平台轨道、姿态的运动对激光通信光束指向的影响和远距离通信过程中激光传输时间问题,采用坐标变换和直接建立相对运动微分方程组两种方案推导了摄动影响下的光通信终端天线的预测指向角,并对在轨卫星采用两种方案得到的预测指向角进行了仿真分析。由于在链路建立阶段需要通过扫瞄过程实现对目标的捕获,分析比较了三种扫瞄方案,提出了有效覆盖因子来表征单个光束投影的覆盖率,并结合预设重叠因子设计了常见扫瞄方式下的快速扫瞄与完全覆盖的扫瞄点放置方案,并获得了终端在扫瞄过程中应附加输入的扫瞄角变化规律,仿真显示确实能综合解决完全覆盖和快速完成扫瞄两个问题。再次,分析了探测器靶面上形成的光斑坐标与光束入射角的关系,并推导了终端天线和快速倾斜镜分别作为执行机构时相应的反馈角度提取方法。由于图像中混杂的噪声信号对光斑中心坐标计算有较大影响,提出了根据能量、面积的大小将灰度图象噪声分为孤立噪声点和恒星背景噪声两类进行滤波处理。在孤立噪声处理过程中提出了两种方案:一是利用Sobel算子结合梯度倒数形成动态模板加权平滑,然后通过最大类间方差法阈值分割实现噪声滤除;二是结合小波变换的时频局部性和神经网络的自学习能力,利用小波神经网络作为图像滤波器对噪声进行消除。而针对恒星背景噪声,提出了连通区域选择扩张方案和基于Canny算子边缘提取与K-均值聚类方案,对恒星背景噪声进行分离,结合孤立噪声与背景噪声滤波方法对灰度图像进行仿真处理,取得了良好的滤除效果。然后,针对光通信控制系统中终端天线与快速倾斜镜两个内回路的物理部件特性进行了分析,指出控制对象模型的不确定性;并分析了控制器由于量化误差、器件老化等因素可能引起的参数摄动;结合光通信系统的特点,总结了系统的内外部扰动信号,通过具体的仿真过程论证了扰动对系统的影响。针对终端天线回路的模型不确定性、控制器摄动和扰动信号的影响提出了鲁棒H∞控制器设计方法,对于快速倾斜镜回路由于时滞环节的影响,基于Lyapunov函数设计了时滞鲁棒H∞控制器,通过仿真分析验证了内回路对干扰和模型摄动的鲁棒性。最后,以终端天线与快速倾斜镜回路为基础构成了光通信捕获、瞄准、跟踪过程的捕获、瞄准阶段光通信终端控制系统,稳定性问题值得关注,基于终端天线与快速倾斜镜回路建立了光通信控制系统模型,通过时滞系统稳定性条件和矩阵测度稳定性条件分析了整个光通信控制系统的稳定性,并对终端天线与快速倾斜镜回路的设计进行了校验。为了完善整个设计过程,从时滞稳定性条件出发,采用公共的变换阵与锥补法推导了终端天线与快速倾斜镜回路鲁棒H∞状态反馈设计下确保整个系统稳定的约束设计方法。

2014

0.0

2010

0.0

2003

0.0

2002

0.0

1987

0.0

2008

0.0

. 2008, 16(8):1554-1559 DOI:doi:10.3321/j.issn:1004-924X.2008.08.034

Design of simulation platform for high precision laser communication small satellite constellation

高精度激光通信小卫星星座仿真平台设计

Wang Shao-ju , Jin Guang , Xu Kai.

王绍举, 金光, 徐开

针对小卫星星座中卫星间激光通信的要求,提出了一种高精度激光通信小卫星星座仿真平台,该平台由两个模拟卫星和一个控制中心组成。模拟卫星以高精度三轴气浮转台为卫星平台,由星务计算机和各种星上姿态敏感器及姿态执行器构成,高精密气浮转台为卫星提供仿真工作环境,星务计算机、姿态敏感器及执行器为卫星平台实现高精度的指向提供了保障。该仿真平台可根据任务需要进行双星主从控制、双星协同控制、三星主从控制、三星协同控制和单星故障控制仿真,仿真结果表明,提出的仿真平台可以满足小卫星星座激光通信的要求,为下一步深入研究小卫星星座激光通信及小卫星星座智能控制技术提供了参考依据。

... 为了保障通信链路畅通,要求APT系统的响应特性既快又准^[8],所以激光通信系统对卫星平台的要求很高 ...

2014

0.0

. 2014, 25(7):895-899 DOI:doi:10.3969/j.issn.1004-132X.2014.07.009

Study on verification and compensation of indexing errors for turntable

转台分度误差检测及补偿技术的研究

Guo Jing-bin , Cao Hong-yan , Wang Ke-xin

郭敬滨, 曹红艳, 王克新

采用0.3"的精密多齿分度台与平面反射镜组合,对转台分度误差进行检测.针对多齿分度台安装倾斜对检测结果产生影响的问题,提出了利用双轴光电自准直仪Y轴读数补偿调整误差的方法.根据转台分度误差是由多次谐波叠加的特点,采用谐波分析的方法对测量得到的离散数据进行拟合处理,得到用于转台分度误差补偿的连续曲线模型.对分度误差为17.82"的转台进行实测和误差补偿,补偿后转台的最大分度误差为2".

... 2″二维光电自准直仪和支架组成的高精度测角系统,采用该检测方案时,影响检测精度的因素很多,主要包括安装调整误差、多面棱体的工作角偏差和光电自准直仪重复性误差等^[9,10] ...

2007

0.0

. 2007, :-

Analyse of axis-errors and compensating in terminal of intersatellite optical communication[D]. Harbin:School of Astronautics,

卫星光通信终端二维转台轴系误差分析及补偿方法研究[D]

Wu Shi-chen.

吴世臣

卫星光通信与微波通信相比具有通信容量大、终端体积小和保密性好等特点，将是未来卫星通信技术的重要发展方向。近年来，卫星光通信技术的研究受到了许多国家的重视，在美国、欧洲、日本和俄罗斯等国家和地区获得了发展。我国也已开始重视卫星光通信技术的研究，并取得了一定成果。在卫星间激光链路的建立和保持中，角度偏差检测被用来校正捕获和跟踪的误差。角度偏差检测系统的精度极大程度地影响着瞄准、捕获和跟踪的性能，对星间链路的建立起着至关重要的作用。由于激光光场光束窄，星间距离大，使得卫星光通信终端安装精度对PAT性能的影响增大。因此分析终...

2008

0.0

. 2008, 37(5):884-889 DOI:doi:10.3969/j.issn.1007-2276.2008.05.032

Current developments of measurement techniques for geometry parameters

几何量测量技术进展

Cao Xue-dong , Fan Tian-quan , Wu Shi-bin

曹学东, 范天泉, 吴时彬

为将排列互比法用于超精测角研究、大型机械零部件形位误差在位测量技术研究及非球面主镜面形误差测量技术研究等几何量测量课题,在理论分析及实验验证的基础上推导出了排列互比法理论公式及系统误差产生的原因,在优化组合传统检验方法的基础上提出了大型机械零部件形位误差测量方案,并解决了Φ4.5 mx5 m高精度机架测量难题,采用拼接技术、哈特曼技术及补偿技术等解决了Φ1.8 m大口径非球面主镜面形误差测量难题.

... 而针对检测系统中调整误差对检测结果的影响,以前的检测方案大多数是通过调整自准直仪可调底座的3个调整螺丝来仔细调整,从而调平自准直仪^[11],这种调整方法既费时又费力,而且会有部分残余调整误差,不能完全消除调整误差的影响 ...

2014

0.0

. 2014, 43(1):274-278 DOI:doi:10.3969/j.issn.1007-2276.2014.01.048

Harmonic analysis application in accuracy improvement of precise turntable

谐波分析方法在提高精密转台回转精度中的应用

Su Yan-qin , Zhang Jing-xu , Chen Bao-gang

苏燕芹, 张景旭, 陈宝刚

In order to increase the angular position measurement accuracy and improve structure design of a precise turntable, the angular position measurement precision of its azimuth shafting was detected. The error included axial error, encode error and other errors. Fourier harmonic analysis was adopted in data processing. Harmonic waves with different orders were used to fit the data, low order harmonic waves were removed, which could increase the position measure accuracy. Meanwhile, the error sources had been found. The error look up table could be used to correct the measure data afterward. As the result shows, the value of angular position measurement error after corrected is 1/4 of the value before corrected, the amplitude is about 0.8", the angular position measurement accuracy has been increased a lot. A look up table was built to correct post -measurement data; the error sources were found, which will help to improve the shafting structure.

为了提高某精密转台的测角精度和改进结构设计，对其方位轴系角位置测量精度进行了检测，该误差包括轴系误差、编码器误差及其他误差项。在数据处理中，采用傅里叶谐波分析方法，用不同阶次的简谐波进行拟合，去掉低阶误差，可提高位置测量精度，同时分析了各误差的来源。建立的误差查询表格可用于对后期测量结果的修正。结果证明，角位置测量误差修正后的值是修正前的1/4左右，幅值不超过0.8"，极大地提高了角位置测量精度。此实验研究了使用谐波分析来提高转台位置测量精度的方法；同时分析了各误差来源，便于采取相应措施对轴系进行改进。

... 自准直仪安放在固定支架上^[12] ...

2008

0.0

. 2008, 27(3):94-95 DOI:doi:10.3969/j.issn.1000-8829.2008.03.032

Error compensation of reflecting plane of polygons

多面棱体工作面偏差补偿的符号问题

Zhang Dong-chun , Jiang Ya-hong.

张东纯, 蒋亚红

讨论了利用多面棱体和自准直仪进行精密角度检定时多面棱体工作面偏差的补偿问题,给出了工作面偏差补偿符号的判定方法.

0.0

. , 1999(10):33-36

The collimation announcements between the reflective surface and the autocollimator