金属板材三维曲面零件广泛应用于车辆、船舶、航天航空以及建筑等军用和民用领域。三维曲面的成形方法有很多, 除传统的刚性模具成形外, 多点成形技术作为三维曲面柔性加工方法也已经成功应用到多个领域^[1], 然而多点成形设备高昂的研制费用限制了其应用的广泛性。可挠辊卷板成形是Yamashita等^[2]最早提出的三维曲面连续成形方法, 工作零件2根可挠辊和2根辅助辊组成, 可挠辊由多个分段直辊按照弯曲轮廓排列而成, 辊间以联轴器联接, 由于分段直辊在联接处不连续, 成形的曲面会产生纵向压痕, 光顺性较差。线性增量滚弯成形是Shim等^{[3, 4]}提出的三维曲面连续成形方法, 成形零件由3对共6根工作辊组成, 每根工作辊由多个独立短辊按照弯曲轮廓排列而成, 由于短辊的独立性, 其与板料的接触为离散式接触, 成形轮廓非连续, 难以保证成形曲面的质量。连续柔性成形是李明哲等^{[5, 6]}提出的三维曲面连续成形方法, 工作零件由1根上柔性辊、2根下柔性辊组成, 柔性辊为多层缠绕的钢丝构成的软轴, 软轴弯曲轮廓可控, 可绕自身的弯曲轴线转动。由于柔性辊是钢丝缠绕而成, 成形曲面易出现钢丝划痕, 不便于后续处理。

柔性轧制成形是一种全新的三维曲面连续成形方法^{[7, 8, 9, 10]}, 该方法融合了传统的轧制技术和柔性多点控制技术于一体, 工作零件由2根柔性可弯辊组成, 通过控制2根工作辊的弯曲程度和辊缝分布就可以简单、快速地轧制成形三维曲面, 成形曲面光滑连续、无划痕。曲面轧制成形过程中板料的塑性变形较大, 与基于弯曲变形理论的曲面成形方法相比, 成形件回弹小。柔性轧制成形是一种横向变形基于弯曲理论、纵向变形基于不均匀减薄轧制理论的新的成形方式, 这种成形方式对成形曲面质量有重要影响, 因此对曲面变形过程进行分析, 掌握其成形规律、分析其成形效果十分必要。

本文从应力、应变角度出发对柔性轧制曲面的变形过程进行分析, 采用有限元模拟的方法对曲面成形规律进行研究, 并通过试验对该方法进行成形效果验证。

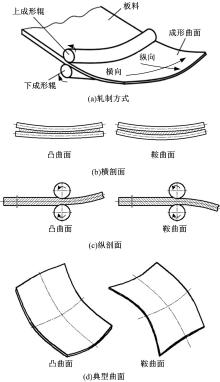
板料金属三维曲面柔性轧制成形是一种特殊的轧制方式。图1为柔性轧制成形原理图, 设备采用2根轴线可弯曲的轧辊作为成形工具, 轧辊截面为圆形, 直径较小, 采用特殊材料制成, 工作时能够在控制系统的控制下实现小挠度弯曲并且可以绕自身的弯曲轴线转动, 如图1(a)所示。在支撑机构的支撑作用下, 多点控制机构对轧辊进行调形, 使上、下轧辊产生不同程度的挠曲变形, 调形后的两轧辊曲率半径不同, 且非同心, 辊缝呈非均匀分布, 通过控制上成形辊的下移量来控制两辊间的最小缝隙宽度, 并使板料产生横向弯曲变形, 如图1(b)所示。工作时驱动机构对上、下成形辊施加转矩, 依靠辊与板料之间的摩擦力带动板料连续进给, 使板料从辊缝间连续经过被轧制减薄, 产生纵向弯曲变形, 如图1(c)所示。根据成形曲面的需要, 可通过控制机构改变轧辊的弯曲轮廓、辊缝分布形式和最小辊缝间隙, 用以成形不同形状和尺寸的三维曲面。若辊缝按照中间辊缝小边缘辊缝大排列时, 横向弯曲与纵向弯曲变形方向相同, 形成凸曲面; 反之, 若辊缝按照中间辊缝大边缘辊缝小排列时, 横向弯曲与纵向弯曲变形方向相反, 形成鞍曲面, 如图1(d)所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 柔性轧制成形原理Fig.1 Principle of flexible rolling forming

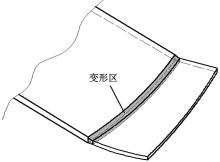
由柔性轧制成形原理知道柔性轧制成形是局部连续成形, 板料与柔性辊的接触变形区域是窄而长的条形区域, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 变形区示意图Fig.2 Schematic diagram of deformation zone

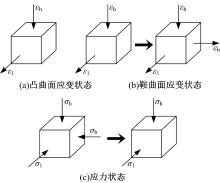
为了分析板料在柔性轧制成形过程中的变形情况, 任取变形区中的微元体进行分析。图3为变形前、后板料中心和边缘单元的变形情况, 成形凸曲面时两侧单元厚度没有变化, 越到中间单元厚度减薄越大。成形鞍曲面时中间单元厚度没有变化, 越往两侧单元厚度减薄越大。

图3

Fig.3

	Figure Option ViewDownloadNew Window
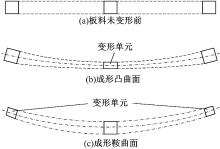	图3 板料变形前、后中心和边缘单元变形情况对比Fig.3 Shape comparison of center and edge elements before and after sheet forming

设变形区内任意变形单元的主应力和主应变方向分别为横向(σ _b、ε _b)、纵向(σ _l、ε _l)、厚向(σ _h、ε _h)。由于柔性轧制成形是以板料厚度减薄为主的变形过程, 塑性变形程度大, 弹性变形可以忽略, 即认为满足体积不变条件, 变形区内任一点满足ε _b+ε _l+ε _h=0。成形过程中板料厚向承受轧辊的压缩作用, 从而产生纵向和横向流动。如图2所示, 变形区内沿板料宽度方向的尺寸远远大于沿纵向和厚度方向的尺寸, 根据最小阻力定律, 变形区中部单元只有纵向伸长没有横向宽展, 即变形区中部为平面应变状态, ε _h< 0, ε _b=0, ε _l> 0。成形凸曲面时变形区自由端附近单元没有受压减薄, 宽展可以忽略(见图4(a)); 成形鞍曲面时变形区自由端附近单元受压减薄, 既有纵向伸长也有横向宽展, ε _h< 0, ε _b> 0, ε _l> 0。所以, 变形区的应变状态为:从中间部位的平面应变状态逐渐变为两侧的三向应变状态, 如图4(b)所示。但是, 就整体情况来说, 板料的厚度远小于板料的宽度, 变形区沿宽度方向尺寸远远大于另外两个方向尺寸, 成形时宽展量极小, 可以忽略, 即认为板料在宽度方向上的应变近似为零(ε _b≈ 0)。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 变形单元的应变和应力状态Fig.4 Stress and strain state of deformation element

轧制成形时板料的变形区中间部位受到轧制力使厚度减薄, 纵向伸长, 由于材料之间的相互牵制, 板料不能自由变形, 板料在纵向上的伸长受到阻碍, 纵向应力为压应力σ _l< 0, 同样横向也受到压应力σ _b< 0, 厚向上受到轧制压应力σ _h< 0, 因此, 中间部位呈三向压应力状态。板料两侧自由端横向上不受力, 呈平面应力状态。所以, 变形区的应力状态为:从中间部位的三向压应力状态逐渐变化为两侧的平面应力状态, 如图4(c)所示。变形单元的变形情况为厚度减薄, 宽度近似不变, 纵向延展伸长。

设板料在3个方向上的变形系数分别为:

η=H/hβ=b/Bδ=l/L(1)

式中:η 为压下系数; β 为宽展系数; δ 为纵向延伸系数; H、h分别为板料入口和出口厚度; B、b分别为板料入口和出口宽度; L、l分别为板料变形前和变形后纵向长度。

根据塑性变形体积不变原理, 3个系数之间的关系为:

η=βδ2

由于横向宽展可忽略不计, 即β =1, 式(2)可简化为:

η=δ3

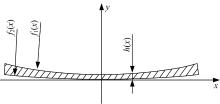
截取板料变形区横截面, 并建立以中心单元厚向为y轴, 水平方向为x轴的坐标系, 如图5所示, 上、下成形辊的调形形状不一致, 设上辊的调形函数为f₁(x), 下辊的调形函数为f₂(x), 则成形曲面的厚度分布函数为h(x)=f₁(x)-f₂(x)。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 变形区横截面示意图Fig.5 Schematic diagram of cross-section of deformation zone

由于不计宽展, 沿x向的纵向轧制应变为:

εl(x)=-εh(x)=-lnh(x)H(4)

轧制成形后沿x向的纵向纤维长度为:

l(x)=LHh(x)=Lexp[-εh(x)]=Lexp[εl(x)]（5）

根据Mises屈服准则, 可以得出变形区横截面上任一点的等效应变为:

ε-=29(εl-εb)2+(εb-εh)2+ (εh-εl)2]12=23εl(6)

不均匀的辊缝分布导致金属纵向上的不均匀伸长, 进而导致横向上材料以不同的速度出辊, 由于成形件是一个整体, 必然造成金属之间的相互牵制, 这种相互作用力使板料出辊后沿横向转动, 形成纵向弯曲变形, 板料的这种不均匀变形是其形成三维曲面的根本原因。

为进一步研究成形后板料的变形情况, 采用ABAQUS有限元软件对两种曲面件的成形过程进行模拟。有限元模型如图6所示, 模拟时采用离散辊建模方式, 显式动力学算法。接触分析时离散辊外表面为主面, 板料表面为从面。接触属性包括法向和切向, 法向接触选用硬接触, 接触面之间能够传递的接触压力大小不受限制, 当接触压力变为零或负值时, 两个接触面分离, 并去掉相应节点上的接触约束; 切向接触选用库伦摩擦模型, 罚函数算法, 成形过程无润滑, 摩擦因数按工程经验设为0.2。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 柔性轧制成形有限元模型Fig.6 Finite element model of flexible rolling forming

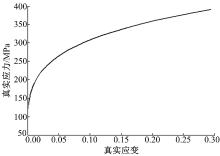
板料毛坯选用200 mm× 120 mm× 1 mm的08AL钢板, 横向目标曲率半径为500 mm, 采用圆弧形阵列排辊方式。08AL的弹性模量E=207 GPa; 泊松比μ =0.29; 密度ρ =7800 kg/m³; 屈服强度σ _s=180 MPa, 应力应变曲线如图7所示。为节省计算资源, 采用1/2有限元模型进行计算。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 08AL应力-应变曲线Fig.7 Stress-strain curve of 08AL

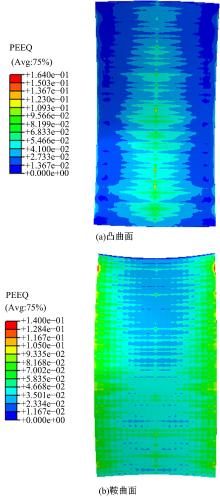
图8为成形件的等效应变云图, 从图中可以看出:凸曲面件横向对称中心处等效应变最大, 从对称中心到两侧边缘应变越来越小。鞍曲面的等效应变规律与凸曲面相反。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 等效应变云图Fig.8 Contour of PEEQ

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 横纵向截面线选取Fig.9 Selection of section lines in transverse and longitudinal direction

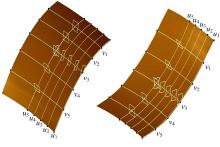
为了分析成形后板料的变形情况, 提取成形曲面件模拟结果的中间层, 并从横、纵两个方向的不同位置分别选取截面曲线(见图9)进行对比分析, u₁~u₅为成形件横向主曲率曲线的法平面与成形件相交所得的截线; v₁~v₅为成形件纵向主曲率曲线所对应弦线上的法平面与成形件相交所得的截线。

横向截面线可以随机选择, 这里选取图中v₁, v₃, v₅进行测量, 测量单位为1个单元。由于成形零件形状在横向上沿中心对称, 故选取对称中心一侧的纵向截面线进行测量, 这里选取离图中左侧边缘距离为60、90、120 mm处的截面线, 即图中的u₅, u₃, u₁进行测量。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 成形件横向单元宽度对比Fig.10 Width comparison of transverse element of part

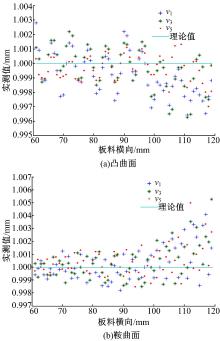
图10为成形件不同截面线上的单元宽度沿横向上的分布, 根据成形件对称性, 这里只测量了对称中心一侧的截面线。从图10(a)中可以看出, 成形凸曲面时曲面中间部分的金属单元宽度沿理论值上下波动, 其宽展均值几乎为零, 该区域为平面应变, 而边缘部位单元宽度不但没有宽展, 而且多数单元宽度还略有缩减, 经分析边缘部位单元产生负宽展是由于成形凸曲面时中间部位辊缝小, 板料厚度减薄量大, 金属沿纵向延展大于两侧, 结果在两侧引起张应力, 引起边缘成形区宽度的收缩, 进而靠近边缘部位的单元产生了负宽展。但是综合来看, 单元宽度的实测值围绕理论值震荡, 变化范围为-0.004~0.003 mm, 横向变化并不明显。图10(b)显示成形鞍曲面时曲面中间部位宽展均值近视为零, 而边缘位置附近多数单元为正宽展, 综合来看单元宽度的实测值围绕理论值震荡, 变化范围为-0.002~0.006 mm, 横向上宽展总量很小。

图11为理想排辊方式成形曲面时不同压下率下各纵向截面线的纵向延伸量对比图。从图11可以看出:无论是成形凸曲面还是鞍曲面, 同一截面位置压下率越大, 纵向截面线的延伸量越大。成形凸曲面时, 纵向中心线延伸量最大, 从中心到两侧呈递减趋势, 边缘的延伸量随压下率的变化很小; 成形鞍曲面时, 变化规律与凸曲面相反。

图11

Fig.11

	Figure Option ViewDownloadNew Window
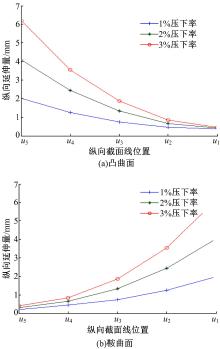	图11 不同压下率下纵向截面线延伸量对比Fig.11 Elongation comparison of longitudinal section line under different reduction rates

图12为横向弯曲半径不变时, 不同压下率情况下纵向主曲率曲线的弯曲状态对比, 从图中可以看出不论是凸曲面还是鞍曲面, 纵向曲率半径都随着压下率的增加而减小, 其原因是压下率越大, 辊缝相对高度越大, 板料的相对减薄量越大, 纵向纤维的相对伸长量越大, 纵向变形程度越大, 纵向曲率半径越小。

图12

Fig.12

	Figure Option ViewDownloadNew Window
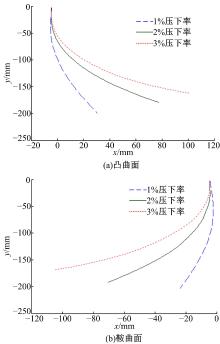	图12 不同压下率下纵向中心线弯曲状态对比Fig.12 Bending state comparison of longitudinal center line under different reduction rates

图13

Fig.13

	Figure Option ViewDownloadNew Window
	图13 横纵曲率半径关系Fig.13 Relationship between transverse and longitudinal curvature radius

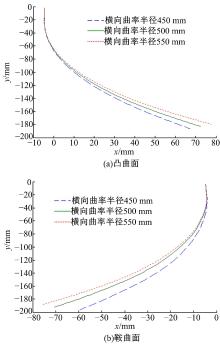
图13为压下率不变情况下, 横纵曲率半径的关系曲线, 图中显示, 不论是凸曲面还是鞍曲面, 纵向曲率半径随着横向曲率半径的增大而减小, 原因是横向弯曲半径越大, 调整辊形后的辊缝相对高度越大, 纵向纤维的相对伸长量越大, 纵向曲率半径越小。

图14为基于柔性轧制成形原理研发的试验装置, 上、下柔性辊直径均为5 mm, 每个辊分别设有10个调形控制点。

图15为使用该装置成形出的曲面件, 材料及毛坯尺寸与前述模拟选择一致。凸曲面件的横向目标曲率半径为500 mm, 纵向目标曲率半径为350 mm; 鞍曲面件的横向目标曲率半径为500 mm, 纵向目标曲率半径为300 mm。利用PRO CMM激光扫描仪对试验件进行扫描分析, 逆向出扫描点云曲面, 并按图9所示截面位置提取截面线进行测量, 测量数值如表1所示, 与目标曲率半径相比成形凸曲面的最大成形误差为2.7 mm, 成形鞍曲面的最大成形件误差为3.2 mm,

图14

Fig.14

	Figure Option ViewDownloadNew Window
	图14 柔性轧制成形装置Fig.14 Device of flexible rolling forming

图15

Fig.15

	Figure Option ViewDownloadNew Window
	图15 成形的曲面件Fig.15 Curved surface parts formed

表1

Table 1

表1(Table 1)

表1 横、纵截面线曲率半径对比 Table 1 Curvature radius comparison of transverse and longitudinal section line 截面线 序号 横向曲率半径/mm 纵向曲率半径/mm v1 v3 v5 u1 u3 u5 凸曲面 502.2 501.8 502.7 352.1 351.4 351.0 鞍曲面 502.6 502.1 503.2 302.6 302.3 301.7

表1 横、纵截面线曲率半径对比 Table 1 Curvature radius comparison of transverse and longitudinal section line

这与调形精度、试验操作误差、轧辊的回弹等因素有关, 因此, 柔性轧制成形方法可得到成形效果比较好的曲面零件。

(1)分析了柔性轧制成形三维曲面的变形机制和应力应变规律。从辊缝函数与板料厚度的关系出发, 给出了板料横向上任意点的纵向纤维长度公式。

(2)建立了有限元模型, 并对成形过程进行了数值模拟, 得出了曲面柔性轧制成形规律, 不论成形凸曲面还是鞍曲面:横向曲率半径不变时, 纵向曲率半径与压下率成反比; 压下率不变时, 横向曲率半径与纵向曲率半径成反比。

(3)进行了成形试验, 轧制成形了两种曲面件, 柔性轧制成形方法可以得到预期的三维曲面。