作者简介:胡侃(1974-),男,在站博士后.研究方向:金属热冲压材料,汽车工程,机械工程.E-mail:kanhu0808@163.com
基于新型混合动力校车安全性和轻量化的需求,根据侧围立柱结构主要承受弯曲冲击载荷的特点,同时结合热冲压高强钢的性能优势,提出了一种热冲压立柱结构。对悬臂梁中部承受的冲击载荷进行有限元计算分析,结果表明:在质量不变的情况下,热冲压立柱结构的最大变形量降低了74.9%,承载能力提高了223.6%,具有突出的抗碰撞性能和轻量化潜力。通过整车侧翻有限元计算,并结合全尺寸实车侧翻试验验证了有限元计算结果的准确性。基于径向基函数建立了热冲压立柱截面尺寸与侧翻碰撞变形量、加速度以及结构质量的代理模型,采用遗传算法求解校车结构侧翻碰撞安全性和轻量化的多目标优化问题,结果显示:变形量平均降低了38.2%,生存空间加速度降低了23.4%,同时结构质量降低了63.9%,进一步表明热冲压立柱结构可以同时大幅度提高侧翻安全性和轻量化性能。
A novel hot-stamping beam with ultra-high strength is introduced to improve both rollover safety and lightweight performance, which is based on the mechanical characteristics of the side beams and the excellent properties of hot-stamping material. Finite Element Method (FEM) analysis is used to calculate single cantilever beam with impact load on the middle position. Results show that the maximum deformation of the hot-stamping beam is about 74.9% lower the load bearing capacity is about 223.6% higher than that with equal-mass. This demonstrates that this novel beam has extremely crashworthy performance and potency of lightweight. The rollover crash simulation and test of the original school bus are conducted, which show that the simulation result is in good agreement with the test result, suggesting that the FEM analysis is accurate. The deformation, acceleration and structure weight surrogate are established based on Radial Basis Function (RBF) method. Then, multi-objective evolutionary algorithms are employed to obtain the optimal solution set. The results show that the deformation is decreased by 38.2%, the acceleration of survive room is decreased by 23.4% and the structure weight is reduced by 63.9%. It is proved that the hot-stamping steel beam performs far better in both rollover safety and lightweight performance compared to the original one.
校车安全问题一直受到研究者的广泛关注。其中侧翻碰撞是校车及客车最严重的事故形式, 通常会造成很严重的伤亡[1, 2]。在侧翻碰撞过程中, 侧围立柱及顶围横梁构成的封闭环结构是抵抗变形最为重要的结构。姜勇等[3]提出了泡沫铝侧围吸能结构, 可以降低最大碰撞加速度达29%, 减少了客车侧翻碰撞能量对乘员的损伤。刘玉等[4]根据客车侧围立柱在侧翻碰撞中所受力矩不同, 提出了变截面的冲压立柱结构, 在质量相同的情况下对比原始矩形梁立柱, 变形量降低了近48.8%。然而, 目前针对提高校车侧翻安全的研究工作较少, 而大型校车由于整备质量较高, 安全性要求也非常高, 因此急需一种有效的解决方式来大幅度提高校车的侧翻安全性。近几年, 热冲压高强钢由于具有超高的屈服强度和抗拉强度, 同时具有高的成形性、碰撞吸能性、疲劳强度和轻量化表现等优势, 被广泛应用于汽车加强梁、B柱及防撞梁等承载和抗冲击的零部件中, 以提高车辆在碰撞过程中的抗变形能力[5, 6]。
本文根据侧翻碰撞中, 侧围立柱主要承受弯曲冲击载荷的特点, 结合热冲压高强钢的性能优势, 提出一种新型校车热冲压立柱结构。单一结构承载和整车侧翻碰撞有限元计算结果表明, 该结构相对于传统结构可以提高抗碰撞变形能力、吸能性以及轻量化表现。最后, 通过多目标优化方法对热冲压立柱截面尺寸进行最优设计, 结果表明, 热冲压立柱结构可以大幅度降低碰撞变形量、碰撞加速度以及结构质量。
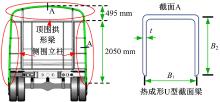
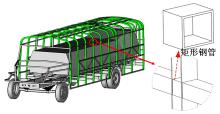
本文提出采用热冲压U型校车立柱结构替换原始侧围立柱和顶围拱形梁, 通过焊接连接, 如图1所示, 图中, t、B1、B2分别为U型截面梁的厚度、宽度和高度。根据封闭环结构在侧翻碰撞时的受力情况(见图2), 车体经翻转与地面接触碰撞时受到地面反力F, 其分量为F1和F2。F2对侧围立柱产生弯矩和剪切力, 导致侧围立柱的弯曲变形以及剪切变形; F对顶围拱形梁产生弯矩, 导致其同样产生弯曲变形和剪切变形, 其中F2对侧围立柱的弯矩更大, 它是导致侧围立柱变形的主要原因。因此基于热冲压U型立柱结构的性能特点, 通过增大材料强度来提高最大承载能力, 减小变形量, 同时U型截面梁具有材料利用率高的特点, 可以适当降低结构质量。
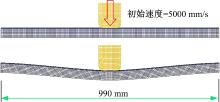
侧围立柱同时承受弯矩和剪切力, 可以近似等效为悬臂梁中部承受冲击载荷的受力形式, 如图3所示。其中冲击载荷可以等效为刚性质量块附加初始速度来模拟, 初始速度定义为5000 mm/s, 质量块质量为100 kg。热冲压高强钢及传统结构材料参数经金属单向拉伸标准试验测得, 如表1所示。采用有限元计算软件LS-DYNA分别计算Q235钢的2.5 mm厚度传统矩形截面梁和不同厚度的热冲压高强钢U型截面梁的冲击模拟, 其中截面尺寸B1=50, B2=40。3.29 mm厚度的U型截面梁的质量与2.5 mm厚度矩形截面梁一致。
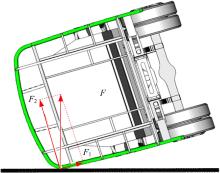 | 图2 侧翻碰撞过程中校车侧围结构受力示意图Fig.2 Schematic diagram of force analysis of school bus side structures when rollover crash |
| 表1 材料参数 Table 1 Material parameters |
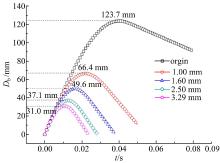
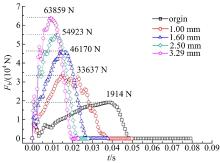
图4为悬臂梁中部挠度随时间变化曲线。图5为质量块所受反力随时间变化曲线。从图4和图5可以看出:①热冲压立柱结构中部挠度远小于传统结构, 质量相同的情况下, 挠度为31 mm, 降低了74.9%, 厚度最薄的1.0 mm热冲压立柱结构挠度也几乎是传统结构的一半, 证明该新型结构抵抗冲击变形的能力远优于Q235钢矩形截面梁。②质量块反力峰值力大小反映了梁承载能力, 质量相同的情况下, 承载能力提高了233.6%, 热冲压高强钢U型截面梁的承载能力远大于传统Q235钢矩形截面梁。
虽然热冲压U型截面梁在上述方面具有突出的优势, 但是U型截面梁结构在横向受力时的刚度偏弱, 尤其是其与前进方向梁的连接处, 在紧急制动或加速时会有局部变形, 故此处应该加强以提高局部刚度。将矩形钢管切割成合适尺寸后, 填充在U型截面梁立柱中, 且与两边横向梁的位置对应, 并通过焊接与U型截面梁连接, 如图6所示。
根据ECE R66标准中侧翻试验规定以及某油电混合动力校车原型, 建立校车有限元模型, 如图7所示。其中包括车架、底盘、蒙皮等主要部件, 其他配件(如电机、电池等)则以刚体附加配重的形式表示, 保障整车质心位置与原型车相符。整个模型约有186 000个单元, 192 000个节点。对于各个变形体部件的连接采用一维刚性体连接。
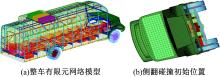 | 图7 校车整车有限元网格模型及侧翻碰撞初始位置Fig.7 Element model of school bus structure and initial position of rollover crash |
建立刚性墙地面, 并设置地面与校车的接触以及车身结构自身的自接触。为便于考虑整车自重的影响, 设置重力加速度。为节省运算时间, 模型直接计算校车与地面碰撞初始时刻(见图7(b)), 根据校车倾倒时刻和跌落时刻的重心位置及整车尺寸参数, 通过能量守恒定律计算出碰撞时刻的初始角速度为2.387 rad/s。
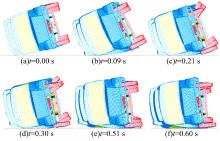
采用有限元计算软件LS-DYNA计算整个侧翻碰撞过程, 整个过程历时0.6 s, 包括初始碰撞、变形最大和变形回弹3个过程, 其中0.2 s左右是整体变形最大时刻, 如图8所示。
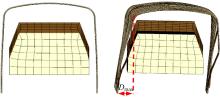
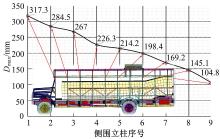
根据安全性评价标准以及有限元计算结果可知, 校车侧围结构并没有侵入到生存空间内部, 证明原始校车结构的侧翻碰撞安全性是合格的。为了方便后续定量研究侧翻碰撞安全性, 本文引入以下几种定量指标:①侧围立柱变形量最大值Dmax, 如图9所示, 它反映了侧围立柱结构最大变形程度, 其值越小表明侧围结构越难以侵入生存空间。②生存空间合成加速度A, 在碰撞过程中, 它使车内乘员受到冲击响应, 会对车内乘员造成伤害, 其值越小表明乘员受到伤害越低。③梁截面面积S, 其值越小表示重量越轻。据此, 原始校车侧翻碰撞时的立柱变形量如图10所示。原始校车侧翻碰撞安全性指标如下:B1=50 mm; B2=40 mm; t=2.0 mm; Dmax=317.3 mm; A=6.52× 104 mm/s2; S=360 mm2。
通过整车侧翻实车试验(见图11)来对比验证有限元分析结果的可靠性, 通过在车内预装变形规来测量侧翻过程中侧围立柱的变形量, 本次试验在第2、5、8根立柱处布置了变形规, 具体试验结果如表2所示。三根立柱变形量误差都在10%以内, 且变形量变化趋势一致, 变形量平均值误差只有3%, 证明实车试验结果与有限元结果基本一致, 趋势相符, 侧翻碰撞的有限元分析方法是准确的, 因此后续研究将基于有限元分析的结果。
| 表2 校车侧翻试验中的侧围立柱变形量 Table 2 Deformation of side beams in school bus rollover crash test mm |
为了探究热冲压高强钢U型梁的轻量化安全性潜力, 通过多目标优化设计, 找出最优的U型截面尺寸B1、B2和t, 同时基于径向基函数法得出U型截面的各个尺寸对于碰撞安全性的影响趋势。
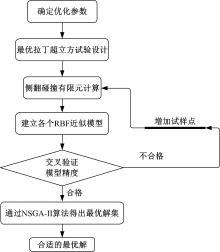
传统多目标优化方法是基于响应曲面法建立设计变量对于目标函数的关系, 并通过一定的优化计算方法找出最佳设计参数, 对于单一结构或者简单工况下的模型适用性较好, 但针对高度非线性问题或复杂工况下的模型精度较差。故本文基于径向基函数法[7]建立U型截面尺寸与轻量化安全性指标的代理模型, 通过改进非支配排序遗传算法(NSGA-Ⅱ )[8]求解出最佳设计变量。图12为本文优化方法流程图。
根据高强度钢板的热冲压性和校车可装配性来考虑U型梁的截面尺寸范围, 通过最优拉丁超立方试验设计[9]来设计试验样本点空间。对样本点进行侧翻碰撞仿真计算并提取有关侧翻碰撞安全评价的定量指标, 如表3所示。
| 表3 试验设计样本点及定量指标 Table 3 Sample points and indexes of experiment design for simulation |
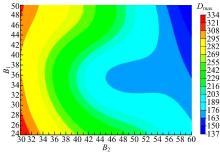
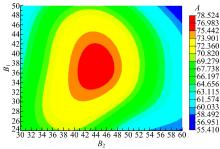
根据仿真数据建立截面尺寸关于侧围立柱平均变形量、生存空间合成加速度以及U型梁截面面积的径向基函数近似模型。通过交叉验证法来验证这些近似模型的可靠性及精度。图13为1.6 mm厚度下B1和B2关于Dmax的径向基函数近似模型云图。从图中可以看出:当B2小于54 mm时, 随着B1的增大, Dmax呈现先减小再增大的趋势, 但是当B2大于54 mm时, Dmax随着B1的增大而减小。图14为1.6 mm厚度下B1和B2关于A的径向基函数近似模型云图。从图中可以看出中间高、四周小的整体趋势。
综上, 通过径向基函数近似模型可以知道设计参数是如何影响目标函数的, 因此, 基于这些径向基函数近似模型可以采用优化算法找出最优设计变量组合。
为了求解出最优的梁截面尺寸, 将B1、B2和t等作为设计变量, 同时考虑侧翻碰撞安全性和轻量化性能, 即以Dmax、A以及S作为目标函数, 该优化问题的表达式如式(1)所示:
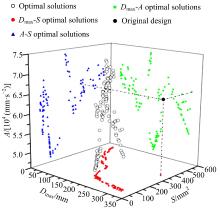
以Dmax、A以及S三个径向基函数近似模型为基础, 采用NSGA-Ⅱ 算法, 经过50代计算, 得出一系列优化解集, 如图15所示。图中还包括该解集在各个坐标平面的投影点, 可以分别看出每组定量指标的趋势, 比如Dmax-S(图15中红色圆形实心点表示)的基本趋势是随着S的降低, Dmax逐渐增大, 当S低于104 mm2时, Dmax迅速增大, 不利于侧翻安全性。从A-S(图15中蓝色三角形实心点表示)投影点中可以看出, S达到135 mm2左右, A趋于最小值, 此时是最佳的设计点, S增大或减小, A都会迅速增大, 不利于侧翻安全性。因此, 根据图15以及各个指标间的关系, 很容易找出最合适的设计点应该在S取115~135时, 对应的设计点解集如表4所示, 其中0#点代表原始校车的结果。
| 表4 优化后的设计点及定量指标 Table 4 Sample points and indexes after optimization |
基于表5的设计点, 为了减少成形难度, 去掉高宽比大的设计点, 综合考虑安全性和轻量化表现, 本文选择11#设计点作为最终的设计结果, 对比原始设计点, 最终优化结果中侧围立柱变形量平均值降低了38.2%, 生存空间加速度降低了23.4%, 同时截面面积降低了63.9%, 即196.9 kg, 轻量化及侧翻碰撞安全性提高效果显著。
根据侧翻碰撞时侧围立柱主要承受弯曲冲击载荷的特点, 基于热冲压高强钢的性能优势在校车车身结构中引入热冲压U型立柱结构, 通过单一结构承载和整车侧翻碰撞两种工况分析了该结构的性能。悬臂梁中部受冲击载荷有限元计算结果表明:相对于传统梁结构, 在质量不变的情况下, 热冲压立柱结构的最大变形量降低了74.9%, 承载能力提高了223.6%, 具有突出的抗碰撞性能和潜在的轻量化特性。基于径向基函数建立了热冲压立柱截面尺寸B1、B2和t与侧翻变形量、侧翻碰撞加速度以及结构质量的代理模型, 经过多目标优化, 结果显示变形量平均值降低了38.2%, 生存空间加速度降低了23.4%, 同时截面面积降低了63.9%, 进一步表明热冲压立柱结构可以同时大幅度提高侧翻安全性和轻量化表现。基于径向基函数法可以有效建立梁截面尺寸与侧翻碰撞结果的高度非线性代理模型, 表明该方法是一种非常高效的结构设计手段。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| 3 |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|