转矩波动下电动轮系统机电耦合振动特性

引用本文

毛钰, 左曙光, 林福. 转矩波动下电动轮系统机电耦合振动特性. 吉林大学学报(工学版), 2017, 47(3): 908-916
MAO Yu, ZUO Shu-guang, LIN Fu. Electromechanical coupled vibration characteristics of electric wheel under torque ripple. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 908-916 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703030
Permissions

转矩波动下电动轮系统机电耦合振动特性

毛钰, 左曙光, 林福

同济大学新能源汽车工程中心,上海 201804

左曙光(1968-),男,教授,博士生导师.研究方向:汽车系统动力学与控制.E-mail:sgzuo@tongji.edu.cn

作者简介:毛钰(1992-),男,博士研究生.研究方向:电动轮系统振动与控制.E-mail:maoyu1224@163.com

基金项目:国家自然科学基金项目(51375343); 上海市教委科研创新项目(15ZZ015)

摘要

针对转矩波动下电动轮系统机电耦合振动问题,推导了 d/q轴坐标系下考虑永磁体磁场谐波的永磁同步电机电磁转矩数学模型以反映轮毂电机转矩波动特征。基于电动轮扭转和纵向耦合振动方程分析了电动轮系统固有特性,考虑电流闭环的影响,并集成转矩模型和振动方程建立了电动轮系统机电耦合模型。基于机电耦合模型分析了耦合对转矩波动和系统振动特性的影响规律,结果表明:电机转子的转速波动在电动轮旋转模态频率处会对电机转矩波动产生负反馈削弱效果;机电耦合主要会改变电动轮耦合系统第三阶模态阻尼比进而影响振动特性,而且阻尼比随磁链的增加而线性增加,随电感的增加而下降直至趋于稳定。因此,合理选取轮毂电机电磁参数对抑制电动轮系统振动有一定的意义。

关键词: 自动控制技术; 车辆工程; 转矩波动; 电动轮系统; 机电耦合振动; 模态阻尼比

中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2017)03-0908-09

Electromechanical coupled vibration characteristics of electric wheel under torque ripple

MAO Yu, ZUO Shu-guang, LIN Fu

Clean Energy Automotive Engineering Center, Tongji University, Shanghai 201804, China

Abstract

In view of the electromechanical-coupled vibration problem of electric wheel, the electromagnetic torque of permanent magnet synchronous motor is derived in taking account the effects of space harmonics of the permanent magnetic field. Then, based on the equations of coupled torsional and horizontal vibration, the inherent characteristics of the electric wheel system are analyzed. The electromechanical-coupled vibration model of the electric wheel is established by introducing closed-loop control of d/q axis current and combining the electromagnetic torque model and vibration equations. Based on this model the influence rules of electromechanical coupling effects on torque ripple and vibration performance are studied. Results show that the speed fluctuation of the rotor arising from torque ripple will in turn exert an effect of weakening on the torque ripple, especially at the rotating modal resonant operating condition of the electric wheel. The third modal damping ratio of the electric wheel coupling system is evidently influenced by the electromechanical coupling effects and varies with electromagnetic parameters, among which the magnet flux linkage has the largest impact.

Key words: automatic control technology; vehicle engineering; torque ripple; electric wheel system; electromechanical coupled vibration; modal damping ratio

Show Figures

0 引言

轮毂电机驱动电动汽车以其在车辆总体结构布置、底盘主动控制以及操纵性等方面的明显优势成为未来电动汽车的发展方向, 其关键部件之一的电动轮系统也因此成为开发研究的核心^{[1, 2, 3]}。电动轮系统是由轮毂电机和轮胎总成构成的机电耦合系统, 轮毂电机的电磁激励与轮胎等复杂弹性结构的相互作用引起电动轮系统不同于传统轮胎-悬架系统的机电耦合动力学问题。

清华大学Song^[4]和Li^[5]等分析了轮毂电机驱动下轮胎的扭转振动、滑移率及纵向力波动等现象, 并指出上述动力学行为由轮毂电机电磁转矩和轮胎弹性结构耦合作用引起。左曙光等^[6]进一步通过电动轮台架试验发现了轮毂电机转矩波动引起的电动轮-悬架系统的阶次振动, 并分析了电机转速和负载转矩等参数对振动的影响。上述文献对电动轮系统电磁激励下的动力学问题进行了研究, 着重揭示了轮毂电机转矩波动下的电动轮机电耦合振动问题, 但缺乏对机电耦合影响机理的深入分析。

在电机系统的机电耦合影响机理研究方面, 陈贵清^[7]和徐进友^[8]等分析了电磁激励作用下水轮发电机组转子轴系的机电耦合扭转振动特性, 指出由于受到电磁约束作用, 振动系统会出现零阶固有频率, 受时变电磁刚度的影响, 系统稳态响应对电磁参数变化敏感。文献[7, 8]揭示了发电机运用场合下的机电耦合影响机理, 但由于电动机驱动系统存在电流闭环控制等因素的影响, 其耦合影响规律表现出不同的特征, 有待深入分析。Liu^[9]和Chen^[10]等先后针对异步电机和永磁同步电机驱动机电耦合系统的分叉和混沌等非线性特征进行了研究, 但同样基于开环仿真无法反映定子电流的影响, 而且文中基于简单的两自由度扭振模型未能真实反映电动机驱动系统动力学特征, 尤其不适用于电动轮振动复杂的系统。

本文首先建立了电动轮机电耦合振动模型, 模型由考虑转子磁场谐波的永磁同步电机电流闭环控制系统和反映电动轮扭转和纵向耦合振动的动力学系统构成, 能够真实反映电机转矩波动特征及多自由度电动轮系统模态特征和固有特性。其次, 基于机电耦合模型分析了转矩波动变化规律, 揭示了电动轮动力学特征对转矩波动的耦合影响机理。最后, 考虑转矩激励与电动轮运动学参数的关联研究了电磁因素对电动轮耦合系统模态特征及固有特性的影响, 进而分析了电动轮系统机电耦合振动特性。

1 电动轮系统机电耦合模型

1.1 考虑永磁体磁场谐波的电机数学模型

永磁同步电机理想模型假设永磁体磁场在气隙中呈现正弦分布, 但实际上由于永磁体磁极受制造及工艺上的限制, 气隙中永磁体磁场在空间并不呈理想正弦分布而是存在一定的谐波^[11], 进而使永磁体在三相绕组中感应的磁链存在谐波, 可表示为:

$\begin{matrix} [\begin{matrix} ψ_{mA} \\ ψ_{mB} \\ ψ_{mC} \end{matrix}] = [\begin{matrix} \overset{\infty}{\sum_{i = 1}} ψ_{2 i - 1} [(2 i - 1) pθ] \\ \overset{\infty}{\sum_{i = 1}} ψ_{2 i - 1} [(2 i - 1) (pθ - \frac{2}{3} π)] \\ \overset{\infty}{\sum_{i = 1}} ψ_{2 i - 1} [(2 i - 1) (pθ + \frac{2}{3} π)] \end{matrix}] \end{matrix}$ （1）

式中:ψ _mA(ψ _mB、ψ _mC)为A(B、C)相磁链; ψ ₂_i-₁为空间(2i-1)p阶磁场产生的定子磁链幅值。

经Clark和Park变换可确定在d/q轴坐标系下, 永磁体磁场产生的d、q轴磁链为:

$\begin{matrix} \{\begin{matrix} ψ_{d} = ψ_{1} + \overset{\infty}{\sum_{i = 1}} (ψ_{6 i - 1} + ψ_{6 i + 1}) \cos 6 ipθ \\ ψ_{q} = \overset{\infty}{\sum_{i = 1}} (- ψ_{6 i - 1} + ψ_{6 i + 1}) \sin 6 ipθ \end{matrix} \end{matrix}$ （2）

由式(2)可知, 不同于线性模型, 考虑永磁体磁场非正弦分布后, d、q轴磁链中出现了相对空间位置的6ip次波动, 将波动项记为:

$\begin{matrix} \{\begin{matrix} ψ_{d_ripple} = \overset{\infty}{\sum_{i = 1}} (ψ_{6 i - 1} + ψ_{6 i + 1}) \cos 6 ipθ \\ ψ_{q_ripple} = \overset{\infty}{\sum_{i = 1}} (- ψ_{6 i - 1} + ψ_{6 i + 1}) \sin 6 ipθ \end{matrix} \end{matrix}$ （3）

结合磁链表达式, 并由定子绕组电压平衡关系和转矩方程可以确定考虑永磁体磁场谐波时d/q轴坐标系下电机数学模型为^[12]:

$\begin{matrix} \{\begin{matrix} u_{d} = R i_{d} + L_{d} \frac{d}{dt} i_{d} - pω L_{q} i_{q} + \\ \frac{d ψ_{d_ripple}}{dt} - pω ψ_{q_ripple} \\ u_{q} = R i_{q} + L_{q} \frac{d}{dt} i_{q} + p ω L_{d} i_{d} + pω ψ_{1} + \\ \frac{d ψ_{q_ripple}}{dt} + pω ψ_{d_ripple} \\ T_{e} = 1.5 p {ψ_{1} i_{q} + (L_{d} - L_{q}) i_{d} i_{q} - \\ \overset{\infty}{\sum_{i = 1}} {[(6 i - 1) ψ_{6 i - 1} + \\ (6 i + 1) ψ_{6 i + 1}] i_{d} \sin 6 ipθ} + \\ \overset{\infty}{\sum_{i = 1}} {[- (6 i - 1) ψ_{6 i - 1} + \\ (6 i + 1) ψ_{6 i + 1}] i_{q} \cos 6 ipθ}} \end{matrix} \end{matrix}$ （4）

式中:u_d、u_q分别为d、q轴电压; i_d、i_q分别为d、q轴电流; L_d、L_q分别为d、q轴电感; R为定子相电阻; ω =dθ /dt为转子旋转角速度; T_e为电磁转矩。

本文针对某一具体外转子表贴式永磁同步轮毂电机进行研究, 相关参数如表1所示。关于电机极槽配合、绕组结构等关键设计参数对谐波转矩的影响不是本文的研究重点, 相关研究可参考文献[13, 14]。

表1 永磁同步电机参数 Table 1 Parameters of PMSM

1.2 电动轮系统动力学建模及固有特性分析

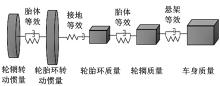
由前期研究可知^[15], 轮毂电机转矩波动主要引起电动轮系统扭转和纵向振动, 因此, 本文考虑轮胎弹性动力学特征, 建立包括轮胎和轮辋/电机等质量的扭转和纵向平移自由度的振动模型:轮胎和轮辋/电机通过胎侧连接, 将其等效为扭转刚度和纵向平移刚度; 轮辋经悬架摆臂及衬套与车身在纵向连接; 轮胎扭转自由度和纵向平移自由度通过考虑轮胎松弛特性的瞬态刷子模型实现耦合。该模型对于反映轮毂电机转矩波动下电动轮振动特性的适用性已通过台架试验得到验证^[15]。电动轮振动系统示意图如图1所示。

	Figure Option View Download New Window
	图1 电动轮振动系统示意图Fig.1 Schematic of vibration system of electric wheel

电动振动系统动力学方程如下所示:

$\begin{matrix} \{\begin{matrix} I_{dy} \frac{d^{2} θ}{d t^{2}} + c_{bθ} (ω - \frac{d θ_{b}}{dt}) + k_{bθ} (θ - θ_{b}) = T_{e} \\ I_{by} \frac{d^{2} θ_{b}}{d t^{2}} + c_{bθ} (\frac{d θ_{b}}{dt} - \frac{d θ_{d}}{dt}) + k_{bθ} (θ_{b} - θ_{d}) = - R_{e} F_{cx} \\ m_{b} \frac{d^{2} x_{b}}{d t^{2}} + c_{b} (\frac{d x_{b}}{dt} - \frac{d x_{a}}{dt}) + k_{b} (x_{b} - x_{a}) = F_{cx} \\ m_{a} \frac{d^{2} x_{a}}{d t^{2}} + c_{b} (\frac{d x_{a}}{dt} - \frac{d x_{b}}{dt}) + k_{b} (x_{a} - x_{b}) + \\ c_{ux} (\frac{d x_{a}}{dt} - \frac{d x_{u}}{dt}) + k_{ux} (x_{a} - x_{u}) = 0 \\ m_{u} \frac{d^{2} x_{u}}{d t^{2}} + c_{ux} (\frac{d x_{u}}{dt} - \frac{d x_{a}}{dt}) + k_{ux} (x_{u} - x_{a}) = F_{d} \\ \frac{d F_{cx}}{dt} \frac{1}{k_{c}} + F_{cx} \frac{1}{c_{c}} = \frac{d θ_{b}}{dt} R_{e} - \frac{d x_{b}}{dt} \end{matrix} \end{matrix}$ （5）

式中:x_b、x_a分别为轮胎和轮辋/电机的纵向位移; θ _b为轮胎旋转角; F_cx为轮胎纵向力; F_d为车身受到的阻力; R_e为轮胎半径; m_b、m_a、m_u分别为轮胎、轮辋/电机和车身的质量; I_by、I_dy分别为轮胎和车轮的转动惯量; k_b、c_b分别为轮胎平移刚度和平移阻尼; k_bθ、c_bθ分别为轮胎旋转刚度和旋转阻尼; k_ux、c_ux分别为悬架衬套刚度和衬套阻尼; k_c为胎面纵向刚度; c_c为胎面纵向阻尼。

电动轮模型参数为:m_b=6 kg; m_a=26 kg; m_u=300 kg; c_ux=1273.9 Ns/m; k_b=2.588× 10⁶ N/m; c_b=536 Ns/m; I_by=0.7 kg· m²; I_ay=0.4 kg· m²; k_bθ=8.2688× 10⁴ N/m; c_bθ=17 Nms/rad; R_e=0.3044 m; k_c=1.065× 10⁶ N/m; k_ux=26232 N/m; c_c=1.18× 10⁵ Ns/m。

根据线性系统理论可以确定系统固有频率及阻尼比如表2所示。

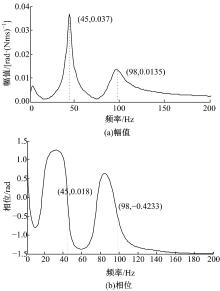
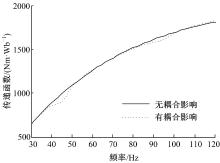
由式(4)(5)可知, 电动轮系统主要通过电磁转矩和转子运动学参数实现机电耦合, 为便于后续分析, 确定电动轮系统电机转子角速度响应相对电机转矩激励的传递函数(即系统机械导纳)如图2所示。由于共振的影响, 电动轮系统的三、四阶旋转模态处机械导纳较大, 而且在此时, 机械导纳相位在0左右, 即转矩激励和转速响应在共振时相位比较接近, 这是因为振动系统共振时, 激励力主要用于平衡系统阻尼力。

表2 电动轮模态参数 Table 2 Modal parameters of electric wheel

	Figure Option View Download New Window
	图2 电动轮系统机械导纳Fig.2 Mechanical admittance of electric wheel system

1.3 电机闭环控制及电动轮机电耦合系统

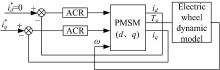
为实现对轮毂电机实时运行工况下电磁转矩的模拟, 建立永磁同步电机闭环控制系统。对于轮毂电机驱动控制系统, 一般不存在速度和位移闭环^{[4, 5]}, 因此本文采用d/q轴电流单闭环控制系统进行简化。另外, 研究所针对的电机工作范围为恒转矩区, 采用最大电流比(MTPA)控制(对于表贴式电机, i_d=0), 本文未针对采用弱磁控制的恒功率区的机电耦合特性进行研究。d/q轴电流采用PI调节器进行控制, PI调节器系统传递函数为:

$\begin{matrix} H_{ACR} (s) = k_{p} \frac{τ_{c} s + 1}{τ_{c} s} \end{matrix}$ （6）

式中:H_ACR(s)为电流调节器传递函数; k_p为调节器比例系数; τ _c为调节器积分时间常数。

由于控制系统中, 调制算法和开关动作等因素引起的转矩波动频率较高, 对电动轮系统振动特性影响较小, 在模型中忽略变频器调制算法及逆变器开关特性的影响。结合电机本体数学模型得到轮毂电机闭环模型如图3所示。图中, $\begin{matrix} i_{d}^{*} \end{matrix}$ 、 $\begin{matrix} i_{q}^{*} \end{matrix}$ 分别为d轴、q轴电流参考值; ω 为转子旋转角速度。由于考虑了永磁体磁场谐波分量, 该模型能够反映电磁转矩的波动特征。

	Figure Option View Download New Window
	图3 轮毂电机闭环模型Fig.3 Closed loop model of in-wheel motor

根据文献[16]中设计原则确定k_p=0.35, τ _c=0.0083。另外, 可确定电流闭环时间常数为T=L_q/k_p=0.002。

电动轮振动系统通过轮毂电机电磁转矩与电动轮动力学系统的相互作用构成了一个机电耦合系统, 在轮毂电机闭环模型基础上, 考虑电动轮系统动力学结构的影响, 得到电动轮系统机电耦合模型如图4所示。

	Figure Option View Download New Window
	图4 电动轮系统机电耦合模型Fig.4 Electromechanical model of electric wheel system

2 机电耦合对转矩波动的影响分析

由电动轮机电耦合模型可知, 电机电磁转矩(包含波动特征)受到转子运动学参数(转速、转角)的影响, 而转矩波动作为电动轮振动系统的激励会引起包含电机转子在内的动力学系统运动学参数的改变, 进而影响转矩波动特征。为了分析转矩波动下电动轮系统的机电耦合振动特性, 需研究机电耦合对转矩波动的影响规律及其机理。

2.1 机电耦合对转矩波动的影响规律分析

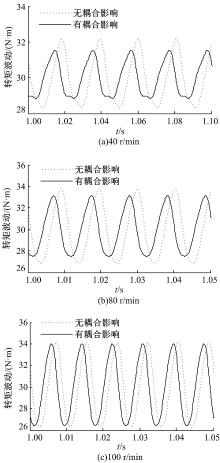
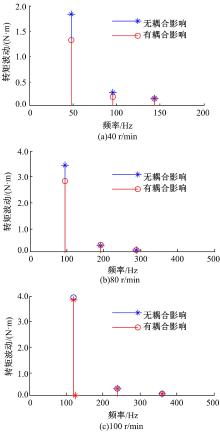
针对图3中所描述的轮毂电机闭环模型(无耦合影响)和图4中所描述的电动轮系统机电耦合模型, 设定轮毂电机目标转矩为30 N· m(对应q轴电流为19.6 A), 转速分别为40、80和100 r/min时, 二者转矩输出情况如图5和图6所示。可以看出:①电磁转矩中存在波动成分, 而且其波动频率为转动频率的6pk倍(p为电机极对数, k=1, 2, 3, …), 该波动成分来源于气隙中永磁体磁场空间谐波; ②考虑电动轮动力学特性影响时, 转矩波动频率特征没有发生改变, 但转矩波动幅值相对不考虑机电耦合影响时有所下降, 而且在40和80 r/min时下降较100 r/min时明显。

	Figure Option View Download New Window
	图5 转矩波动的时域对比Fig.5 Contrast of torque ripple in time domain

	Figure Option View Download New Window
	图6 转矩波动的频域对比Fig.6 Contrast of torque ripple in frequency domain

	Figure Option View Download New Window
	图7 加速工况下的转矩波动对比Fig.7 Contrast of torque ripple in time domain under acceleration condition

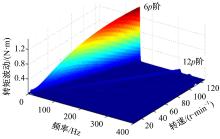
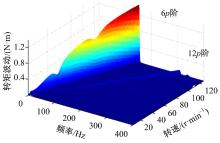
为了分析电动轮机电耦合对转矩波动影响的一般规律, 设定轮毂电机运行于目标转矩为30 N· m(对应q轴电流为19.6 A), 转速为0~130 r/min的加速工况下, 从而遍历电动轮系统振动分析所关注的频段范围。图7为转矩波动时间历程的对比, 在9 s和18 s处(对应转速为40和80 r/min), 有耦合影响下的转矩波动量相对无耦合影响时有一定的降低。图8和图9分别为无耦合影响及有耦合影响下的转矩波动时频图, 二者体现出的阶次主要为6p、12p、18p, 其中6p阶为最主要阶次, 转矩的区别也主要体现在6p阶波动上, 因此提取转矩波动6p阶次切片如图10所示, 有耦合影响相对无耦合影响下的转矩波动量下降主要表现在频率为48 Hz和96 Hz处, 对应表2中车轮和轮胎同向、反向旋转的模态频率, 即电动轮机电耦合对轮毂电机转矩波动的削弱影响主要体现在系统旋转模态频率处。

	Figure Option View Download New Window
	图8 无耦合影响下的转矩波动时频图Fig.8 Time frequency map of torque ripple without coupling effects

	Figure Option View Download New Window
	图9 有耦合影响下的转矩波动时频图Fig.9 Time frequency map of torque ripple with coupling effects

	Figure Option View Download New Window
	图10 6p阶转矩波动对比Fig.10 Contrast of 6p order torque ripple

2.2 机电耦合对转矩波动的影响机理分析

为便于分析机电耦合机理, 将永磁同步电机数学模型进行合理简化:①因电机控制采取i_d=0的策略, 而且电磁转矩主要取决于q轴电流, 因此分析时忽略d轴电流的影响; ②因永磁体基波磁链远大于谐波磁链, 因此仅在电压方程中考虑磁链谐波的影响, 而在电磁转矩方程中忽略谐波磁链对应项。基于上述假设, 电动轮机电耦合方程可简化为:

$\begin{matrix} \{\begin{matrix} u_{q} (s) = H_{ACR} (s) (i_{q}^{*} (s) - i_{q} (s)) \\ R i_{q} + L_{q} \frac{d}{dt} i_{q} = u_{q} - pω ψ_{1} - \frac{d}{dt} ψ_{q_ripple} \\ T_{e} = K_{t} i_{q} \\ ω (s) = H_{admit} (s) T_{e} (s) \end{matrix} \end{matrix}$ （7）

式中:R为电机定子相电阻; H_admit(· )为电动轮系统机械导纳, 由1.2节中方法确定; K_t=1.5pψ ₁为转矩系数。

由式(7)可知, 转矩波动作用于电动轮系统, 主要通过引起电机转子的转速波动, 改变定子感应电动势谐波及电流谐波, 从而影响转矩波动。电动轮系统的动力学特征对上述耦合作用产生影响:①在电动轮系统共振时, 电机转矩波动引起的转速波动明显增大, 耦合影响加强, 而且旋转模态对电机转速波动贡献较大(见图2(a)), 因此电动轮机电耦合对转矩波动的影响主要体现在系统旋转模态频率处; ②对于电动轮振动系统, 在模态频率处, 电机转矩与电机转速相位接近(见图2(b)), 因此图4中转速将对电流及转矩波动形成负反馈, 使机电耦合对转矩波动的影响表现为削弱作用。

为验证上述分析, 由式(7)确定以磁链谐波为输入、转矩为输出的耦合系统传递函数。另外, 为形成对比, 忽略式(7)中第4个表达式同样确定无耦合时系统传递函数:

$\begin{matrix} \{\begin{matrix} H_{uncoupled} (s) = \frac{T_{e} (s)}{ψ_{q_ripple} (s)} = - \frac{K_{t} T S^{2}}{(TS + 1) (L_{q} S + R)} \\ H_{coupled} (s) = \frac{T_{e} (s)}{ψ_{q_ripple} (s)} = - K_{t} T S^{2} \times \\ [(TS + 1) (L_{q} S + R) (1 + A {(s))]}^{- 1} \\ A (s) = \frac{p K_{t} T ψ_{1} S}{(TS + 1) (L_{q} S + R)} H_{admit} (s) \end{matrix} \end{matrix}$ （8）

式中:H_uncoupled(· )为无耦合时由磁链波动到转矩波动系统传递函数; H_coupled(· )为耦合时由磁链波动到转矩波动系统传递函数; S为拉普拉斯算子。

基于上述分析, 在共振处, |1+A(s)|> 1, 所以 $\begin{matrix} |H_{uncoupled} (s)| \end{matrix}$ > $\begin{matrix} |H_{coupled} (s)| \end{matrix}$ , 如图11所示。

	Figure Option View Download New Window
	图11 磁链谐波到转矩波动传递函数对比Fig.11 Contrast of transfer function from flux ripple to torque ripple

3 机电耦合影响的电动轮振动特性

考虑电机的电磁转矩特征将电动轮动力学方程式(5)中第一个表达式可改写为:

$\begin{matrix} \{\begin{matrix} I_{dy} \frac{d^{2} θ}{d t^{2}} + c_{bθ} (ω - \frac{d θ_{b}}{dt}) + k_{bθ} (θ - θ_{b}) - \\ T_{e 1} (θ, ω) = T_{e 0} \\ \frac{R}{1.5 p ψ_{1}} T_{e 0} + \frac{L_{q}}{1.5 p ψ_{1}} \frac{d}{dt} T_{e 0} = \\ u_{q} - \frac{d}{dt} ψ_{q_ripple} \\ \frac{R}{1.5 p ψ_{1}} T_{e 1} (θ, ω) + \frac{L_{q}}{1.5 p ψ_{1}} \times \\ \frac{d}{dt} T_{e 1} (θ, ω) = - p ψ_{1} ω \end{matrix} \end{matrix}$ （9）

式中:T_e0为与系统运动学参数无耦合的电磁转矩项; T_e1(θ , ω )为与系统运动学参数耦合的电磁转矩项。

由于耦合转矩项T_e1(θ , ω )与转子转速、转角等运动学参数有关, 因此原振动系统的刚度、阻尼等特征都将发生改变, 进而影响电动轮系统模态特征及固有特性。

令式(9)中T_e0=0, 结合式(5)中其余运动学方程对振动系统进行复模态分析, 得到电动轮机电耦合系统模态参数如表3所示。从表3可以看出:①电动轮第3、4、5阶模态对系统振动贡献较大, 因此后面主要分析这3阶模态参数的变化规律; ②第3阶模态参数相对4、5阶参数变化较大, 而且对振动的影响也更为显著; ③模态阻尼比的改变对振动影响更为明显, 即机电耦合主要通过改变系统阻尼影响电动轮振动特性。

表3 电动轮耦合系统模态参数 Table 3 Modal parameters of electric wheel coupling model

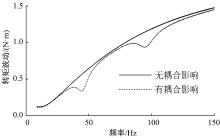
考虑电磁影响后, 电动轮模态频率和阻尼比都有所增加, 为进一步分析模态参数变化对振动特性的影响, 以T_e0为输入确定轮胎和轮辋/电机纵向振动传递函数, 并与原电动轮系统进行对比, 结果分别如图12和图13所示。

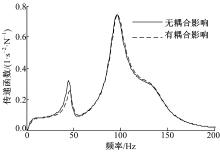	Figure Option View Download New Window
	图12 转矩波动到轮胎纵向振动加速度传递曲线对比Fig.12 Contrast of transfer function from torque ripple to tire horizontal vibration acceleration

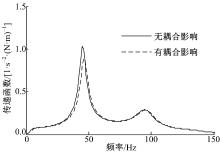	Figure Option View Download New Window
	图13 转矩波动到轮辋纵向振动加速度传递曲线对比Fig.13 Contrast of transfer function from torque ripple to rim horizontal vibration acceleration

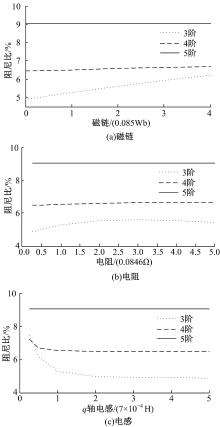
式(9)中耦合转矩项T_e1(θ , ω )同时还取决于磁链、电阻和电感等电磁参数, 因此电动轮系统模态参数还受到电磁参数的影响。图14为3~5阶模态阻尼比随电磁参数的变化规律, 可以看出:①电动轮机电耦合不影响系统第5阶模态阻尼比, 但对同向旋转模态(第3阶)阻尼比影响最大; ②在磁链、电阻和电感三者中, 磁链对模态阻尼比的影响最大, 模态阻尼比随磁链增加而线性增加; 电感对模态阻尼比的影响次之, 模态阻尼比随电感增加而降低, 最后趋于稳定; ③电阻对模态阻尼比的影响最弱, 模态阻尼比随电阻增加先缓慢增加后略有下降。

	Figure Option View Download New Window
	图14 电动轮耦合系统模态阻尼比随电磁参数变化Fig.14 Variation of modal damping ratios with electromagnetic parameters

4 结论

(1)当转矩波动引起电动轮系统共振时, 电机转子呈现出显著的转速波动, 会对轮毂电机转矩波动产生较大影响。而且由于转速波动对转矩波动影响主要表现为负反馈(削弱)作用, 在电动轮模态频率对应的电机转速下, 机电耦合的影响会使转矩波动幅值有所下降。

(2)与原电动轮系统相比, 电磁参数主要会增加电动轮耦合系统第3阶模态阻尼比, 从而降低电动轮系统在同向旋转模态频率处的共振峰值, 尤其对轮辋/电机纵向振动有明显抑制作用。

(3)磁链对电动轮耦合系统模态阻尼比的影响最大, 模态阻尼比随磁链增加而线性增加, 随电感增加而降低, 最后趋于稳定, 随电阻增加先缓慢增加而后略有下降。合理选取轮毂电机电磁参数对抑制电动轮系统振动有一定的意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Huang Xiao-yu, Wang Jun-min. Model predictive regenerative braking control for lightweight electric vehicles with in wheel motors[J]. Proceedings of the Institution of Mechanical Engineerings Part D: Journal of Automobile Engineering, 2012, 226(9): 1220-1232. [本文引用:1]
[2]	Chen Yan, Wang Jun-min. Design and evaluation on electric differentials for overactuated electric ground vehicles with four independent in-wheel motors[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1535-1542. [本文引用:1]
[3]	Wang Rong-rong, Chen Yan, Feng Dai-wei, et al. Development and performance characterization of an electric ground vehicle with independently-actuated in-wheel motors[J]. Journal of Power Sources, 2011, 196(8): 3962-3971. [本文引用:1]
[4]	Song Zi-you, Li Jian-qiu, Wei Yin-tao, et al. Interaction of in-wheel permanent magnet synchronous motor with tire dynamics[J]. Chinese Journal of Mechanical Engineering, 2015, 28(3): 470-478. [本文引用:2]
[5]	Li Jian-qiu, Song Zi-you, Wei Yin-tao, et al. Influence of tire dynamics on slip ratio estimation of independent driving wheel system[J]. Chinese Journal of Mechanical Engineering, 2014, 27(6): 1203-1210. [本文引用:2]
[6]	左曙光, 段向雷, 吴旭东. 电动轮-悬架系统台架振动特性试验分析[J]. 振动与冲击, 2014, 33(12): 165-187. Zuo Shu-guang, Duan Xiang-lei, Wu Xu-dong. Vibration test analysis of a electric wheel-suspension system on a test bed[J]. Journal of Vibration and Shock, 2014, 33(12): 165-187. [本文引用:1]
[7]	陈贵清, 杨翊仁, 邱家俊. 水电机组转子轴系扭振零频的计算和共振分析[J]. 西南交通大学学报, 2002, 37(1): 44-48. Chen Gui-qing, Yang Yi-ren, Qiu Jia-jun. Hydrogenetator rotors: zeros frequency of torsional vibration and resonance[J]. Journal of Southwest Jiaotong University, 2002, 37(1): 44-48. [本文引用:1]
[8]	徐进友, 刘建平, 宋轶民, 等. 考虑电磁激励的水轮发电机组扭转振动分析[J]. 天津大学学报, 2008, 41(12): 1411-1416. Xu Jin-you, Liu Jian-ping, Song Yi-min, et al. Torsional vibration analysis of hydrogenerators considering electromagnetic excitation[J]. Journal of Tianjin University, 2008, 41(12): 1411-1416. [本文引用:1]
[9]	Liu Shuang, Zhao Shuang-shuang, Sun Bao-ping, et al. Bifurcation and chaos analysis of a nonlinear electromechanical coupling relative rotation system[J]. Chinese Physics B, 2014, 23(9): 094501. [本文引用:1]
[10]	Chen Xing, Hu Ji-bin, Peng Zeng-xiong, et al. Nonlinear torsional vibration characteristics of PMSM for HEV considering electromagnetic excitation[J]. International Journal of Applied Electromagnetics and Mechanics, 2015, 49(1): 9-21. [本文引用:1]
[11]	Zhu Z Q, Howe D, Botle E, et al. Instantaneous magnetic field distribution in brushless permanent DC motors, Part Ι: open-circuit field[J]. IEEE Transactions on Magnetics, 1993, 29(1): 124-135. [本文引用:1]
[12]	李景灿, 廖勇. 考虑饱和及转子磁场谐波的永磁同步电机模型[J]. 中国电机工程学报, 2011, 31(3): 60-66. Li Jing-can, Liao Yong. Model of permanent magnet synchronous motor considering saturation and rotor flux harmonics[J]. Proceedings of the CSEE, 2011, 31(3): 60-66. [本文引用:1]
[13]	陈益广, 潘玉玲, 贺鑫. 永磁同步电机分数槽集中绕组磁动势[J]. 电工技术学报, 2010, 25(10): 30-36. Chen Yi-guang, Pan Yu-ling, He Xin. Magnetomotive force in permanent magnet synchronous machine with concentrated fractional-slot winding[J]. Transactions of China Electrotechnical Society, 2010, 25(10): 30-36. [本文引用:1]
[14]	Bianchi N, Bolognani S, Grezzani G. Design considerations for fractional-slot winding configurations of synchronous machines[J]. IEEE Transactions on Industrial Application, 2006, 42(4): 997-1006. [本文引用:1]
[15]	左曙光, 段向雷, 吴旭东. 电动轮刚性环耦合特性模型建模与分析[J]. 同济大学学报: 自然科学版, 2014, 42(10): 1578-1585. Zuo Shu-guang, Duan Xiang-lei, Wu Xu-dong. Modeling and analysis of rigid ring coupling model of electric wheel[J]. Journal of Tongji University(Natural Science), 2014, 42(10): 1578-1585. [本文引用:2]
[16]	董恒, 王辉, 黄科元. 永磁同步电动机驱动系统数字PI调节器参数设计[J]. 电气传动, 2009, 39(1): 7-10. Dong Heng, Wang Hui, Huang Ke-yuan. Design of PMSM drive system digital PI adjuster parameters[J]. Electric Drive, 2009, 39(1): 7-10. [本文引用:1]

2012

0.0

... 0 引言轮毂电机驱动电动汽车以其在车辆总体结构布置、底盘主动控制以及操纵性等方面的明显优势成为未来电动汽车的发展方向,其关键部件之一的电动轮系统也因此成为开发研究的核心^[1,2,3] ...

2012

0.0

2011

0.0

2015

0.0

... 清华大学Song^[4]和Li^[5]等分析了轮毂电机驱动下轮胎的扭转振动、滑移率及纵向力波动等现象,并指出上述动力学行为由轮毂电机电磁转矩和轮胎弹性结构耦合作用引起 ...

... 对于轮毂电机驱动控制系统,一般不存在速度和位移闭环^[4,5],因此本文采用d/q轴电流单闭环控制系统进行简化 ...

2014

0.0

... 对于轮毂电机驱动控制系统,一般不存在速度和位移闭环^[4,5],因此本文采用d/q轴电流单闭环控制系统进行简化 ...

2014

0.0

... 左曙光等^[6]进一步通过电动轮台架试验发现了轮毂电机转矩波动引起的电动轮-悬架系统的阶次振动,并分析了电机转速和负载转矩等参数对振动的影响 ...

2002

0.0

... 在电机系统的机电耦合影响机理研究方面,陈贵清^[7]和徐进友^[8]等分析了电磁激励作用下水轮发电机组转子轴系的机电耦合扭转振动特性,指出由于受到电磁约束作用,振动系统会出现零阶固有频率,受时变电磁刚度的影响,系统稳态响应对电磁参数变化敏感 ...

2008

0.0

2014

0.0

... Liu^[9]和Chen^[10]等先后针对异步电机和永磁同步电机驱动机电耦合系统的分叉和混沌等非线性特征进行了研究,但同样基于开环仿真无法反映定子电流的影响,而且文中基于简单的两自由度扭振模型未能真实反映电动机驱动系统动力学特征,尤其不适用于电动轮振动复杂的系统 ...

2015

0.0

1993

0.0

... 1 考虑永磁体磁场谐波的电机数学模型永磁同步电机理想模型假设永磁体磁场在气隙中呈现正弦分布,但实际上由于永磁体磁极受制造及工艺上的限制,气隙中永磁体磁场在空间并不呈理想正弦分布而是存在一定的谐波^[11],进而使永磁体在三相绕组中感应的磁链存在谐波,可表示为: ...

2011

0.0

... 结合磁链表达式,并由定子绕组电压平衡关系和转矩方程可以确定考虑永磁体磁场谐波时d/q轴坐标系下电机数学模型为^[12]: ...

2010

0.0

2006

0.0

2014

0.0

... 2 电动轮系统动力学建模及固有特性分析由前期研究可知^[15],轮毂电机转矩波动主要引起电动轮系统扭转和纵向振动,因此,本文考虑轮胎弹性动力学特征,建立包括轮胎和轮辋/电机等质量的扭转和纵向平移自由度的振动模型:轮胎和轮辋/电机通过胎侧连接,将其等效为扭转刚度和纵向平移刚度 ...

... 该模型对于反映轮毂电机转矩波动下电动轮振动特性的适用性已通过台架试验得到验证^[15] ...

2009

0.0