基于汽缸压力辨识的发动机失火故障诊断

引用本文

王德军, 吕志超, 王启明, 张贤达, 王子健. 基于汽缸压力辨识的发动机失火故障诊断. 吉林大学学报(工学版), 2017, 47(3): 917-923
WANG De-jun, LYU Zhi-chao, WANG Qi-ming, ZHANG Xian-da, WANG Zi-jian. Engine misfire fault diagnosis based on cylinder pressure identification. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 917-923 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703031
Permissions

基于汽缸压力辨识的发动机失火故障诊断

王德军¹, 吕志超¹, 王启明², 张贤达¹, 王子健¹

1.吉林大学通信工程学院,长春130022

2.吉林大学交通学院,长春130022

作者简介:王德军(1970-),男,副教授,博士.研究方向:复杂系统故障诊断及容错控制.E-mail:djwang@jlu.edu.cn

基金项目:国家自然科学基金国际(地区)合作与交流重点项目(61520106008)

摘要

针对发动机失火故障,提出了一种利用傅里叶级数和L-M算法优化BP神经网络的故障诊断方法。利用AMESim发动机模型进行稳态工况实时仿真,应用L-M算法优化BP神经网络预测节气门开度与发动机汽缸做功频率的关系,同时借助傅里叶级数辨识缸内压力,将由曲轴转速实时映射的汽缸压力模型与所辨识的缸内压力模型进行比较,得出失火诊断结果;并对辨识的压力模型进行相位和频率补偿,提高了诊断精度及诊断方法泛化性。在出现失火故障后再次进行相位和频率补偿,使辨识的模型具有强跟踪性。任取两个节气门开度值进行试验验证,结果表明:本文方法在发动机稳态工况下,无论高转速小负载还是低转速大负载,均可以准确识别出单缸连续失火故障和多缸随机失火故障,验证了本文方法的准确性。

关键词: 自动控制技术; 傅里叶级数; BP神经网络; 发动机失火故障; 发动机汽缸压力; AMESim

中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2017)03-0917-07

Engine misfire fault diagnosis based on cylinder pressure identification

WANG De-jun¹, LYU Zhi-chao¹, WANG Qi-ming², ZHANG Xian-da¹, WANG Zi-jian¹

1.College of Communication Engineering, Jilin Universityi,Changchun 130022,China

2.College of Transportation, Jilin University, Changchun 130022,China

Abstract

In order to solve the problem of engine misfire fault, a diagnosis method based on cylinder pressure identified by Fourier Transform (FT) and L-M optimized BP neural network is proposed. The BP neural network is trained by the steady state simulation data from AMESim to obtain the relationship between open value of valve and frequency, and FT is used to identify the cylinder pressure. The misfire failure can be diagnosed by comparison of the FT identified pressure with the pressure mapped from crank speed. By offsetting the phase and frequency of the identified model, the accuracy and generalization of the identified model are improved. When misfire fault occurs, high tracking ability can be obtained by re-offsetting the phase and frequency of the identified model. Two random and independent open values of the valve are used to verify the proposed method, Results show that no matter engine at high speed with light load condition or at low speed with heavy load condition, this method can precisely diagnose the signal-cylinder continuous misfire fault and multi-cylinder random misfire fault.

Key words: automatic control technology; Fourier series; BP neural network; engine misfire fault; engine cylinder pressure; AMESim

Show Figures

0 引言

现阶段国内、外针对发动机失火故障诊断的策略主要围绕曲轴输出端信号进行, 由于此信号是可以直接测量的, 且通过对信号的处理, 可以得到相应的故障诊断信息。文献[1]利用参数化的卡尔曼滤波器设计转矩观测算法, 通过为每个汽缸都配置两个卡尔曼滤波器, 其中一个用来预测正常状态, 另一个用来预测失火的方式确保失火诊断系统的可靠性。文献[2]将汽缸做功产生的能量作为系统输入、曲轴转速作为系统输出, 首先在工作点附近把做功过程线性化, 然后基于线性化的过程建模, 由于对系统线性化过程本身就存在误差, 而且此误差是无法预测和处理的, 因此故障算法存在一定误差。文献[3]对飞轮由于制造精度问题引起的对既成算法泛化性的负面影响进行了算法补偿, 以减小由于“ 车-车” 间的物理误差引起的既成算法精度的下降。此外, 傅里叶变换、小波分析^[4]、傅里叶变换与神经网络融合算法^[5]等由于他们各自的特性也逐渐被重视。虽然基于曲轴端输出信号的诊断方法应用较广, 但对高转速低负荷工况下的失火故障及多缸失火故障诊断时仍然存在不足^[6]。当出现外在干扰或负载变化, 且干扰或负载频率特性或某些其他特征值接近于失火状态的频率特性或某些其他特征值时, 曲轴输出端将会出现输出信号的叠加和混叠, 导致基于曲轴输出信号的诊断方法无法准确识别和分辨出失火故障信号和干扰信号, 致使基于曲轴输出端信号的方法的效率下降甚至失效。制造业的机械加工存在物理误差, 测量发动机输出端数据又存在测量误差和发动机内部多项噪声的耦合, 所以为了减少误差源, 提高精度, 直接从发动机内部提取能表示发动机内部燃烧状态的特征量变得十分重要。文献[7]通过测量半转周期, 并求得发动机的粗暴度, 然后利用粗暴度的大小设置报警阈值。但是经反复试验发现该失火诊断算法偶尔会出现不能准确诊断多缸随机失火的情况, 容易误判失火发生的汽缸^[8]。发动机失火故障发生后, 最直接的表现即为发动机缸压值的剧烈变化, 发动机内部燃烧推动了曲轴的运转, 决定了曲轴转速的变化量, 而汽缸压力是发动机内部燃烧的重要表现形式, 所以基于发动机压力的诊断方法是最准确的。但侵入式发动机压力传感器由于造价高, 运行环境过于恶劣导致寿命短、精度低等问题, 所以, 利用辨识拟合的无侵入式的缸压实时监控系统变得越来越重要。发动机汽缸由于其做功的方式决定了不同节气门开度会对应不同的做功频率, 且二者呈现非线性变化关系; 同时, 也决定了缸内压力变化和输出转矩乃至曲轴转速必定是周期信号, 不同工况下的缸内压力信号虽然会有不同的频率和幅值, 但是波形却都是大体一致的。对于非线性系统的预测采用训练神经网络的方式; 而对于周期信号的分析, 傅里叶变换有其独特的优势^[9]。

综上, 本文提出了基于观测气缸压力的失火故障诊断方法。应用L-M算法优化BP神经网络预测节气门开度与发动机气缸做功频率的关系, 同时借助傅里叶级数辨识缸内压力, 得出失火诊断结果。再通过误差补偿的方式提高本文方法的精确性。本文方法深入发动机的内部, 从其内部机理的角度对发动机做功过程进行监控。相较于利用曲轴输出端信号为基础的诊断方法, 本文方法抗干扰性更强。在稳态工况下, 无论在高转速还是低转速, 大负载还是小负载条件下都能准确识别出单缸连续失火还是多缸随机失火故障。

1 失火故障诊断原理

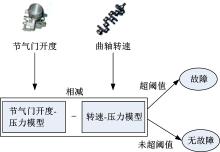
当发动机在稳态工况中发生失火故障时, 缸内的实际压力通过曲轴转速表现出非常大的衰减, 与无失火故障时的缸压有比较大的差值变化, 而且汽缸失火引起其他缸的振动会进一步强化这个差值。首先辨识无故障时的节气门开度-压力模型; 然后用此模型与曲轴转速映射出的转速-压力模型进行比较, 得出该差值并进行故障诊断, 原理如图1所示。

	Figure Option View Download New Window
	图1 故障诊断原理图Fig.1 Schematic diagram of fault diagnosis method

1.1 汽缸压力数学模型

发动机汽缸的做功过程就是通过燃烧将燃料的化学能转化为机械能的热力学过程, 发动机汽缸压力的数学模型可近似等效如下:

$\frac{dp}{dt} = ρ (\frac{dr}{dt} T + r \frac{dT}{dt}) + \frac{dρ}{dt} rT$ (1)

$T = \frac{p}{ρr}$ (2)

$\begin{matrix} r = \sum_{i} x_{i} r_{i} \end{matrix}$ (3)

式中:p为缸内气压; T为汽缸内部的温度; r为理想气体常数; x_i为i时刻汽缸中燃油、空气和尾气混合物的体积分数; r_i为对应于x_i的理想气体常数; ρ 为气体密度; t为时间。

1.2 L-M算法优化的BP神经网络模型

通过分析发动机汽缸的数学模型和做功过程可知:在稳态工况下, 发动机节气门的开度直接影响发动机的做功频率。二者虽然变化趋势相同, 但其变化关系却是非线性, 因此本文借助神经网络对非线性系统强大的逼近识别预测能力对数据进行处理。但是神经网络需要大信息量样本数据进行训练, 而且一旦训练样本范围外的数据的变化规律与训练样本的变化规律不一致, 预测的精度将会大打折扣^[10]。本文提出用神经网络辨识节气门开度与发动机做功频率的关系, 然后对预测的数据进行相位和频率的补偿, 使得补偿后的神经网络预测数据拥有更高的精度。

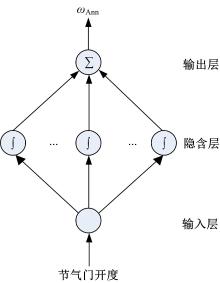
	Figure Option View Download New Window
	图2 三层人工神经网络示意图Fig.2 Schematic of 3-layer artificial neural network

本文利用人工神经网络预测节气门开度-发动机做功频率, 属于单输入、单输出的非线性系统, 三层的BP神经网络可以实现任意的n维到m维的映射。因此可选择三层人工神经网络, 包括输入层、输出层和隐含层, 如图2所示。其中, 基于数据的分布规则采用试凑法与经验公式相结合的方法确定隐含层节点数目为3^[11]。由于tansig函数作为隐含层激励函数时能够快速、有效地收敛, 满足计算要求; purelin线性函数能够对误差做出快速响应, 加快训练速度。因此, 本文选择tansig函数作为隐含层激励函数; purelin函数作为输出层激励函数。借助神经网络在非线性系统预测上的独特优势, 从而预测本文中的节气门开度与汽缸做功周期的非线性关系。

1.3 傅里叶级数数学模型

发动机汽缸由于其旋转做功的方式决定了输出是波形大体一致的周期信号。而对于周期信号的辨识, 傅里叶级数有其独特优势, 它能将满足一定条件的某个函数表示成三角函数的线性组合。根据傅里叶变换的相关理论, 任何连续测量的信号都可以表示为不同频率的正弦波信号的无限叠加。如果一个信号f(x)是周期的, 那么对于一切x, 存在某个正值L, 有f(x)=f(x+L), 基波周期就是满足上式的最小非零正值L, 而ω ₀=2π /L称为基波频率, 因此傅里叶级数的计算公式为:

$\begin{matrix} f (x) = a_{0} + \overset{\infty}{\sum_{n = 1}} (a_{n} cosnx \frac{2 π}{L} + b_{n} sinnx \frac{2 π}{L}) \end{matrix}$ (4)

式中:a₀为信号的截距; a_n、b_n为各阶傅里叶级数的系数^[12]。

2 失火故障诊断方法

2.1 转速-汽缸压力模型

在稳态工况下, 转速-压力的模型如下^[13]:

$\begin{matrix} ω' = \frac{1}{J (θ)} [- \frac{1}{2} \frac{dJ (θ)}{dθ} ω^{2} + T_{i} + T_{l} + T_{f}] \end{matrix}$ (5)

式中:ω 为曲轴角速度; θ 为曲柄转角; T_i为指示转矩; T_f为摩擦转矩; T_l为负荷转矩; J $\begin{matrix} (θ) \end{matrix}$ 为发动机曲轴等效集中转动惯量, 是曲柄转角的函数。

$\begin{matrix} T_{i} = \overset{n}{\sum_{j = 1}} p_{j} A_{j} L_{tor, j} \end{matrix}$ (6)

式中:p_j为第j缸内气体压力; A_j为第j缸活塞顶面积; L_tor,_j为汽缸压力的有效力矩, 由曲柄半径R、曲柄长度L、活塞中心偏移量E决定。

在AMESim运行环境中, 4个汽缸视为等价, 取j=1, n=4。发动机稳态输出时, 转矩输出主要是指示转矩 $\begin{matrix} {T_{i}}^{[14]} \end{matrix}$ , 其他部分转矩可近似视为常数F, 于是将式(6)代入式(5)可得:

$\begin{matrix} p_{1} = \frac{J (θ) ω'}{4 A_{1} L_{tor, 1}} + F \end{matrix}$ (7)

通过式(7)可知, 在故障诊断方面, 曲轴转速的导数与发动机汽缸内部压力存在实时映射关系。通过对转速数据求微分、归一化等方法可以建立相应模型并消除系数的影响。

2.2 节气门开度-汽缸压力模型

节气门开度-汽缸压力辨识模型的流程为:首先利用神经网络预测汽缸做功频率; 然后对该频率进行补偿。以补偿后的频率为基频对缸压信号进行傅里叶级数辨识。当出现失火故障后, 汽缸做功频率和相位会发生变化, 针对变化需再次进行补偿。

2.2.1 汽缸做功频率模型

利用傅里叶级数对节气门开度-汽缸压力模型进行辨识时, 需先确定傅里叶级数的基频ω _f。本文利用AMESim进行大量的数据仿真, 基于神经网络对节气门开度-做功频率模型进行非线性预测, 得到不同节气门开度下的做功预测频率ω _Ann, 通过计算转速信号在做功预测周期1/ω _Ann内的信号峰值与信号谷值的时间差T_fre1进行频率补偿, 从而精准地实时反映发动机汽缸的做功周期状态。频率补偿后的基频计算公式为:

$\begin{matrix} ω_{f} = π / T_{fre 1} \end{matrix}$ (8)

2.2.2 汽缸压力模型

考虑到不同工况下的缸内压力信号有不同的频率和幅值, 但是波形都是大体一致的特点, 利用AMESim进行发动机在稳态工况下的做功过程的仿真, 然后利用AMESim仿真数据辨识发动机汽缸的压力, 并做归一化处理, 与转速-缸压模型保持一致, 使其能够反映稳态工况下其他任意环境下的汽缸压力。考虑到工程实际和成本问题, 结合缸内压力的辨识过程, 可选四阶傅里叶级数进行辨识, 其数学模型为:

$\begin{matrix} \begin{matrix} f (x) = a_{0} + a_{1} \cos ω_{f} x + b_{1} \sin ω_{f} x + \\ a_{2} \cos 2 ω_{f} x + b_{2} \sin 2 ω_{f} x + \\ a_{3} \cos 3 ω_{f} x + b_{3} \sin 3 ω_{f} x + \\ a_{4} \cos 4 ω_{f} x + b_{4} \sin 4 ω_{f} x \end{matrix} \end{matrix}$ （9）

式中:x为时间, ms。

得到做功频率和压力数学模型后, 通过计算本文模型压力信号与转速-压力模型信号在同周期内的峰值时间差T_pha1进行相位补偿, 相位补偿计算公式如下:

$\begin{matrix} x_{f} = x + T_{pha 1} \end{matrix}$ （10）

因此, 发动机汽缸压力的辨识模型为:

$\begin{matrix} \begin{matrix} f (x) = a_{0} + \\ a_{1} \cos ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) + \\ b_{1} \sin ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) + \\ a_{2} \cos 2 ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) + \\ b_{2} \sin 2 ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) + \\ a_{3} \cos 3 ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) + \\ b_{3} \sin 3 ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) + \\ a_{4} \cos 4 ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) + \\ b_{4} \sin 4 ((\frac{π}{T_{fre 1}}) (x + T_{pha 1})) \end{matrix} \end{matrix}$ （11）

2.2.3 失火故障后的模型自补偿

当发生失火故障时, 发动机的做功频率改变, 同时引起相位差, 此时需再次对模型进行频率和相位补偿, 可用Simulink中的Enable模块实现。补偿机制功能为在原信号基础上, 再次通过计算转速信号在做功周期内的信号峰值与信号谷值的时间差T_fre2进行频率补偿, 再次通过计算本文模型压力信号与转速-压力模型信号在同周期内的峰值时间差T_pha2进行相位补偿, 发生多少次失火故障, 就要进行多少次补偿。补偿后的节气门开度-压力模型为:

$f (x) = a_{0} + a_{1} \cos [ω (x + φ)] + b_{1} \sin [ω (x + φ)] + a_{2} \cos 2 [ω (x + φ)] +$

$b_{2} \sin 2 [ω (x + φ)] + a_{3} \cos 3 [ω (x + φ)] + b_{3} \sin 3 [ω (x + φ)] +$

$a s 4 [ω (x + φ)] + b_{4} \sin 4 [ω (x + φ)]$ (12)

$ω = π / T_{freN}$ (13)

$\begin{matrix} φ = T_{pha 1} + T_{pha 2} + \dots + T_{phaN} \end{matrix}$ (14)

式中:N为失火次数。

3 仿真验证及结果分析

针对通用的失火故障诊断方法中存在的随机失火诊断出现误差和处于高转速低负荷或低转速高负荷情况下出现的误判, 本文在设计仿真工况时加恒定负载, 取节气门开度为27° (转速为4000 r/min)、20° (转速为2800 r/min)和15° (转速为1200 r/min), 模拟高转速低负荷、中转速和低转速高负荷的工况。并对3个汽缸进行随机故障输入, 模拟多缸随机失火和单缸连续失火工况。

3.1 仿真环境设置

AMESim是基于直观的图形界面的仿真平台, 在整个仿真过程中系统模型可以显示在该平台中。本文采用AMESim Demo中自带的四缸四冲程自然吸气发动机模块, 参数按照默认值设置, 如表1所示。

表1 AMESim模块参数 Table 1 Parameters of AMESim model

在此AMESim模型参数设置下, 可得到辨识模型的参数, 如表2所示。

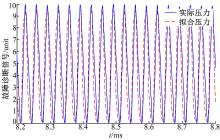
将本文辨识的发动机内部压力模型与AMESim中的仿真数据进行对比, 如图3所示。

从图3可以看出, 辨识的发动机内部压力很好地跟踪了AMESim中的仿真数据。

在Simulink中搭建本故障诊断系统的仿真模型, 如图4所示。

表2 模型参数 Table 2 Parameters of identification model

	Figure Option View Download New Window
	图3 AMESim仿真数据与辨识模型数据对比Fig.3 Comparison between AMESim simulation and identification model

	Figure Option View Download New Window
	图4 发动机失火故障诊断系统的Simulink实现Fig.4 System realization by Simulink

3.2 结果分析

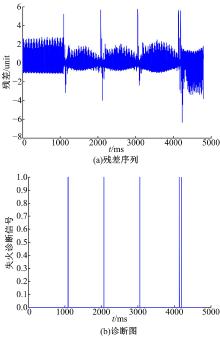
利用AMESim模拟延后点火提前角至-40° 时的失火故障。节气门开度为20° 时, 采用AMESim的仿真数据对本文故障诊断系统进行测试, 仿真时间为4.8 s; 采样时间为0.001 s; 随机在1.09、2.07、3.05 s注入多缸随机失火故障, 在4.13 s注入单缸连续2次失火故障。残差序列如图5(a)所示, 当失火故障发生时, 残差序列在对应时刻出现了明显变化, 基于此取阈值为3.5 unit, 当残差输出大于3.5 unit时认定为失火故障。通过对残差序列的处理可将大于等于阈值的数据以逻辑“ 1” 的形式输出, 小于阈值的数据以逻辑“ 0” 的形式输出, 由图5(b)知, 系统精确地诊断出了失火故障。此时系统输出为“ 1” 时代表汽缸有失火故障发生。

	Figure Option View Download New Window
	图5 仿真结果(节气门开度取20° )Fig.5 Simulation results when throttle valve at 20°

针对高转速小负载和低转速大负载情况的故障诊断, 分别选择节气门开度为15° 和27° 工况进行验证。

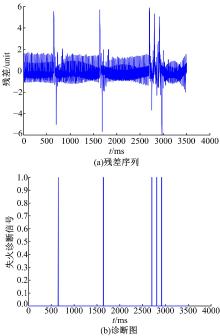
当节气门开度为15° 时, 将延后点火提前角至-40° , 模拟失火故障, 并加恒定大负载。用AMESim的仿真数据对本故障诊断系统进行测试, 仿真时间为3.5 s; 采样时间为0.001 s; 随机在0.65、1.63 s注入多缸随机失火故障, 在2.70 s注入单缸连续3次失火故障。残差序列如图6(a)所示, 诊断结果如图6(b)所示。

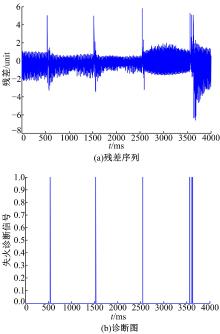
	Figure Option View Download New Window
	图6 仿真结果(节气门开度取15° )Fig.6 Simulation results when throttle valve at 15°

当节气门开度为27° 时, 将延后点火提前角至-40° , 模拟失火故障, 并加恒定小负载。用AMESim的仿真数据对本文故障诊断系统进行测试, 仿真时间为4 s; 采样时间为0.001 s; 随机在0.53、1.52、2.54 s注入多缸随机失火故障, 在3.56 s注入单缸连续3次失火故障。残差序列如图7(a)所示, 诊断结果如图7(b)所示。

	Figure Option View Download New Window
	图7 仿真结果(节气门开度取27° )Fig.7 Simulation results when throttle valve at 27°

由仿真及检测结果知, 模型对失火故障的诊断是精确的。且无论在高转速小负载还是低转速大负载工况下, 当出现多缸随机失火和单缸连续失火时, 残差序列的输出值在故障时刻均有非常大的跳变, 根据此跳变合理地设计阈值, 系统便可以精确地给出报警信息, 此时, 结合曲轴转角传感器读出失火故障发生时每个汽缸活塞所在的位置, 即可对失火的汽缸进行定位。

4 结束语

提出了一种以辨识发动机汽缸内部压力为核心, 以曲轴转速与发动机缸压的实时对应关系为诊断手段的发动机失火故障诊断方法。相较之前通用的失火故障检方法中存在的随机失火诊断出现的误差和当处于高转速低负荷或低转速高负荷情况下的误判, 本文方法利用AMESim模拟高转速低负荷和低转速高负荷工况, 并在任意节气门开度下注入随机失火故障进行仿真验证, 结果证明了本文方法对单缸连续失火和多缸随机失火故障诊断的有效性、高精度性和强抗干扰性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Helm S, Kozek M, Jakubek S. Combustion torque estimation and misfirre detection for calibration of combustion engines by parametric Kalman filtering[J]. IEEE Transactions on Industrial Electronics, 2012, 59(11): 4326-4337. [本文引用:1]
[2]	Rizvi M A, Bhatti A I, Butt Q R. Hybrid model of the gasoline engine for misfire detection[J]. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3680-3692. [本文引用:1]
[3]	Jung D, Frisk E, Krysand er M. A flywheel error compensation algorithm for engine misfire detection[J]. Control Engineering Practice, 2016, 47: 37-47. [本文引用:1]
[4]	杨梅, 张振文, 孙宏强, 等. 小波分析与傅里叶分析的比较及其在故障诊断中的应用[J]. 中国测试技术, 2005, 31(2): 58-60. Yang Mei, Zhang Zhen-wen, Sun Hong-qiang, et al. The comparison of wavelet and Fourier analysis and their application to fault diagnosis[J]. China Measurement Technology, 2005, 31(2): 58-60. [本文引用:1]
[5]	Wu Z J, Lee A. Misfire detection using a dynamic neural network with output feedback[J]. SAE Paper, 980515. [本文引用:1]
[6]	胡重庆, 李艾华, 朱春红, 等. 基于瞬时转速统计分析的内燃机失火检测[J]. 内燃机学报, 2009, 27(5): 446-451. Hu Chong-qing, Li Ai-hua, Zhu Chun-hong, et al. Misfire detection based on statistical analysis of instantaneous rational speed[J]. Transactions of CSICE, 2009, 27(5): 446-451. [本文引用:1]
[7]	Wang Yin-hui, Huang Kai-sheng, Lin Zhi-hua, et al. Advanced gasoline engine misfire diagnostic method based on crankshaft speed multiple filtering[DB/OL]. [2016-03-27]. http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=5776855. [本文引用:1]
[8]	王银辉, 黄开胜, 林志华, 等. 发动机多缸随机失火诊断算法研究[J]. 内燃机工程, 2012, 33(1): 18-26. Wang Yin-hui, Huang Kai-sheng, Lin Zhi-hua, et al. Study of engine multi-cylinder rand om misfire detection[J]. Chinese Internal Combustion Engine Engineering, 2012, 33(1): 18-26. [本文引用:1]
[9]	褚金奎, 孙建伟. 基于傅里叶级数理论的连杆机构轨迹综合方法[J]. 机械工程学报, 2010, 46(13): 31-41. Chu Jin-kui, Sun Jian-wei. Unified approach to synthesis of coupler curves of linkage by Fourier series[J]. Journal of Mechanical Engineering, 2010, 46(13): 31-41. [本文引用:1]
[10]	胡杰, 颜伏伍. 基于BP神经网络的汽油机失火故障诊断方法的研究[J]. 汽车工程, 2011, 33(2): 101-105. Hu Jie, Yan Fu-wu. A research on the misfire diagnosis method of gasoline engine based on BP neural network[J]. Automotive Engineering, 2011, 33(2): 101-105. [本文引用:1]
[11]	沈花玉, 王兆霞, 高成耀, 等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报, 2008, 24(5): 13-15. Shen Hua-yu, Wang Zhao-xia, Gao Cheng-yao, et al. Determining the number of BP neural network hidden layer units[J]. Journal of Tianjin University of Technology, 2008, 24(5): 13-15. [本文引用:1]
[12]	奥本海默. 信号与系统[M]. 刘树棠译. 2版. 西安: 西安交通大学出版社, 2005. [本文引用:1]
[13]	王赟松, 褚福磊, 郭丹. 基于二阶滑模技术的内燃机气缸压力的估计[J]. 内燃机学报, 2004, 22(6): 555-561. Wang Yun-song, Chu Fu-lei, Guo Dan. Cylinder pressure estimation for engines using second-order sliding modes[J]. Transactions of CSICE, 2004, 22(6): 555-561. [本文引用:1]
[14]	于明进, 程勇, 吴波, 等. 试验确定发动机转动惯量的一种新方法[J]. 农业机械学报, 2005, 36(7): 34-37. Yu Ming-jin, Cheng Yong, Wu Bo, et al. New method for estimating the inertia moment of an engine[J]. Transactions of the Chinese Society for Agricultural Machinery, 2005, 36(7): 34-37. [本文引用:1]

2012

0.0

2011

0.0

2016

0.0

2005

0.0

. 2005, 31(2):58-60

The comparison of wavelet and Fourier analysis and their application to fault diagnosis

小波分析与傅里叶分析的比较及其在故障诊断中的应用

Yang Mei , Zhang Zhen-wen , Sun Hong-qiang

杨梅, 张振文, 孙宏强

... 此外,傅里叶变换、小波分析^[4]、傅里叶变换与神经网络融合算法^[5]等由于他们各自的特性也逐渐被重视 ...

0.0

... 此外,傅里叶变换、小波分析^[4]、傅里叶变换与神经网络融合算法^[5]等由于他们各自的特性也逐渐被重视 ...

2009

0.0

. 2009, 27(5):446-451

Misfire detection based on statistical analysis of instantaneous rational speed

基于瞬时转速统计分析的内燃机失火检测

Hu Chong-qing , Li Ai-hua , Zhu Chun-hong

胡重庆, 李艾华, 朱春红

... 虽然基于曲轴端输出信号的诊断方法应用较广,但对高转速低负荷工况下的失火故障及多缸失火故障诊断时仍然存在不足^[6] ...

0.0

2012

0.0

. 2012, 33(1):18-26 DOI:doi:10.3969/j.issn.1000-0925.2012.01.004

Study of engine multi-cylinder random misfire detection

发动机多缸随机失火诊断算法研究

Wang Yin-hui , Huang Kai-sheng , Lin Zhi-hua

王银辉, 黄开胜, 林志华

失火诊断是发动机在线故障诊断系统的重要内容,基于曲轴转速波动进行失火诊断是目前的常用方法.针对发动机多缸随机失火,在奇瑞477F汽油机上进行试验研究,提出了采用时域滑动平均方法修正的失火诊断算法.试验证明,该算法不需要进行断油自学习修正和供油自学习修正即可准确检测多缸随机失火.

... 但是经反复试验发现该失火诊断算法偶尔会出现不能准确诊断多缸随机失火的情况,容易误判失火发生的汽缸^[8] ...

2010

0.0

. 2010, 46(13):31-41 DOI:doi:10.3901/JEM.2010.13.031

Unified approach to synthesis of coupler curves of linkage by Fourier series

基于傅里叶级数理论的连杆机构轨迹综合方法

Chu Jin-kui , Sun Jian-wei.

褚金奎, 孙建伟

探讨傅里叶级数在平面和空间连杆机构中的几何意义,给出平面和空间连杆机构连杆曲线的统一数学表达式.借助傅里叶级数理论,对该表达式的谐波成分进行理论分析,发现连杆曲线谐波成分与其相应连杆转角函数谐波特征参数和机构尺寸参数的内在联系.通过连杆机构基本尺寸型与连杆转角函数的关系,提出建立连杆曲线数值图谱,以及推导连杆机构实际尺寸、连杆上点的位置和安装尺寸参数理论公式的一般方法.建立由平面机构到空间机构在形式上和内容上统一的连杆机构轨迹综合理论.从而为连杆机构轨迹综合提供了一种有效的通用方法.最后通过空间连杆机构轨迹综合算例.说明了本方法的有效性.

... 而对于周期信号的分析,傅里叶变换有其独特的优势^[9] ...

2011

0.0

. 2011, 33(2):101-105

A research on the misfire diagnosis method of gasoline engine based on BP neural network

基于BP神经网络的汽油机失火故障诊断方法的研究

Hu Jie , Yan Fu-wu.

胡杰, 颜伏伍

针对基于曲轴瞬时角加速度的一般失火故障诊断算法能诊断失火故障,但未能有效区分故障模式的缺陷,提出了一种基于做功时间和BP神经网络的失火诊断算法.根据不同模式下各缸做功时间的波动,提取诊断循环内各缸做功时间信号的特征参数,结合BP神经网络模式识别功能,实现不同模式下的失火故障诊断.通过台架试验,测试了在正常工作、第3缸单次失火、第2缸和第3缸连续失火及第3缸连续失火4种不同模式下的失火诊断情况,结果表明,这种诊断算法能够有效识别不同失火故障模式和定位失火气缸.

... 但是神经网络需要大信息量样本数据进行训练,而且一旦训练样本范围外的数据的变化规律与训练样本的变化规律不一致,预测的精度将会大打折扣^[10] ...

2008

0.0

. 2008, 24(5):13-15 DOI:doi:10.3969/j.issn.1673-095X.2008.05.004

Determining the number of BP neural network hidden layer units

BP神经网络隐含层单元数的确定

Shen Hua-yu , Wang Zhao-xia , Gao Cheng-yao

沈花玉, 王兆霞, 高成耀

本文针对BP神经网络隐含层单元数难以确定的问题,提出了一种改进的方法,并通过实验证明该方法有效的减少了验证次数,提高了确定隐含层最佳单元数的效率,具有较高的应用价值.

... 其中,基于数据的分布规则采用试凑法与经验公式相结合的方法确定隐含层节点数目为3^[11] ...

2005

0.0

... a_n、b_n为各阶傅里叶级数的系数^[12] ...

2004

0.0

. 2004, 22(6):555-561 DOI:doi:10.3321/j.issn:1000-0909.2004.06.014

Cylinder pressure estimation for engines using second-order sliding modes

基于二阶滑模技术的内燃机气缸压力的估计

Wang Yun-song , Chu Fu-lei , Guo Dan.

王赟松, 褚福磊, 郭丹

气缸压力是内燃机燃烧分析或故障诊断的重要参数.提出了一种新的内燃机气缸压力的估计方法,应用二阶滑模控制理论对测量的曲轴转速进行实时微分,在线估计指示转矩;以估计的指示转矩作注射信号,对气缸压力估计器不断进行修正,通过合理选择增益,确保气缸压力误差动力学稳定性,最终得到气缸压力估计值.仿真结果表明,基于二阶滑模方法的气缸压力估计方法是可行的,具有较高的精度;而且该算法只需要测量发动机转速信号,方法简单可靠,成本低.

... 1 转速-汽缸压力模型在稳态工况下,转速-压力的模型如下^[13]: ...

2005

0.0

. 2005, 36(7):34-37 DOI:doi:10.3969/j.issn.1000-1298.2005.06.010

New method for estimating the inertia moment of an engine

试验确定发动机转动惯量的一种新方法

Yu Ming-jin , Cheng Yong , Wu Bo

于明进, 程勇, 吴波

提出了一种确定发动机转动惯量的方法--空载加速减速法,它是在发动机空载加速和停油减速过程中,测出发动机的瞬时转速以及气缸压力,推算得出转动惯量.在185型柴油机上进行的试验结果表明,该方法误差在2%以下.根据实测结果,对影响该方法精度的因素进行了讨论,提出了改进措施.