基于模型的诊断是人工智能领域重要的研究课题之一。在求解基于模型诊断的问题时, 将候选诊断解描述为所有的极小冲突集, 而求解所有的极小碰集是一个NP-hard问题。极小碰集是基于模型诊断的核心问题, 随着对极小碰集的深入研究, 其求解被广泛应用到其他理论和实际问题中, 如基于位向量交集运算的规则冲突检测、选课问题等^[1]。这类问题都是求与已知集合簇中的集合都有交集的极小集合。对于求解不同极小碰集的问题, 有些需要求出全部极小碰集, 而有些特殊问题只需求出一些特殊极小碰集, 例如具有最小长度的极小碰集, 即最小碰集。这类特殊碰集已经在很多的实际问题中得到应用, 如最小集合覆盖^[2]、最小碰点覆盖^[3]等。

极小碰集的求解算法主要包括完备算法和不完备算法。最早的完备求解极小碰集算法是由人工智能领域专家Reiter于1987年提出的HS-Tree算法^[4]。在集合枚举树结构的基础上, HS-DAG算法^[5]加入剪枝策略并提高了求解的精度, HST-Tree算法^[6]选择性地生成子树结点, 有效地减少了时间复杂度。此外, 还有Boolean算法^[7], DMDSE-Tree算法^[8], HS-TRIX算法^[9], CHS-Tree算法^[10], CSP-MHS^[11]算法等。上述完备算法大部分是基于搜索树的算法, 这些算法通过加入一些选择和剪枝策略, 减少搜索空间, 实现加速求解, 但是随问题规模的不断变大, 这些算法的运行时间呈现指数级增加, 且因为储存节点过多也存在空间爆炸的问题。

针对完备算法的效率和空间问题, 不完备求解极小碰集的算法陆续被提出, 虽然这些算法能够有效地求出部分或者一些特殊性质的极小碰集, 但不能保证求出所有极小碰集。Lin等^[12]提出基于遗传算法的求解极小碰集算法。张楠等^[13]提出基于粒子群的算法。刘娟等^[14]提出了结合特征学习的粒子群求解极小碰集方法, 该算法把离散问题转化为连续问题来求解, 而且在合理的时间内能够求出绝大多数的极小碰集。在最小碰集求解问题中, 完备算法可以通过限定搜索树的搜索层数来求解此问题, 而对于不完备算法, 可以通过求解极小碰集后得到其对应的最小碰集。

在不完备求解方法中, 有很多的局部搜索^{[2, 3]}和群智能优化算法都取得了不错的效果。其中GRASP算法在一些规模较大、领域知识较少、较难解决的问题上表现出高效的性能。GRASP算法主要分为构造和局部搜索两个阶段。在构造阶段, 一个可行解被迭代地构造出来, 一旦构造阶段结束, 说明找到了一个局部最优解。然后在局部搜索阶段试图改进这个局部最优解。这两个阶段迭代地执行, 直到到达终止条件。本文提出基于GRASP算法的GPHS求解碰集方法。更重要地, 本文提出了新的部件属性— — 部件动态变化度d-covered和d-rcovered来指导碰集求解。利用d-covered动态打分机制指导当前解中的部件选择, 进而更加预测性地选择那些对以后构造阶段影响更大的部件加入到当前解中; 而候选组件列表使得构造阶段可以更贪心、多样化地选择部件。随后本文基于d-rcovered锦标赛选择策略更有效地删除部分冗余部件, 进而找到该碰集对应更短长度的极小碰集。实验结果表明:本文方法与现有算法相比具有较好的效率, 能在较短时间内得到最优解。

定义1^[4] 一个系统定义为三元组(SD, COMPS, OBS):SD为系统描述; COMPS为系统的组成部件集合; OBS为观测集。

定义2^[4] 关于系统(SD, COMPS, OBS)的冲突集是COMPS的一个子集cfs={c₁, c₂, …, c_n}, 使得SD∪ OBS∪ {¬ AB(c₁), ¬ AB(c₂), …, ¬ AB(c_n)}不一致, AB(· )定义为“ 不正常” 。一个冲突集是极小冲突集, 当且仅当该极小冲突集的任何真子集都不是冲突集。

定义3^[4] 碰集HS为集合蔟SS的一个碰集, 若碰集HS满足:HS⊆∪ _{S∈ SS}S; 对于任意一个S∈ SS, 该碰集与S有交集, HS∩ S≠ ⌀。一个碰集是极小碰集, 当且仅当该极小碰集的任何真子集都不是碰集。

定理1^[4]Δ 是系统的一个极小诊断, 当且仅当Δ 是该系统的所有极小冲突集的极小碰集。

定义4 在所有极小碰集集合中, 最小碰集MLHS是含有部件数量最少的极小碰集。

本文算法中, CS表示部件集合的子集, 即当前解集合。

定义5 一个碰集中存在某个部件, 一些极小冲突集包含该部件, 且所有这些冲突集与这个碰集相交部件个数大于1, 则此部件称为冗余部件。

定理2 若当前解集合是碰集, 那么从当前解集合中删除冗余部件, 该解集合仍然为碰集。

证明 设当前解集合为CS, 其中部件c在J个极小冲突集{cfs₁, cfs₂, …, cfs_J}中出现, 且|CS∩ cfs_i|≥ 2, 其中1≤ i≤ J。若设置CS=CS/{c}, 则|CS∩ cfs_i|≥ 1, 且对部件c不在的其他冲突集, 不影响CS与其相交部件的数量, 即相交部件数大于等于1。通过以上论述, 当删除c后, CS与所有冲突集相交元素都大于等于1, 则CS仍为碰集。

证毕。

定义6 部件动态变化度d-covered(c)的取值为该部件c加入到CS(CS=CS∪ {c})后, 从覆盖d-1个CS中的部件变为覆盖d个CS中的部件时的极小冲突集个数Num, 即d-covered(c)=Num。

例1 CFS={{A, B}, {B, C}, {B, D}}, 当前解CS={A}, 当加入部件B到CS中, 即CS={A, B}。1-covered(B)=2, 因为{B, C}, {B, D}从覆盖0个CS中的部件变为覆盖1个CS中的部件。同理可得, 2-covered(B)=1。

同样地, 本文给出相似的部件动态变化度d-rcovered的定义。

定义7 一个部件c的d-rcovered定义为当该部件从当前解中删除时, 从覆盖d+1个CS中的部件变为只覆盖d个部件时的极小冲突集个数Num, 即d-rcovered(c)=Num。

例2 CFS={{A, B}, {B, C}, {B, D}}, 当前解CS={A, B, D}, 当把部件B从CS中删除, 即CS=CS/{B}={A, D}。1-rcovered(B)=2, 即极小冲突集{A, B}和{B, D}从2覆盖变为1覆盖。同样地, 0-rcovered(B)=1。

定义8 每一个部件c都有各自的打分score(c)。定义如下:

(1)当CS=CS∪ {c}, 有:

score(c)=1-rcovered(c)+OtT×2-covered(c)

式中:OtT为参数, 0≤ OtT≤ 1

(2)当CS=CS/{c}, 有:

rscore(c)=1-rcovered(c)

定义9 在算法构造阶段, 对每一个部件进行打分, 然后选择分数最高的几个放到候选组件列表CCL中, CCL列表中score的最低取值为LCCL× max(score), 其中LCCL为候选组件列表长度的参数, max(score)为打分最高部件的分数。

本文算法在构造阶段利用2-covered的打分机制选择一些具有较高score的部件, 将其放到候选组件列表中, 之后在其中随机地选择一个组件加入到CS中。构造阶段迭代执行, 直到找到一个碰集。而在算法局部搜索阶段, 利用定理2对构造阶段找到的当前解CS, 首先找到当前解中所有的冗余部件, 即0-rcovered等于0的部件; 然后根据这些部件1-rcovered的取值, 利用锦标赛策略选择部件, 该策略定义如下。

定义10 对于K个冗余部件, 锦标赛策略根据这些部件的1-rcovered取值定义这些部件的选择概率。将这K个冗余部件按照从大到小排序, 选择概率pos(c)/(K+1), 其中pos(c)为排序中部件c的位置。

对于对当前解CS影响较小的部件, 即1-rcovered取值较小的部件, 被选择的概率较高, 这样可以当每次找到冗余部件并从当前解中删除时, 使得更少的极小冲突集与当前解CS相交部件数变为1。这样可以删除更多的冗余部件, 使得当前解具有更小长度的极小碰集。而根据1-rcovered的取值概率地选择锦标赛策略, 可以在局部搜索阶段多样化地找到不同的极小碰集, 更有利于寻找最小碰集。

算法1 GPHS

Input:CFS={cfs₁, cfs₂, …, cfs_M}

Output:solution_best_size

Begin

1.solution_best_size=MAX_NUMBER; /* 初始化solution_best_size * /

2.iter=0; /* 初始化iter* /

3.while(iter!=MAX_ITER)

4. CS=ConstructSolution(); /* 构造阶段 * /

5. CS=LocalSearch(); /* 局部搜索阶段 * /

6. if(solution_best_size> CS_size) /* 更新全局最优长度 * /

7. solution_best_size=CS_size;

8. end if

9. iter++;

10.end while

return solution_best_size;

End

上面是GPHS的基本框架, 主要循环是从第3行到第9行。在循环中, 首先随机贪心地构造出一个碰集CS(第4行); 然后当前解会利用局部搜索阶段(第5行), 得到一个更小长度的极小碰集。在每一次循环的最后, 本文算法会判断是否找到了一个解(CS_size)比全局最优解(solution_best_size)更好, 若找到这样的解, 则更新全局最优解(第6行和第7行)。当迭代次数到达终止的最大迭代次数(MAX_NUMBER)时, GPHS返回所求的全局最优解(第11行)。

2.3 算法时间复杂度

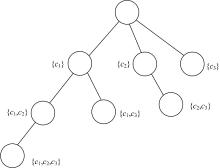
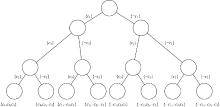
通过修改基于树的完备算法可以用来求解最小碰集, 本节分析完备算法和不完备算法的时间复杂度。下面给出完备算法对应等价的部件枚举树和部件二叉树。图1为部件数为3的部件枚举树。图2是部件数为3的部件二叉树。

由图1可知, 枚举树通过搜索所有的子节点和叶节点来求解极小碰集。在此基础上, 可以通过限定层的深度来优化求解过程, 进而求解最小碰集。 而由图2可知, 对于基于二叉树的完备求解算法, 需要通过搜索所有的叶节点来寻找极小碰集。与枚举树不同之处是基于二叉树的完备算法不能通过限定层数来优化求解最小碰集。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 部件集为{c1, c2, c3}的部件枚举树Fig.1 Enumeration tree with {c1, c2, c3}

基于树的完备求解算法的求解时间会随着实例的部件数量和冲突集数量的增大呈指数级增加。对于完备算法, 若部件个数为N, 那么整个解空间大小为2^N。虽然采用了一些剪枝或者其他优化策略, 但是搜索的空间仍不能降低到线性级别。但对于本文提出的GPHS算法:在构造阶段, 所需搜索的最大解空间为N; 在局部搜索阶段, 所需搜索的解空间大小为N× SIZE, 其中SIZE为当前解的长度。在iter次迭代后, 最大搜索的解空间大小为iter× N(1+SIZE)。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 部件集为{c1, c2, c3}的部件二叉树Fig.2 Binary tree with {c1, c2, c3}

对GPHS算法实验结果进行分析, 并与PSO算法^[14]、CHS-Tree算法^[10]进行比较。本文算法运行环境为Linux, 2.1 GHz Intel Core2 CPU E7400, 内存为4 GB, 编程语言为C++。算法使用gcc编译器, 并使用-O2进行优化。本文选用的测试用例定义如下:V30S25, 部件个数为30, 极小冲突集个数为25。本文选用的测试用例中, 单个部件在每一个极小冲突集中的出现概率为p。为了对本文算法的有效性和求解效率分别进行分析, 选取不同规模的数据进行实验。

在本文算法中, 参数设置如下:OtT为0.1, LCCL为0.9。GPHS的迭代次数iter为10 000, 对于对比的PSO算法设种群数为10, 迭代次数为10 000。

首先选用10个规模较小的实例, 并与出色的完备算法CHS-Tree进行对比, 测试用例部件的出现概率p=20%, 部件和冲突集个数见表1。

表1

Table 1

表1(Table 1)

表1 GPHS和CHS-Tree的实验结果 Table 1 Results of GPHS and CHS-Tree Instance CHS-Tree GPHS Length STime/s Length STime/s FTime/s v25s20 6 0.07 6 0.01 0.17 v25s25 6 0.34 6 0.01 0.21 v25s30 6 0.35 6 0.01 0.22 v25s35 7 0.09 7 0.01 0.30 v30s20 4 20.64 4 0.01 0.13 v30s25 6 16.19 6 0.01 0.25 v30s30 6 39.69 6 0.01 0.28 v30s35 6 17.60 6 0.01 0.36 v35s20 5 157.81 5 0.01 0.19 v35s25 5 1022.67 5 0.01 0.28

表1 GPHS和CHS-Tree的实验结果 Table 1 Results of GPHS and CHS-Tree

表1中, Length为两种算法求解出的极小碰集的最小长度; STime为求解出最小长度的时间; FTime为GPHS算法到达最大迭代次数的结束时间。从表1可得, GPHS算法在规定的迭代次数中都可以得到与CHS-Tree算法相同的最小长度极小碰集, 表明了本文算法的有效性。

本文还对以下实验用例进行了测试。选取部件个数为30、冲突集个数为30, 部件出现概率p从0.1到0.9, 总共选取9个测试用例。分别用两种算法对每一个测试用例求解10次, 得到平均长度avgL, 同时给出两种算法迭代结束后的最终平均时间avgFT。实验结果如表2所示。

表2

Table 2

表2(Table 2)

表2 GPHS和PSO在V30S30下的实验结果 Table 2 Experimental results of GPHS and PSO on V30S30 p/% Length GPHS算法 PSO算法 avgL avgFT/s avgL avgFT/s 10 10 10 0.27 15.6 0.08 20 6 6 0.27 7.3 0.08 30 4 4 0.27 5.1 0.08 40 3 3 0.27 3.6 0.08 50 3 3 0.27 3 0.08 60 3 3 0.27 3 0.08 70 2 2 0.27 2 0.08 80 2 2 0.27 2 0.08 90 1 1 0.27 1 0.08

表2 GPHS和PSO在V30S30下的实验结果 Table 2 Experimental results of GPHS and PSO on V30S30

从表2可知, 随着概率p的增大, 极小碰集的最小长度减少。两种算法的最终时间都不随着概率p的改变而改变。在相同的迭代次数下, PSO算法的运算时间比本文算法略好, 概率p大于40%时, 两种算法都能求出最小长度。但当部件的出现概率小于等于40%时, GPHS算法仍能求出所有的最小长度, 而且运行10次均能得到解。然而, PSO算法在一些时候不能得到最优解, 表现出不稳定性。PSO算法是基于粒子群的改进方法, 该方法适用于快速地求解出大部分极小碰集的情况, 属于广度搜索。而本文算法是基于GRASP的改进算法, 该算法适用于深度搜索, 即找出一些具有特定特征的极小碰集。通过表1和表2可知, 对于求解最小长度的极小碰集问题, 本文算法表现出很好的稳定性, 在求解时间上, 也可以快速地找到最优解。

表3中, 测试用例的概率p为20%。GPHS+N2C算法表示计算每一个部件打分的时候不包含2-covered, 即score=1-covered。GPHS算法中, score=1-covered+OtT× 2-covered。当求得长度为Length的极小碰集时, CurIter表示此时已进行的迭代次数。部件和冲突集规模都较大时, 对2-covered进行了性能分析。由表3的实验结果可以看出, GPHS算法因为使用了2-covered这个属性, 更能找到最优解。如v500s1000和v1000s500, GPHS算法分别找到了最小长度为14和11的极小碰集, 都好于GPHS+N2C找到的解。对于其他测试用例, 两种算法都找到相同大小的解, 但是GPHS算法使用的迭代次数明显较少。

表3

Table 3

表3(Table 3)

表3 GPHS和GPHS+N2C的实验结果 Table 3 Experimental Results of GPHS and GPHS+N2C Instance GPHS算法 GPHS+N2C算法 CurIter Length CurIter Length v100s100 1 8 16 8 v100s500 515 13 782 13 v100s1000 932 15 1072 15 v500s100 212 6 212 6 v500s500 44 12 44 12 v500s1000 240 14 8 15 v1000s100 18 6 894 6 v1000s500 10 11 8 12

表3 GPHS和GPHS+N2C的实验结果 Table 3 Experimental Results of GPHS and GPHS+N2C

针对极小碰集问题中的最小碰集问题, 提出了结合部件动态变化度的GRASP求解最小碰集算法。首次提出部件动态变化度的概念, 利用此属性指导新算法的构造阶段和局部搜索阶段。在构造阶段, 利用d-covered对部件进行打分, 根据1-covered贪心地选择未覆盖极小冲突集较多的部件, 再依据2-covered选择尽可能多的冗余部件来保证解空间的多样性, 进而避免陷入局部最优。在局部搜索阶段, 0-rcovered取值为0的是冗余部件, 然后利用锦标赛策略, 根据1-rcovered的取值对冗余部件进行概率排序, 在保证多样性的前提下概率地选择删除冗余部件, 并尽可能较早找到最小碰集。本文还从稳定性和高效性两方面对GPHS算法进行实验测试分析, 与完备算法CHS-Tree相比, GPHS算法可以在较短时间内得到最优解; 与不完备算法PSO算法相比, GPHS算法可以发现具有更短长度的最小碰集, 且运行时间上与PSO算法相近。在未来的工作中, 将尝试结合其他高效的搜索方法^{[15, 16]}更加高效地求解此问题。