随着大数据时代的来临, 实际工程中的计算模型越来越复杂, 如何选取最优参数以获得更高精度的结果是复杂系统建模领域的关键问题, 优化算法则是解决这类问题的有力工具。目前, 优化算法主要可以分为两大类:①以数学手段为基础的经典优化算法, 包括单纯形法^[1]、最速下降法^[2]、牛顿法^[3]及序列二次规划法^[4]等。②受自然界启发的智能优化算法, 包括模拟退火算法^[5]、遗传算法^[6]、粒子群算法^[7]、鱼群算法^[8]、蚁群算法^[9]及差分进化算法^[10]等。

经典优化算法的计算过程复杂, 并且对目标函数的性质有着严格的要求, 因此不适用于解决高维复杂的优化问题。智能优化算法实现简单, 对求解问题没有严格要求, 仅以目标函数值作为适应度值, 因而比经典优化算法的应用更加广泛。智能优化算法是以一组随机的解作为初始种群, 通过迭代不断地搜索最优解。由于在迭代的过程中, 为种群引入了“ 交流” 、“ 学习” 等智能行为, 所以智能优化算法中的搜索是带有启发式的, 是群体智能涌现的过程。但是, 智能优化算法也存在一些不足之处:①当优化复杂多峰值函数时, 大多智能优化算法都容易陷入局部最优解。②当求解高维优化问题时, 由于解空间随着维度的增大而迅速扩张, 大多智能优化算法无法在有限的时间内收敛至全局最优解。

针对上述问题, 已有很多文献提出了改进方法。例如, 利用模糊理论和混沌理论控制种群的进化^{[11, 12]}; 将小生境技术引入种群的进化^[13]; 采用量子原理进行最优解的搜索^[14]以及结合多种算法的混合优化技术^[15]。这些改进的方法从不同层面上提高了优化算法的全局搜索能力, 但是由于过多地强调全局搜索, 而使它们在优化一些高维复杂多峰值函数时都存在局部搜索精度不高的问题。

协方差矩阵自适应进化策略(CMA-ES)算法是目前比较先进的全局优化算法^[16], 它由Hansen首次提出, 并在近期的IEEE Congress on Evolutionary Computation的进化算法排名中表现优异^[17]。本文将混沌理论引入CMA-ES算法, 提出了混沌协方差矩阵自适应进化策略(Chaos-CMA-ES)算法。该算法利用混沌方程构建混沌算子并更新种群的中心期望值。混沌算子产生的解具有更好的遍历性, 可以辅助种群向全局最优解进化。实验结果和网络安全态势预测案例都表明, Chaos-CMA-ES算法具有良好的全局搜索能力和实用价值。

CMA-ES算法的本质属于进化策略类算法, 它被用来解决复杂的非线性、非连续的凸优化问题。CMA-ES算法的基本操作可以分为3部分:

(1)采样操作。CMA-ES算法首先在解空间中随机选择一个解, 然后以这个解为中心点利用正态分布生成种群, 如式(1)所示:

xig+1~mg+σgN(0, Cg)i=1, 2, …, λ(1)

式中:x_i为种群中第i个个体; λ 为种群大小; g为进化代数; m为种群的中心点(也称期望); σ 为步长; N表示多元正态分布; C为种群的协方差矩阵。

按照上述多元正态分布生成的种群, 其等密度曲面是一个超椭球体。式(1)中的协方差矩阵C是CMA-ES算法的关键元素, C的特征向量对应于种群分布椭球的长轴; C的特征值等于长轴长度的平方。初始的C可以设置为一个D× D的单位矩阵, 其中D为解的维度。

(2)选择和重组操作。该操作会在生成的种群中选择一部分最优解作为子种群。新的种群期望值如式(2)所示:

mg+1=∑i=1μwixi:λg+1(2)

式中:μ 为子种群大小; w_i为依据适应度值设置的权重, 各权重的和为1; x_i:λ 为在种群中λ 个个体中选择出的第i个个体。

式(2)表明, 下一代种群分布的中心将向子种群偏移, 且靠近其中的最优解。

(3)更新操作。该操作主要用来更新种群的协方差矩阵, 使其可以引导整个种群去搜索全局最优解。更新操作结合了两种截然不同的工作模式:Rank-μ -update和Rank-1-update^[18], 前者使用了μ 个个体相对期望之间的偏差, 后者使用了相邻两代期望之间的偏差。更新过程如式(3)所示:

Cg+1=1-c1-cμCg+c1pcg+1pcg+1T+cμ∑i=1μwiyi:λg+1yi:λg+1T（3）

式中:等式右边求和的第2部分为Rank-1-update模式, 第3部分为Rank-μ -update模式; c₁和c_μ 分别为上述两种不同更新模式下的学习率, c₁≈ 2/D², c_μ ≈ min(μ _eff/D², 1-c₁), μ _eff为方差影响选择集^[19], 可以由式(4)得出:

μeff=∑i=1μwi2-1（4）

yi:λg+1=( xi:λg+1-m^g)/σ ^g; p_c为协方差矩阵的进化路径, 初始p_c等于0, 其更新过程如式(5)所示:

pcg+1=1-ccpcg+cc2-ccμeff(mg+1-mg)/σg](5)

式中:c_c为进化路径p_c的学习率。

式(5)中的步长σ 也需要更新, 如式(6)所示:

σg+1=σgexpcσdσ‖pσg+1‖E‖N0, I‖-1(6)

式中:E(· )为求数学期望函数; I为单位矩阵; c_σ 为步长的学习率; d_σ 为步长更新的阻尼系数; p_σ 为步长的进化路径, 初始p_σ 等于0, 其更新方式为:

pσg+1=1-ccpσg+cσ2-cσμeffCg-12(mg+1-mg)/σg](7)

上述CMA-ES公式中的参数大都是自含的, 当初始参数设置好后, CMA-ES算法会按照上面的操作迭代循环, 逐步搜索全局最优解。

本文在原始CMA-ES算法的基础上, 提出了一种结合混沌理论的CMA-ES算法, 称为Chaos-CMA-ES算法。该算法在原算法的选择操作之后加入了混沌算子, 使得新的种群期望能够以更大的概率靠近全局最优解, 有效地防止了种群陷入到局部最优解中。

为了测试Chaos-CMA-ES算法的性能, 设计了比较实验。选取了3种流行的优化算法与本文算法进行比较, 其中包括原始的CMA-ES算法、粒子群(PSO)算法以及差分进化(DE)算法。比较实验所用到的10个典型的基准测试函数取自优化算法标准测试函数集, 且都是复杂多峰值函数或极难搜索到全局最优解的平坦函数, 其特性如表1所示, 其中各个函数的表达式可参考相关文献[20], 比较结果如表2、表3、表4所示。

表1

Table 1

表1(Table 1)

表1 测试函数 Table 1 Testing functions 标号 函数名 解空间范围/D 特性 f1 Ackley Function [-40, 40] 多峰 f2 Generalized Schwefel's Problem 2.26 [-500, 500] 多峰 f3 Generalized Griewank Function [-600, 600] 多峰 f4 Bohachevsky Function [-2, 2] 多峰 f5 Trigonometric02 Function [0, 2] 多峰 f6 Yao-Liu function [-0.1, 3] 多峰 f7 Generalized Rosenbrock's Function [-40, 40] 多峰 f8 Weierstrass Function [-0.5, 0.5] 多峰 f9 Schwefel's Problem 1.2 Noise [-100, 100] 加噪 f10 Dixon and Price Function [-10, 10] 平坦

表1 测试函数 Table 1 Testing functions

在以上这些函数中, f₁~f₈为复杂的多峰函数, 在它们的解空间范围内存在多个极值, 且极值之间差异不大, 一般算法很容易陷入到局部最优解中。f₉为加噪测试函数, f₁₀为平坦函数, 一般算法在这两类问题上也很难搜索到全局最优解, 因为算法在优化加噪测试函数时容易受到噪声的干扰, 在优化平坦函数时容易陷入停滞。

表2

Table 2

表2(Table 2)

表2 本文算法与其他算法在10维上的比较结果 Table 2 Comparative results in 10 dimension 函数 结果 算法 Chaos- CMA-ES CMA-ES PSO DE f1 Best 5.87× 10-8 6.11× 10-8 1.99× 101 2.66× 100 Worst 9.95× 10-8 1.99× 100 2.09× 101 2.66× 100 Mean 8.54× 10-8 1.71× 101 2.00× 101 2.66× 100 Std 1.16× 10-8 6.67× 100 0.47× 100 0.00× 100 FES 5.45× 104 9.04× 104 1.00× 105 1.00× 105 f2 Best 3.57× 10-8 1.27× 103 1.04× 103 4.19× 103 Worst 7.60× 10-8 2.72× 103 1.04× 103 4.19× 103 Mean 5.89× 10-8 1.96× 103 1.04× 103 4.19× 103 Std 2.17× 10-8 3.56× 102 0.00× 100 0.00× 100 FES 4.82× 105 1.00× 106 7.25× 105 2.74× 106 f3 Best 4.73× 10-8 6.65× 10-8 6.16× 10-1 2.14× 10-1 Worst 2.46× 10-2 3.94× 10-2 7.86× 10-1 3.37× 10-1 Mean 1.06× 10-2 1.60× 10-2 7.01× 10-1 2.75× 10-1 Std 7.80× 10-3 1.25× 10-2 6.43× 10-1 6.15× 10-2 FES 8.90× 105 9.05× 105 8.24× 106 1.12× 106 f4 Best 6.01× 10-8 6.57× 10-8 1.05× 100 9.64× 10-8 Worst 8.36× 10-1 1.46× 100 1.05× 100 9.64× 10-8 Mean 1.17× 10-1 2.76× 10-1 1.05× 100 9.64× 10-8 Std 2.74× 10-1 4.64× 10-1 1.05× 100 0.00× 100 FES 2.87× 104 4.34× 104 1.00× 105 1.22× 104 f5 Best 8.74× 10-8 9.60× 10-8 8.78× 100 9.16× 10-8 Worst 8.67× 100 9.35× 100 8.78× 100 9.16× 10-8 Mean 2.79× 100 6.28× 101 8.78× 100 9.16× 10-8 Std 3.03× 100 3.78× 101 0.00× 100 0.00× 100 FES 1.00× 105 1.00× 105 1.00× 105 1.07× 104 f6 Best 0.00× 100 0.00× 100 0.00× 100 7.98× 10-8 Worst 0.00× 100 1.31× 100 1.54× 10-1 7.98× 10-8 Mean 0.00× 100 2.28× 10-1 8.34× 10-2 7.98× 10-8 Std 0.00× 100 4.69× 10-1 6.73× 10-2 0.00× 100 FES 2.39× 104 3.11× 104 1.00× 107 3.30× 104 f7 Best 6.85× 10-8 8.50× 10-8 2.90× 10-5 9.24× 10-8 Worst 9.52× 10-8 3.99× 100 2.90× 10-5 9.84× 10-8 Mean 8.40× 10-8 7.97× 10-1 2.90× 10-5 9.24× 10-8 Std 7.74× 10-9 1.68× 100 0.00× 100 0.00× 100 FES 1.00× 105 1.00× 105 8.84× 106 1.91× 104 f8 Best 6.52× 10-8 8.57× 10-8 1.23× 101 8.78× 10-8 Worst 9.39× 10-8 1.58× 10-1 1.23× 101 8.78× 10-8 Mean 7.38× 10-8 1.59× 10-2 1.23× 101 8.78× 10-8 Std 1.35× 10-8 5.00× 10-2 0.00× 100 0.00× 100 FES 3.36× 104 4.44× 104 1.00× 105 1.00× 105 f9 Best 2.82× 10-8 4.93× 10-8 3.22× 10-5 8.72× 10-8 Worst 9.13× 10-8 1.37× 103 3.22× 10-5 8.72× 10-8 Mean 6.87× 10-8 1.78× 102 3.22× 10-5 8.72× 10-8 Std 1.95× 10-8 4.33× 102 0.00× 100 0.00× 100 FES 4.51× 104 5.55× 104 1.00× 106 1.00× 105 f10 Best 6.67× 10-1 6.67× 10-1 2.35× 10-5 6.67× 10-1 Worst 6.67× 10-1 6.67× 10-1 2.35× 10-5 6.67× 10-1 Mean 6.67× 10-1 6.67× 10-1 2.35× 10-5 6.67× 10-1 Std 0.00× 100 0.00× 100 0.00× 100 0.00× 100 FES 1.00× 104 1.00× 104 1.37× 106 1.00× 104

表2 本文算法与其他算法在10维上的比较结果 Table 2 Comparative results in 10 dimension

表3

Table 3

表3(Table 3)

表3 本文算法与其他算法在30维上的比较结果 Table 3 Comparative results in 30 dimension 函数 结果 算法 Chaos- CMA-ES CMA-ES PSO DE f1 Best 7.58× 10-8 8.04× 10-8 2.00× 101 2.68× 100 Worst 9.98× 10-8 2.00× 101 2.00× 101 2.75× 100 Mean 9.27× 10-8 1.78× 101 2.00× 101 2.71× 100 Std 6.41× 10-9 6.03× 100 0.00× 100 0.18× 100 FES 1.08× 105 1.28× 105 1.50× 105 1.50× 105 f2 Best 8.35× 10-8 5.06× 103 1.44× 103 1.26× 104 Worst 9.63× 10-8 6.34× 103 1.44× 103 1.26× 104 Mean 8.56× 10-8 5.64× 103 1.44× 103 1.26× 104 Std 9.42× 10-9 4.78× 102 0.00× 100 0.00× 100 FES 1.37× 106 1.50× 106 2.37× 107 8.41× 107 f3 Best 7.21× 10-8 8.56× 10-8 2.55× 10-5 5.42× 100 Worst 9.80× 10-8 9.90× 10-3 1.10× 10-4 5.42× 100 Mean 8.90× 10-8 2.50× 10-3 1.86× 10-4 5.42× 100 Std 1.05× 10-8 4.00× 10-3 3.67× 10-5 0.00× 100 FES 1.49× 105 1.51× 105 1.75× 107 1.14× 106 f4 Best 4.93× 10-4 4.13× 10-1 3.20× 100 4.98× 100 Worst 4.93× 10-4 4.13× 10-1 3.20× 100 4.98× 100 Mean 4.93× 10-4 4.13× 10-1 3.19× 100 4.98× 100 Std 0.00× 100 0.00× 100 0.00× 100 0.00× 100 FES 9.98× 104 1.00× 105 1.26× 106 1.43× 106 f5 Best 2.19× 10-1 4.49× 10-1 8.13× 101 6.26× 100 Worst 1.61× 100 3.60× 100 8.13× 101 6.26× 100 Mean 9.12× 10-1 1.89× 100 8.13× 101 6.26× 100 Std 8.29× 10-1 1.20× 100 0.00× 100 0.00× 100 FES 1.20× 105 4.20× 105 2.38× 106 3.20× 106 f6 Best 0.00× 100 0.00× 100 4.84× 101 5.48× 102 Worst 2.02× 100 8.73× 100 4.84× 101 5.48× 102 Mean 0.20× 10-1 0.87× 10-1 4.84× 101 5.48× 102 Std 6.38× 10-1 3.30× 10-1 0.00× 100 0.00× 100 FES 7.35× 105 1.00× 106 1.00× 107 1.00× 107 f7 Best 7.64× 10-8 8.62× 10-8 2.26× 101 1.13× 104 Worst 9.92× 10-8 9.78× 10-8 2.88× 101 3.48× 104 Mean 8.60× 10-8 8.99× 10-8 2.53× 101 3.24× 104 Std 7.47× 10-9 9.77× 10-9 2.55× 100 5.69× 103 FES 8.12× 105 8.03× 105 3.72× 106 1.36× 106 f8 Best 4.35× 10-2 2.64× 100 4.59× 101 6.23× 100 Worst 2.53× 100 2.64× 100 4.59× 101 6.23× 100 Mean 1.25× 10-2 2.64× 100 4.59× 101 6.23× 100 Std 6.35× 10-1 0.00× 100 0.00× 100 0.00× 100 FES 1.00× 106 1.00× 106 1.00× 106 1.00× 106 f9 Best 9.28× 10-8 2.97× 101 4.54× 10-1 6.75× 102 Worst 6.98× 10-1 1.93× 103 4.54× 10-1 6.75× 102 Mean 1.77× 10-1 8.16× 103 4.54× 10-1 6.75× 102 Std 3.49× 10-1 8.83× 103 0.00× 100 0.00× 100 FES 1.28× 106 1.00× 106 3.00× 106 1.00× 106 f10 Best 6.67× 10-1 6.67× 10-1 6.67× 10-1 7.80× 10-1 Worst 6.67× 10-1 6.67× 10-1 6.67× 10-1 7.80× 10-1 Mean 6.67× 10-1 6.67× 10-1 6.67× 10-1 7.80× 10-1 Std 0.00× 100 0.00× 100 0.00× 100 0.00× 100 FES 1.00× 104 1.00× 104 1.00× 105 1.00× 104

表3 本文算法与其他算法在30维上的比较结果 Table 3 Comparative results in 30 dimension

表4

Table 4

表4(Table 4)

表4 本文算法与其他算法在50维上的比较结果 Table 4 Comparative results in 50 dimension 函数 结果 算法 Chaos- CMA-ES CMA-ES PSO DE f1 Best 8.85× 10-8 1.98× 101 1.99× 101 2.72× 100 Worst 9.99× 10-8 1.99× 101 1.99× 101 2.73× 100 Mean 9.71× 10-8 1.98× 101 1.99× 101 2.72× 100 Std 2.89× 10-9 3.12× 10-2 0.00× 100 1.56× 10-1 FES 1.46× 105 7.50× 105 7.50× 105 7.50× 105 f2 Best 7.59× 10-8 9.17× 103 6.24× 103 2.10× 104 Worst 9.64× 10-8 9.17× 103 6.24× 103 2.10× 104 Mean 8.83× 10-8 9.17× 103 6.24× 103 2.10× 104 Std 1.59× 10-9 0.00× 100 0.00× 100 0.00× 100 FES 1.77× 107 1.83× 107 8.57× 107 8.41× 107 f3 Best 8.83× 10-8 9.24× 10-8 8.50× 10-2 2.65× 101 Worst 7.40× 10-3 1.48× 10-2 8.50× 10-2 2.65× 101 Mean 7.40× 10-4 1.50× 10-3 8.50× 10-2 2.65× 101 Std 2.30× 10-3 4.70× 10-3 0.00× 100 0.00× 100 FES 1.02× 106 1.34× 106 3.85× 107 6.43× 106 f4 Best 3.15× 100 3.62× 100 7.83× 100 1.47× 101 Worst 3.15× 100 3.62× 100 7.83× 100 1.47× 101 Mean 3.15× 100 3.62× 100 7.83× 100 1.47× 101 Std 0.00× 100 0.00× 100 0.00× 100 0.00× 100 FES 1.00× 105 1.00× 105 1.00× 106 1.00× 106 f5 Best 2.70× 100 5.00× 100 1.13× 102 2.38× 101 Worst 2.70× 100 5.00× 100 1.13× 102 2.38× 101 Mean 2.70× 100 5.00× 100 1.13× 102 2.38× 101 Std 0.00× 100 0.00× 100 0.00× 100 0.00× 100 FES 1.20× 105 1.20× 105 2.10× 106 2.16× 105 f6 Best 0.00× 100 0.00× 100 2.21× 102 7.89× 103 Worst 5.19× 100 1.77× 101 2.21× 102 7.90× 103 Mean 2.35× 10-1 1.67× 100 2.21× 102 7.89× 103 Std 7.60× 10-1 5.77× 10-1 0.00× 100 0.00× 100 FES 1.00× 106 1.00× 106 1.00× 107 1.00× 107 f7 Best 7.77× 10-8 8.84× 10-8 4.47× 101 2.89× 105 Worst 3.99× 100 3.99× 100 9.57× 101 1.49× 106 Mean 9.97× 10-1 9.99× 10-1 5.65× 101 7.84× 105 Std 1.99× 100 1.26× 100 2.20× 101 3.25× 105 FES 3.46× 106 4.02× 106 1.81× 106 1.29× 106 f8 Best 1.55× 10-1 5.80× 100 8.28× 101 7.38× 100 Worst 8.55× 100 5.80× 100 8.28× 101 7.38× 100 Mean 2.36× 100 5.80× 100 8.28× 101 7.38× 100 Std 9.67× 10-1 0.00× 100 0.00× 100 0.00× 100 FES 1.00× 106 1.00× 106 1.00× 106 1.00× 106 f9 Best 6.61× 102 1.35× 104 9.44× 104 1.43× 105 Worst 1.13× 103 1.35× 104 9.44× 104 1.43× 105 Mean 8.86× 102 1.35× 104 9.44× 104 1.43× 105 Std 2.54× 102 0.00× 100 0.00× 100 0.00× 100 FES 1.00× 106 1.00× 106 1.00× 106 1.00× 106 f10 Best 6.67× 10-1 6.67× 10-1 8.87× 10-1 3.57× 100 Worst 6.67× 10-1 6.67× 10-1 8.87× 10-1 3.57× 100 Mean 6.67× 10-1 6.67× 10-1 8.87× 10-1 3.57× 100 Std 0.00× 100 0.00× 100 0.00× 100 0.00× 100 FES 1.00× 104 1.00× 104 1.00× 105 1.00× 104

表4 本文算法与其他算法在50维上的比较结果 Table 4 Comparative results in 50 dimension

参与比较的算法在上述测试函数上独立运行30次, 维度分别取10、30和50。表2~表4中Best表示30次实验中的最好结果; Worst表示30次实验中最坏结果; Mean表示30次实验的平均结果; Std表示统计结果中的标准差, 代表了每次结果之间的偏差; FES表示平均评价次数, 即在搜索最优解时算法调用目标函数的平均次数。

从表2、表3、表4可以看出:本文所提出的Chaos-CMA-ES算法在大多数的测试函数和维度中表现优异, 其统计结果要好于其他算法, 且消耗的运算代价也相对较低, 表明了本文方法的有效性。

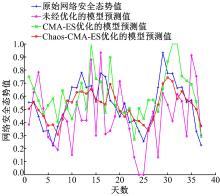
为了进一步证明本文算法的实用性, 在本案例中利用Chaos-CMA-ES算法优化网络安全态势预测模型的参数^{[21, 22, 23, 24]}。预测模型采用RBF神经网络。案例收集了某网络平台120天的网络安全态势值, 如图1所示, 其中前80天作为训练数据, 后40天作为测试数据。预测结果如图2所示。

在图2所示的网络安全态势预测结果中, 没有经过优化的原始RBF模型的预测精度为0.0641; 经CMA-ES优化的RBF模型预测精度为0.0342; 经Chaos-CMA-ES优化的RBF模型预测精度为0.0104, 可见Chaos-CMA-ES算法提升了网络安全态势预测模型的精度, 具有一定的实用价值。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 所收集的120天网络安全态势值Fig.1 Network security situation collected during 120 days

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 网络安全态势值预测结果比较Fig.2 Comparative results of network security situation prediction

提出了一种结合混沌理论的协方差矩阵自适应进化策略— — Chaos-CMA-ES算法。该算法在选择操作之后执行混沌算子, 使得种群的期望可以跳出局部最优解, 以更高的概率引导种群搜索全局最优解。实验和网络安全态势预测案例表明了本文算法的优势和实用性。