基于计算机视觉和测量平差理论的相机标定

引用本文

王凤艳, 黄润秋, 陈剑平, 张元元, 王明常. 基于计算机视觉和测量平差理论的相机标定. 吉林大学学报(工学版), 2017, 47(3): 944-951
WANG Feng-yan, HUANG Run-qiu, CHEN Jian-ping, ZHANG Yuan-yuan, WANG Ming-chang. Camera calibration based on computer vision and surveying adjustment fundamentals. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 944-951 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703035
Permissions

基于计算机视觉和测量平差理论的相机标定

王凤艳^1,², 黄润秋², 陈剑平³, 张元元⁴, 王明常¹

1.吉林大学地球探测科学与技术学院, 长春 130026

2.成都理工大学地质灾害防治与地质环境保护国家重点实验室, 成都 610059

3.吉林大学建设工程学院, 长春 130026

4.北京市勘察设计研究院有限公司工程检测监测所, 北京 100038

黄润秋(1963-),男,教授,博士生导师.研究方向:工程地质,岩土工程.E-mail:hrq@cdut.edu.cn

作者简介:王凤艳(1970-),女,教授,博士.研究方向:工程测量.E-mail:wangfy@jlu.edu.cn

基金项目:国家自然科学基金项目(41472243,41330636); 地质灾害防治与地质环境保护国家重点实验室开放基金项目(SKLGP2013K018); 区域开发与环境响应湖北省重点实验室开放研究基金项目(2015(B)003)

摘要

以计算机视觉中顾及径向和切向畸变的针孔模型为基础,引入测量平差理论,建立了基于计算机视觉和测量平差理论的相机标定数学模型,并以液晶显示屏棋盘格网作为相机标定参照物,以Microsoft Visual Studio为开发平台,利用MFC结合OpenCV编制了相机标定软件Camera Calibration 1.0。通过对数码相机Canon 5D Marx II的标定试验及与近景摄影测量商业软件Lensphoto的对比试验,得出标定参数的精度在±1 pixel内,验证了所建相机标定模型的正确性和相机标定软件Camera Calibration 1.0的可靠性,且利用所建相机标定模型实现了对标定参数的精度评定,从而克服了传统计算机视觉中只计算像点坐标重投影误差的单一精度评定方法的局限。最后,将研究成果用于长春市杨家沟采石场边坡结构面信息的勘察实践,获取了采石场边坡大量随机结构面的迹线和产状信息,为基于随机动力学的边坡稳定性评价提供了详实的基础数据。研究成果还可用于以非量测相机作为传感器的其他生产及科研工作。

关键词: 计算机应用; 相机标定; 测量平差理论; OpenCV; 棋盘格网; 结构面

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2017)03-0944-08

Camera calibration based on computer vision and surveying adjustment fundamentals

WANG Feng-yan^1,², HUANG Run-qiu², CHEN Jian-ping³, ZHANG Yuan-yuan⁴, WANG Ming-chang¹

1.College of Geo-Exploration Science and Technology, Jilin University, Changchun 130026, China

2.State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China

3.College of Construction Engineering, Jilin University, Changchun 130026, China

4.Institute of Engineering Detecting and Monitoring, Beijing Engineering Corporation Limited, Beijing 100038, China

Abstract

On the basis of the pinhole model with radial and tangential distortions in computer vision, mathematical models of camera calibration based on computer vision and surveying adjustment fundamentals were established. Taking chess grid of Liquid Crystal Display (LCD) as reference object for camera calibration, Microsoft Visual Studio as the development platform, camera calibration software, Camera Calibration 1.0, was programmed based on MFC and OpenCV. Through calibration experiments for Canon 5D Marx II digital camera, and comparison with commercial software Lensphoto of close rang photogrammetry system, it was shown that the errors of calibration parameters were within ±1 pixel, and the correctness of the established camera calibration models was verified. The reliability of the Camera Calibration 1.0 software was validated. The precision evaluation of calibration parameters was achieved using the established calibration models, which overcomes the limit in conventional computer vision that only single precision for projecting errors of image point coordinates was evaluated. Furthermore, the method developed in this study was applied to the discontinuity investigation of the slope of Yangjiagou quarry in Changchun. The information of a large number of random discontinuities of rock mass slop was obtained to provide the full and accurate data for stability evaluation of the slop.

Key words: computer application; camera calibration; surveying adjustment fundamentals; OpenCV; chess grid; discontinuities

Show Figures

0 引言

普通数码相机(非量测相机)的普及及其标定技术的日益成熟, 使其在很多领域发挥量测作用^{[1, 2, 3, 4]}。与量测相机相比, 非量测相机内参数未知且镜头畸变较大, 用于量测作业时需进行标定, 获取内参数和畸变系数, 并根据其对所摄影像进行校正, 校正后的影像才能用于建模量测。非量测相机的标定是数字摄影测量关键技术之一, 它是获取相机像主点坐标(x₀, y₀)、主距(f_x, f_y)、畸变差系数(包括径向畸变、切向畸变等)、像元不正交性(dβ )和比例尺不一致性(ds)等的一个过程^[5]。相机标定的典型方法有计算机视觉方法和摄影测量方法^[6]。计算机视觉中, 有Zhang的平面格网法^[7]和Tsai的两步法^{[8, 9]}; 摄影测量方法有基于二维直接线性变换(2D-DLT)^[10]、基于三维直接线性变换(3D-DLT)和共线方程的光束法平差^{[11, 12, 13]}。从相机标定采用的人造参照物上, 分为室外控制场、室内控制场、简易三维刚体、平面格网、一维物体等^{[14, 15, 16, 17]}。从现有标定方法看, 基于高精度的室外、室内控制场的标定精度高, 但推广难; 基于特制格网板、格网体的标定精度较高, 但很难制造出高精度格网; 基于建筑物垂直线的灭点法较为灵活, 但精度有限。尽管计算机视觉理论及摄影测量理论已经相当成熟, 但如何突破现有一些相机标定方法的局限, 研究方便快捷、灵活适用和较高精度的相机标定方法和软件, 仍值得进一步探讨。

为此, 本文从相机标定可靠性出发, 在借鉴摄影测量方法的基础上, 以计算机视觉中顾及畸变的针孔模型为基础, 结合测量平差理论^[18], 建立了基于计算机视觉和测量平差理论的相机标定数学模型, 实现了标定参数的解算及其精度评定, 克服了传统计算机视觉中只进行像点坐标重投影误差的单一精度评定方法的局限。从相机标定便捷及灵活性出发, 研究了以液晶显示屏棋盘格网作为参照物的相机标定。从标定软件易编制性和易操作性出发, 以Microsoft Visual Studio为开发平台, 利用MFC结合OpenCV编制了标定软件Camera Calibration 1.0^[19], 并与近景摄影测量商业软件Lensphoto相机标定结果进行对比。结果表明:基于计算机视觉和测量平差理论建立的相机标定数学模型, 可以实现相机的快速、高精度标定, 标定误差在± 1 pixel内。

1 待标定参数

1.1 成像模型

计算机视觉中使用针孔摄像机模型, 即一幅视图是通过将三维空间中的点透视变换投影到图像平面上得到。OpenCV标定算法以针孔模型为基础, 引入透镜径向和切向畸变, 使成像模型更加真实地反映透镜的实际畸变情况。建立三维空间点P与其投影到图像平面上的像点p之间关系的过程可分解为4个步骤, 涉及4种坐标系(见图1), 即:物方坐标系O_W-X_WY_WZ_W、相机坐标系O-xyz、像平面坐标系O'-x'y'和像平面像素坐标系O₁-uv。

	Figure Option View Download New Window
	图1 四种坐标系Fig.1 Four kinds of coordinate systems

这4个步骤分别为:

(1)物方坐标系下P(X_W, Y_W, Z_W)变换到相机坐标系下P(x, y, z), 其过程可表示为:

$\begin{matrix} [\begin{matrix} x \\ y \\ z \end{matrix}] = R [\begin{matrix} X_{W} \\ Y_{W} \\ Z_{W} \end{matrix}] + t = [\begin{matrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33} \end{matrix}] [\begin{matrix} X_{W} \\ Y_{W} \\ Z_{W} \end{matrix}] + [\begin{matrix} t_{1} \\ t_{2} \\ t_{3} \end{matrix}] \end{matrix}$ (1)

式中:R为一个3× 3旋转矩阵; t为一个3× 1平移向量; r_ij(i, j=1, 2, 3)为旋转矩阵参数, 是关于相机姿态参数中旋转角(φ , ω , κ )的函数; t_i为反映相机姿态的平移参数。

(2)相机坐标系下P(x, y, z)基于针孔模型规范化投影得到归一化坐标p'(x', y'), 其过程可表示为:

$\begin{matrix} [\begin{matrix} x' \\ y' \end{matrix}] = [\begin{matrix} x / z \\ y / z \end{matrix}] \end{matrix}$ （2）

(3)归一化坐标p'(x', y')引入畸变校正后的结果为p″(x″, y″), 其过程可表示为:

$\begin{matrix} [\begin{matrix} x″ \\ y″ \end{matrix}] = (1 + k_{1} r^{2} + k_{2} r^{4}) [\begin{matrix} x' \\ y' \end{matrix}] + [\begin{matrix} 2 p_{1} x'y' + p_{2} (r^{2} + 2 x'^{2}) \\ p_{1} (r^{2} + 2 y'^{2}) + 2 p_{2} x'y' \end{matrix}] \end{matrix}$ (3)

式中:k₁、k₂均为径向畸变系数; p₁、p₂均为切向畸变系数; r²=x'²+y'²。

(4)畸变改正后的p″(x″, y″)变换到像平面像素坐标系下p(u, v), 其过程可表示为:

$\begin{matrix} [\begin{matrix} u \\ v \end{matrix}] = [\begin{matrix} x ″ f_{x} / d_{x} + c_{x} \\ y ″ f_{y} / d_{y} + c_{y} \end{matrix}] \end{matrix}$ (4)

式中:f_x、f_y分别为相机在x、y方向的主距; (c_x, c_y)为像主点O'(摄影光轴与像平面交点)的坐标, 即O'在像平面像素坐标系O₁-uv下的坐标; d_x、d_y分别为单位像素在x、y方向的物理尺寸(mm/pixel), 可根据传感器尺寸和分辨率计算, 视为已知。

综合步骤(1)(2)(4), 得到如下等价表达式:

$\begin{matrix} s \cdot p_{0} = A (R |t) \cdot P_{0} \end{matrix}$ (5)

式中:s为比例因子; p₀=(u, v, 1)^T为图像像素点的齐次坐标; P₀=(X, Y, Z, 1)为空间点的齐次坐标; A为相机内参数矩阵; (R|t)为外参数矩阵。

式(5)表达了图像点p和空间点P间的映射关系, 进一步展开得到式(6):

$\begin{matrix} s {[\begin{matrix} u & v & 1 \end{matrix}]}^{T} = [\begin{matrix} f_{x} / d_{x} & 0 & c_{x}^{} \\ 0 & f_{y} / d_{y} & c_{y} \\ 0 & 0 & 1 \end{matrix}] \cdot [\begin{matrix} r_{11} & r_{12} & r_{13} & t_{1} \\ r_{21} & r_{22} & r_{23} & t_{2} \\ r_{31} & r_{32} & r_{33} & t_{3} \end{matrix}] [\begin{matrix} X_{W} \\ Y_{W} \\ Z_{W} \\ 1 \end{matrix}] \end{matrix}$ （6）

1.2 相机标定参数

式(6)表达了图像点p和空间点P之间的映射关系, 在顾及镜头畸变引起的像点坐标改正(式(3))后, 认为把物方坐标与像平面的像素坐标联系起来的参数共有3类:①相机的内参数(c_x, c_y, f_x, f_y); ②相机的外参数(t₁, t₂, t₃, φ , ω , κ ); ③相机镜头畸变系数(k₁, k₂, p₁, p₂)。相机的外参数是指摄影时相机的姿态参数, 外参数随摄影时相机位置及姿态的变化而变化; 内参数是指像主点坐标和相机的主距, 它们与畸变系数一样, 相对稳定。因此, 相机标定参数是指相机的内参数(c_x, c_y, f_x, f_y)和畸变系数(k₁, k₂, p₁, p₂)。非量测相机的标定就是确定这些标定参数的过程。

2 数学模型

根据引入透镜径向和切向畸变的针孔模型, 通过相机标定参数(c_x, c_y, f_x, f_y, k₁, k₂, p₁, p₂)和摄影时相机姿态参数(t₁, t₂, t₃, φ , ω , κ ), 建立空间点P与其投影到像平面上像点p之间的联系, 如式(7)所示:

$\begin{matrix} \{\begin{matrix} u = f_{x} [x' (1 + k_{1} r^{2} + k_{2} r^{4}) + 2 p_{1} x' y' + \\ p_{2} (r^{2} + 2 x'^{2})] / d_{x} + c_{x} \\ v = f_{y} [y' (1 + k_{1} r^{2} + k_{2} r^{4}) + p_{1} (r^{2} + 2 y'^{2}) + \\ 2 p_{2} x' y'] / d_{y} + c_{y} \end{matrix} \end{matrix}$ （7）

式中:x'、y'由式(8)计算; r²=x'²+y'²。

$\begin{matrix} \{\begin{matrix} x' = (r_{11} X + r_{12} Y + r_{13} Z + t_{1} \frac{)}{(} r_{31} X + \\ r_{32} Y + r_{33} Z + t_{3}) \\ y' = (r_{21} X + r_{22} Y + r_{23} Z + t_{2} \frac{)}{(} r_{31} X + \\ r_{32} Y + r_{33} Z + t_{3}) \end{matrix} \end{matrix}$ （8）

基于式(7)(8), 引入测量间接平差理论, 建立像点坐标观测值的误差方程式为:

$\begin{matrix} \begin{matrix} (\begin{matrix} v_{u_{ij}} \\ v_{v_{ij}} \end{matrix}) = (\begin{matrix} \frac{\partial u_{ij}}{\partial f_{x}} & \frac{\partial u_{ij}}{\partial f_{y}} & \frac{\partial u_{ij}}{\partial c_{x}} & \frac{\partial u_{ij}}{\partial c_{y}} \\ \frac{\partial v_{ij}}{\partial f_{x}} & \frac{\partial v_{ij}}{\partial f_{y}} & \frac{\partial v_{ij}}{\partial c_{x}} & \frac{\partial v_{ij}}{\partial c_{y}} \end{matrix}) (\begin{matrix} d f_{x} \\ d f_{y} \\ d c_{x} \\ d c_{y} \end{matrix}) + \\ (\begin{matrix} \frac{\partial u_{ij}}{\partial k_{1}} & \frac{\partial u_{ij}}{\partial k_{2}} & \frac{\partial u_{ij}}{\partial p_{1}} & \frac{\partial u_{ij}}{\partial p_{2}} \\ \frac{\partial v_{ij}}{\partial k_{1}} & \frac{\partial v_{ij}}{\partial k_{2}} & \frac{\partial v_{ij}}{\partial p_{1}} & \frac{\partial v_{ij}}{\partial p_{2}} \end{matrix}) (\begin{matrix} d k_{1} \\ d k_{2} \\ d p_{1} \\ d p_{2} \end{matrix}) + \\ (\begin{matrix} \frac{\partial u_{ij}}{\partial φ_{j}} & \frac{\partial u_{ij}}{\partial ω_{j}} & \frac{\partial u_{ij}}{\partial κ_{j}} & \frac{\partial u_{ij}}{\partial t_{1 j}} & \frac{\partial u_{ij}}{\partial t_{2 j}} & \frac{\partial u_{ij}}{\partial t_{3 j}} \\ \frac{\partial v_{ij}}{\partial φ_{j}} & \frac{\partial v_{ij}}{\partial ω_{j}} & \frac{\partial v_{ij}}{\partial κ_{j}} & \frac{\partial v_{ij}}{\partial t_{1 j}} & \frac{\partial v_{ij}}{\partial t_{2 j}} & \frac{\partial v_{ij}}{\partial t_{3 j}} \end{matrix}) (\begin{matrix} d φ_{j} \\ d ω_{j} \\ d κ_{j} \\ d t_{1 j} \\ d t_{2 j} \\ d t_{3 j} \end{matrix}) - \\ (\begin{matrix} u_{ij} - u_{ij}^{0} \\ v_{ij} - v_{ij}^{0} \end{matrix}) \end{matrix} \end{matrix}$ （9）

式中:u_ij、v_ij为第j张像片的第i个像点坐标的观测值; $\begin{matrix} {u_{ij}}^{0} \end{matrix}$ 、 $\begin{matrix} {v_{ij}}^{0} \end{matrix}$ 为第j张像片的第i个像点坐标的近似值; v_uij、v_vij分别为u_ij和v_ij的改正数; df_x、df_y、dc_x、dc_y、dk₁、dk₂、dp₁和dp₂为标定参数近似值的改正数, 是待求未知数; dφ _j、dω _j、dκ _j、dt₁_j、dt₂_j、dt₃_j为拍摄第j张像片时相机的姿态参数(外参数)改正数, 也是待求未知数; ∂u_ij/∂f_x, …, ∂u_ij/∂t₃_j, ∂v_ij/∂f_x, …, ∂v_ij/∂t₃_j构成了待求未知数的系数矩阵元素。

式(9)写成简化矩阵形式为:

$\begin{matrix} V = BX - L (10) \end{matrix}$

最小二乘解为:

$\begin{matrix} X = (B^{T} {B)}^{- 1} B^{T} L (11) \end{matrix}$

单位权中误差为:

$\begin{matrix} σ_{0} = \pm \sqrt[]{[V^{T} V] / (n - t)} (12) \end{matrix}$

式中:n为误差方程数量; t为待求未知数的数量。标定参数的中误差为:

$\begin{matrix} σ_{X} = σ_{0} \sqrt[]{Q_{X}} = σ_{0} \sqrt[]{(B^{T} {B)}^{- 1}} (13) \end{matrix}$

式(9)~(13)即是把测量平差理论与计算机视觉相结合建立的相机标定参数解算及精度评定的数学模型。

3 相机标定软件的设计及实现

以式(9)~(13)建立的相机标定数学模型为基础, 结合相机标定的方便快捷、灵活性要求及标定软件的易编制性和易操作性要求, 以液晶显示屏棋盘格网作为标定参照物, 以Microsoft Visual Studio为开发平台, 利用MFC结合OpenCV编制了相机标定软件Camera Calibration 1.0。

3.1 软件总体功能及实现流程

软件总体功能如下:①新建工程及生成不同规格的计算机屏幕棋盘格网; ②采用5摄站法从不同角度拍摄棋盘格网像片并导入工程; ③提取各像片上格网点的亚像素级坐标; ④计算相机的内参数、外参数及畸变系数; ⑤误差分析及重投影误差散点图的绘制; ⑥评定精度及生成相机标定报告; ⑦校正影像。图2为系统实现流程。

	Figure Option View Download New Window
	图2 系统实现流程Fig.2 Workflow of system implementation

3.2 编程实现方法

以Microsoft Visual Studio为平台, 采用MFC, 结合OpenCV, 基于计算机视觉和测量平差理论的相机标定数学模型, 编制相机标定与影像校正软件。编程中用到了OpenCV的cvCalibrateCmera2()、cvProjectPoints2()、cvUndistort2()等函数, 其余计算皆采用VC++自主开发完成。

3.3 误差分析及精度评定

(1)根据式(12)(13)进行单位权中误差及标定参数中误差的计算, 获取标定参数精度。

(2)像点的重投影误差计算及图形绘制。根据相机标定的内、外参数, 结合格网点的已知物方三维坐标(X, Y, Z), 运用cvProjectPoints获取格网点投影到像平面的坐标(x', y'), 再与像片格网点的提取坐标(x, y)比较得到误差, 并绘制重投影误差散点图来直观分析误差分布状况。在散点图上可追踪误差超限点, 重新提取其坐标并重新计算标定参数。

(3)格网点物方三维坐标的反演误差分析。根据相机标定的内、外参数, 结合像片格网点的提取坐标(x, y), 运用测量间接平差理论, 解算格网点的物方三维坐标(X', Y', Z'), 与其已知坐标(X, Y, Z)比较, 得到格网点X、Y、Z方向及点位中误差, 评定格网点三维坐标反演精度。

4 相机标定试验

4.1 Canon 5D Marx II 28mm定焦镜头的标定试验

(1)试验环境

试验装置包括:计算机、待标定的Canon EOS 5D Marx II数码相机、28 mm定焦镜头。

采用5摄站旋转法定焦拍摄25张棋盘格网影像(见图3), 采集影像的分辨率为5616× 3744。

	Figure Option View Download New Window
	图3 拍摄的25张标定影像Fig.3 Twenty-five images photographed for calibration

(2)试验结果及精度

将标定影像导入系统中, 经过格网点坐标提取、标定计算、误差反分析及精度评定等环节, 得到相机标定参数及其精度如表1所示。

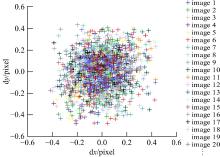
根据表1, 结合Canon 5D Marx II像素大小(像素宽度为0.0064 mm, 像素高度为0.0064 mm), 可知标定参数精度在± 1 pixel内。把表1中求出的标定参数与格网点的物方坐标相结合, 进行像点坐标的重投影并绘制误差散点图(见图4), 图4表明像点坐标的重投影误差也在± 1 pixel内。同理, 把求出的标定参数与格网点的像点坐标相结合, 反演格网点的物方坐标并与格网点的已知坐标进行对比, 计算得到格网点物方坐标反演的实际精度为m=± 0.2 pixel。

表1 Canon 5D Marx II(28 mm定焦镜头)标定参数及其精度 Table 1 Calibration parameter and its precision of Canon 5D Marx II with prime lens 28 mm

	Figure Option View Download New Window
	图4 重投影误差散点图Fig.4 Scatter diagram of reprojection errors

4.2 与同类软件对比试验

(1)试验环境

试验装置包括:计算机; 武汉朗视软件公司基于张祖勋院士提出的多基线摄影测量原理而研发的数字近景摄影测量系统Lensphoto; 本文设计的标定软件Camera Calibration 1.0; 待标定的数码相机Canon EOS 5D Marx II; 28 mm定焦镜头。采集影像的分辨率为5616× 3744。

(2)试验结果分析

使用同一相机在相同的5个测站及拍摄角度, 分别对同一固定位置的标定参照物(本系统使用LCD棋盘格网, Lensphoto使用LCD规则散点)进行拍摄, 经各自标定软件处理得出的标定结果如表2所示。

表2 Camera Calibration 1.0与Lensphoto标定结果对比 Table 2 Contrast of calibration results of Camera Calibration 1.0 and Lensphoto

从表2可以看出, 两个系统标定结果中, 焦距和主点只是在微米级出现差异, 畸变系数的数量级及符号均一致, 进一步验证了本文基于计算机视觉和测量平差理论的相机标定模型的正确性以及研发的相机标定软件Camera Calibration 1.0的可靠性。

5 工程应用

5.1 工程背景

以长春市净月潭杨家沟采石场边坡(见图5)的工程地质条件调查为例, 应用数字近景摄影测量技术, 以非量测相机为传感器摄取边坡影像, 结合边坡控制测量成果, 建立边坡三维模型, 解译边坡岩体大量随机结构面迹线、产状信息, 为边坡稳定性评价提供详实、准确、可靠的基础数据^{[20, 21]}。

	Figure Option View Download New Window
	图5 杨家沟采石场远景图Fig.5 Distant view of Yangjiagou quarry

5.2 非量测相机的标定

采用Canon 50D普通数码相机(像素宽度为0.00469 mm, 像素高度为0.00470 mm)对杨家沟采石场边坡进行了影像的获取, 共拍摄了7个像对。采用Camera Calibration 1.0进行相机标定, 标定结果及精度如表3所示。

5.3 边坡影像的获取及校正

采用近似正直摄影方式, 共拍摄7个像对, 结合表3中的相机标定结果, 采用Camera Calibration 1.0进行了边坡影像的畸变校正。

表3 拍摄杨家沟采石场边坡的Canon 50D相机标定结果 Table 3 Calibration results of Canon 50D used for slope photography in Yangjiagou quarry

5.4 边坡三维建模及结构面信息获取

把校正后的边坡影像与野外控制测量成果相结合, 采用数字摄影测量工作站VirtuoZo进行边坡三维建模。经检查, 模型点位测量精度在± 3 cm内, 确立边坡三维模型, 在模型上对结构面进行判识、量测及参数解算, 共提取1561条结构面的迹长和产状信息, 如表4所示, 其中α 为倾角, β 为倾向。

表4 基于数字近景摄影测量获取的结构面信息 Table 4 Acquired discontinuity information of slope based on digital close range photogrammetry

5.5 产状信息的验证

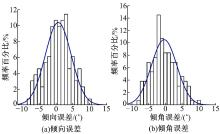
通过与边坡下部罗盘测得的结构面产状信息和边坡上部人员难以到达的免棱镜全站仪产状测量信息进行对比, 验证产状信息。统计了131条结构面, 对比得到的产状误差分布直方图及拟合曲线如图6所示。

	Figure Option View Download New Window
	图6 产状误差分布直方图及拟合曲线Fig.6 Error distribution histogram and its fitting curve of orientations

从图6可以看出, 倾向和倾角的误差均符合偶然误差特性, 采用测量误差理论的中误差计算式^[20]得到基于非量测相机拍摄边坡影像获得的产状精度在± 4° 内, 与罗盘产状测量的精度基本相当。可以获取边坡岩体大量随机结构面的信息, 为边坡稳定性评价提供可靠的基础数据。也间接验证了非量测相机标定参数的可靠性及其在岩土工程勘察中的实用性。

6 结论

(1)建立了基于计算机视觉和测量平差理论的数码相机标定模型, 该模型准确、可靠, 不仅能计算像点坐标的重投影误差, 而且能计算物方空间的三维坐标反演误差, 尤其能评定出标定参数的精度, 克服了传统计算机视觉中只计算像点坐标重投影误差的单一精度评定方法的局限。

(2)开发了相机标定和影像校正系统Camera Calibration 1.0。以计算机屏幕棋盘格网为标定参照物, 以Microsoft Visual Studio为开发平台, 利用MFC结合OpenCV进行相机标定软件的编制。该软件具有操作便捷、适用性强、占用内存少、运行效率高的特点。对于棋盘格网点提取, 可以自动化批处理, 也可以人工添加、编辑, 适应性更强, 克服了以往相机标定软件中因角点提取失败不能求解而对标定像片拍摄的高要求。不仅实现了相机的快速、高精度标定, 而且能进行影像的畸变校正, 可以满足岩土工程勘察中岩质边坡结构面信息获取的需要。

(3)该系统的相机标定参数精度在± 1 pixel内, 能够达到国内外同类软件的技术水平。

(4)随着工程领域非接触测量需求的增加和相机标定技术的成熟, 非量测相机将发挥越来越重要的作用。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	林冬梅, 张爱华, 沈蓉, 等. 双目视觉脉搏测量系统中的相机同步采集方法[J]. 吉林大学学报: 工学版, 2015, 45(6): 1999-2006. Lin Dong-mei, Zhang Ai-hua, Shen Rong, et al. Dual-camera synchronous acquisition method for binocular vision pulse measurement system[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(6): 1999-2006. [本文引用:1]
[2]	杨立云, 杨仁树, 赵雪楠, 等. 几种典型变质岩的冲击断裂焦散线实验探讨[J]. 岩石力学与工程学报, 2015, 34(4): 1-8. Yang Li-yun, Yang Ren-shu, Zhao Xue-nan, et al. Experimental investigation on dynamic fracture of some metamorphic rock using reflected caustics[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(4): 1-8. [本文引用:1]
[3]	魏巍, 李智慧, 赵永华, 等. 基于智能相机的混合交通流检测方法[J]. 吉林大学学报: 工学版, 2013, 43(4): 866-870. Wei Wei, Li Zhi-hui, Zhao Yong-hua, et al. Developing a smart camera for mixed traffic flow detection[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 866-870. [本文引用:1]
[4]	韩成, 秦贵和, 宫宇, 等. 基于彩色结构光的三维重建方法[J]. 吉林大学学报: 工学版, 2013, 43(5): 1343-1351. Han Cheng, Qin Gui-he, Gong Yu, et al. Method for three-dimensional reconstruction based on color structured light[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(5): 1343-1351. [本文引用:1]
[5]	冯文灏. 近景摄影测量[M]. 武汉: 武汉大学出版社, 2002. [本文引用:1]
[6]	邱茂林, 马颂德, 李毅. 计算机视觉中摄像机定标综述[J]. 自动化学报, 2000, 26(1): 43-55. Qiu Mao-lin, Ma Song-de, Li Yi. Computer vision camera calibration summary[J]. Automatica Sinica, 2000, 26(1): 43-55. [本文引用:1]
[7]	Zhang Zheng-you. A flexible new technique for camera calibration[DB/OL]. [2016-02-01]. http://www.ece.northwestern.edu/~yingwu/teaching/EECS432/Reading/Zhang_TR98.pdf. [本文引用:1]
[8]	Tsai R Y. An efficient and accurate camera calibration technique for 3D machine vision[C]//IEEE Conference on Computer Vision and Pattern Recognition, Miami Beach, USA, 1986: 364-374. [本文引用:1]
[9]	Tsai R Y. A versatile camera calibration technique for high accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses[J]. IEEE Journal of Robotics and Automation, 1987, 3(4): 323-344. [本文引用:1]
[10]	张永军, 张祖勋, 张剑清. 利用二维DLT及光束法平差进行数字相机标定[J]. 武汉大学学报: 信息科学版, 2002, 27(6): 566-571. Zhang Yong-jun, Zhang Zu-xun, Zhang Jian-qing. Camera calibration using 2D DLT and bundle adjustment with planar scenes[J]. Geomatics and Information Science of Wuhan University, 2002, 27(6): 566-571. [本文引用:1]
[11]	詹总谦, 张祖勋, 张剑清. 基于LCD的相机标定精度及其误差分析[J]. 武汉大学学报: 信息科学版, 2008, 33(11): 1142-1145. Zhan Zong-qian, Zhang Zu-xun, Zhang Jian-qing. Precision and error analysis of LCD-based camera calibration method[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1142-1145. [本文引用:1]
[12]	詹总谦, 张祖勋, 张剑清. 基于稀疏矩阵技术的光束法平差快速算法设计[J]. 测绘通报, 2006(12): 5-8. Zhan Zong-qian, Zhang Zu-xun, Zhang Jian-qing. A fast algorithm of bundle adjustment based on sparse matrix technology[J]. Bulletin of Surveying and Mapping, 2006(12): 5-8. [本文引用:1]
[13]	张烁, 燕丹晨, 甄莹, 等. 利用线性变换和后方交会的月球车相机标定[J]. 测绘科学, 2015, 40(11): 29-33. Zhang Shuo, Yan Dan-chen, Zhen Ying, et al. Calibration of lunar rover's stereo-camera based 3D DLT and multi-image resection[J]. Science of Surveying and Mapping, 2015, 40(11): 29-33. [本文引用:1]
[14]	崔红霞, 孙杰, 林宗坚, 等. 非量测数码相机的畸变差检测研究[J]. 测绘科学, 2005, 30(1): 105-107, 112. Cui Hong-xia, Sun Jie, Lin Zong-jian, et al. The research on distortion calibration of the non-measurement camera[J]. Science of Surveying and Mapping, 2005, 30(1): 105-107, 112. [本文引用:1]
[15]	谭华春, 夏红卫, 李琴, 等. 车载摄像机的立体标定方法[J]. 吉林大学学报: 工学版, 2013, 43(增刊1): 352-356. Tan Hua-chun, Xia Hong-wei, Li Qin, et al. Three-dimensional calibration for on-board camera[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(Sup. 1): 352-356. [本文引用:1]
[16]	谢文寒. 基于多像灭点进行相机标定的方法研究[D]. 武汉: 武汉大学遥感信息工程学院, 2004. Xie Wen-han. Camera calibration based on vanishing points of multi-image[D]. Wuhan: School of Remote Sensing and Information Engineering, Wuhan University, 2004. [本文引用:1]
[17]	赵亚凤, 胡峻峰. 一种双正交消隐点的双目相机标定方法[J]. 液晶与显示, 2016, 31(10): 958-966. Zhao Ya-feng, Hu Jun-feng. Binocular self calibration using two pairs of orthogonal vanishing points[J]. Chinese Journal of Liquid Crystal and Displays, 2016, 31(10): 958-966. [本文引用:1]
[18]	武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2011. [本文引用:1]
[19]	吉林大学. 数码相机标定及影像校正系统Camera Calibration 1. 0[P]. 中国: 2012SR039060. [本文引用:1]
[20]	王凤艳, 陈剑平, 杨国东, 等. 基于数字近景摄影测量的岩体结构面几何信息解算模型[J]. 吉林大学学报: 地球科学版, 2012, 42(6): 1839-1846. Wang Feng-yan, Chen Jian-ping, Yang Guo-dong, et al. Solution models of geometrical information of rock mass discontinuities based on digital close range photogrammetry[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(6): 1839-1846. [本文引用:2]
[21]	王凤艳, 黄润秋, 陈剑平, 等. 基于免棱镜全站仪的岩体边坡控制测量及结构面产状检验测量[J]. 吉林大学学报: 工学版, 2013, 43(6): 1607-1614. Wang Feng-yan, Huang Run-qiu, Chen Jian-ping, et al. Control surveying of rock mass slope and orientation validation measurement of discontinuities based on reflectorless total station instrument[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(6): 1607-1614. [本文引用:1]

2015

0.0

. 2015, 45(6):1999-2006

Dual-camera synchronous acquisition method for binocular vision pulse measurement system

双目视觉脉搏测量系统中的相机同步采集方法

Lin Dong-mei , Zhang Ai-hua , Shen Rong

林冬梅, 张爱华, 沈蓉

... 0 引言普通数码相机(非量测相机)的普及及其标定技术的日益成熟,使其在很多领域发挥量测作用^[1,2,3,4] ...

2015

0.0

. 2015, 34(4):1-8

Experimental investigation on dynamic fracture of some metamorphic rock using reflected caustics

几种典型变质岩的冲击断裂焦散线实验探讨

Yang Li-yun , Yang Ren-shu , Zhao Xue-nan

杨立云, 杨仁树, 赵雪楠

... 0 引言普通数码相机(非量测相机)的普及及其标定技术的日益成熟,使其在很多领域发挥量测作用^[1,2,3,4] ...

2013

0.0

. 2013, 43(4):866-870 DOI:doi:10.7964/jdxbgxb201304004

Developing a smart camera for mixed traffic flow detection

基于智能相机的混合交通流检测方法

Wei Wei , Li Zhi-hui , Zhao Yong-hua

魏巍, 李智慧, 赵永华

摘　要：针对目前缺乏混合交通视频智能检测设备的问题,利用CCD传感器与DSP芯片构建了智能相机框架体系和硬件原型系统,采用背景初始化、背景模型与前景获取、物体分割、特征提取、多目标识别分类、摄像机参数标定等视频图像处理技术,构建了混合交通流检测软件方法体系,开发了相应的嵌入式算法系统,实现了混合交通流参数检测。在不同交通状态下的测试结果反映了该系统具有良好的性能,可实现混合交通流参数检测。本方法可为混合交通流智能相机的研发提供借鉴和参考。

... 0 引言普通数码相机(非量测相机)的普及及其标定技术的日益成熟,使其在很多领域发挥量测作用^[1,2,3,4] ...

2013

0.0

. 2013, 43(5):1343-1351 DOI:10.7964/jdxbgxb201305032

Method for three-dimensional reconstruction based on color structured light

基于彩色结构光的三维重建方法

Han Cheng , Qin Gui-he , Gong Yu

韩成, 秦贵和, 宫宇

1. College of Computer Science and Technology, Jilin University, Changchun 130012, China; 2. School of Computer Science and Technology, Changchun University of Science and Technology, Changchun 130022, China; 3. Department of Foreign Language, Jilin Vocational and Technical College of Traffic, Changchun 130021, China

In this study, first, by executing the distortion correction and calibration on the camera and projector, the corresponding homography transformation matrix is determined. Then, in order to quickly obtain high precision code values from color encoded structured light under complex projection conditions, a color structured light coding method based on topology structure and local structured model is proposed. Finally, the methods for extracting encoded feature points based on waveform analysis and for classifying colors based on clustering analysis are developed. In addition, the characteristics of the encoded images are also exploited to improve the decoding accuracy. According to the homography transform matrix and the matching relationship of the code values of the feature points in the encoded images before and after modulation, the three-dimensional information of the feature points is calculated. Experimental results show that the decoding accuracy is higher than 99.5%. Because that the positions of the projector and camera are not strictly constrained, the method is applicable for building a reconstruction system that can rapidly and accurately generate point clouds from three-dimensional objects.

通过对摄像机和投影机进行畸变校正和标定,确定了相应单应性变换矩阵。为了在复杂投影条件下对彩色结构光编码图像进行快速高精度解码,提出了基于拓扑结构和局部结构化的单幅彩色结构光编码方法以及基于波形分析的编码特征点提取方法和基于聚类分析的颜色分类方法,并利用编码图像本身特性提高解码精度和正确率。根据单应性变换矩阵和编码图像中每个特征点编码值调制前后的匹配关系,计算特征点的三维信息。实验结果表明,特征点的解码正确率超过99.5%。由于对投影机和摄像机的位置没有严格的限定,该方法适合快速搭建三维物体重构系统以及快速高精度地获得物体的点云。

... 0 引言普通数码相机(非量测相机)的普及及其标定技术的日益成熟,使其在很多领域发挥量测作用^[1,2,3,4] ...

2002

0.0

... )和比例尺不一致性(ds)等的一个过程^[5] ...

2000

0.0

. 2000, 26(1):43-55

Computer vision camera calibration summary

计算机视觉中摄像机定标综述

Qiu Mao-lin , Ma Song-de , Li Yi.

邱茂林, 马颂德, 李毅

In this paper the camera calibration methods in photogrammertry and computervision are reviewed, categorized and compared with. Features of the applicationof camera calibration methods in computer vision are discussed.

回顾了摄影测量学和计算机视觉中的各种摄像机定标方法,对各种方法进行了分析、比较、并讨论了摄像机定标方法应用于计算机视觉中的特点.

... 相机标定的典型方法有计算机视觉方法和摄影测量方法^[6] ...

0.0

... 计算机视觉中,有Zhang的平面格网法^[7]和Tsai的两步法^[8,9] ...

1986

0.0

... 计算机视觉中,有Zhang的平面格网法^[7]和Tsai的两步法^[8,9] ...

1987

0.0

... 计算机视觉中,有Zhang的平面格网法^[7]和Tsai的两步法^[8,9] ...

2002

0.0

. 2002, 27(6):566-571

Camera calibration using 2D DLT and bundle adjustment with planar scenes

利用二维DLT及光束法平差进行数字相机标定

Zhang Yong-jun , Zhang Zu-xun , Zhang Jian-qing.

张永军, 张祖勋, 张剑清

... 摄影测量方法有基于二维直接线性变换(2D-DLT)^[10]、基于三维直接线性变换(3D-DLT)和共线方程的光束法平差^[11,12,13] ...

2008

0.0

. 2008, 33(11):1142-1145

Precision and error analysis of LCD-based camera calibration method

基于LCD的相机标定精度及其误差分析

Zhan Zong-qian , Zhang Zu-xun , Zhang Jian-qing.

詹总谦, 张祖勋, 张剑清

... 摄影测量方法有基于二维直接线性变换(2D-DLT)^[10]、基于三维直接线性变换(3D-DLT)和共线方程的光束法平差^[11,12,13] ...

0.0

. , 2006(12):5-8 DOI:doi:10.3969/j.issn.0494-0911.2006.12.002

A fast algorithm of bundle adjustment based on sparse matrix technology

基于稀疏矩阵技术的光束法平差快速算法设计

Zhan Zong-qian , Zhang Zu-xun , Zhang Jian-qing.

詹总谦, 张祖勋, 张剑清

首先给出光束法平差法方程式及其改化形式的一般化公式,并说明各系数矩阵的实际意义,从而可以方便地借助稀疏矩阵技术直接组建并存储各系数矩阵.其次,详细介绍如何设计一种可行的、高效的,集一般的光束法区域网平差、多片空间后方交会、多片前方交会和自由网平差于一体的快速平差算法.最后通过多组数据说明算法的可行性和高效性.

... 摄影测量方法有基于二维直接线性变换(2D-DLT)^[10]、基于三维直接线性变换(3D-DLT)和共线方程的光束法平差^[11,12,13] ...

2015

0.0

. 2015, 40(11):29-33

Calibration of lunar rover's stereo-camera based 3D DLT and multi-image resection

利用线性变换和后方交会的月球车相机标定

Zhang Shuo , Yan Dan-chen , Zhen Ying

张烁, 燕丹晨, 甄莹

... 摄影测量方法有基于二维直接线性变换(2D-DLT)^[10]、基于三维直接线性变换(3D-DLT)和共线方程的光束法平差^[11,12,13] ...

2005

0.0

. 2005, 30(1):105-107,112

The research on distortion calibration of the non-measurement camera

非量测数码相机的畸变差检测研究

Cui Hong-xia , Sun Jie , Lin Zong-jian

崔红霞, 孙杰, 林宗坚

... 从相机标定采用的人造参照物上,分为室外控制场、室内控制场、简易三维刚体、平面格网、一维物体等^{[14,15,16,17]} ...

2013

0.0

. 2013, 43(增刊1):352-356

Three-dimensional calibration for on-board camera

车载摄像机的立体标定方法

Tan Hua-chun , Xia Hong-wei , Li Qin

谭华春, 夏红卫, 李琴

摘　要：提出了一种简便实用的基于立体标定板的车载摄像机标定方法。基于自制立体标定板对车载摄像机进行标定,方法比较便捷,精度较高,且方便车载摄像机进行后续检测等工作。实验结果及误差分析验证了该方法的可行性。

... 从相机标定采用的人造参照物上,分为室外控制场、室内控制场、简易三维刚体、平面格网、一维物体等^{[14,15,16,17]} ...

2004

0.0

. 2004, :-

Camera calibration based on vanishing points of multi-image[D]. Wuhan:School of Remote Sensing and Information Engineering,

基于多像灭点进行相机标定的方法研究[D]

Xie Wen-han.

谢文寒

人类从外界环境获取的信息中,80%来自于视觉。人的眼睛将获取的信息传入大脑,由大脑根据知识和经验,对信息进行处理与识别。随着数字技术的出现与发展,计算机视觉替代了人眼与大脑,实现了对周围环境进行简单识别与理解的功能。计算机视觉的研究目标是使计算机具有通过二维图像认知三维环境信息的能力,这种能力将不仅使机器感知三维环境中物体的几何信息,包括它的形状、位置、姿态、运动等,而且能对它们进行描述、存储,识别与理解。而若通过二维图像感知三维世界,传感器的定标(或标定)成为关键技术之一。近年来,随着数字化技术的不断进步,硬件装置价格的不断下降和计算机性能的不断提高,数码相机也得到了普及,许多计算机视觉系统也都以普通数码相机作为获取数据的主要传感器。因此,数码相机(摄像机)的标定逐渐成为计算机视觉领域以及摄影测量领域的研究热点之一。国内外的许多摄影测量及计算机视觉界的专家学者提出多种多样的标定方法。然而,没有哪一种标定方法可以用于所有应用,不同的用途、不同的环境就要采用不同的标定方法。本文以基于灭点的标定方法为切入点,首先阐述几种传统相机标定方法与自标定技术以及存在的问题,随后提出了几种既不需要控制场同时精度又较高的基于多像灭点的标定方法。这些标定方法操作简易、灵活,可做到“随时随地”标定相机,若将标定结果用于人工规则建筑物的三维重建,该方法还可进行在线标定。本文涉及的主要研究内容集中在四个方面:(1)直线检测与灭点的确定;(2)基于多像灭点的标定方法;(3)基于点线混合的相机标定方法;(4)基于多平面格网的相机标定方法。 1)直线检测与灭点的确定。灭点是空间平行线在影像上投影的交点。它作为本文所提出的标定方法的重要因素,贯穿文章始末。一般灭点位于影像边界以外,甚至是无穷远处,因此标定前确定灭点的最佳位置至关重要。灭点是直线的交点,本文研究了一种自适应的最小二乘直线模板匹配技术用于高精度的提取影像中的直线信息。由于影像中噪声的存在,使得平行线在影像上未必交于一点,因此,从摄影测量角度出发,研究了一种以影像直线为观测值,建立直线与灭点相关的平差模型确定灭点的方法。该方法既不需要将直线投影到球面坐标,也不需要对大量直线作统计特性分析,当存在大量多余直线观测时,这种平差方法可快速、准确地计算出灭点的最优位置。 2)基于多像灭点的相机标定。从单像灭点标定方法的误差分析入手,以灭点为桥梁,通过灭点的几何特性将影像中直线观测值与相机方位元素直接关联,并对多像联合建立平差模型,以解求未知的相机内外方位元素。同时,非线性畸变模型和几何约束条件也直接纳入到平差标定模型中,多种类型未知参数统一解求,使标定精度大大提高。 3)基于点线混合的相机标定。分析了长焦距相机因视场角小在应用灭点标定时遇到的问题,首次研究了专门针对长焦距、小视场角相机的基于点线混合的标定方法。该方法通过一种无位移、多方位的全景摄影方式扩展长焦距相机的视场角,并用基于点的自标定与基于线的平差模型相结合的方法建立统一模型对相机进行标定。 4)基于平面格网的相机标定。通过分析灭点与灭线的约束特性,利用两个灭点也可进行相机标定。对一个或(多个平行)平面格网或人工建筑物某一立面进行多位移、多角度拍摄,利用多像灭点约束建立标定模型,最后通过矩阵分解得到相机参数矩阵。该方法将三维方向的灭点信息发展到二维方向的灭点信息,且不需要任何物方控制点信息,使灭点标定方法得到进一步推广。

... 从相机标定采用的人造参照物上,分为室外控制场、室内控制场、简易三维刚体、平面格网、一维物体等^{[14,15,16,17]} ...

2016

0.0

... 从相机标定采用的人造参照物上,分为室外控制场、室内控制场、简易三维刚体、平面格网、一维物体等^{[14,15,16,17]} ...

2011

0.0

... 为此,本文从相机标定可靠性出发,在借鉴摄影测量方法的基础上,以计算机视觉中顾及畸变的针孔模型为基础,结合测量平差理论^[18],建立了基于计算机视觉和测量平差理论的相机标定数学模型,实现了标定参数的解算及其精度评定,克服了传统计算机视觉中只进行像点坐标重投影误差的单一精度评定方法的局限 ...

0.0

... 0^[19],并与近景摄影测量商业软件Lensphoto相机标定结果进行对比 ...

2012

0.0

. 2012, 42(6):1839-1846

Solution models of geometrical information of rock mass discontinuities based on digital close range photogrammetry

基于数字近景摄影测量的岩体结构面几何信息解算模型

Wang Feng-yan , Chen Jian-ping , Yang Guo-dong

王凤艳, 陈剑平, 杨国东

In order to obtain geometric information of rock mass discontinuities rapidly and comprehensively to improve stability evaluation quality, a series of solution models，3D trace model, 2D trace model of random projection plane and the orientation solution model with detailed criterion were put forward and established under the theories of spatial geometry, azimuth conception and projection transformation on the basis of obtaining spatial coordinates of discontinuities through digital close range photogrammetric technology. In the first place, more detailed information about trace distribution status could be displayed through 3D trace model, and in the second place, trace information of any important projection plane could be obtained through 2D trace model, therefore, its physical significance was highlighted. In addition, orientation obtaining precision based on orientation solution model was discussed through the theory of error. The experimental results demonstrated that the problem of orientation obtaining of approximate linear discontinuities could be solved when position measurement error was less than 2 cm on slope 3D model established by digital close range photogrammetry. On the whole, more abundant, detailed and comprehensive discontinuity information could be obtained and applied to the stability analysis and evaluation with the combination of digital close range photogrammetry and geometric information solution models of rock mass discontinuities.

为了快速、全面地获取岩体随机结构面信息而提高稳定性评价工作，在数字近景摄影测量测取结构面空间坐标的基础上，应用立体几何、方位概念和投影变换理论，提出并建立了基于空间坐标的结构面迹线三维模型、任一投影展示面的迹线二维模型和详细判据的产状解算模型。迹线三维模型数据更加详实展示迹线分布状况，迹线二维模型数据又能获得任一重要投影面的迹线信息并突显迹线物理意义；应用误差理论，探讨了基于数字近景摄影测量的产状解算模型获取产状的精度。实验表明，在数字近景摄影测量建立边坡三维模型点位测量精度≤2 cm时，能够解决近似线状结构面的产状获取问题。因此，岩体结构面几何信息解算模型与数字近景摄影测量相结合，可采集到更为全面的结构面几何信息并用于岩体稳定性评价。

... 1 工程背景以长春市净月潭杨家沟采石场边坡(见图5)的工程地质条件调查为例,应用数字近景摄影测量技术,以非量测相机为传感器摄取边坡影像,结合边坡控制测量成果,建立边坡三维模型,解译边坡岩体大量随机结构面迹线、产状信息,为边坡稳定性评价提供详实、准确、可靠的基础数据^[20,21] ...

... 从图6可以看出,倾向和倾角的误差均符合偶然误差特性,采用测量误差理论的中误差计算式^[20]得到基于非量测相机拍摄边坡影像获得的产状精度在#cod#x000b1 ...

2013

0.0

. 2013, 43(6):1607-1614

Control surveying of rock mass slope and orientation validation measurement of discontinuities based on reflectorless total station instrument

基于免棱镜全站仪的岩体边坡控制测量及结构面产状检验测量

Wang Feng-yan , Huang Run-qiu , Chen Jian-ping

王凤艳, 黄润秋, 陈剑平