在实际工程应用中, 结构损伤的大小直接关系到结构的使用安全, 因此应用红外热波无损检测技术对结构进行检测时, 不仅要求能够有效地检测到结构中存在的损伤, 还要能够识别出损伤的大小, 从而实现对结构寿命的预测和评估。为了实现基于热波图像的损伤定量识别, 首先要对增强处理后的热波图像进行损伤的分割提取。红外热波检测是一种基于热波理论的新型无损检测技术。该技术通过对被测对象施加周期、脉冲等函数形式的热激励, 使被测物体内部异性结构(缺陷或损伤, 如异物、异常结构等)以表面温度场变化的形式表现出来, 采用红外成像技术连续观测和记录被测物体表面的温度场变化, 从而获取物体的非均匀信息或表面下的结构异常^{[1, 2, 3]}。该技术具有检测面积大、检测效率高、单向、非接触以及能够直接测量出深度、厚度等优点, 在航空航天、汽车、建筑、石油化工、医学等领域得到了广泛的应用^[4]。但由于红外热像仪本身及外界环境的影响, 试验得到的红外热波序列图像普遍存在“ 低对比度、高背景及高噪声” 等问题, 为了提高热波技术的检测能力, 增强缺陷或损伤的显示度, 研究人员在改善图像质量、提高图像信噪比等方面做了大量的工作^[5]。

阈值法是基于区域实现图像分割的一种常用方法, 原理简单且易于实现^[6], 该方法根据选定的灰度阈值将图像分割成不同的区域。目前, 根据选定最佳阈值的准则不同, 阈值法可以分为多种^{[7, 8, 9]}, 其中最大类间方差(Otsu)法^[7]以图像中目标与背景之间类间方差的最大值作为分割准则, 对多类图像分割效果好且计算简单, 成为阈值分割较为常用的方法^{[10, 11, 12, 13, 14, 15]}。本文针对热波检测图像的特点, 将遗传算法(Genetic algorithm, GA)与Otsu法结合应用到热波图像的损伤分割提取中, 并将该方法的结果与基于直方图的人工阈值法分割结果进行了比较。

Otsu法是在最小二乘法的基础上推导演化而来的, 按照待处理图像的灰度分布特点, 将图像分割成目标及背景两个部分。在分割过程中若将目标错分为背景或将背景错分为目标都将使得图像中两部分的差别减小, 因此, 当利用类间方差最大时的阈值进行分割时, 图像中像素被错分的概率最小, 此阈值即是最佳的分割阈值。Otsu法获取最佳阈值的过程为:

设待分割图像I的灰度级有L个, 灰度值i的像素个数为n_i, 则图像中总的像素数为:

N=∑i=0L-1ni（1）

各灰度值出现的概率为:

pi=niN（2）

以分割阈值Th将图像分割为R₁和R₂两个区域, 则两个区域出现的概率分别为:

ω1=∑i=0Thni/N=∑i=0Thpi（3）

ω2=∑i=Th+1L-1ni/N=∑i=Th+1L-1pi=1-ω1（4）

以初始阈值分割后, 两个区域R₁和R₂的灰度均值分别为:

μ1=∑i=0Thni×i/∑i=0Thni=∑i=0Thpi×i/ω1（5）

μ2=∑i=Th+1L-1ni×i/∑i=Th+1L-1ni=∑i=Th+1L-1pi×i/ω2（6）

图像的整体灰度均值为:

μ=∑i=0L-1pi×i=ω1μ1+ω2μ2（7）

计算被阈值Th分割成的两个区域的类间方差d(Th)为:

d(Th)=ω1(μ1-μ)2+ω2(μ2-μ)2（8）

将式(7)代入式(8)中可得:

d(Th)=ω1ω2(μ1-μ2)2（9）

根据待处理图像的具体情况, 在0~L-1间改变分割阈值Th的大小, 求取最佳分割阈值Th_new, 使得图像按照该阈值分割为R₁和R₂两个区域后有d(Th_new)=max(d(Th)); 然后, 以Th_new为阈值去分割待处理图像即可得在该准则下的最佳分割结果。

Otsu法的核心在于计算图像被分割为两个区域后的类间方差, 但是在实际使用过程中, 待分割图像的灰度级越大, 得到最佳阈值的时间就越长, 图像分割效率就越低。为了解决Otsu法在图像分割中求解最佳阈值慢的问题, 本文将GA引入到最佳阈值的求解过程中, 以期达到全局最优、最快速求解的目的。

2.1 GA的基本原理

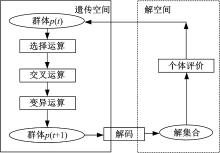
GA通过模拟自然界的进化过程求解问题的最优解, 具有鲁棒性强、适于并行处理等优点, 在图像处理、模式识别及工业优化控制中得到了广泛的应用。在使用GA进行问题的求解时, 为了获得最佳的适应度函数, 以选定的初值为初始点进行一定准则下的繁衍进化, 其过程一般包括参数编码、初始化种群、选定适应度函数、遗传操作的设计及控制参数的设定等, 遗传算法在求解实际问题中基本的寻优过程如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 基于GA的运算过程示意图Fig.1 Schematic diagram of operation process based on GA

2.2 基于GA-Otsu法的热波检测图像分割

Otsu法是在图像中像素灰度的取值范围内寻求最佳的分割阈值, 使分割后目标与背景之间的类间方差最大, 而GA能够非线性快速查找问题的最佳分割阈值Th_new及其最大方差, 因此将GA引入到传统的Otsu法之中, 利用GA的寻优能力求解热波图像的最佳分割阈值, 具体步骤为:

(1)对要寻优的解空间进行编码, 产生相应的染色体单元。

(2)初始化种群, 设定寻优过程的起始值。

(3)编码染色体单元, 设定类间方差作为染色体的评价函数。

(4)进行遗传操作:交叉及变异。

(5)繁衍。对新产生的种群重复上述操作, 随着种群的不断产生, GA在不断的繁衍中得到问题的最优解。

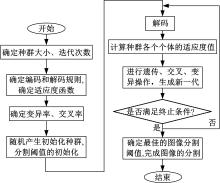
根据上述研究结果, 可得基于GA-Otsu法的热波检测图像分割流程, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 基于GA-Otsu法的热波检测图像分割流程Fig.2 Segmentation process of thermal waving inspection image based on GA-Otsu method

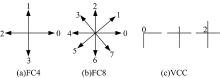
链码技术由Freeman^[16]于1961年提出, 基本思想是将图像中目标区域的边界采用一些首尾相连且具有特定长度和方向的直线段来表示。目前常用的链码技术有4邻域链码(FC4)、8邻域链码(FC8)及顶点链码(VCC)等, 其相关方法如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 三种链码表示方法Fig.3 Three kinds of chain code representation

由图3可知, FC4采用{i|i=0, 1, 2, 3}表示与水平方向逆时针成90° × i角度的4个方向; FC8采用{i|i=0, 1, …, 7}表示与水平方向逆时针成45° × i角度的8个方向; 而VCC采用{i|i=0, 1, 2}表示目标边界的曲线形状, 其中0表示目标区域的凸点, 1表示目标区域的延伸点, 2表示目标区域的凹点。综合考虑3种链码技术的优缺点及实现的难易程度, 本文采用FC8方法表示冲击边界, 并基于该方法实现对冲击损伤面积的定量识别。

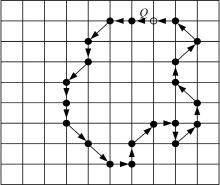
图4给出了采用FC8表示目标区域的一个例子, 将目标边界上的任意一点Q作为链码表示的起始点, 沿逆时针方向, 便可得到表示边界的一串链码值, 从而确定了目标区域的边界。图4中的FC8值为:Q→ 445656677021061232134。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 目标区域边界的FC8表示Fig.4 FC8 representation of target area boundary

由上述分析可知, 起始点Q的坐标及其链码值可以完整地表示图像中目标区域的位置和形状, 从而可以用边界内所有像素点的个数来表示目标区域的面积、周长等相关特征量, 而区域面积是描述区域大小的主要特征, 其定义为边界内所有像素点的数目。对于特定的目标区域R, 面积S_R可以表示为:

SR=∑(x, y)∈R1（10）

通过式(10)计算得到的面积为图像目标区域的像素值, 而对于热波图像中的损伤来说, 其实际面积大小可以通过实验过程中相应的尺寸标定转化获得。

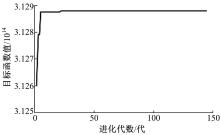
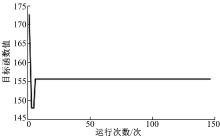
采用本文方法对增强后的热波图像进行分割, 相关参数设置为:染色体长度L=5; 种群大小N=20; 交叉概率p_c=0.7; 变异概率p_m=0.01; 终止进化代数T=150。通过寻优计算得到在最大类间方差准则下的最佳分割阈值Th=156, 所用时间为2.8210 s, 而传统Otsu法得到最佳分割阈值的时间为5.5324 s, 改进后的方法在一定程度上减少了阈值寻优所用的时间。利用该阈值对图像分割后的结果如图5所示。其最佳适应度值进化曲线和每一代的最佳阈值进化曲线分别如图6和图7所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 基于GA-Otsu法的热波检测图像分割结果Fig.5 Segmentation results of thermal waving inspection image based on GA-Otsu method

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 最佳适应度值进化曲线Fig.6 Optimal fitness value evolution curve

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 每一代的最佳阈值进化曲线Fig.7 Optimal threshold evolution curve for each generation

为了验证GA-Otsu法在热波检测图像分割中的有效性, 根据增强后图像的直方图采用人工阈值法对热波图像进行分割处理, 结果如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 基于人工阈值法的热波图像分割结果Fig.8 Segmentation results of thermal image based on artificial threshold method

从图8可以看出, 在基于阈值的图像分割中, 分割阈值是决定图像分割效果的关键因素, 不同的阈值获得了不同的分割效果。对于含有冲击损伤的热波图像来说, 采用基于图像直方图的人工阈值法虽然取得了一定的分割效果, 但是因为热波图像的直方图不是典型的双峰结构, 对于分割阈值的选取没有依据, 随意性较大; 当分割阈值Th=100时, 将图像中完好区域的地方因为表面处理不光滑或反光等引起的图像不均匀当成损伤区域而分割提取, 使得分割出来的损伤区域较大; 当分割阈值Th=200时, 虽然消除了图像中不均匀现象的影响, 但是对损伤区域进行了过分割, 使得本来属于损伤区域的像素被当成完好区域来处理, 大大减小了损伤的面积; 当分割阈值Th=150时, 分割结果与基于GA-Otsu方法的最佳阈值(Th=156)的分割结果基本相同, 不仅保持了冲击损伤的基本形状, 而且对冲击点位置的分割提取也较为准确。从上述分割结果的对比中可知, 本文提出的GA-Otsu方法能够对热波图像中的冲击损伤进行准确的分割提取, 为后续损伤的定量识别提供了条件。

为了进一步验证GA-Otsu法对热波检测图像分割的有效性, 对分割后的缺陷进行了定量识别, 结果如表1所示。

由表1可知, 分割误差在10%以内, 分割效果较好, 图像中缺陷的定量识别结果要小于缺陷的实际大小。总体来说, 采用GA-Otsu法对热波检测图像中的缺陷进行分割提取可以取得较好的效果。

表1

Table 1

表1(Table 1)

表1 定量识别结果 Table 1 Quantitative identification results 识别结果/mm 实际尺寸/mm 相对误差/% 缺陷一(大) 33.29 30.1 7.98 缺陷二(中) 22.10 20.2 8.47 缺陷三(小) 5.87 5.31 9.28

表1 定量识别结果 Table 1 Quantitative identification results

针对Otsu法在使用过程中存在的计算量大、效率低的问题, 将遗传算法引入到Otsu法最佳分割阈值的求解过程中, 通过优化加快了最优阈值的寻优速度, 提高了图像的分割效率。通过与人工阈值法的分割结果进行对比, 结果表明:本文方法不仅保持了冲击损伤的基本形状, 而且对冲击点位置的分割提取也较为准确。利用链码技术实现了对损伤边界的链码表示, 采用FC8技术实现了对损伤大小的定量识别。