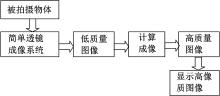
传统的成像光学系统结构一般都比较复杂, 简单透镜成像技术的目的是利用简单光学系统来代替复杂的光学系统(见图1), 同时能够获得与复杂光学系统相媲美的成像质量。根据赛德尔像差理论^[10]可知, 简单透镜成像系统要获得高质量图像所面临的主要挑战是像差。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 简单透镜计算成像替代复杂光学镜头Fig.1 Simple lenses computational imaging instead of complex optical system

如上所述, 图像去模糊的过程就是一个去卷积的过程。首先, 通过对镜头点扩散函数进行分层、分区域的提取, 采用去卷积算法可以有效去除单色像差, 消除离焦模糊达到增加光学系统景深的作用。其次, 通过对多通道的PSF进行处理还能消透镜除材料色散特性给图像带来的色差, 从而降低图像质量对镜头的依赖^[11]。简单透镜成像技术的基本过程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 简单透镜计算成像过程Fig.2 Process of simple lenses computational imaging

简单透镜成像技术的核心是计算成像, 即利用图像复原技术重建出高质量图像。图像复原技术是指利用退化现象的某种先验知识重建被退化的图像, 并最终达到改善给定图像质量的目的。因而, 图像复原重建技术就是将图像退化过程模型化, 并采用一个逆过程进行处理, 以便复原出原始的清晰度较好的高质量图像。

图像的退化模型通常近似为线性、空间不变系统, 当图像退化不是很严重的情况下, 应用线性不变系统复原图像会有比较好的效果, 同时可以降低计算复杂度并缩短复原时间。简单透镜计算成像过程可以被模型化为一个退化函数再加上一定的噪声。对一幅输入图像f(x, y)进行处理, 产生一幅退化图像g(x, y), 图像的退化模型如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 简单透镜成像观测模型Fig.3 Observation model of simple lenses computational imaging

此过程可以表达为如下形式:

gx, y=fx, yPSF+nx, y(1)

式中:g(x, y)为光学系统获得的模糊图像; f(x, y)为源图像; PSF为光学系统对应的点扩散函数; n为成像过程中引入的噪声。

PSF包含了单色像差以及色差的信息, 单透镜计算成像就是在去除噪音n(x, y), 已知g(x, y)和PSF的基础上采用去卷积的方法矫正像差, 复原出图像f(x, y)。噪音可以表示为:

nx, y=gx, y-fx, yPSF2

在噪音未知的情况下, 希望找到一个f(x, y)使得f(x, y)VPSF近似于g(x, y), 因此去卷积的过程转化为一个无约束的优化问题:

mingx, y-fx, yPSF(3)

此时, f(x, y)的解可以表达成如下形式:

f(x, y)=PSF-1(PSFT)-1PSFTgx, y(4)

为了使用更多的先验信息, 常常附加约束条件来提高图像复原精度, 令L为f(x, y)的线性算子, 复原问题可以转化为函数‖ Lf(x, y))‖ 服从式(5)约束条件的最小值问题:

‖g(x, y)-f(x, y)PSF‖2=nx, y25

再运用拉格朗日算子求解式(6):

min‖Lf(x, y)‖2+λ‖g(x, y)-f(x, y)PSF‖2=n(x, y)2]（6）

此解最终可以表达成如下形式:

f(x, y)=(PSF-1PSF+LTL/λ)-1PSFTgx, y(7)

对于图像退化较严重的非线性系统, 其PSF具有空间变化的特性, 本文利用分块复原的思想处理空间变化的模糊情况, 将模糊图像分为m× n块, 每一个子图像块再分别利用相应的PSF进行图像复原, 采用式(7)对各子图像块进行复原重建。这一过程对于整幅模糊图像而言PSF是空间变化的, 对于每个子图像块而言PSF是空间不变的^[12]。

CODEV光学设计软件仿真成像符合简单透镜成像的退化过程, 仿真图像是通过原图像与点扩散函数卷积得到的。图4为SVPSF的特征。在计算SVPSF时, 将图像划分为11× 11的网格, 但图像最外一圈只有半个网格, 计算得到的PSF也是不完整的, 需要对其进行预处理。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 空间变化点扩散函数特征Fig.4 Features of space-variant point spread function

对于PSF预处理方法, 本文首先对不完整的点扩散函数信息进行判断; 然后将其去掉并只保留中间9× 9完整的PSF, 将这81个PSF存储到集合{h_i}中, h_i表示第i个图像块的PSF, 每一个h_i都是一个小的矩阵数组, 且它的尺寸大小(行和列)为奇数, 这样可以保证它只有一个中心点。该方法适合于验证去卷积算法的有效性, 而实际系统的PSF由于受镜头加工、装调等因素的影响, 需采用实验测量的方法获取精确SVPSF。

线扩散函数(Line spread function, LSF)和调制传递函数(Modulation transfer function, MTF)都是评价光学系统成像质量的重要参数。PSF、LSF和MTF存在一定的数学关系, 若已知LSF和MTF, 通过数学方法可计算得到PSF, 如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 PSF、LSF、MTF三者之间的关系Fig.5 Relationship among PSF, LSF and MTF

根据如上所述PSF、LSF和MTF三者之间的关系, 测量PSF的具体步骤如下:

(1)通过PSF测量仪获得线扩散函数曲线。

(2)对LSF进行傅里叶变换得到一维MTF。

(3)对一维MTF进行矢量运算获得二维MTF。

(4)对二维MTF运行傅里叶逆变换获得PSF。

要计算PSF首先需测量系统的LSF, 光学传递函数测量仪采用数字傅里叶分析法可以测量不同视场的LSF和MTF。若已知光学系统的焦距f₀, 探测器对角线的一半长度为h, 那么即可取得光学系统的半视场角为:

θ=arctanf0h（8）

在图6中, 将探测器成像区域分为5× 5个子块, 设探测器尺寸大小为a× b; O为探测器成像中心视场点; O₁和O₂为子块成像中心视场; OA表示探测器对角线一半长度h。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 图像各子视场关系Fig.6 Relationship among each field of view

首先, 根据三角形比例关系可以得到式(9):

OO2=45OBOB=OAaa2+b2（9）

然后, 根据式(9)可以得到OO₂的长度为:

OO2=haa2+b2（10）

最后, 根据式(8)即可求得O₂视场大小, 再利用光传递函数测量仪测得O₂视场的LSF, 可以计算出O₂视场的PSF。

利用上述方法可以求出其他子图像块的PSF, 但需要频繁调节光学传递函数测量仪测量不同视场LSF和MTF。为了简化操作过程, 可以先测量几个视场的LSF和MTF计算求得PSF, 其余视场的PSF通过插值的方法计算获得。

在去卷积的过程中加入先验性约束可以有效地抵制图像边缘振铃效应和恢复图像细节^[13]。在已知模糊图像y和点扩散函数PSF的条件下, 通过去卷积的方法估计得到清晰图像x的过程在贝叶斯框架下可以表达为如下形式:

x=argmaxxPxy∝PyxPx(11)

条件概率P(x|y)∈ (0, 1), 当P(x|y)越接近于1时, 重构出来的图像就越接近原图像。在去卷积过程中, 假设噪声是高斯噪声, 其方差为η , 则最大相似度可以表示为:

P(y|x)∝exp-12η2‖x-Cfy‖2（12）

式中:C_f为n× n卷积矩阵。

为了更符合图像梯度分布, 引入梯度图像先验性约束进行描述:

Px=exp-α∇x‖λ(13)

根据式(11)(12)(13), 将贝叶斯后沿最大概率求解x转化为求解:

x=argminx‖Cfx-y‖2+w∇x‖λ14

式中:w=2α η 为权重因子; Ñ 表示取图像梯度; 等式右边第1项为误差项; 第2项‖ Ñ x‖ ^λ 为正则化项; λ 的取值不同, 对复原图像的平滑程度也不同。当λ =1时, 即为经典的全变分TV模型, 该模型能够保持更多的图像细节; 当λ =2时, 为Tikhonov正则化约束, 该约束容易导致复原结果过于平滑, 丢失过多图像细节; 当0< λ < 1时, 为hyper-Laplacian先验约束, 符合自然图像梯度分布, 能够保持尖锐的边缘信息。

稀疏先验约束条件能够带来更好的复原效果, 许多学者利用稀疏先验在图像复原过程中进行约束, 稀疏正则化的公式为^[14]:

-(|∇x|d-2∇x+∇2x|d-2∇2x(15)

式中:参数d用来控制梯度分布形状。

Levin等^[15]将参数d取为固定值0.8, 而在实际的图像复原迭代过程中, 随着图像清晰度的提高, 重构图像的方差逐渐增大, 其对数梯度分布的稀疏度会随之减小。根据图像复原过程中梯度分布的变化特点, 提出改进的稀疏先验正则化方法, 将控制图像梯度分布形状的参数d设置为变量, 即为可变参数的稀疏先验约束正则化算法, 那么改进的正则化约束项可写为:

C(x^k)=(|∇x^k|-μk∇x^k+|∇2x^k|-μk∇2x^k)（16）

式中:μ _k表示第k次迭代时控制重构图像梯度分布稀疏度的参数, 它在迭代的过程中是逐渐增加的, 并且每次迭代的增加量与当前重构图像的方差有关, 其表达式如下:

μk=μk-1+var(x^k)/t（17）

式中:var(· )为求方差的函数; t为一个常数, 取值范围一般为(250, 350)。

关于初始值μ ₀的选取, 因为稀疏分布的参数d满足的取值范围为(0, 1), 所以μ _k的取值范围为(1, 2), 由于μ _k在迭代过程中是逐步增大的, 因此通常选较小一点的值作为μ ₀的取值, 实验中一般的取值为(0.8, 1.5)。

假设函数ρ 表示稀疏分布函数, 表达形式为ρ (z)=|z|^λ , 本文中λ 是一个可变参数。式(14)可以表达成如下形式^{[16, 17]}:

‖y-Cfx‖2+w∑i, kρ(gi, k×x)（18）

稀疏先验约束选择了图像的少数像素进行求导, 而大部分像素保持常数, 这样有利于保持图像边缘, 抑制图像振铃效应。

稀疏先验约束使图像复原重建问题变成非凸问题, 可以使用迭代重加权最小二乘算法(IRLS)进行复原重建后的优化^{[18, 19]}。此外, 由于透镜的色散作用, 会导致不同波长光线在相同空间位置产生不同的PSF。对于给定3个颜色通道SVPSF的情况下, 在每个颜色通道去卷积的过程中可加入信号幅值投影算子对图像信号幅值进行约束, 表达式如下:

x* =Pg(x, y)=a, g(x, y)< ag(x, y), a≤g(x, y)≤bb, g(x, y)> b（19）

式中:a和b为幅值约束的下限和上限; P为信号幅值投影算子; g(x, y)为图像初始灰度值。

综上, 稀疏先验自适应图像复原算法流程如下所示。

Step1 输入独立RGB颜色通点扩散函数f_{{1, 2, 3}}和模糊图像y_{{1, 2, 3}}。

Step2 对单一颜色通道的模糊图像采用自适应稀疏先验分块复原法。

Step2.1 将输入的模糊图像分成m× n个大小相等、具有重叠矩形的图像块, 得到图像块集合{y_i}。

Step2.2 对不同图像块提取相应的局部空间不变PSF, 得到PSF集合{f_i}。

Step2.3 对模糊图像块y_i和相应的f_i采用稀疏先验自适应去卷积算子(18)复原清晰图像集合{x_i}。

Step2.4 利用迭代重加权最小二乘算法优化重构得到整幅高质量图像g_{{1, 2, 3}}。

Step3 加入幅值投影算子, 得到约束重构图像 x{1, 2, 3}*, 如式(19)所示。

Step4 将不同颜色通道图像进行融合, 得到最终清晰彩色图像。

为了验证简单透镜成像复原重建算法的有效性, 采用数字仿真与实际拍摄相结合的方式。实验测试操作系统为Windows 7(64位); 处理器为Intel Core i7-4790K; 内存为16 GB; 光学软件为CODEV; 算法开发软件为MATLAB R2015a。

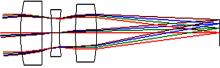
采用CODEV软件设计由三片透镜组成的简单光学系统, 技术指标如下:探测器对角线为8.59 mm; 光学系统的焦距为100 mm; F数为4.0。简单透镜成像系统二维光路如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 简单透镜成像系统光路图Fig.7 Light path of simple lenses computational imaging system

通过选取不同场景下的图像细节, 将本文算法与传统单一PSF去卷积算法进行对比, 结果如图8和图9所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 石头场景去卷积算法结果对比Fig.8 Comparison of different deconvolution algorithms in stone scene

实验结果表明, 与传统算法相比, 采用本文算法能够有效保留图像细节信息。采用峰值信噪比(PSNR)和结构自相似度(SSIM)两种客观评价方式评价图像复原质量, 结果如表1所示。

为了测试算法稳定性, 测验了20组图像, 其平均PSNR为31.3 dB, 平均SSIM为0.9587。

图9

Fig.9

	Figure Option ViewDownloadNew Window
	图9 房屋场景去卷积算法结果对比Fig.9 Comparison of different deconvolution algorithms in house scene

表1

Table 1

表1(Table 1)

表1 不同场景PSNR和SSIM结果对比 Table 1 Comparison of PSNR and SSIM in different scenes 场景 图像 PSNR SSIM 房屋 模糊图像 19.8 0.8515 传统算法 20.7 0.8809 本文方法 28.2 0.9555 石头 模糊图像 20.5 0.9089 传统算法 23.1 0.9186 本文方法 27.3 0.9612

表1 不同场景PSNR和SSIM结果对比 Table 1 Comparison of PSNR and SSIM in different scenes

此外, 采用不同数量的图像块进行图像复原, 所得到的复原结果也不一样。表2给出了采用不同数量PSF处理图像不同颜色通道的PSNR和SSIM结果。

表2

Table 2

表2(Table 2)

表2 不同分块PSNR和SSIM结果对比 Table 2 Comparison of PSNR and SSIM in different blocks PSF R G B 彩色图像 PSNR/dB SSIM PSNR/dB SSIM PSNR/dB SSIM 1 21.0 0.6175 32.9 0.9520 29.4 0.8564 20.7 0.8515 4 24.9 0.9770 32.6 0.8342 28.2 0.6504 23.5 0.8649 9 28.2 0.8304 32.7 0.9650 28.3 0.8369 25.9 0.9423 16 29.7 0.8600 33.6 0.9694 28.4 0.8302 27.0 0.9513 25 30.9 0.8812 34.1 0.9717 28.5 0.8296 28.2 0.9556 36 29.7 0.8736 32.5 0.9516 28.5 0.8291 25.2 0.9375 49 29.7 0.8761 34.3 0.9741 28.7 0.8320 27.2 0.9520

表2 不同分块PSNR和SSIM结果对比 Table 2 Comparison of PSNR and SSIM in different blocks

从表2可知:由于PSF是空间变化的, 图像块数量较少时, 在图像复原过程中估计的PSF会与真实的PSF有较大差距。而采用更多图像块进行图像去卷积复原会提高复原质量, 但重建时间过长。

图10为简单透镜成像实验测试平台。简单透镜成像系统SVPSF测量及图像复原的实验条件为:①光学传递函数测量仪; ②可见光条件下; ③30 cm长的导轨以及两个滑动底座; ④一片平凸透镜:厚度为4.2 mm、焦距为100 mm、直径为30 mm; ⑤镜头固定架:直径为30 mm, 通光孔径为25 mm; ⑥黑色的遮光绒布, 用来代替镜筒, 消除杂光影响; ⑦CMOS探测器:对角线长为8.35 mm, 像元尺寸为3.75 μ m× 3.75 μ m, 像元数为1937× 1097; ⑧计算机。

图10

Fig.10

	Figure Option ViewDownloadNew Window
	图10 简单透镜成像实验测试平台Fig.10 Test platform of simple lenses computational imaging

单透镜成像图像复原重建的具体实验方案及步骤如下所示。

Step1 利用光学传递函数测量仪测得单透镜部分视场的LSF和MTF。

Step2 通过LSF、MTF、PSF三者之间的关系, 计算得到上述各视场的PSF。

Step3 利用插值计算的方法, 获取其他视场的PSF, 最终得到单透镜成像系统空间变化的PSF。

Step4 搭建实验光路, 获取单透镜所拍摄到的模糊图像。

Step5 利用自适应稀疏先验分块去卷积算法对实验拍摄得到的模糊图像进行分块复原。

图11

Fig.11

	Figure Option ViewDownloadNew Window
	图11 实拍图像复原重建结果Fig.11 Result of image restoration and reconstruction in real condition

图12

Fig.12

	Figure Option ViewDownloadNew Window
	图12 实拍细节复原重建结果Fig.12 Details of image restoration and reconstruction through real condition

图11为实拍图像复原重建结果。由于实际拍摄的图像没有理想高分辨率图像作参考, 只能通过主观评价的方式来判断复原图像质量。图12为实拍细节复原重建结果。从图12中可以看出, 复原之后的图像细节信息更加清晰, 从而进一步验证了本文算法的有效性。