基于线性收缩的大阵列MIMO雷达目标盲检测

引用本文

姜宏, 李垠, 吕巍. 基于线性收缩的大阵列MIMO雷达目标盲检测. 吉林大学学报(工学版), 2017, 47(3): 973-980
JIANG Hong, LI Yin, LYU Wei. Linear shrinkage-based blind target detection for MIMO radar with large arrys. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 973-980 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703039
Permissions

基于线性收缩的大阵列MIMO雷达目标盲检测

姜宏, 李垠, 吕巍

吉林大学通信工程学院,长春 130012

作者简介:姜宏(1966-),女,教授,博士生导师.研究方向:阵列信号处理,信号检测与估计.E-mail:jiangh@jlu.edu.cn

基金项目:国家自然科学基金项目(61371158)

摘要

针对阵元数与快拍数可以相比拟的大阵列MIMO雷达系统,将协方差矩阵估计的收缩算法与大维随机矩阵理论相结合,提出了一种基于线性收缩-标准条件数(LS-SCN)的目标盲检测新方法。通过求解大维系统样本协方差矩阵的优化矩阵,并利用M-P律,推导了检测阈值与收缩系数之间的关系,分别给出了基于LS-SCN的单目标和多目标检测算法。该方法无需已知噪声方差、目标散射矩阵和目标方位等先验信息,对噪声变化不敏感,且适用于大阵列系统。仿真结果表明,在阵元数与快拍数在同一数量级的情况下,与SCN算法和MDL算法相比,显著提高了目标检测性能。

关键词: 通信技术; 雷达工程; 目标检测; 大维随机矩阵理论; 收缩算法; 大阵列

中图分类号:TN911.23 文献标志码:A 文章编号:1671-5497(2017)03-0973-08

Linear shrinkage-based blind target detection for MIMO radar with large arrys

JIANG Hong, LI Yin, LYU Wei

College of Communication Engineering, Jilin University, Changchun 130012, China

Abstract

Aiming at Multiple Input Multiple Output (MIMO) radar system with large arrays, in which the number of arrays is comparable to the number of snapshots, a blind target detection method based on Linear Shrinkage-Standard Condition Number (LS-SCN) is proposed by combining the shrinkage algorithm of Covariance Matrix estimation and the large dimensional random matrix theory. By solving the optimization of the sample CM in the large dimensional regime and utilizing the M-P law, the relationship between the detection threshold and the shrinkage coefficient is derived. Single-target and multi-target detection algorithms based on LS-SCN are presented respectively. The method is not sensitive to noise changes and is suitable for large array system, which do not need to know the priori information of noise variance, target scattering matrix and target location. Simulation results show that, compared with SCN algorithm and Minimum Description Length (MDL) algorithm, the proposed methods significantly improve the performance of target detection under the circumstance that the numbers of arrays and snapshots grow at the same rate.

Key words: communications; radar engineering; target detection; large-dimensional random matrix theory; shrinkage algorithm; large arrays

Show Figures

0 引言

近年来, 多输入多输出(Multiple-input multiple-output, MIMO)雷达^[1]作为一种新型雷达体制已引起广泛关注, 国内外学者在目标检测、参数估计和目标定位等领域进行了深入研究^{[2, 3]}。针对MIMO雷达系统中的目标检测问题, 学者们已提出一系列方法, 主要包括Neyman-Pearson检测^[4]、广义似然比检测^[5]、恒虚警检测^[6]、压缩感知检测^[7]及各种改进方法。这些方法多侧重于单目标检测, 虽不同程度上提高了检测性能, 但需要事先已知或预先估计噪声方差、目标散射矩阵等信息, 属于非盲检测方法。而且, 在这些MIMO雷达信号处理方法中, 为得到稳健的检测性能, 通常假定快拍数远远大于阵元数, 此时, 接收信号的样本协方差矩阵可以作为统计协方差矩阵的极大似然估计。

随着MIMO雷达技术日益走向应用, 大阵列系统^[8]已成为一种必然发展趋势。由于大阵列系统的阵元数达到几十甚至上百个, 可以与快拍数相比拟, 导致回波信号样本协方差矩阵的特征值分布区间发生改变, 传统检测与估计方法性能下降。

针对大维系统的信号处理问题, 基于收缩(Shrinkage)的协方差矩阵估计方法是近年来出现的新的信号处理手段。文献[9]研究了大维系统协方差矩阵的线性收缩估计器; 文献[10]利用Lediot-Wolf(LW)方法^[11], 针对样本数相对较少的情况, 设计了一种多目标协方差矩阵的收缩估计器; 文献[12]基于改进的LW方法, 研究了大维随机矩阵的协方差矩阵及其逆矩阵的线性收缩算法; 文献[13]研究了样本匮乏情况下噪声子空间协方差矩阵估计的收缩方法, 对传统信源数估计算法进行了改进; 文献[14]将广义收缩估计器应用于空时自适应处理(STAP)检测问题中。

近年来, 随机矩阵理论在量子物理^[15]、金融数学^[16]、无线通信^[17]等领域应用日益广泛。随着大数据时代的到来, 大维数据分析具有重要意义, 经典的统计算法难以解决数据海量化所带来的弊端, 而大维随机矩阵理论^[18]却是一种处理大维数据的有效方法, 能够为大阵列MIMO雷达系统的信号处理提供一个便利的工具。文献[19, 20]将随机矩阵理论应用于认知无线电的频谱感知问题中, 提出了盲频谱感知方法。文献[21]进一步将随机矩阵理论扩展应用于MIMO雷达目标检测领域, 提出一种多目标盲检测方法。

本文在文献[21]的基础上, 针对阵元数与快拍数可以相比拟的大阵列MIMO雷达系统, 将协方差矩阵估计的收缩算法与大维随机矩阵理论相结合, 提出了一种基于线性收缩-标准条件数(Linear shrinkage-standard condition number, LS-SCN)的目标盲检测新方法。

1 双基地MIMO雷达信号模型

假定M个发射阵元同时发射信号照射目标, 通过N个接收阵元对多次独立快拍得到的回波信号进行收集和处理, 忽略多普勒频移的影响, 在第l个快拍(l=1, …, L)期间, 回波数据可写成一个N× K维矩阵X⁽^l⁾, 即:

$\begin{matrix} X^{(l)} = \overset{P}{\sum_{p = 1}} a_{r} (φ_{p}) b_{p}^{(l)} a_{t}^{T} (θ_{p}) S + W^{(l)} \end{matrix}$ （1）

式中:S=[s₁, s₂, …, s_M]^T为发射波形矩阵, 这里s_m(m=1, 2, …, M)为第m个发射阵元所发射的波形, 其编码长度为K, 假定S为归一化正交矩阵, SS^H=I_M; 雷达区域内存在P个待检测的目标, a_r(φ _p)和a_t(θ _p)分别表示第p个目标的收、发方向矢量, $\begin{matrix} b_{p}^{(l)} \end{matrix}$ 表示第p个目标在第l个快拍期间的目标散射系数, 服从均值为0, 方差为1的高斯分布; W⁽^l⁾表示高斯白噪声矩阵。经过脉冲压缩和矢量化处理, 其输出为y⁽^l⁾=vec $\begin{matrix} (X^{(l)} S^{H}) \end{matrix}$ , 整理后可得:

$\begin{matrix} y^{(l)} = A b^{(l)} + n^{(l)} (2) \end{matrix}$

式中:n⁽^l⁾=vec $\begin{matrix} (W^{(l)} S^{H}) \end{matrix}$ 为第l个快拍期间处理后的噪声矢量; A=[a₁, a₂, …, a_P]为联合导向矩阵, 其中, a_p=a_t $\begin{matrix} (θ_{p}) \end{matrix}$ 􀱋a_r $\begin{matrix} (φ_{p}) \end{matrix}$ , p=1, 2, …, P; 􀱋表示Kronecker积; b⁽^l⁾= $\begin{matrix} {[b_{1}^{(l)}, b_{2}^{(l)}, \dots, b_{P}^{(l)}]}^{T} \end{matrix}$ 为第l个快拍期间的目标散射矢量。收集L个独立快拍期间的数据y⁽^l⁾(l=1, 2, …, L), 得到观测数据矩阵Y为:

$\begin{matrix} Y = AB + N (3) \end{matrix}$

Y= $\begin{matrix} [y^{(l)}, \dots, y^{(L)}] \end{matrix}$ , B=[b⁽^l⁾, …, b⁽^L⁾], N=[n⁽^l⁾, …, n⁽^L⁾]。

由式(3)可看出, Y是一个维数为MN× L的高斯随机矩阵。对上述模型作如下假设:

1)假设该系统为大阵列MIMO雷达系统, 即阵元数MN与快拍数L在同一数量级上;

2)假设该系统的先验信息未知, 如噪声方差未知、目标散射矩阵未知、目标位置信息未知。

2 协方差矩阵的线性收缩估计

定义R为观测数据Y的统计协方差矩阵, 即:

$\begin{matrix} R = E [Y Y^{H}] = A R_{B} A^{H} + R_{N} (4) \end{matrix}$

式中:R_B=E $\begin{matrix} [B B^{H}] \end{matrix}$ 表示目标散射信号的协方差矩阵; R_N= $\begin{matrix} σ_{n}^{2} \end{matrix}$ I_MN表示噪声的协方差矩阵; 定义 $\begin{matrix} \hat{R} \end{matrix}$ 为观测数据Y的样本协方差矩阵, 则:

$\begin{matrix} \hat{R} = \frac{1}{L} Y Y^{H} (5) \end{matrix}$

在传统信号处理方法中, 由于快拍数L远远大于MN, 通常采用 $\begin{matrix} \hat{R} \end{matrix}$ 替代R, 然而, 在大阵列MIMO雷达系统中, 由于MN与L在同一数量级, $\begin{matrix} \hat{R} \end{matrix}$ 的特征值分布区间发生变化, 将 $\begin{matrix} \hat{R} \end{matrix}$ 作为R的一致性估计的信号处理方法不再适用。本文将 $\begin{matrix} \hat{R} \end{matrix}$ 的特征值的分布区间加以收缩, 采取的方法是基于线性收缩算法对 $\begin{matrix} \hat{R} \end{matrix}$ 进行优化, 使其作为R的估计。

设R^*为Y的样本协方差矩阵 $\begin{matrix} \hat{R} \end{matrix}$ 的优化矩阵, 以R^*与R之间的均方误差最小为优化目标, 对 $\begin{matrix} \hat{R} \end{matrix}$ 进行优化, 即求解如下优化问题:

$\begin{matrix} \begin{matrix} \min_{α} E [‖ R^{*} - R ‖_{_{F}}^{^{2}}] \\ s . t . R^{*} = αF + (1 - α) \hat{R} \end{matrix} \end{matrix}$ （6）

式中:对于矩阵P∈ ℂ^{MN× MN}, ‖ P‖ _F表示P的Frobenius范数, $\begin{matrix} ‖ P ‖_{_{F}}^{^{2}} \end{matrix}$ =tr{PP^H}; α 表示收缩系数, 且α ∈ [0, 1]; F为目标矩阵^[12], 取F=tr $\begin{matrix} [\hat{R}] \end{matrix}$ /MNI_MN。本文的目的是通过最小化R^*与R之间的均方误差, 求得收缩系数的最优解α =α ₀, 从而找到R的最优估计器R^*, 方法如下:将式(6)中的均方误差代价函数表示为Q(α ), 并对其进行化简, 得到:

$\begin{matrix} \begin{matrix} Q (α) ≜ E [‖ αF + (1 - α) \hat{R} - R ‖_{_{F}}^{^{2}}] = \\ E [‖ α (F - R) + (1 - α) (\hat{R} - R) ‖_{_{F}}^{^{2}}] = \\ α^{2} ‖ F - R ‖_{_{F}}^{^{2}} + {(1 - α)}^{2} E [‖ \hat{R} - R ‖_{_{F}}^{^{2}}] + \\ 2 α (1 - α) E [tr \{Re [(F - R) {(\hat{R} - R)}^{H}]\}] \end{matrix} \end{matrix}$ （7）

在式(7)化简过程中, 利用了公式

$\begin{matrix} ‖ P + Q ‖_{_{F}}^{^{2}} = ‖ P ‖_{_{F}}^{^{2}} + ‖ Q ‖_{_{F}}^{^{2}} + 2 tr [Re (P Q^{H})], \end{matrix}$

其中, P, Q∈ ℂ^{MN× MN}, 又E $\begin{matrix} [tr \{\hat{R}\}] \end{matrix}$ =tr $\begin{matrix} \{R\} \end{matrix}$ , 因此有:E $\begin{matrix} [tr \{Re [(F - R) {(\hat{R} - R)}^{H}]\}] \end{matrix}$ =0。

令 $\begin{matrix} \frac{\partial Q (α)}{\partial α} \end{matrix}$ =0, 并考虑R和 $\begin{matrix} \hat{R} \end{matrix}$ 均为实对称阵, 经化简整理, 得到最优解α _o为:

$\begin{matrix} α_{o} = \frac{tr \{R^{2}\} - E [tr \{{\hat{R}}^{2}\}]}{\frac{1}{MN} t r^{2} \{R\} - E [tr \{{\hat{R}}^{2}\}]} \end{matrix}$ （8）

由文献[22, 23], 如果观测量服从高斯分布, 则:

$E [tr \{\hat{R}\}] = tr \{R\}$ （9）

$\begin{matrix} E [tr \{{\hat{R}}^{2}\}] = \frac{L + 1}{L} tr \{R^{2}\} + \frac{1}{L} t r^{2} \{R\} \end{matrix}$ （10）

因此, 有:

$\begin{matrix} tr \{R^{2}\} = \frac{L}{L + 1} E [tr \{{\hat{R}}^{2}\}] - \frac{1}{L + 1} {(E [tr \{\hat{R}\}])}^{2} \end{matrix}$ （11）

将式(9)(11)代入(8), 则:

$\begin{matrix} α_{o} = \frac{E [tr \{{\hat{R}}^{2}\}] + {(E [tr \{\hat{R}\}])}^{2}}{(L + 1) (E [tr \{{\hat{R}}^{2}\}] - \frac{1}{MN} {(E [tr \{\hat{R}\}])}^{2})} \end{matrix}$ （12）

假定 $\begin{matrix} \hat{R} \end{matrix}$ 的第i个特征值用ℓ_i表示, 且ℓ₁≥ ℓ₂≥ …≥ ℓ_MN, 则α _o用 $\begin{matrix} \hat{R} \end{matrix}$ 的特征值表示为:

$\begin{matrix} α_{o} = \frac{E [\overset{MN}{\sum_{i = 1}} l_{i}^{2}] + {(E [\overset{MN}{\sum_{i = 1}} l_{i}])}^{2}}{(L + 1) (E [\overset{MN}{\sum_{i = 1}} l_{i}^{2}] - \frac{1}{MN} {(E [\overset{MN}{\sum_{i = 1}} l_{i}])}^{2})} \end{matrix}$ （13）

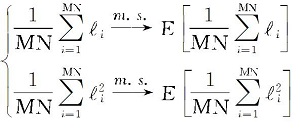
在实际中, 无法获得式(13)中E $\begin{matrix} [\overset{MN}{\sum_{i = 1}} l_{i}^{2}] \end{matrix}$ 和E $\begin{matrix} [\overset{MN}{\sum_{i = 1}} l_{i}] \end{matrix}$ 的值, 当MN→ ∞ , L→ ∞ 且MN/L→ c(c为一个正常数)的情况下, 由文献[13], 有:

其中, 表示均方收敛, 因此, 将式(14)代入式(13), 得到α _o的一致估计为:

$\begin{matrix} {\hat{α}}_{o} \end{matrix}$ = $\begin{matrix} \frac{\overset{MN}{\sum_{i = 1}} l_{i}^{2} + {(\overset{MN}{\sum_{i = 1}} l_{i})}^{2}}{(L + 1) (\overset{MN}{\sum_{i = 1}} l_{i}^{2} - \frac{1}{MN} {(\overset{MN}{\sum_{i = 1}} l_{i})}^{2})} \end{matrix}$ (15)

从而, R^*的预估计为:

$\begin{matrix} R_{o}^{*} = {\hat{α}}_{o} F + (1 - {\hat{α}}_{o}) \hat{R} \end{matrix}$ （16）

由于 $\begin{matrix} {\hat{α}}_{o} \end{matrix}$ 的值可能大于1, 定义新的收缩系数ρ =min( $\begin{matrix} {\hat{α}}_{o} \end{matrix}$ , 1), 最终得到优化矩阵R^*为:

$\begin{matrix} R^{*} = ρF + (1 - ρ) \hat{R} \end{matrix}$ （17）

其中, 令μ = $\begin{matrix} \overset{MN}{\sum_{i = 1}} \end{matrix}$ ℓ_i/MN, 则矩阵F=μ I_MN。

3 基于LS-SCN的单目标盲检测

算法

首先考虑单目标情况, 即目标数P=1。用H₀表示目标不存在的情况, H₁表示目标存在的情况, 则双基地MIMO雷达目标检测的二元假设模型为:

$\begin{matrix} \{\begin{matrix} H_{0} : Y = N \\ H_{1} : Y = AB + N \end{matrix} \end{matrix}$ （18）

式中:N表示均值为0, 协方差矩阵为 $\begin{matrix} σ_{n}^{2} \end{matrix}$ I_MN的高斯白噪声矩阵。当MN→ ¥ , L→ ¥ 且MN/L→ c(0< c< ¥ )时, 由大维随机矩阵理论和M-P律^[24], $\begin{matrix} \hat{R} \end{matrix}$ 的特征值的渐近谱分布为:

$\begin{matrix} f_{\hat{R}} (l) = {(1 - c^{- 1})}^{+} δ (l) + \frac{\sqrt[]{{(l - a)}^{+} {(b - l)}^{+}}}{2 πc l} \end{matrix}$ （19）

式中:δ $\begin{matrix} (l) \end{matrix}$ 表示单位冲激函数; ℓ为 $\begin{matrix} \hat{R} \end{matrix}$ 的特征值, ℓ∈ $\begin{matrix} [a, b] \end{matrix}$ , a和b分别为 $\begin{matrix} \hat{R} \end{matrix}$ 的最小和最大特征值的极限值, 并且:

将优化矩阵R^*的第i个特征值用λ _i表示, 且λ ₁≥ λ ₂≥ …≥ λ _MN, 由式(17), λ _i可表示为:

$\begin{matrix} λ_{i} = ρμ + (1 - ρ) l_{i} (22) \end{matrix}$

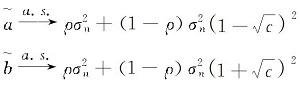
式中:i=1, 2, …, MN, λ _i∈ [ $\begin{matrix} \tilde{a} \end{matrix}$ , $\begin{matrix} \tilde{b} \end{matrix}$ ], $\begin{matrix} \tilde{a} \end{matrix}$ 和 $\begin{matrix} \tilde{b} \end{matrix}$ 分别为R^*的最小、最大特征值的极限值。当MN→ ¥ , L→ ¥ 且MN/L→ c时, μ 趋近于 $\begin{matrix} σ_{n}^{2} \end{matrix}$ , 由式(20)、(21)和(22), $\begin{matrix} \tilde{a} \end{matrix}$ 和 $\begin{matrix} \tilde{b} \end{matrix}$ 分别满足:

由式(23)、(24), 得到大阵列双基地MIMO雷达目标检测的判决阈值为:

$\begin{matrix} γ = \frac{ρ + (1 - ρ) {(1 + \sqrt[]{c})}^{2}}{ρ + (1 - ρ) {(1 - \sqrt[]{c})}^{2}} \end{matrix}$ （25）

可见, 所推导的阈值γ 与收缩系数ρ 有关。进一步, 采用标准条件数法, 设检测统计量为:

$\begin{matrix} T = \frac{λ_{1}}{λ_{MN}} \end{matrix}$ （26）

则判决规则如下:

$\begin{matrix} Decision = \{\begin{matrix} H_{0}, T \leq γ \\ H_{1}, T > γ \end{matrix} \end{matrix}$ （27）

即:将检测统计量T与判决阈值γ 相比较, 若T> γ , 则判决目标存在; 否则判决目标不存在。

4 基于LS-SCN的多目标盲检测算法

对于多目标检测问题, 假定目标数P未知, 定义 $\begin{matrix} {\hat{H}}_{0} \end{matrix}$ 为目标数检测错误的情况, $\begin{matrix} {\hat{H}}_{1} \end{matrix}$ 为目标数检测正确的情况。在单目标检测算法基础上, 提出一种基于序贯LS-SCN的多目标检测算法。

设R^*⁽^p⁾和 $\begin{matrix} {\hat{R}}^{(p)} \end{matrix}$ 分别为R^*和 $\begin{matrix} \hat{R} \end{matrix}$ 删除前p-1行和p-1列所组成的子矩阵, p=1, …, min(MN, L)-1。将R^*⁽^p⁾的特征值按降序排列为:

$\begin{matrix} λ_{p} \geq λ_{p + 1} \geq \dots \geq λ_{MN} (28) \end{matrix}$

则第p个目标的检测统计量为:

$\begin{matrix} T^{(p)} = \frac{λ_{p}}{λ_{MN}} \end{matrix}$ （29）

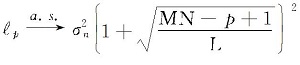
为得到判决阈值, 根据M-P律, $\begin{matrix} {\hat{R}}^{(p)} \end{matrix}$ 的最大特征值趋近于其极限值:

由式(24), 优化矩阵R^*⁽^p⁾的最大特征值趋近于其极限值, 即:

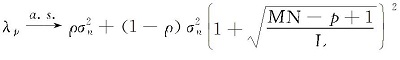
因此, 检测第p个目标的判决阈值为:

$\begin{matrix} γ^{(p)} = \frac{ρ + (1 - ρ) {(1 + \sqrt[]{(MN - p + 1) / L})}^{2}}{ρ + (1 - ρ) {(1 - \sqrt[]{MN / L})}^{2}} \end{matrix}$ （32）

其检测模型可表示为:

$\begin{matrix} T^{(p)} \overset{H_{1}}{\underset{H_{0}}{\geq}} γ^{(p)} \end{matrix}$ （33）

算法的具体实现步骤如下:

(1)假设p=1;

(2)由式(29)和式(32)分别计算检测统计量T⁽^p⁾和判决阈值γ ⁽^p⁾, 利用式(33)对第p个目标进行检测, 判决目标是否存在;

(3)如果第p个目标存在, 将p+1代替p重复步骤(2), 否则, 进入下一步;

(4)确定检测目标数为 $\begin{matrix} \hat{P} \end{matrix}$ =p-1, 即:

$\begin{matrix} \hat{P} = \underset{p}{\arg \max} \{\frac{λ_{p}}{λ_{MN}} > γ^{(p)}\} \end{matrix}$ （34）

式中:p=1, …, min(MN, L)-1。

判决规则为:

$\begin{matrix} Decision = \{\begin{matrix} {\hat{H}}_{0}, \hat{P} \neq P \\ {\hat{H}}_{1}, \hat{P} = P \end{matrix} \end{matrix}$ （35）

这样, 多目标检测概率可表示为:

$\begin{matrix} P_{d} = Prob \{num (\hat{P} = P) / N_{t}\} \end{matrix}$ （36）

式中:N_t为蒙特拉罗实验次数。

5 仿真结果与分析

为了验证本文所提出方法的有效性, 利用MATLAB进行仿真, 并与传统方法的检测性能进行对比。假定P(H_i; H_j)表示在H_j情况下出现H_i的概率, 则目标的检测概率为P_d=P(H₁; H₁), 虚警率为P_fa=P(H₁; H₀), 正确判决概率为P_c= $\begin{matrix} \frac{P (H_{1}; H_{1}) + P (H_{0}; H_{0})}{2} \end{matrix}$ 。

设MIMO雷达的收发阵列为均匀线阵构成的大阵列, 其发射和接收阵元数分别为M=12, N=12, 快拍数L=150(此时MN与L在同一数量级, 其比值c=MN/L=24/25)。发射波形编码长度为K=128, 采用1000次蒙特拉罗仿真实验分别对单目标和多目标检测算法进行验证。

5.1 单目标检测的仿真结果

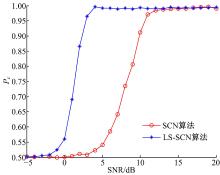
设目标数P=1, 其发射角与到达角为(40° , 10° ), 虚警率P_fa为0.015, 将本文的LS-SCN算法与SCN算法的正确判决概率P_c进行了对比, 得到P_c与信噪比SNR之间的关系曲线如图1所示。

	Figure Option View Download New Window
	图1 正确判决概率与信噪比的关系Fig.1 The probability of correct decision versus SNR

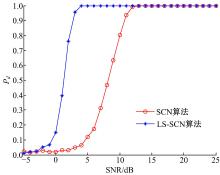
仿真结果表明:在相同信噪比条件下, 本文LS-SCN算法的正确判决概率高于SCN算法。SCN算法将γ ₀=b/a作为判决阈值, 在大阵列MIMO雷达系统下, 由于快拍数相对匮乏导致其性能下降。而本文LS-SCN算法的判决阈值γ = $\begin{matrix} \tilde{b} \end{matrix}$ / $\begin{matrix} \tilde{a} \end{matrix}$ 与收缩系数ρ 有关, 通过收缩作用可以改变最大最小特征值的极值范围, 因此将其作为大阵列系统的检测门限更合理有效。尤其是在低信噪比时, 所提出的LS-SCN算法的正确判决概率更高, 检测性能更好。

进一步, 将LS-SCN算法与SCN算法的检测概率P_d进行比较, 图2所示为两种算法的单目标检测概率与信噪比之间的关系曲线。

	Figure Option View Download New Window
	图2 单目标检测概率与信噪比的关系Fig.2 The probability of detection versus SNR for single target detection

仿真结果表明:两种算法的检测概率都随着信噪比的增加而增大, 本文LS-SCN算法优于SCN算法。而且, 在低信噪比时LS-SCN算法具有较好的检测性能, 弥补了传统方法不适用于大阵列MIMO雷达系统的缺陷, 提高了目标检测的稳健性。

当信噪比为10 dB时, 固定MN, 改变快拍数L, 得到收缩系数ρ 随L变化的曲线如图3所示。

	Figure Option View Download New Window
	图3 收缩系数与快拍数的关系Fig.3 The shrinkage coefficient versus the number of snapshots

图3的仿真结果表明:当阵元数MN一定时, 收缩系数ρ 随着快拍数L的增大而变小。当L远大于MN时, ρ 变得很小, 可以忽略不计, 此时相当于采用传统信号处理方法, 即:用样本协方差矩阵作为统计协方差矩阵的估计; 然而, 当L变小、接近于MN时, ρ 变大, 对样本协方差矩阵特征值的收缩作用变得明显, 此时, 采用优化后的矩阵作为统计协方差矩阵的估计是非常必要的。可见, LS-SCN算法更适用于阵元数与快拍数相接近的大阵列MIMO雷达系统。

5.2 多目标检测的仿真结果

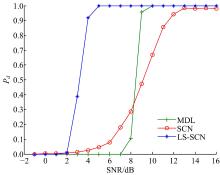
假定目标数P=3, 其发射角与到达角分别为(60° , 40° ), (10° , 30° ), (20° , 50° ), 虚警率P_fa仍设为0.015, 将所提出的LS-SCN算法与SCN算法、MDL算法进行了比较, 这3种算法的多目标检测概率与信噪比之间的关系如图4所示。

	Figure Option View Download New Window
	图4 多目标检测概率与信噪比的关系Fig.4 The probability of detection versus SNR for multi-target detection

	Figure Option View Download New Window
	图5 不同目标数时检测概率与信噪比的关系Fig.5 The probability of detection versus SNR for different number of targets

	Figure Option View Download New Window
	图6 不同快拍数时检测概率与信噪比的关系Fig.6 The probability of detection versus SNR for different number of snapshots

仿真结果表明, LS-SCN算法的多目标检测性能始终优于SCN算法和MDL算法, 尤其在低信噪比环境下, LS-SCN算法的检测性能优势更明显。

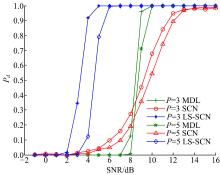
进一步, 分别考虑目标数为3和5的情况, 以及快拍数为150和600的情况, 图5为不同目标数情况下检测概率与信噪比之间的关系曲线, 图6为不同快拍数情况下检测概率与信噪比之间的关系曲线。对比不同目标数的仿真可看出, 目标数的大小对于检测性能有一定的影响, 目标增多时检测性能略有下降, 但LS-SCN算法始终优于SCN算法和MDL算法。对比不同快拍数的仿真可看出, 在快拍数较大情况下, SCN算法性能略逊于LS-SCN算法, 但差别不大; 在快拍数匮乏情况下, SCN算法的性能严重下降, 而LS-SCN算法仍保持优越的检测性能。

6 结束语

在大阵列MIMO雷达系统中, 用样本协方差矩阵替代统计协方差矩阵的信号处理手段不再适用, 为解决这一问题, 本文提出一种基于LS-SCN的大阵列MIMO雷达目标检测方法, 对单目标检测和多目标检测问题分别进行了研究, 推导了判决阈值与收缩系数之间的关系。该方法无需已知噪声方差、目标散射矩阵和目标位置等先验信息。另外, 为获得良好的检测性能, 传统算法必须要求快拍数远远大于阵元数, 而本文方法的快拍数与阵元数可以在同一数量级, 从而解决了在快拍数相对于阵元数不足情况下目标检测性能严重下降的问题。仿真结果表明, 与SCN算法和MDL算法相比, 所提出的LS-SCN算法在大阵列MIMO雷达系统中具有更好的检测性能, 在快拍数匮乏情况下显著提高了大阵列系统目标检测的稳健性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Fishler E, Haimovich A, Blum R, et al. MIMO radar: an idea whose time has come[C]//Proc IEEE Radar Conference, Philadelphia, Pennsylvania, USA, 2004: 71-78. [本文引用:1]
[2]	陈浩文, 黎湘, 庄钊文. 一种新型的雷达体制-MIMO雷达[J]. 电子学报, 2012, 40(6): 1190-1198. Chen Hao-wen, Li Xiang, Zhuang Zhao-wen. A rising radar system-MIMO radar[J]. Acta Electronica Sinica, 2012, 40(6): 1190-1198. [本文引用:1]
[3]	肖文书. MIMO雷达中的信号检测[J]. 电子学报, 2010, 38(3): 626-631. Xiao Wen-shu. Model of signal detection for MIMO radar[J]. Acta Electronica Sinica, 2010, 38(3): 626-631. [本文引用:1]
[4]	Ding J, Chen H W, Wang H, et al. Low-grazing angle target detection and system configuration of MIMO radar[J]. Progress in Electromagnetics Research B, 2013, 48: 23-42. [本文引用:1]
[5]	关键, 黄勇. MIMO雷达多目标检测前跟踪算法研究[J]. 电子学报, 2010, 38(6): 1449-1453. Guan Jian, Huang Yong. Track-before-detect algorithm in a MIMO radar multi-target environment[J]. Acta Electronica Sinica, 2010, 38(6): 1449-1453. [本文引用:1]
[6]	Wang P, Li H, Himed B. A parametric moving target detector for distributed MIMO radar in non-homogeneous environment[J]. IEEE Transactions on Signal Processing, 2013, 61(9): 2282-2294. [本文引用:1]
[7]	Anitor L, Maleki A, Otten M, et al. Design and analysis of compressed sensing radar detectors[J]. IEEE Transactions on Signal Processing, 2013, 61(4): 813-827. [本文引用:1]
[8]	Rusek F, Persson D, Lau B K, et al. Scaling up MIMO: opportunities and challenges with large arrays[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40-60. [本文引用:1]
[9]	Couillet R, Pascal F, Silverstein J W. Robust estimates of covariance matrices in the large dimensional regime[J]. IEEE Transaction on Information Theory, 2014, 60(11): 7269-7278. [本文引用:1]
[10]	Lancewicki T, Aladjem M. Multi-target shrinkage estimation for covariance matrices[J]. IEEE Transactions on Signal Processing, 2014, 62(24): 6380-6390. [本文引用:1]
[11]	Ledoit O, Wolf M. A well-conditioned estimator for large-dimensional covariance matrices[J]. J Multivar Anal, 2004, 88(2): 365-411. [本文引用:1]
[12]	Walden A T, Schneider-Luftman D. Rand om matrix derived shrinkage of spectral precision matrices[J]. IEEE Transactions on Signal Processing, 2015, 63(17): 4689-4699. [本文引用:1]
[13]	Huang L, So H C. Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix[J]. IEEE Transactions on Signal Processing, 2013, 61(19): 4806-4821. [本文引用:1]
[14]	Pascal F, Chitour Y, Quek Y. Generalized robust shrinkage estimator and its application to STAP detection problem[J]. IEEE Transactions on Signal Processing, 2014, 62(21): 5640-5651. [本文引用:1]
[15]	Guhr T, Groeling A M, Weidenmuller H. Rand om matrix theories in quantum physics: common concepts[J]. Physics Reports, 1998, 299(4): 189-425. [本文引用:1]
[16]	Bouchaud J P, Potters M. Theory of Financial Risks-from Statistical Physics to Risk Management[M]. Cambridge: Cambridge University Press, 2000. [本文引用:1]
[17]	Bai Z D, Fang Z B, Liang Y C. Spectral Theory of Large Dimensional Rand om Matrices and Its applications to Wireless Communications and Fiance Statistics[M]. Hefei: University of Science and Technology of China Press, 2009: 1-20. [本文引用:1]
[18]	Bai Z D, Jack W Silverstein. Spectral Analysis of Large Dimensional Rand om Matrices[M]. 2nd ed. Beijing: Science Press, 2010. [本文引用:1]
[19]	王磊, 郑宝玉, 李雷. 基于随机矩阵理论的协作频谱感知[J]. 电子与信息学报, 2009, 31(8): 1925-1929. Wang Lei, Zheng Bao-yu, Li Lei. Cooperative spectrum sensing based on rand om matrix theory[J]. Journal of Electronics & Information Technology, 2009, 31(8): 1925-1929. [本文引用:1]
[20]	Chatzinotas S, Sharma S K, Ottersten B. Asymptotic analysis of eigenvalue-based blind Spectrum Sensing techniques[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, Canada, 2013: 4464-4468. [本文引用:1]
[21]	Jiang H, Tang X, Lyu W, et al. Blind multi-target detection for bistatic MIMO radar based on rand om matrix theory[C]//The 3rd IEEE China Summit & International Conference on Signal Information Processing (ChinaSIP2015), Chengdu, China, 2015: 1047-1051. [本文引用:1]
[22]	Chen Y, Wiesel A, Eldar Y C, et al. Shrinkage algorithms for MMSE covariance estimation[J]. IEEE Transactions on Signal Processing, 2010, 58(10): 5016-5029. [本文引用:1]
[23]	兰星, 李伟, 颜佳冰, 等. 部分发射天线损毁时MIMO雷达信号认知优化[J]. 重庆邮电大学学报: 自然科学版, 2016, 28(2): 168-173. Lan Xing, Li Wei, Yan Jia-bing, et al. Cognitive optimization for MIMO radar signal with part of transmitting antennas damaged[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2016, 28(2): 168-173. [本文引用:1]
[24]	Couillet R, Debbah M. Rand om Matrix Methods for Wireless Communications[M]. Cambridge: Cambridge University Press, 2011. [本文引用:1]

2004

0.0

... 0 引言近年来,多输入多输出(Multiple-input multiple-output,MIMO)雷达^[1]作为一种新型雷达体制已引起广泛关注,国内外学者在目标检测、参数估计和目标定位等领域进行了深入研究^[2,3] ...

2012

0.0

2010

0.0

2013

0.0

... 针对MIMO雷达系统中的目标检测问题,学者们已提出一系列方法,主要包括Neyman-Pearson检测^[4]、广义似然比检测^[5]、恒虚警检测^[6]、压缩感知检测^[7]及各种改进方法 ...

2010

0.0

2013

0.0

2013

0.0

2013

0.0

... 随着MIMO雷达技术日益走向应用,大阵列系统^[8]已成为一种必然发展趋势 ...

2014

0.0

2014

0.0

2004

0.0

... 文献[10]利用Lediot-Wolf(LW)方法^[11],针对样本数相对较少的情况,设计了一种多目标协方差矩阵的收缩估计器 ...

2015

0.0

... F为目标矩阵^[12],取F=tr R^/MNI_MN ...

2013

0.0

2014

0.0

1998

0.0

... 近年来,随机矩阵理论在量子物理^[15]、金融数学^[16]、无线通信^[17]等领域应用日益广泛 ...

2000

0.0

... 近年来,随机矩阵理论在量子物理^[15]、金融数学^[16]、无线通信^[17]等领域应用日益广泛 ...

2009

0.0

... 近年来,随机矩阵理论在量子物理^[15]、金融数学^[16]、无线通信^[17]等领域应用日益广泛 ...

2010

0.0

... 随着大数据时代的到来,大维数据分析具有重要意义,经典的统计算法难以解决数据海量化所带来的弊端,而大维随机矩阵理论^[18]却是一种处理大维数据的有效方法,能够为大阵列MIMO雷达系统的信号处理提供一个便利的工具 ...

2009

0.0

2013

0.0

2015

0.0

2010

0.0

2016

0.0

2011

0.0

... )时,由大维随机矩阵理论和M-P律^[24], R^的特征值的渐近谱分布为: ...