符号干扰多径信道下可达信道容量的预编码方案

引用本文

韩伟良, 葛建华, 马波, 高洋. 符号干扰多径信道下可达信道容量的预编码方案. 吉林大学学报(工学版), 2017, 47(3): 981-987
HAN Wei-liang, GE Jian-hua, MA Bo, GAO Yang. Precoding design to achieve capacity bound in inter-symbol-interference fading channels. Journal of Jilin University Engineering and Technology Edition, 2017, 47(3): 981-987 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201703040
Permissions

符号干扰多径信道下可达信道容量的预编码方案

韩伟良, 葛建华, 马波, 高洋

西安电子科技大学 ISN国家重点实验室,西安 710071

葛建华(1961-),男,教授,博士生导师.研究方向:宽带无线通信,数字电视传输.E-mail:jhge@xidian.edu.cn

作者简介:韩伟良(1984-),男,博士研究生.研究方向:宽带无线通信,预编码.E-mail:hanweiliang1205@126.com

基金项目:“973”国家重点基础研究发展计划项目(2012CB316100); 高等学校学科创新引智计划项目(B08038); 中国博士后科学基金项目(2015M580816); 国家自然科学基金项目(61501347)

摘要

提出了一种基于发射端已知信道状态信息(CSIT)的预编码方案,使发送和接收两端仅进行一次预编码和一次均衡运算就能获得多径满分集增益和逼近高斯理想信道的瞬时容量。首先,根据采用最小均方误差(MMSE)均衡的单载波频域均衡(SC-FDE)系统收发两端的互信息,给出一个收发互信息的理论上界。然后,发射端在已知CSIT条件下给出可达互信息理论上界的预编码方案,并且通过理论分析给出可达上界的预编码方案中断概率性能的闭合表达式。仿真结果表明:该方案能够有效改善系统的中断概率性能,在瑞利ISI信道下,能够将单纯采用MMSE均衡的SC-FDE系统的中断概率所需信噪比降低2~3 dB。同时,该方案所能达到的瞬时信道容量逼近于高斯信道下MMSE均衡系统的容量。

关键词: 通信技术; 单载波频域均衡; 最小均方误差均衡; 预编码

中图分类号:TN929.53 文献标志码:A 文章编号:1671-5497(2017)03-0981-07

Precoding design to achieve capacity bound in inter-symbol-interference fading channels

HAN Wei-liang, GE Jian-hua, MA Bo, GAO Yang

State Key Laboratory of Integrated Service Networks, Xidian University, Xi'an, 710071, China

Abstract

A novel precoding scheme is proposed with perfect Channel State Information at Transmitter (CSIT), which only takes one precoding and one Minimum Mean Square Error (MMSE) equalization at the transmitter and the receiver, respectively. Thus, the full diversity gain is obtained and the instant channel capacity approaches to the performance of Single-Carrier Frequency Domain Equalization (SC-FDE) in Gaussian channel. First, a theoretical mutual information bound between the transmitter and the receiver is presented based on the SC-FDE system with MMSE receiver. The, the precoding scheme is designed to achieve this bound. Through theoretical analysis, a closed-form expression on the outage probability of the system is derived. Simulation results demonstrate that the proposed scheme can reduce the outage probability of the traditional MMSE system by 2~3 dB and the instant channel capacity approaches to the performance of SC-FDE in Gaussian channel.

Key words: communication technology; single carrier frequency domain equalization (SC-FDE); minumum mean square error (MMSE); precoding

Show Figures

0 引言

单载波频域均衡(Single carrier frequency domain equalization, SC-FDE)系统, 由于其发送结构简单, 能够很好地抵抗多径衰落, 是下一代无线通信系统中重要的上行链路解决方案。近年来, 为了提升SC-FDE的系统性能, 研究人员分别从接收端和发送端两个方面提出了改进方案。一方面, 从接收端入手, 通过采用复杂的迭代均衡和解调达到最优的中断概率及误码率性能。在单用户系统中, 单载波系统通过自适应反馈信道估计(Decision feedback channel estimation, DFCE), 首先要获得准确的估计和反馈信道, 为信道均衡提供理想的条件^[1]。获得准确的信道状态信息(Channel state information, CSI)以后, 采用Turbo均衡方法^[2]或者IB-DFE方法^[3], 通过反复迭代来减小信道估计误差和噪声带来的影响, 最终至少能够在衰落信道中提升系统性能3~5 dB, 并且获得更高的分集增益, 但是IB-DFE以及MMSE Turbo方法的复杂度随发送块长的增长呈几何增长, 不太适合大型系统使用。于是文献[4, 5]结合迭代块反馈均衡(Iterative block decision feedback equalization, IB-DFE)方法和基站协作方法, 通过频率的重用、LDPC编码和接收端Turbo均衡, 改善了比特错误概率性能。文献[6, 7]提出了一种在多输入、多输出信道(Multiple input multiple output, MIMO)中通过最小化加权均方误差的和获得MIMO干扰信道下具有线性约束的最优均衡方法。但是该方案需要在发射端有用户进行协作, 增加了接收端的信道估计和信道系数反馈带来的负担。在MIMO系统接收端, 根据发送信号的协方差构造了具有线性约束的最优化发送接收方案, 把原来的问题转化为一个具有功率约束的半定规划问题(Semidefinite program, SDP), 最后利用优化方法求得最优解^[8]。但是优化算法的计算时间不可预测, 不能够保证在规定时间内完成解调。这些方案都是通过提升接收系统的解调复杂度来换取性能, 给解调带来了巨大负担。于是文献[9]提出了一种次优的迭代均衡解码方案, 通过次优的滤波器系数迭代获得复杂度和性能的平衡。另外一方面, 从发送端入手, 通过预编码来配合接收端改善系统性能。文献[10]利用频域的Tomlinson-Harashima技术进行发送端的预编码处理, 在降低系统复杂度的同时有效地降低了多用户系统检测的误码率性能, 但是对于单发、单收的单用户系统, 却不能获得理想的效果。文献[11]则将接收机的负担全部转到了发射机上, 针对超宽带系统中的扩频方案, 提出了两种预编码方案, 一种是把接收端的瑞克(Rake)接收机搬到发送端, 提出了一种预先进行Rake合并的方案; 第二种是基于迫零均衡的预均衡方案。文献[11]将所有的计算负担都转换给发送端, 同时达到了注水法均衡下的信道容量, 但是第一种方案需要扩频支持才能实现, 而第二种方案则在时域进行预均衡, 会引起拖尾和均衡剩余误差, 因此提出了取L个最强多径的简化算法。简化算法虽然解决了计算复杂度的问题, 却带来了高信噪比下错误平层的问题。

本文提出了一种基于发送端和接收端联合设计的预编码方案, 当发送端已知CSI时, 在频域进行预编码, 在接收端, 采用在频域MMSE均衡的方案。整个系统无需迭代计算和优化算法即可获得多径满分集增益及逼近信道容量的性能, 还能够有效避免文献[11]在时域中的滤波器均衡带来的拖尾、均衡剩余误差以及错误平层的问题。

1 系统模型

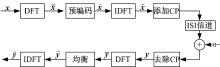
如图1所示, 考虑一个单输入、单输出(Single input single output, SISO)的SC-FDE系统, 发射端原始的信息序列为:

$\begin{matrix} x = {[x (0), x (1), \dots, x (N - 1)]}^{T} (1) \end{matrix}$

	Figure Option View Download New Window
	图1 预编码MMSE SC-FDE系统框图Fig.1 Diagram of precoding MMSE SC-FDE system

假设发送端已知完整的CSIT, 即h= $\begin{matrix} {[h (0), \dots, h (D - 1)]}^{T} \end{matrix}$ , 为了方便分析, 本文在此信道冲击响应后面补零至长度N。于是得到h= $\begin{matrix} {[h (0), \dots, h (D - 1), 0, \dots, 0]}^{T} \end{matrix}$ 。首先, 对发送端的信息序列x进行DFT变换, 可以得到:

$\begin{matrix} \bar{x} = {[\bar{x} (0), \bar{x} (1), \dots, \bar{x} (N - 1)]}^{T} (2) \end{matrix}$

式中: $\begin{matrix} \bar{x} \end{matrix}$ =Ux, U为DFT矩阵。

针对频域的信息序列, 左乘预编码对角矩阵C, 得到 $\begin{matrix} \tilde{x} \end{matrix}$ = $\begin{matrix} \bar{Cx} \end{matrix}$ , C=diag{c₀, c₁, …, c_N-₁}为发送端的预编码对角矩阵。再对此向量 $\begin{matrix} \tilde{x} \end{matrix}$ 进行IDFT变换, 得到待发送的信息序列 $\begin{matrix} \hat{x} \end{matrix}$ = $\begin{matrix} \tilde{Ux} \end{matrix}$ 。最后, 在序列 $\begin{matrix} \hat{x} \end{matrix}$ 前端添加循环前缀(Cyclic prefix, CP), 通过天线将信息序列发送至接收端。

接收端在收到信息序列以后, 首先将序列的CP去除。由于CP的存在, 得到的信息序列y=[y $\begin{matrix} (0) \end{matrix}$ , y $\begin{matrix} (1) \end{matrix}$ , …, y $\begin{matrix} (N - 1) \end{matrix}$ ]^T可以表示为发送序列 $\begin{matrix} \hat{x} \end{matrix}$ 和信道冲击响应h的循环卷积, 即:

$\begin{matrix} y (n) = \overset{N - 1}{\sum_{d = 0}} h (d) x (< n - d >_{N}) + η (n) (3) \end{matrix}$

式中:< · > _N是将该数据进行模除N的操作; η $\begin{matrix} (n) \end{matrix}$ 是均值为零, 方差为1的噪声序列。

然后利用DFT矩阵U将y变换至频域, 得到 $\begin{matrix} \bar{y} \end{matrix}$ =Uy。利用已经估计得到的频域等价信道系数矩阵对所得到的 $\begin{matrix} \bar{y} \end{matrix}$ 进行均衡, 得到 $\begin{matrix} \tilde{y} \end{matrix}$ = $\begin{matrix} \bar{Wy} \end{matrix}$ , W为均衡矩阵。最后, 对 $\begin{matrix} \tilde{y} \end{matrix}$ 进行IDFT变换, 得到时域估计的信息序列 $\begin{matrix} \hat{y} \end{matrix}$ =U^H $\begin{matrix} \tilde{y} \end{matrix}$ , 即可对该序列进行逐符号的判决。

根据MMSE准测^[12], 均衡以后获得的数据向量为:

$\begin{matrix} \hat{y} = \sqrt[]{ρ} U^{H} {[Λ^{H} Λ + ρ^{- 1} I]}^{- 1} Λ^{H} U H_{eq} U^{H} CUx + U^{H} {[Λ^{H} Λ + ρ^{- 1} I]}^{- 1} Λ^{H} Uη \end{matrix}$ (4)

式中:η 为时域的噪声向量; H_eq为等效的时域Toepelitz信道矩阵, 它的第一列即为h。

根据式(4)可以得到等价的噪声向量为:

$\begin{matrix} \hat{n} \end{matrix}$ = $\begin{matrix} \hat{y} \end{matrix}$ - $\begin{matrix} \sqrt[]{ρ} \end{matrix}$ x= $\begin{matrix} \sqrt[]{ρ} \end{matrix} \begin{matrix} (U^{H} {[Λ^{H} Λ + ρ^{- 1} I]}^{- 1} Λ^{H} U H_{eq} U^{H} CU - I) \end{matrix}$ x+U^H $\begin{matrix} {[Λ^{H} Λ + ρ^{- 1} I]}^{- 1} \end{matrix}$ Λ ^HUH_eqU^HCUη (5)

由于U为酉矩阵, 于是噪声的自协方差可以表示为 $\begin{matrix} \hat{R} \end{matrix}$ E $\begin{matrix} [\hat{n} {\hat{n}}^{H}] \end{matrix}$ 。对 $\begin{matrix} \hat{R} \end{matrix}$ 求偏导, 可以得到W= $\begin{matrix} {[Λ^{H} Λ + ρ^{- 1} I]}^{- 1} \end{matrix}$ Λ ^H。因此, 检测信息序列所获得的信号干扰噪声比(Signal to interference plus noise ratio, SINR)为:

$\begin{matrix} \begin{matrix} γ_{n}^{MMSE} ≜ \frac{ρ}{\hat{R} (n, n)} - 1 = \\ ρ {(\frac{1}{N} tr [\hat{R}])}^{- 1} - 1 = \\ ρ {(\frac{1}{N} tr {[ρ Λ^{H} Λ + I]}^{- 1})}^{- 1} - 1 = \\ {[\frac{1}{N} \overset{N - 1}{\sum_{k = 0}} \frac{1}{1 + ρ {|λ_{k} c_{k}|}^{2}}]}^{- 1} - 1 \end{matrix} \end{matrix}$ (6)

于是, 估计信号 $\begin{matrix} \hat{y} \end{matrix}$ 和原始信号x的互信息可以表示为:

$\begin{matrix} I_{MMSE} (x; \hat{y}) = \frac{1}{N} \overset{N - 1}{\sum_{n = 0}} \log (1 + γ_{n}^{MMSE}) = - \log [\frac{1}{N} \overset{N - 1}{\sum_{k = 0}} \frac{1}{1 + ρ {|λ_{k} c_{k}|}^{2}}] \end{matrix}$ （7）

最后, 由式(7)可以得到互信息I_MMSE $\begin{matrix} (x; \hat{y}) \end{matrix}$ 小于数据速率R的中断概率为:

$\begin{matrix} P_{out} = P \{\frac{1}{N} \overset{N - 1}{\sum_{k = 0}} \frac{1}{1 + ρ {|λ_{k} c_{k}|}^{2}} > 2^{- R}\} \end{matrix}$ （8）

2 预编码设计

根据互信息的表达式(7)给出该系统能够获得的互信息的理论上界, 然后根据该理论上界给出可达互信息理论上界的预编码方案。首先, 有以下命题:

命题1 互信息I_MMSE $\begin{matrix} (x; \hat{y}) \end{matrix}$ 具有理论上界, 当且仅当 $\begin{matrix} {|λ_{i} c_{i}|}^{2} \end{matrix}$ = $\begin{matrix} {|λ_{j} c_{j}|}^{2} \end{matrix}$ , i, j∈ $\begin{matrix} [0, N - 1] \end{matrix}$ , i≠ j时, 能够达到理论上界:

$\begin{matrix} I_{MMSE} (x; \hat{y}) \leq - \log [1 / (1 + \frac{ρ}{N} \overset{N - 1}{\sum_{k = 0}} {|λ_{k}|}^{2})] = - \log [1 / (1 + \frac{ρ P_{tot}}{N})] \end{matrix}$ (9)

式中:P_tot= $\begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} {|λ_{k}|}^{2} \end{matrix}$ = $\begin{matrix} \overset{D - 1}{\sum_{d = 0}} \end{matrix} \begin{matrix} {|h (d)|}^{2} \end{matrix}$ 为信道的总功率。

证明考虑 $\begin{matrix} \frac{1}{N} \end{matrix} \begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} \frac{1}{1 + ρ {|λ_{k} c_{k}|}^{2}} \end{matrix}$ , 其中c_k为预编码矩阵对角线上的第k个系数。根据代数平均数和调和平均数的不等式可以得到:

$\begin{matrix} \frac{1}{\frac{1}{N} \overset{N - 1}{\sum_{k = 0}} \frac{1}{1 + ρ {|λ_{k} c_{k}|}^{2}}} \leq \frac{\overset{N - 1}{\sum_{k = 0}} (1 + ρ {|λ_{k} c_{k}|}^{2})}{N} \end{matrix}$ (10)

当且仅当 $\begin{matrix} {|λ_{i} c_{i}|}^{2} \end{matrix}$ = $\begin{matrix} {|λ_{j} c_{j}|}^{2} \end{matrix}$ , i, j∈ $\begin{matrix} [0, N - 1] \end{matrix}$ , i≠ j时, 不等式(10)成立。由于预编码矩阵不能改变信道总功率, 即 $\begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} {|λ_{k} c_{k}|}^{2} \end{matrix}$ = $\begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} {|λ_{k}|}^{2} \end{matrix} \begin{matrix} {|c_{k}|}^{2} \end{matrix}$ = $\begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} {|λ_{k}|}^{2} \end{matrix}$ , 根据帕塞瓦尔定理, $\begin{matrix} \overset{N - 1}{\sum_{k = 0}} \end{matrix} \begin{matrix} {|λ_{k}|}^{2} \end{matrix}$ = $\begin{matrix} \overset{D - 1}{\sum_{d = 0}} \end{matrix} \begin{matrix} {|h (d)|}^{2} \end{matrix}$ =P_tot。所以, 式(10)的右边可以重新写为:

$\begin{matrix} \frac{\overset{N - 1}{\sum_{k = 0}} (1 + ρ {|λ_{k} c_{k}|}^{2})}{N} = 1 + \frac{ρ P_{tot}}{N} \end{matrix}$ (11)

于是, 互信息I_MMSE $\begin{matrix} (x; \hat{y}) \end{matrix}$ 的理论上界可以写为:

$\begin{matrix} I_{MMSE} (x; \hat{y}) \leq - \log (\frac{1}{\frac{1}{N} \overset{N - 1}{\sum_{k = 0}} (1 + ρ {|λ_{k} c_{k}|}^{2})}) = - \log (\frac{1}{1 + \frac{ρ P_{tot}}{N}}) \end{matrix}$ (12)

反之, 当不等式(12)成立时, 不等式(10)使得条件 $\begin{matrix} {|λ_{i} c_{i}|}^{2} \end{matrix}$ = $\begin{matrix} {|λ_{j} c_{j}|}^{2} \end{matrix}$ , i, j∈ $\begin{matrix} [0, N - 1] \end{matrix}$ , i≠ j必然成立。

证毕。

根据命题1的证明可以知道, 预编码矩阵的系数c_k应该满足以下两个条件:

$\overset{N - 1}{\sum_{k = 0}} {|λ_{k} c_{k}|}^{2} = \overset{N - 1}{\sum_{k = 0}} {|λ_{k}|}^{2} = P_{tot}$ (13)

$\begin{matrix} \begin{matrix} {|λ_{i} c_{i}|}^{2} = {|λ_{j} c_{j}|}^{2} \\ i, j \in [0, N - 1], i \neq j \end{matrix} \end{matrix}$ (14)

于是, 可以通过简单的解方程的方法获得系数c_k为:

$\begin{matrix} {|c_{k}|}^{2} = \frac{\overset{N - 1}{\sum_{k = 0}} {|λ_{k}|}^{2}}{N {|λ_{k}|}^{2}} = \frac{P_{tot}}{N {|λ_{k}|}^{2}} \end{matrix}$ （15）

然后, 得到系统的预编码矩阵为:

$\begin{matrix} C = diag \{c_{0}, c_{1}, \dots, c_{N - 1}\} (16) \end{matrix}$

于是系统的中断概率可以重新写为:

$\begin{matrix} P_{out} = P \{\frac{1}{1 + \frac{ρ P_{tot}}{N}} > 2^{- R}\} \end{matrix}$ （17）

3 性能分析

根据式(17), 假设 $\begin{matrix} \overset{D - 1}{\sum_{d = 0}} \end{matrix} \begin{matrix} {|h (d)|}^{2} \end{matrix}$ =P_tot, 其中, 每个抽头系数h $\begin{matrix} (d) \end{matrix}$ 都是服从均值为零、方差为 $\begin{matrix} σ_{n}^{2} \end{matrix}$ 的复高斯分布。由式(17)可以得到:

$\begin{matrix} P \{\overset{D - 1}{\sum_{d = 0}} {|h (d)|}^{2} < \frac{N}{ρ} (2^{R} - 1)\} = \int_{x}^{=} f_{X} (x) dx \end{matrix}$ (18)

式中:f_X $\begin{matrix} (x) \end{matrix}$ 为 $\begin{matrix} \overset{D - 1}{\sum_{d = 0}} \end{matrix} \begin{matrix} {|h (d)|}^{2} \end{matrix}$ 的联合概率密度函数, 其中每一个 $\begin{matrix} {|h (d)|}^{2} \end{matrix}$ 均服从参数n=2的卡方分布, 令y= $\begin{matrix} {|h (d)|}^{2} \end{matrix}$ , 其概率密度函数为:

$\begin{matrix} f_{Y} (y) = \{\begin{matrix} \frac{1}{2} \exp (- \frac{y}{2 P_{tot} / D}), y > 0 \\ 0, 其他 \end{matrix} \end{matrix}$

要获得x= $\begin{matrix} \overset{D - 1}{\sum_{d = 0}} \end{matrix} \begin{matrix} {|h (d)|}^{2} \end{matrix}$ 的概率密度函数, 需要将 $\begin{matrix} {|h (d)|}^{2} \end{matrix}$ 的概率密度函数进行卷积。这样的计算过程比较复杂, 参考文献[13]中的方法, 首先获得 $\begin{matrix} {|h (d)|}^{2} \end{matrix}$ 概率密度函数的拉普拉斯变换为:

$\begin{matrix} L \{\frac{1}{2} \exp (- \frac{y}{2 P_{tot} / D})\} = \frac{1}{\frac{1}{P_{tot} / D} + 2 s} \end{matrix}$ (19)

时域的卷积等价于拉普拉斯域的相乘^[14], 于是得到 $\begin{matrix} \overset{D - 1}{\sum_{d = 0}} \end{matrix} \begin{matrix} {|h (d)|}^{2} \end{matrix}$ 的概率密度函数的拉普拉斯变换为:

$\begin{matrix} L \{\overset{D - 1}{\sum_{d = 0}} {|h (d)|}^{2}\} = 1 / {(\frac{1}{P_{tot} / D} + 2 s)}^{D} \end{matrix}$ (20)

对式(20)进行拉普拉斯逆变换, 得到式(18)中的f_X(x)的概率密度函数为:

$\begin{matrix} P (f_{X} (x)) = \frac{x^{D - 1}}{2^{D} Γ (D) {(P_{tot} / D)}^{D - 1}} \exp (- \frac{x}{2 P_{tot} / D}) \end{matrix}$ (21)

则系统的中断概率可以由式(21)积分得到, 即:

$\begin{matrix} \begin{matrix} \int_{x}^{=} f_{X} (x) dx = \\ \int_{x}^{=} \frac{x^{D - 1}}{2^{D} Γ (D) {(P_{tot} / D)}^{D - 1}} \exp (- \frac{x}{2 P_{tot} / D}) dx = \\ \frac{1}{Γ (D)} \int_{z}^{=} z^{D - 1} \exp (- z) dz = \\ Υ (D, \frac{ND}{2 ρ P_{tot}} (2^{R} - 1)) \end{matrix} \end{matrix}$ (22)

式中:其中Υ (· )是不完全伽玛函数。这里, 有效分集增益定义为^[15]:

$\begin{matrix} d_{e} = \frac{\ln P_{out}}{lnρ} \end{matrix}$ （23）

当ρ → ¥ 时, d_out= $\begin{matrix} \lim_{ρ \to \infty} \end{matrix}$ d_e, 即:

$\begin{matrix} \lim_{ρ \to \infty} \{lnΥ (D, \frac{ND}{2 ρ P_{tot}} (2^{R} - 1))] / \ln (ρ)\} \end{matrix}$

可以得到系统的分集阶数增益为:

$\begin{matrix} d_{out} = D (24) \end{matrix}$

根据式(24)可以知道, 系统可以获得多径满分集增益。

4 仿真分析

将本文方案与未采用预编码的MMSE均衡方案与文献[3]中采用IB-DFE的方案进行了比较。同时, 将本文方案的瞬时信道容量与采用理论公式(22)计算的信道容量公式进行了比较, 另外给出了高斯信道下采用MMSE均衡的信道容量, 以此证明本文方案的可靠性以及理论分析的准确性。

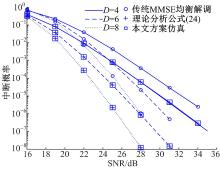
将本文方案与传统的采用MMSE均衡的SC-FDE系统进行了中断概率的仿真分析, 结果如图2所示。仿真条件为N=32, R=1。从图2可以看出, 当D=4时, 相比原有MMSE方案, 本文方案可以有效提升系统增益2 dB; 当D=6, 8时, 本文方案相比原来MMSE方案提升的性能超过2 dB。同时, 从图2可以看出, 采用理论公式(24)计算的中断概率与实际的仿真曲线很好地重合了。

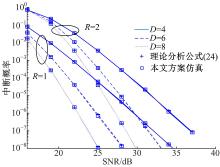
将本文方案在不同数据速率R下的中断概率进行仿真分析, 结果如图3所示。仿真条件为N=16。从图3可以看出, 当D=4时, R=1与R=2的曲线组完全平行了, 即它们在高信噪比条件下取得了相同的分集增益。在ISI信道长度D=6和D=8时, 也有相同的结论, 说明本文方案取得了很好的多径满分集增益。具体分集增益如图4所示。从图3还可以看出, 系统的中断概率受数据速率的影响。随着数据速率的增加, 系统的分集增益降低, 对应于图中中断概率的曲线随着R的增大而向右平移。

	Figure Option View Download New Window
	图2 传统MMSE与本文方案的中断概率比较Fig.2 Outage comparison of tradition MMSE and proposed scheme

	Figure Option View Download New Window
	图3 本文方案在不同数据速率R下中断概率的比较Fig.3 Outage comparison of proposed scheme at different data rate R

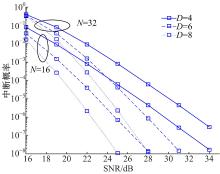
将本文方案在不同的数据块长下的中断概率进行仿真分析, 结果如图4所示。仿真参数为R=1。从图4中可以看出, 不同的数据块长会取得相同的多径满分集增益, 即分集增益的阶数不受具体块长的影响。但是数据块越长, 系统会损失越多的编码增益, 即中断概率曲线随着N的增大向右平移了。

图5中将本文方案的有效分集增益式(24)进行了比较。从图5可以看出, 在信噪比较低时, 增加数据速率或者数据块长, 系统有效分集增益都会减小。对应于图中有效分集增益的曲线, 随着R或者N的增大曲线右移。但是随着系统信噪比的提升,

	Figure Option View Download New Window
	图4 本文方案在不同块长N下中断概率的比较Fig.4 Outage comparison of proposed scheme at different block size N

	Figure Option View Download New Window
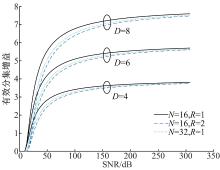	图5 本文方案理论公式的有效分集增益仿真Fig.5 Effective diversity simulation for theoretic expression of proposed scheme

系统最终的分集增益不受R或者N的影响, 即图中具有相同的ISI信道长度曲线在高信噪比的趋势都是相同的。从图5还可以看出, 本文方案在高信噪比时, 获得了多径满分集增益。

图6将本文方案的信道容量与MMSE均衡方案所达到的信道容量进行了比较, 同时给出了SC-FDE系统在高斯信道下的容量。这里的容量采用香农给出的容量计算公式C=log(1+γ ), 其中γ 是通过式(6)计算获得的SINR。从图6可以看出, 本文方案能够在ISI衰落信道下很好地逼近高斯信道的容量极限, 同时比单纯采用MMSE均衡方案的容量有很大提升。

图7将本文方案的误码率性能与文献[3]中使用IBDFE反馈迭代均衡方案的

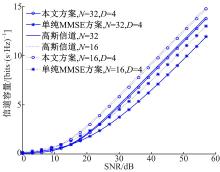	Figure Option View Download New Window
	图6 本文方案与单纯MMSE均衡方案所达到的信道容量比较Fig.6 Comparison of channel capacity of proposed scheme and tradition MMSE equalization scheme

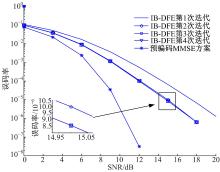	Figure Option View Download New Window
	图7 本文方案与迭代MMSE均衡方案的误码率性能比较Fig.7 Bit error rate comparison of proposed scheme and iterative MMSE equalization scheme

误码率性能进行了比较。仿真参数为N=16, D=4。由图7可以看出, 相比于单纯MMSE均衡方案, 本文方案能够获得多径满分集增益, 同时, 可以使系统的误码率性能提升4~5 dB左右。而发射端仅采用了简单的预编码方案, 接收端的方案未进行改变。

5 结束语

提出了一种在SC-FDE系统中采用MMSE均衡方案的新型预编码方案, 该方案在发送端已知信道状态信息的条件下, 达到了逼近系统信道容量的性能, 同时有效地将解调负担分散至发送端和接收端, 减轻了单纯在接收端解调的复杂度。最后, 通过理论分析以及仿真试验验证了本文所提的方案的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Mihara H, Maehara F. Decision feedback channel estimation scheme using terminal speed for single-carrier frequency-domain equalization[C]//IEEE 81st Vehicular Technology Conference, Glasgow, Scotland , UK, 2015: 1-5. [本文引用:1]
[2]	Laot C, Le Bidan R, Leroux D. Low-complexity MMSE turbo equalization: a possible solution for EDGE[J]. IEEE Transactions on Wireless Communications, 2005, 4(3): 965-974. [本文引用:1]
[3]	Ribeiro F C, Dinis R, Cercas F, et al. On the theoretical BER performance of SC-FDE schemes with IB-DFE receivers[C]//IEEE 81st Vehicular Technology Conference, Glasgow, Scotland , UK, 2015: 6-10. [本文引用:1]
[4]	Gante J, Gomes M, Dinis R, et al. Towards an enhanced frequency reuse: Base station cooperation with turbo frequency domain receivers[C]//IEEE International Conference on Communications, London, 2015: 2786-2790. [本文引用:1]
[5]	Gante J, Gomes M, Dinis R, et al. Clustered multiuser detection using SC-FDE transmission with iterative receivers[C]//IEEE 81st Vehicular Technology Conference, Glasgow, Scotland , UK, 2015: 21-25. [本文引用:1]
[6]	Kaviani S, Simeone O, Krzymień W, et al. Linear MMSE precoding and equalization for network MIMO with partial cooperation[C]//IEEE Global Telecommunications Conference, Houston, TX, USA, 2011: 1-6. [本文引用:1]
[7]	肖寒春, 蒋文科, 张祖凡. 分层动态虚拟 MIMO 的信道容量分析[J]. 重庆邮电大学学报: 自然科学版, 2015, 27(2): 174-178. Xiao Han-chun, Jiang Wen-ke, Zhang Zu-fan. Channel capacity analysis of hierarchical dynamic virtual MIMO[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2015, 27(2): 174-178. [本文引用:1]
[8]	Weng C C, Vaidyanathan P P. MIMO transceiver optimization with linear constraints on transmitted signal covariance components[J]. IEEE Transactions on Signal Processing, 2010, 58(1): 458-462. [本文引用:1]
[9]	Ravinder O, Raju M, Ramakrishna M, et al. Sub-optimal joint equalization and decoding approach for SC-FDE[C]//IEEE International Conference on Electrical, Electronics, Signals, Communication and Optimization, Visakhapatnam, India, 2015: 1-6. [本文引用:1]
[10]	Hwang J K, Wang W F, Li J D. Low-complexity frequency-domain Tomlinson-Harashima precoding for low-PAPR SC-LFDMA system[C]//IEEE 13th International Conference on Communication Technology, Ji'nan, China, 2011: 171-176. [本文引用:1]
[11]	Ding G, Wang D, Chen Z. Performance evaluation of two kinds of precoding joint with MMSE equalization in DS-UWB[C]//IEEE First International Conference on Communications and Networking in China, Beijing, China, 2006: 1-5. [本文引用:1]
[12]	Tajer A, Nosratinia A. Diversity order in ISI channels with single-carrier frequency-domain equalizers[J]. IEEE Transactions on Wireless Communications, 2010, 9(3): 1022-1032. [本文引用:1]
[13]	Wang Hai-ming, You Xiao-hu, Jiang Bin, et al. Performance analysis of frequency domain equalization in SC-FDMA systems[C]//IEEE International Conference on Communications, Beijing, China, 2008: 4342-4347. [本文引用:1]
[14]	Oppenheim A V, Schafer R W, Buck J R. Discrete-Time Signal Processing[M]. Englewood Cliffs: Prentice-hall, 1989: 254-284. [本文引用:1]
[15]	Uysal M. Maximum achievable diversity order for cascaded rayleigh fading channels[J]. Electronics Letters, 2005, 41(23): 1289-1290. [本文引用:1]

2015

0.0

... 在单用户系统中,单载波系统通过自适应反馈信道估计(Decision feedback channel estimation,DFCE),首先要获得准确的估计和反馈信道,为信道均衡提供理想的条件^[1] ...

2005

0.0

... 获得准确的信道状态信息(Channel state information,CSI)以后,采用Turbo均衡方法^[2]或者IB-DFE方法^[3],通过反复迭代来减小信道估计误差和噪声带来的影响,最终至少能够在衰落信道中提升系统性能3~5 dB,并且获得更高的分集增益,但是IB-DFE以及MMSE Turbo方法的复杂度随发送块长的增长呈几何增长,不太适合大型系统使用 ...

2015

0.0

2015

0.0

2015

0.0

2011

0.0

2015

0.0

. 2015, 27(2):174-178 DOI:doi:10.3979/j.issn.1673-825X.2015.02.006

Channel capacity analysis of hierarchical dynamic virtual MIMO

分层动态虚拟 MIMO 的信道容量分析

Xiao Han-chun , Jiang Wen-ke , Zhang Zu-fan.

肖寒春, 蒋文科, 张祖凡

针对如何解决目前移动通信频率紧缺及信道容量不足的问题,提出了一种新型的分层动态虚拟多输入多输出(multiple input multiple output,MIMO)系统结构,该结构结合了移动云的灵活接入、覆盖面积广等特点,并将虚拟MIMO技术融合在该结构中,较显著地提高了系统的信道容量。在该结构下,用户在层次之间进行通信并利用注水算法进行功率的优化分配。而对用户在跨越多层次进行通信的情形,提出了一种同时将层次间距离和传输功率进行最优化的马尔可夫链算法。该算法通过监测用户的变化进而调节层次间距离和传输功率,从而获得最大的信道容量。仿真结果显示,注水算法通过功率优化获得了层次间的分层动态虚拟MIMO结构的最大信道容量,马尔可夫链算法实现了用户跨越多层次通信情形下的最大信道容量。

2010

0.0

... 在MIMO系统接收端,根据发送信号的协方差构造了具有线性约束的最优化发送接收方案,把原来的问题转化为一个具有功率约束的半定规划问题(Semidefinite program,SDP),最后利用优化方法求得最优解^[8] ...

2015

0.0

2011

0.0

2006

0.0

2010

0.0

... 根据MMSE准测^[12],均衡以后获得的数据向量为: ...

2008

0.0

1989

0.0

... 时域的卷积等价于拉普拉斯域的相乘^[14],于是得到 ∑d=0D-1hd2的概率密度函数的拉普拉斯变换为: ...

2005

0.0

... 这里,有效分集增益定义为^[15]: ...